Solar Wind Turbulence and the Role of Ion Instabilities

Abstract

Solar wind is probably the best laboratory to study turbulence in astrophysical plasmas. In addition to the presence of magnetic field, the differences with neutral fluid isotropic turbulence are: (i) weakness of collisional dissipation and (ii) presence of several characteristic space and time scales. In this paper we discuss observational properties of solar wind turbulence in a large range from the MHD to the electron scales. At MHD scales, within the inertial range, turbulence cascade of magnetic fluctuations develops mostly in the plane perpendicular to the mean field, with the Kolmogorov scaling $k_{\perp}^{-5/3}$ for the perpendicular cascade and $k_{\|}^{-2}$ for the parallel one. Solar wind turbulence is compressible in nature: density fluctuations at MHD scales have the Kolmogorov spectrum. Velocity fluctuations do not follow magnetic field ones: their spectrum is a power-law with a −3/2 spectral index. Probability distribution functions of different plasma parameters are not Gaussian, indicating presence of intermittency. At the moment there is no global model taking into account all these observed properties of the inertial range. At ion scales, turbulent spectra have a break, compressibility increases and the density fluctuation spectrum has a local flattening. Around ion scales, magnetic spectra are variable and ion instabilities occur as a function of the local plasma parameters. Between ion and electron scales, a small scale turbulent cascade seems to be established. It is characterized by a well defined power-law spectrum in magnetic and density fluctuations with a spectral index close to −2.8. Approaching electron scales, the fluctuations are no more self-similar: an exponential cut-off is usually observed (for time intervals without quasi-parallel whistlers) indicating an onset of dissipation. The small scale inertial range between ion and electron scales and the electron dissipation range can be together described by $\sim k_{\perp}^{-\alpha}\exp(-k_{\perp}\ell_{d})$, with α≃8/3 and the dissipation scale ℓ _d close to the electron Larmor radius ℓ _d ≃ρ _e . The nature of this small scale cascade and a possible dissipation mechanism are still under debate.

1 Introduction

Natural plasmas are frequently in a turbulent state characterized by large, irregular fluctuations of the physical parameters. The spatial and temporal scales of these fluctuations cover a large range, usually extending down to the smallest scales resolved by the observations. Well known examples are provided by the solar wind, the magnetosheath of planetary magnetospheres, the interstellar medium, etc.

Is there a certain degree of generality in the physics of the various astrophysical situations where turbulent states are observed? If this is the case, is it of the same nature as what happens in incompressible neutral (or magnetized) fluid turbulence, which is a non-linear process, non-reproducible locally but with some “universal” statistical properties? These “universal” statistical properties are thought to result from the combination of (1) an infinite number of degrees of freedom, each characterized by its spatial and temporal scale; (2) the absence of characteristic spatial and temporal scales, which implies some sort of equivalence between all of the degrees of freedom; (3) a nonlinear transfer of energy between these degrees of freedom, often called a cascade of energy.

To be more specific, the incompressible fluid turbulence occurs at large Reynolds numbers Re=LV _L /η≫1 (where L is the scale at which the energy is injected in the system, that is of the order of the correlation length of the largest turbulent eddy, V _L the typical value of velocity fluctuations at scale L and η the kinematic viscosity). This is verified when the energy injection scale is sufficiently far from the dissipation scale ℓ _d (L≫ℓ _d ). Thanks to a number of observations, numerical simulations and theoretical works, the following universal properties of a turbulent system have been firmly established:

• In Fourier space, at intermediate scales $L^{-1} \ll k\ll\ell _{d}^{-1}$ (k being a wave-number), within the so called inertial range, the power spectrum of the velocity fluctuations is observed to follow a k ^−5/3 law, independently of how the energy is injected in the system, and of how it is dissipated at small scales. A power-law spectrum suggests scale invariance, i.e., at each scale the same physical description is valid (the Navier-Stokes equation for fluids and the magnetohydrodymanic equations for magnetized plasmas are scale invariant and describe well self-similar turbulent fluctuations).

• Intermittency, due to spatial nonuniformity of the energy transfer across scales, manifests itself as a scale dependent departure from Gaussian distributions of the probability distribution functions of the turbulent fluctuations.

To date, 3D fluid turbulence is far from being understood, and there is no satisfactory theory, based on first principles, that fully describes it in a sufficiently general frame. Therefore one has to rely on “phenomenologies” which attempt to provide a framework for the interpretation of experimental results; for example the empirical k ^−5/3 law is well described by the Kolmogorov’s phenomenology (hereafter K41) (Kolmogorov 1941a; Frisch 1995). In this simple model of turbulence, kinetic energy E _c is supposed to cascade from large scales to small scales and the cascade rate (an energy per unit time) is constant over the inertial range ε=∂E _c /∂t=const. Since the only timescale that appears in the system is the time of the energy exchange between the fluctuations (the eddies), also called the non-linear or eddy turnover time τ _nl =ℓ/δv, the cascade rate can be approximated by ε≈(δv)²/τ _nl =const. It follows that the velocity field fluctuations δv≈(εℓ)^1/3 so that the power spectrum (δv)²/k goes like ℓ ^5/3 or k ^−5/3.

Intermittency is beyond the Kolmogorov phenomenology but it has been observed that in neutral fluids it appears in the form of coherent structures as filaments of vorticity. Their characteristic length can be of the order of the energy injection scale L but their cross-section is of the order of the dissipation scale ℓ _d (see the references of Sect. 8.9 in Frisch 1995). Thus, in Fourier space, these filaments occupy all scales including the edges of the inertial range.

As we have said, in the phenomenological framework of turbulence, the majority of the results are based on the interpretation of experimental results. However, one important theoretical result was obtained from the Navier-Stokes equation, independently of K41 phenomenology: it is known as Kolmogorov’s 4/5 law (hereafter K4/5). The K4/5 law prescribes that, for fully developed incompressible turbulence in a stationary state¹, under conditions of isotropy, local homogeneity, and vanishing dissipation (i.e., in the inertial range), the third order moment of the longitudinal (i.e. along the bulk flow) velocity fluctuations δv scales linearly with the separation ℓ (or with the time scale τ=ℓ/V, with V being a bulk flow speed):

$$ Y(\ell)=\bigl\langle\delta v^3 \bigr\rangle= -4/5 \varepsilon\ell, $$

(1)

the proportionality factor ε being the mean energy transfer rate and dissipation rate of the turbulent cascade (see Frisch 1995, Sect. 6.2, and references therein). This law has been indeed observed in the neutral fluid turbulence, e.g. Danaila et al. (2001). Note that Kolmogorov 4/5 law can be obtained from the more general Yaglom (1949) law in case of Navier-Stokes isotropic turbulence.

When the energy cascade “arrives” to the spatial (or time) scale of the order of the dissipation scale ℓ _d , the spectrum becomes curved (Grant et al. 1962), indicating a lack of self-similarity. This spectrum is also universal (see, e.g., Fig. 8.14 in Frisch 1995) and can be described by ∼k ³exp(−ckℓ _d ) with c≃7 (Chen et al. 1993). In neutral fluids the dissipation sets in usually at scales of the order of the collisional mean free path.

We shall restrict ourselves here to the solar wind turbulence, which is perhaps our best laboratory for studying astrophysical plasma turbulence (Tu and Marsch 1995; Bruno and Carbone 2005; Horbury et al. 2005; Matthaeus and Velli 2011). Does the solar wind turbulence share the above universal characteristics, such as power-law spectra, intermittency and linear dependence between the third order moment of the fluctuations and the energy transfer rate? How does the dissipation set in? and is its spectrum universal?

The solar wind expands radially but not with spherical symmetry. Fast, rather steady wind at around 700 km/s flows from coronal holes, generally at high solar latitudes. More variable slow wind (200–500 km/s) is thought to have its source around coronal hole boundaries or in transiently open regions. In general, the properties of fluctuations within fast and slow wind at 1 AU are rather different, with fast wind turbulence appearing less developed than that in slow wind, indicating different “age of turbulence”. Interactions between fast and slow wind, as well as transient events, produce compressions, rarefactions and shocks. When considering the innate properties of plasma turbulence, it is usually easier to treat steady, statistically homogeneous intervals of data from individual streams.

In situ spacecraft measurements in the solar wind provide time series of local plasma parameters. Therefore, in Fourier space, we have a direct access to frequency spectra. When the flow speed of the solar wind V _sw is much larger than the characteristic plasma speeds, one can invoke the Taylor’s hypothesis (Taylor 1938; Perri and Balogh 2010) and convert a spacecraft-frame frequency f to a flow-parallel wavenumber k in the plasma frame $k=\frac{2 \pi f}{V_{sw}}$. At scales larger than the proton characteristic scales, we can largely treat the solar wind fluctuations using magnetohydrodynamics (MHD) (Marsch and Mangeney 1987; Biskamp 1993; Schekochihin et al. 2009). The flow speed V _sw is typically much larger than the Alfvén speed $V_{A}=B/\sqrt{4\pi\rho }\simeq50$ km/s (B being the magnetic field and ρ the mass density) and far faster than spacecraft motions, so that one can use Taylor’s hypothesis. At plasma kinetic scales, the Taylor hypothesis can be used in the absence of quasi-parallel propagating whistler waves, which have a phase speed higher than V _sw .

The solar wind is pervaded with fluctuations on all measured scales. These fluctuations form energy spectra following power laws as expected for developed turbulence. For example, for magnetic fluctuations, at very large scales (for the spacecraft-frame frequencies f<10⁻⁴ Hz) the power spectrum goes as ∼f ⁻¹. This spectrum can be interpreted in terms of uncorrelated large scale Alfvén waves (Matthaeus and Goldstein 1986; Horbury et al. 2005). A recent work proposes that it originates due to the nonlinear coupling in the corona between outgoing and ingoing Alfvén waves with the help of multiple reflections on the non-homogeneous transition region (Verdini et al. 2012). The corresponding frequency range is usually called the energy injection scales (Bruno and Carbone 2005). The maximal frequency f ₀ of this range, or outer scale of the turbulent cascade, is close to 10⁻⁴ Hz at 1 AU. It was proposed by Mangeney et al. (1991), Salem (2000), Meyer-Vernet (2007), that at the outer scale there is a balance between the solar wind expansion time τ _exp =R/V _sw at a radial distance R and the eddy-turnover time τ _nl ; and the turbulent cascade can develop at scales where τ _nl <τ _exp . Estimations at 1 AU for V _sw =600 km/s give τ _exp ≃70 h. The characteristic non-linear time at f ₀ is of the order of τ _nl ≃70 h as well². At smaller scales, i.e. at higher frequencies f>10⁻⁴ Hz, the non-linear time becomes smaller than the expansion time and turbulent cascade develops. As τ _exp increases with R, the outer scale increases, i.e. f ₀ shifts towards lower frequencies. This is indeed observed in the solar wind (Bruno and Carbone 2005). It will be interesting to verify the relationship between the outer-scale and τ _exp with solar wind observations for different turbulence levels and at different heliospheric distances.

Within the ∼[10⁻⁴,10⁻¹] Hz range, magnetic spectrum is usually observed to follow the K41 scaling, interpreted as the inertial range (the details on the spectral slope of the inertial range will be discussed in Sect. 2). The spectrum undergoes new changes at the proton characteristic scales (appearing in the measured spectra at ∼[0.1,1] Hz) and at the electron scales ∼[50,100] Hz (see details in Sect. 3).

One of the important differences of the solar wind turbulence with the isotropic neutral fluid turbulence is the presence of the mean magnetic field ${\bf B}$, which introduces a privileged direction and so imposes an anisotropy of turbulent fluctuations. In the inertial range, the observed magnetic fluctuations δB _∥ along the mean field are usually much smaller than the transverse Alfvénic fluctuations δB _⊥. The wave vector distributions are not isotropic either, k _⊥>k _∥. In Sect. 2 we will discuss in more details how this k-anisotropy has been detected within the inertial range of the solar wind turbulence and its possible interpretations. We will discuss as well intermittency in the solar wind and show recent verification of the K4/5 law.

Another important difference between neutral fluid turbulence and solar wind turbulence is the weakness of collisional dissipation in the solar wind, as for most of the space plasmas. The dissipation process at work and the dissipation length are not known precisely. There are observational indications and theoretical considerations that characteristic plasma scales may be good candidates to replace, in some sense, the dissipation scale of fluid turbulent cascade. The characteristic plasma scales are the ion Larmor radius $\rho_{i}=\sqrt {2k_{B}T_{i\perp}/m_{i}}/(2\pi f_{ci})$ (with k _B being the Boltzmann’s constant, T _i⊥ being the ion temperature perpendicular to the magnetic field ${\bf B}$, m _i being the ion mass), the ion inertia length λ _i =c/ω _pi (with c the speed of light and ω _pi the ion plasma frequency), the corresponding electron scales ρ _e ,λ _e , and the ion and electron cyclotron frequencies f _ci,e =qB/(2πm _i,e ) (with q being the charge of the particle). At these scales different kinetic effects may take place. However, the precise mechanism (or mechanisms) which dissipates electromagnetic turbulent energy in the solar wind and the corresponding spatial and/or temporal scale(s) are still under debate. The details of the observations of solar wind turbulence around plasma kinetic scales will be discussed in Sect. 3. In particular, in Sect. 3.2 we discuss the ion temperature anisotropy instabilities which may control turbulent fluctuations around ion scales. Conclusions are found in Sect. 4.

2 The MHD Scale Cascade

An MHD theory of cascading turbulence similar to Kolmogorov, but carried by Alfvénic fluctuations propagating in the large-scale magnetic field ${\bf B}$ was proposed independently by Iroshnikov (1963) and Kraichnan (1965) (IK hereafter). In this model, the fluctuations are still assumed to be isotropic but most of the energy transfer is due to interactions between Alfvénic fluctuations moving in opposite direction along ${\bf B}$ with the Alfvén speed V _A . This limits the time during which two eddies interact, which is of the order of an Alfvén time τ _A ∼ℓ/V _A . It is also assumed that the interactions are weak such that τ _A ≪τ _nl , and thus a number of interactions proportional to τ _nl /τ _A is needed to transfer the energy (Dobrowolny et al. 1980). Following the argument of Kolmogorov and under the assumption of equipartition between magnetic and kinetic energies, for incompressible fluctuations and random interactions between the Alfvén wave packets, the velocity and magnetic turbulent spectra follow a ∼k ^−3/2 scaling.³

However, the assumption of isotropy in IK model for the magnetized plasma is quite strong. Goldreich and Sridhar (1995) proposed an MHD model for anisotropic Alfvénic fluctuations. In that theory, the cascade energy is carried by perpendicular fluctuations v _⊥ with wavelength ℓ _⊥=2π/k _⊥. The Alfvén time is the time scale along ${\bf B}$, τ _A =ℓ _∥/V _A , and the eddie turnover time τ _nl ≈ℓ _⊥/v _⊥ governs the energy exchange in the plane perpendicular to ${\bf B}$.⁴ Goldreich and Sridhar proposed that the turbulence is strong, so that these timescales are comparable, τ _nl ≈τ _A . This condition, called critical balance, implies that the nonlinear interaction occurs over a single Alfvén wave period. Using the argument of Kolmogorov, one can show that the perpendicular energy transfer rate is $\varepsilon(k_{\perp})\sim v_{\perp}^{3}/\ell_{\perp}$. Under the assumption of ε(k _⊥)=const, the power spectral density of k _⊥-fluctuations goes therefore like $\sim k_{\perp}^{-5/3}$. For the parallel energy transfer rate ε(k _∥) one gets $v^{2}_{\perp}V_{A}/\ell_{\|}$ and a spectrum $v_{\perp}^{2}/k_{\|}\sim k_{\parallel}^{-2}$. An interesting consequence of the Goldreich-Sridhar model is the following: since the cascade is carried by the perpendicular fluctuation spectrum (and indeed this property is reinforced as the energy arrives at larger wavenumbers, where the k-anisotropy becomes important k _⊥≫k _∥), the energy in the spectrum reaches dissipation scales (or characteristic plasma scales) in the perpendicular spectrum long before it does so in the parallel spectrum. This implies that relatively little energy of k _∥-fluctuations reaches the characteristic plasma scales due to the nonlinear cascade.

It should be pointed out that the model of Goldreich and Sridhar (1995) describes Alfvénic turbulence, i.e., the perpendicular magnetic δB _⊥ and velocity δv _⊥ fluctuations. This model has been extended to include the passive mixing of the compressive fluctuations by the Alfvénic turbulence (Goldreich and Sridhar 1995, 1997; Lithwick and Goldreich 2001; Schekochihin et al. 2009). However, the nature of compressible fluctuations observed in the solar wind, i.e. a passive scalar or an active turbulence ingredient, remains under debate.

Some theoretical results and solar wind observations suggest that ion cyclotron wave-particle interactions are an important source of heating for solar wind ions (Marsch and Tu 2001; Isenberg et al. 2001; Kasper et al. 2008, 2013; Bourouaine et al. 2010, 2011; Marsch and Bourouaine 2011; He et al. 2011b). However, this interpretation requires substantial turbulent energy at k _∥ ρ _i ≈1, that is in apparent contradiction to the Goldreich-Sridhar model and to the solar wind measurements described in the following section (Horbury et al. 2008; Podesta 2009; Luo and Wu 2010; Wicks et al. 2010; 2011; Chen et al. 2011a). This is another puzzle that has important ramifications for the coronal heating problem.

2.1 Scaling and Anisotropy as Observed in the Solar Wind

2.1.1 Magnetic Fluctuations

It has long been known that in the inertial range the power spectrum of magnetic field fluctuations in the solar wind is P(f)∝f ^−5/3, i.e. the same spectrum as for the velocity fluctuations in hydrodynamics turbulence (Kolmogorov 1941b; Frisch 1995). One might conclude that the turbulence in the solar wind is similar to that in a neutral fluid, like air. However, turbulence in a magnetofluid is radically different to that in a neutral fluid, due to the presence of a magnetic field which breaks the isotropy of the turbulence (Shebalin et al. 1983), leading to a correlation length parallel to the field longer than that across it, ℓ _∥>ℓ _⊥ (Matthaeus et al. 1990)—crudely, we can think of the turbulent eddies as being shorter perpendicular to the magnetic field than parallel to it, and more formally as having a dominance of turbulent power at wavevectors at large angles to the field, k _⊥>k _∥.

Measurements of the wave-vector anisotropy and of the corresponding spectra in the solar wind with one satellite are not trivial. A satellite provides time series measurements along its orbit; therefore, applying the Fourier (or wavelet) transform we obtain directly frequency spectra and not k-spectra. As we have discussed in the introduction, the Taylor hypothesis can be used, i.e. we can easily estimate k along the bulk flow through $k=\frac{2 \pi f}{V_{sw}}$. Thus, if ${\bf V_{sw}}$ is parallel to the mean field, the fluctuations with parallel wave vectors k _∥ will be measured, and if ${\bf V_{sw}}$ is perpendicular to ${\bf B}$, the satellite resolves well fluctuations with k _⊥. We denote the local flow-to-field angle as θ _BV . Figure 1 shows magnetic spectra in the fast high latitude solar wind measured by the Ulysses spacecraft (at distance of 1.38 to 1.93 AU from the Sun). As the spacecraft only measures wave vectors ${\bf k}$ parallel to ${\bf V_{sw}}$, for small flow-to-field angles θ _BV ∈[0,10]^∘, P _∥ (nT²/Hz) represents an E(k _∥) spectrum, and for quasi-perpendicular angles θ _BV ∈[80,90]^∘, P _⊥ (nT²/Hz), is the proxy of E(k _⊥). The total Fourier power, without separation into different angles is also shown. Within the energy injection range, the fluctuations are found to be isotropic, P _∥≃P _⊥, and both spectra follow an ∼f ⁻¹ power-law in agreement with previous observations (Bruno and Carbone 2005). In the inertial range one observes a bifurcation of the two spectra: the perpendicular spectrum follows the Kolmogorov’s slope, $E(k_{\perp })\sim k_{\perp}^{-5/3}$, while the parallel spectrum is steeper, $E(k_{\|})\sim k_{\|}^{-2}$. This result, initially seen in fast wind measured by Ulysses (Horbury et al. 2008) has been confirmed by several other studies (Podesta 2009; Luo and Wu 2010; Wicks et al. 2010, 2011; Chen et al. 2011a). These magnetic field spectral scaling observations provide an intriguing, if not unequivocal, connection to the Goldreich-Sridhar theory (Higdon 1984; Goldreich and Sridhar 1995). It is important to notice that the spectral anisotropy, shown in Fig. 1, is only observed while the local anisotropy analyses is used (Horbury et al. 2008). Such analysis consists in following the magnetic field direction as it varies in space and scale, which may cause the measured spectra to contain higher order correlations (Matthaeus et al. 2012).

Fig. 1

Trace of the spectral matrix of magnetic field corresponding to the field being parallel (θ _BV ∈[0,10]^∘) and perpendicular (θ _BV ∈[80,90]^∘) to the plasma flow are shown by blue lines, the total Fourier spectrum is shown in gray. The field-perpendicular spectrum P _⊥ dominates turbulence within the inertial range, it follows a power-law with the spectral index −5/3. The field-parallel spectrum P _∥ has lower power, is steeper and has the spectral slope −2. At the energy injection scales f<5⋅10⁻⁴ Hz (kρ _i <2⋅10⁻³) the fluctuations are isotropic and their spectrum follows ∼f ⁻¹. Courtesy of R. Wicks. The same figure as a function of kρ _i can be found in Wicks et al. (2010)

The importance of the local field for the turbulence anisotropy analysis has been pointed out already in Cho and Vishniac (2000), Maron and Goldreich (2001), Milano et al. (2001). The method proposed by Horbury et al. (2008), and used by Wicks et al. (2010) in Fig. 1, is equivalent in some sense to the one used in Milano et al. (2001) for numerical simulations, but can appear contradictory with the requirement of the ergodic theorem (equivalence between space and time averaging).⁵ However, there are practical implications that have to be considered: an individual packet of plasma passes a spacecraft once and never returns, meaning that the average magnetic field direction over many correlation lengths measured from a time series is not necessarily representative of the actual magnetic field direction at any point. Rather than taking simple time averages, here the local magnetic field direction (and local θ _BV ) to each fluctuation is measured, and then fluctuations that have similar directions are averaged. Precisely, in Fig. 1, Wicks et al. (2010) used many hundreds of observations in each direction, so the ergodicity is met, but in a non-conventional way.

Beyond the anisotropy of the fluctuations with respect to the magnetic field direction, (Boldyrev 2006) also suggested that the turbulence can be anisotropic with respect to the local fluctuation direction – and that this anisotropy will be scale dependent. Remarkably, in the solar wind observations there is some recent evidence for the scale-dependent alignment predicted by this theory at large scales (Podesta et al. 2009b) and for the local 3D anisotropy small scales (Chen et al. 2012b).

The nature of imbalanced turbulence is also a topic of current interest. Alfvén waves can propagate parallel or anti-parallel to the magnetic field. Without the presence of both senses, the fluctuations are stable and will not decay. However, the level of imbalance is highly variable in the solar wind (fast wind is typically dominated by Alfvénic fluctuations propagating anti-sunward).

2.1.2 Velocity Fluctuations

Velocity fluctuations in the solar wind appear to have a spectrum significantly shallower than the magnetic field, with a spectral index near −3/2 (Grappin et al. 1991; Salem 2000; Mangeney et al. 2001; Podesta et al. 2007; Salem et al. 2009; Chen et al. 2011b, 2013b; Boldyrev et al. 2011; Borovsky 2012b). Figure 2 shows (a) a velocity spectrum and (b) a compensated spectrum with the f ^3/2 function obtained from Wind measurements using the Haar wavelet technique (Salem et al. 2009). Such a spectrum was predicted by the IK phenomenology for Alfvénic fluctuations propagating in opposite directions along ${\bf B}$. However, in this model, both magnetic field and velocity spectra are expected to follow the ∼k ^−3/2 power-law. The difference of the solar wind inertial range with a pure Alfvénic turbulence described in the IK model (and with the anisotropic Goldreich-Sridhar model) is also an excess of magnetic energy with respect to the kinetic energy, see Fig. 8 in Salem et al. (2009). How can the difference between the velocity and the magnetic spectra, and the excess of magnetic energy in the solar wind, be explained? Direct simulations of incompressible MHD usually show an excess of magnetic energy as well. It has been attributed to a local dynamo effect which balances the linear Alfvén effect (Grappin et al. 1983). The difference between magnetic and kinetic energies is usually called in the literature “residual energy”. The residual energy has been shown to follow a definite scaling which is related to the scaling of the total energy spectrum (Grappin et al. 1983; Müller and Grappin 2005), see also (Boldyrev and Perez 2009; Boldyrev et al. 2012; Chen et al. 2013b).

Fig. 2

(a) Spectrum of velocity fluctuations of V _y (GSE) component, measured by Wind as a function of the frequency in the spacecraft frame, the data have been published in Salem et al. (2009). (b) Compensated spectrum by an f ^3/2 law: the resulting function is flat for f>10⁻⁴ Hz. Courtesy of C. Salem

Another possible explanation of the difference between the observed magnetic and velocity spectra can be related to the presence of compressible fluctuations, not negligible for the energy exchange between scales.

2.1.3 Density fluctuations

Turbulent fluctuations within the inertial range are not only anisotropic in space (or in ${\bf k}$), but as well in their amplitudes with respect to ${\bf B}$. As we have discussed in the introduction, the non-compressive, Alfvénic turbulence dominates the solar wind at MHD scales, δB _⊥≫δB _∥. Nevertheless, there is a sub-dominant population of δB _∥ and density δρ fluctuations always present, with scaling properties suggestive of a turbulent cascade (Celnikier et al. 1983; Marsch and Tu 1990; Manoharan et al. 1994; Kellogg and Horbury 2005; Hnat et al. 2005; Issautier et al. 2010; Chen et al. 2011b). Figure 3 shows an example of an electron density spectrum measured by the ISEE 1-2 satellites in the [6⋅10⁻⁴,5] Hz frequency range (Celnikier et al. 1983). At MHD scales, f<10⁻¹ Hz, the K41 scaling is observed. At higher frequencies, i.e. around ion scales, one observes a spectrum flattening and then another steep spectrum. These high-frequency features will be discussed in more details in Sect. 3.

Fig. 3

Spectrum of electron density fluctuations n _e measured by the ISEE 1–2 spacecraft: two distinct power-laws are observed, the spectrum follows ∼f ^{−1.67±0.05} within the frequency range [10⁻³,6⋅10⁻²] Hz, the spectrum is about f ^−0.9±0.2 at f>6⋅10⁻² Hz. Around 1–2 Hz the spectrum seems to change again, however, this high frequency range is too narrow to make any firm conclusion (the maximal measured frequency is 5 Hz). Figure from Celnikier et al. (1983)

The origin of the compressible fluctuations in the solar wind is not clear, as far as fast and slow mode waves are strongly damped at most propagation angles. Howes et al. (2012a) have recently argued, based on the dependence of the δB _∥-δρ correlation on the plasma beta β (ratio of thermal to magnetic pressure), that these fluctuations are slow mode and they appear to be anisotropic in wave-vectors (He et al. 2011a). Chen et al. (2012b) measured the δB _∥ fluctuations to be more anisotropic than the Alfvénic component in the fast solar wind, suggesting this as a possible reason why they are not heavily damped (Schekochihin et al. 2009). Yao et al. (2011) observe a clear anti-correlation between electron density and the magnetic field strength at different time scales (from 20 s to 1 h): the authors interpret their observations as multi-scale pressure-balanced structures which may be stable in the solar wind. This interpretation is consistent with the observation of intermittency in electron density fluctuations by the Ulysses spacecraft (Issautier et al. 2010).

2.2 Intermittency

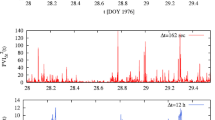
In hydrodynamics, the amplitude of the fluctuations at a given scale—and hence the local energy transfer rate—is variable, a property known as intermittency, i.e. turbulence and its dissipation are non-uniform in space (Frisch 1995). This results in the turbulence being bursty, which can be easily seen from the test of regularity of turbulent fluctuations (Mangeney 2012). Usually, turbulent fluctuations at different time scales τ are approximated by increments calculated at these scales, δy _τ =y(t+τ)−y(t). The time averages of these increments are called “structure functions” (for more details see the paper by Dudok de Wit et al. 2013 in this book). In the presence of intermittency, the scaling of higher order moments of the structure functions diverges from the simple linear behavior expected for non-intermittent, Gaussian fluctuations: in essence, at smaller scales, there are progressively more large jumps, as the turbulence generates small scale structures. This behavior is also observed in the solar wind on MHD scales (Burlaga 1991; Tu and Marsch 1995; Carbone et al. 1995; Sorriso-Valvo et al. 1999; Veltri and Mangeney 1999; Veltri 1999; Salem 2000; Mangeney et al. 2001; Bruno et al. 2001; Sorriso-Valvo et al. 2001; Hnat et al. 2003; Veltri et al. 2005; Bruno and Carbone 2005; Leubner and Voros 2005; Jankovicova et al. 2008; Greco et al. 2009, 2010; Sorriso-Valvo et al. 2010). Figure 4 shows probability distribution functions (PDF) of the tangential component of the standardized magnetic field fluctuations ΔB _y =δB _y /σ(δB _y ), σ being the standard deviation of δB _y (in RTN coordinates⁶) computed for three different time scales τ. Intermittency results in the change of shape, from the large scale Gaussian to the small scale Kappa functions.

Fig. 4

Probability distribution functions (PDFs) of the tangential component of the standardized magnetic field fluctuations ΔB _y (in RTN coordinates) computed for three different time lags, as indicated in the legend. PDFs were estimated using 6 second Helios 2 data recorded in a stationary slow wind stream near 0.3 AU on days 100 to 102 of 1976. The data used here were published previously in Bruno et al. (2004)

Intermittency is a crucial ingredient of turbulence. Being related to the full statistical properties of the fields, its characterization can give an important insight on the nature of turbulence and on possible dissipation mechanisms of turbulent energy.

Note, as well, that as far as the third-order moment of fluctuations is related to the energy dissipation rate and is different from zero (see the K4/5 law, Eq. (1)), turbulence must shows some non-Gaussian features.

Solar wind observations have shown that the intermittency of different fields can be remarkably different. In particular, it has been observed in several instances that the magnetic field is generally more intermittent than the velocity (Sorriso-Valvo et al. 1999, 2001). The possibility that this implies that magnetic structures are passively convected by the velocity field has been discussed, but no clear evidence was established, so that this is still an open question (Bershadskii and Sreenivasan 2004; Bruno et al. 2007).

The use of data from Helios 2 spacecraft, which explored the inner heliosphere reaching about 0.3 AU, has allowed to study the radial evolution of intermittency, and its dependency on the wind type (fast or slow) (Bruno et al. 2003). The fast wind has revealed an important increase of intermittency as the wind blows away from the Sun, while the slow wind is less affected by the radial distance R. This suggests that some evolution mechanism must be active in the fast solar wind. This could be either due to the slower development of turbulence in the fast wind, with respect to the slow wind, or to the presence of superposed uncorrelated Alfvénic fluctuations, which could hide the structures responsible for intermittency in the fast wind closer to the Sun. These uncorrelated Alfvénic fluctuations, ubiquitous in the fast wind, are indeed observed to decay with R, as suggested for example by a parametric instability model (Malara et al. 2000, 2001; Bruno et al. 2003, 2004).

The ultimate responsible for emergence of intermittency are strong fluctuations of the fields with coupled phases over a finite range of scales. These are often referred to as coherent structures. Figure 5 shows an example of a coherent structure responsible for the non-Gaussian PDF tails in Fig. 4 at small scales: a shock wave with its normal quasi-perpendicular to the local mean field (Veltri and Mangeney 1999; Salem 2000; Veltri et al. 2005). This kind of structures may be responsible for the dissipation of turbulent energy in the collisionless solar wind.

Fig. 5

Example of a coherent structure responsible for the non-Gaussian PDF tails in Fig. 4 at small scales: a quasi-perpendicular shock wave at a time scale of the order of τ=30 sec. Measurements of $\delta{\bf B}$ in the local minimum variance frame (solid lines) and velocity fluctuations $\delta{\bf v}$ in the same frame (dashed lines) as measured by Wind satellite in the fast solar wind (courtesy of C. Salem)

A complication in the solar wind is that sharp structures, discontinuities, are ubiquitous. Discontinuities typically involve a rotation in the magnetic field direction, and sometimes variations in velocity, field magnitude and other plasma properties such as density and even temperature and composition (Owens et al. 2011). Parameters such as composition do not change much after the wind leaves the solar corona, so these might have been generated at its source. However, the vast majority of structures have no such signature: are these also part of the structure of the solar wind (Borovsky 2008), or are they generated dynamically by the turbulence (Greco et al. 2009, 2012)? These structures seem to be associated with enhanced temperature of the solar wind (Osman et al. 2011; Wu et al. 2013), so they might represent a source of energy dissipation via reconnection or enhanced damping. Discontinuities, as sharp jumps, also contribute to the intermittency of the solar wind turbulence. To what extent is the observed intermittency inherent to the plasma turbulence, therefore, as opposed to being an artifact of its generation in the corona? This is a currently unresolved issue and the topic of many recent works (Servidio et al. 2011, 2012; Zhdankin et al. 2012; Borovsky 2012a; Osman et al. 2012; Wu et al. 2013; Karimabadi et al. 2013).

2.3 Energy Transfer Rate

As we have mentioned in the introduction, any turbulent flow is characterized by power-law energy spectra, presence of intermittency and linear dependence between the third order structure function and scale. This last property is the only exact result for hydrodynamic turbulence, known as the K4/5 law, see Eq. (1). In plasmas, the incompressible MHD version of the K4/5 law has been obtained by Politano and Pouquet (1998) by using the Elsasser fields ${\bf Z^{\pm}}(t)={\bf v}(t)\pm{\bf b}(t)/\sqrt{4\pi\rho}$ in place of velocity δv in Eq. (1) (${\bf v}(t)$ and ${\bf b}(t)$ being the time dependent solar wind velocity and magnetic field).

The MHD equations can be conveniently written in terms of Elsasser variables ${\bf Z^{\pm}}$ as

$$ \frac{\partial{\bf Z^{\pm}}}{\partial t} + \bigl({\bf Z^\mp} \cdot \nabla \bigr) {\bf Z^\pm} = -\nabla P + \eta^\prime\nabla^2 {\bf Z^{\pm }} \; , $$

(2)

where P is the total pressure (magnetic plus kinetic), and η′=η=ν is a dissipation coefficient⁷. Non-linear terms $({\bf Z^{\mp}} \cdot\nabla ) {\bf Z^{\pm}}$ in Eq. (2) are responsible for the transfer of energy between fluctuations at different scales, originating the turbulent cascade and the typical Kolmogorov spectrum. The MHD version of the K4/5 law for ΔZ ⁺ is obtained by subtracting Eq. (2) for Z ⁻ from the one for Z ⁺, evaluated at two generic points separated by the scale ℓ=V _sw τ along the flow direction, and then by multiplying the result by ΔZ ⁺.

This provides an evolution equation for the pseudo-energy flux,⁸ which includes terms accounting for anisotropy, inhomogeneity and dissipation. Under the hypotheses of isotropy, local homogeneity and vanishing dissipation (i.e. within the inertial range, far from the dissipation scale), the simple linear relation can be retrieved in the stationary state (Politano and Pouquet 1998):

$$ Y^\pm(\tau) = \bigl\langle\bigl|\Delta{\bf Z}^\pm( \tau,t)\bigr|^2\, \Delta Z^\mp _R(\tau,t) \bigr \rangle= {4 \over3} \,\varepsilon^\pm\, \ell, $$

(3)

where $Z^{\mp}_{R}$ is the radial component (i.e., along the mean solar wind flow ${\bf V}_{sw}$) of the Elsasser fields. For a detailed description of the derivation, see e.g. Danaila et al. (2001), Carbone et al. (2009a).

The turbulent cascade pseudo-energy fluxes ε ^± are defined as the trace of the dissipation rate tensors

$$\varepsilon_{ij}^{\pm} = \eta\bigl\langle\bigl( \partial_i Z_i^{\pm}\bigr) \bigl( \partial_i Z_j^{\pm}\bigr) \bigr\rangle. $$

ε ^± describe the energy transfer rate and dissipation rate between the Elsasser field structures on scales within the inertial range of MHD turbulence.

The relation (3) was first observed in numerical simulations of two dimensional MHD turbulence (Sorriso-Valvo et al. 2002; Pietarila Graham et al. 2006), and later in solar wind samples (MacBride et al. 2005; Sorriso-Valvo et al. 2007; MacBride et al. 2008), despite the observational difficulties (Podesta et al. 2009a) and the fact that solar wind turbulence is not isotropic (Sect. 2.1). An example of linear dependence between Y ⁻ and the time scale τ from Ulysses high latitude data is shown in Fig. 6.

Fig. 6

The third order moment linear scaling law as evaluated in the 11 day time interval starting on day 218 of 1996, during the high latitude scan of Ulysses spacecraft. The heliocentric distance was 4.2 AU, the heliolatitude was 30^∘, and the mean wind speed of the sample was 735 km/s. The linear fit predicted by the law (3), is indicated. For this sample, the pseudo-energy transfer rate is estimated to be ε ⁻=212 J kg⁻¹ s⁻¹

The observation of the third order moment scaling is particularly important, since it suggests the presence of a (direct or inverse) turbulent cascade⁹ as the result of nonlinear interactions among fluctuations. It also suggests that solar wind turbulence is fully developed, as the dissipative effects have to be neglected in order to observe the linear scaling. It defines rigorously the extension of the inertial range, where a Kolmogorov like spectrum can be expected. In solar wind, the inertial range, as defined by the law of Politano and Pouquet (1998), Eq. (3), is found to be extremely variable, and can reach scales up to one day or even more (Sorriso-Valvo et al. 2007; Marino et al. 2012), much larger than usually assumed following typical estimates from the analysis of turbulent spectra. The variability of the inertial range extension, i.e. the range of scales where the linear relation (3) is observed, is in agreement with earlier multifractal analysis of solar wind fluctuations (Burlaga 1993). Moreover, recent results, obtained through conditioned analysis of solar wind fluctuations, have confirmed that, for high cross-helicity states, i.e. when $\langle{\bf v\cdot b}\rangle/(\langle v^{2}\rangle+\langle b^{2}\rangle)$ is high, the inertial range observed in the spectrum extends to such larger scales (Wicks et al. 2013). It will be interesting as well to verify the influence of the solar wind expansion time τ _exp (in comparison with the non-linear time) on the extension of the inertial range (see our discussion in the introduction).

The third order moment law provides an experimental estimate of the mean energy transfer rates ε ^±, a measurement which is not possible otherwise, as the solar wind dissipation mechanisms (and so the viscosity η) are unknown. Solar wind energy transfer rates have been shown to lie between ∼0.1 kJ kg⁻¹ s⁻¹ (in Ulysses high latitude fast wind data, far from the Earth) and up to ∼10 kJ kg⁻¹ s⁻¹ in slow ecliptic wind at 1 AU (Sorriso-Valvo et al. 2007; Marino et al. 2008, 2012; MacBride et al. 2008; Smith et al. 2009). The rate of occurrence of the linear scaling in the solar wind time series, and the corresponding energy transfer rate, have been related to several solar wind parameters. For example, the energy transfer rate has been shown to anti-correlate with the cross-helicity level (Smith et al. 2009; Stawarz et al. 2010; Marino et al. 2011, 2012; Podesta 2011), confirming that alignment between velocity and magnetic field reduces the turbulent cascade, as expected for Alfvénic turbulence (Dobrowolny et al. 1980; Boldyrev 2006). Relationships with heliocentric distance and solar activity have also been pointed out, with controversial results (Marino et al. 2011, 2012; Coburn et al. 2012).

The estimation of the turbulent energy transfer rate has also shown that the electromagnetic turbulence may explain the observed solar wind non-adiabatic profile of the total proton temperature (Vasquez et al. 2007; Marino et al. 2008; MacBride et al. 2008; Stawarz et al. 2009). However, this explanation does not take into account a possible ion temperature anisotropy, known to be important in the solar wind (see Sect. 3.2). Indeed, the weakly collisional protons exhibit important temperature anisotropies (and complicated departures from a Maxwellian shape, Marsch et al. 1982) and they have non double-adiabatic temperatures profiles. Helios observations indicate that protons need to be heated in the perpendicular direction from 0.3 to 1 AU, but in the parallel direction they need to be cooled at 0.3 AU. This cooling rate gradually transforms to a heating rate at 1 AU (Hellinger et al. 2011, 2013). It is not clear if the turbulent cascade may cool the protons in the parallel direction (and transform this cooling to heating by 1 AU).

The phenomenological inclusion of possible contributions of density fluctuations to the turbulent energy transfer rate resulted in enhanced energy flux, providing a more efficient mechanism for the transport of energy to small scales (Carbone et al. 2009b).

Anisotropic corrections to the third order law have also been explored using anisotropic models of solar wind turbulence (MacBride et al. 2008; Carbone et al. 2009a; Stawarz et al. 2009, 2010; MacBride et al. 2010; Osman et al. 2011).

It is important to keep in mind that the solar wind expansion, the large scale velocity shears and the stream-stream interactions importantly affect the local turbulent cascade (Stawarz et al. 2011; Marino et al. 2012). Their effect on the turbulent energy transfer rate needs to be further investigated (Wan et al. 2009; Hellinger et al. 2013).

3 Turbulence at Kinetic Scales

At 1 AU, the MHD scale cascade finishes in the vicinity of ion characteristic scales ∼0.1–0.3 Hz in the spacecraft frame. Here the turbulent spectra of plasma parameters (magnetic and electric fields, density, velocity and temperature) change their shape, and steeper spectra are observed at larger wave-numbers or higher frequencies, e.g. (Leamon et al. 1998; Bale et al. 2005; Alexandrova et al. 2007; Chen et al. 2012a; Šafránková et al. 2013). There is a range of terminology used to describe this range, including “dissipation range”, “dispersion range” and “scattering range”. The possible physics taking place here includes dissipation of turbulent energy (Leamon et al. 1998, 1999, 2000; Smith et al. 2006; Schekochihin et al. 2009; Howes et al. 2011b), a further small scale turbulent cascade (Biskamp et al. 1996; Ghosh et al. 1996; Stawicki et al. 2001; Li et al. 2001; Galtier 2006; Alexandrova et al. 2007, 2008; Schekochihin et al. 2009; Howes et al. 2011b; Rudakov et al. 2011; Boldyrev and Perez 2012) or a combination of both.

The transition from the MHD scale cascade to the small scale range is sometimes called the ion spectral break due to the shape of the magnetic field spectrum and to the scales at which it occurs. The physical processes responsible for the break and the corresponding characteristic scale are under debate. If the MHD scale cascade was filled with parallel propagating Alfvén waves, the break point would be at the ion cyclotron frequency f _ci , where the parallel Alfvén waves undergo the cyclotron damping. The oblique kinetic Alfvén wave (KAW) turbulence is sensitive to the ion gyroradius ρ _i (Schekochihin et al. 2009; Boldyrev and Perez 2012) and the transition from MHD to Hall MHD occurs at the ion inertial length λ _i (Galtier 2006; Servidio et al. 2007; Matthaeus et al. 2008, 2010).

Recent Cluster measurements of magnetic fluctuations up to several hundred Hz in the solar wind (Alexandrova et al. 2009, 2012; Sahraoui et al. 2010) show the presence of another spectral change at electron scales. At scales smaller than electron scales, the plasma turbulence is expected to convert from electromagnetic to electrostatic (with the important scale being the Debye length, see, e.g., Henri et al. 2011), but this is beyond the scope of the present paper.

The energy partitioning at kinetic scales, the spectral shape and the properties of the small scale cascade are important for understanding the dissipation of electromagnetic turbulence in collisionless plasmas.

3.1 Turbulence Around Ion Scales

Figure 7 shows an example of the solar wind magnetic field spectrum covering the end of the MHD inertial range and ion scales. The data are measured at 1 AU by Cluster/FGM (open circles) and Cluster/STAFF-SC (filled circles), which is more sensitive than FGM at high frequencies. One may conclude that the transition from the inertial range to another power-law spectrum is around ion scales, such as the ion cyclotron frequency f _ci =0.1 Hz, the ion inertial scale λ _i corresponding to $f_{\lambda _{i}}=V_{sw}/(2\pi\lambda_{i})\simeq0.7$ Hz and the ion Larmor radius ρ _i appearing at $f_{\rho_{i}}=V_{sw}/(2\pi\rho_{i})\simeq1$ Hz. However, which of these ion scales is responsible for the spectral break is not evident from Fig. 7.

Fig. 7

Wavelet spectrum of magnetic fluctuations measured by Cluster in the solar wind up to 12.5 Hz for the time interval analyzed in Alexandrova et al. (2008). The Cluster/FGM spectrum is represented by open circles, Cluster/Search Coil (STAFF-SC) spectrum, by filled circles. The characteristic ion scales are marked by vertical bars

Leamon et al. (2000) performed a statistical study of the spectral break values f _b at 1 AU for different ion beta conditions, β _i =nk _B T _i /(B ²/2μ ₀)∈[0.03,3]¹⁰, with μ ₀ being the vacuum magnetic permeability. The best correlation is found with the ion inertial length while taking into account the 2D nature of the turbulent fluctuations, i.e. k _⊥≫k _∥, see Fig. 8(a). A larger statistical sample of 960 spectra shows the dependence between f _b , and $f_{\lambda_{i}}\frac{B}{\delta B_{b}}$, where δB _b /B is the relative amplitude of the fluctuations at the break scale (Markovskii et al. 2008). This result is still not explained. But, it is important to keep in mind that δB _b /B is controlled by the ion instabilities in the solar wind when the ion pressure is sufficiently anisotropic (Bale et al. 2009), see Sect. 3.2 for more details.

Fig. 8

(a) Observed ion break frequency f _b as a function of $f_{\lambda_{i}}=V_{sw}\sin\theta_{BV}/2\pi\lambda_{i}$, a correlation of 0.6 is observed (Leamon et al. 2000). (b) Radial evolution of f _b compared with the radial evolution of f _ci , f _ρ =V _sw /2πρ _i and f _λ =V _sw /2πλ _i : none of the ion scales follow the break (Perri et al. 2010). (c) Radial evolution of f _b (black dots) compared with f _ci (black triangles), $f_{\rho_{p}}=\sin\theta _{BV}V_{sw}/2\pi\rho_{p}$ (red diamonds) and $f_{\lambda_{p}}=\sin\theta _{BV}V_{sw}/2\pi\lambda_{p}$ (blue diamonds) (Bourouaine et al. 2012)

A different approach has been used by Perri et al. (2010): the authors studied the radial evolution of the spectral break for distances R∈[0.3,5] AU. They showed that the ion break frequency is independent of the radial distance (see Fig. 8(b)). Bourouaine et al. (2012) explained this result by the quasi-bidimensional topology of the turbulent fluctuations, i.e. k _⊥≫k _∥. When this wave vector anisotropy is taken into account, the Doppler shifted frequency $2\pi f={\bf k\cdot V_{sw}}$ can be approximated by kV _sw sinθ _BV . It appears that the ion inertial scale stays in the same range of frequencies as f _b , and a correlation of 0.7 is observed between f _b and $f_{\lambda_{i}}=V\sin \theta_{BV}/2\pi\lambda_{i}$, see Fig. 8(c).

As we have discussed above, the transition to kinetic Alfvén turbulence happens at the ion gyroradius ρ _i scale (Schekochihin et al. 2009; Boldyrev et al. 2012), while the dispersive Hall effect becomes important at the ion inertial length λ _i . Results of Leamon et al. (2000) and Bourouaine et al. (2012) indicate, therefore, that the Hall effect may be responsible for the ion spectral break. Note that Bourouaine et al. (2012) analyzed Helios data only within fast solar wind streams with β _i <1, i.e. when λ _i >ρ _i .¹¹ It is quite natural that the largest characteristic scale (or the smallest characteristic wave number) affects the spectrum first (Spangler and Gwinn 1990). It will be interesting to verify these results for slow solar wind streams and high β _i regimes.

Just above the break frequency, f>f _b , the spectra are quite variable. Smith et al. (2006) show that within a narrow frequency range [0.4–0.8] Hz, the spectral index α varies between −4 and −2. This result was obtained using ACE/FGM measurements. However, one should be very careful while analyzing FGM data at frequencies higher than the ion break (i.e. at f>0.3 Hz), where the digitalization noise becomes important (Lepping et al. 1995; Smith et al. 1998; Balogh et al. 2001). For example, in Fig. 7 the Cluster/FGM spectrum deviates from the STAFF spectrum at f≥0.7 Hz.¹²

Figure 9 shows several combined spectra, with Cluster/FGM data at low frequencies and Cluster/STAFF data at f>f _b . The spectra are shown as a function of the wave-vector k _⊥ ¹³. The spectra are superposed at $k_{\perp} > k_{\rho_{i}}, \; k_{\lambda_{i}}$, i.e. at scales smaller than all ion scales: while at these small scales all spectra follow the same law, around ion scales $k_{\rho_{i}}$ and $k_{\lambda_{i}}$ (named here a transition range) one observes a divergence of the spectra. The origin of this divergence is not completely clear. It is possible that ion damping (e.g. Denskat et al. 1983; Sahraoui et al. 2010), a competition between the convective and Hall terms (Kiyani et al. 2013) or ion anisotropy instabilities (Gary et al. 2001; Matteini et al. 2007, 2011; Bale et al. 2009) may be responsible for the spectral variability within the transition range.

Fig. 9

7 solar wind spectra, analyzed in Alexandrova et al. (2009, 2010) under different plasma conditions as a function of the wave-vector k _⊥ perpendicular to the magnetic field. The spectra are superposed with a normalization factor E ₀ at scales smaller than all ion scales: one observes divergence of the spectra in the transition range around the ion scales $k_{\rho_{i}}$ and $k_{\lambda_{i}}$

One of the important properties of the transition range is that the turbulent fluctuations become more compressible here (Leamon et al. 1998; Alexandrova et al. 2008; Hamilton et al. 2008; Turner et al. 2011; Salem et al. 2012; Kiyani et al. 2013). Let us define the level of compressibility of magnetic fluctuations as $\delta B_{\|}^{2}/\delta B_{tot}^{2}$, with $\delta B_{tot}^{2}$ being the total energy of the turbulent magnetic field fluctuations at the same scale as δB _∥ is estimated. If in the inertial range the level of compressibility is about 5 %, for f>f _b it can reach 30 % and it depends on the plasma beta β _i (Alexandrova et al. 2008; Hamilton et al. 2008). The increase of the compressibility at kinetic scales has been attributed to the compressive nature of kinetic Alfvén or whistler turbulence (Gary and Smith 2009; Salem et al. 2012; TenBarge et al. 2012). On the other hand, it can be described by the compressible Hall MHD (Servidio et al. 2007). In particular, in the this framework, different levels of compressibility can also explain the spectral index variations in the transition range (Alexandrova et al. 2007, 2008).

The flattening of the electron density spectrum from ∼f ^−5/3 to ∼f ⁻¹, seen in Fig. 3, is observed within the same range of scales as the increase of the magnetic compressibility. The shape of this flattening is consistent with the transition between MHD scale Alfvénic turbulence and small scale KAW turbulence (Chandran et al. 2009; Chen et al. 2013a). More recently, Šafránková et al. (2013) measured the ion density spectrum within the transition range, finding similar results, as expected from the quasi-neutrality condition. In addition, they showed the ion velocity and temperature spectra in this range to be steeper with slopes around −3.4. An example of such spectra is shown in Fig. 10.

Fig. 10

Spectra of ion moments, (a) density, (b) velocity, (c) ion thermal speed, up to ∼3 Hz as measured by Spektr-R/BMSW (Bright Monitor of Solar Wind) in the slow solar wind with V _sw =365 km/s and β _p ≃0.2. Figure from Šafránková et al. (2013)

The transition range around ion scales is also characterized by magnetic fluctuations with quasi-perpendicular wave-vectors k _⊥>k _∥ and a plasma frame frequency close to zero (Sahraoui et al. 2010; Narita et al. 2011; Roberts et al. 2013). Sahraoui et al. (2010) interpret these observations as KAW turbulence, although Narita et al. (2011) found no clear dispersion relation. Magnetic fluctuations with nearly zero frequency and k _⊥≫k _∥ can also be due to non-propagative coherent structures like current sheets (Veltri et al. 2005; Greco et al. 2010; Perri et al. 2012), shocks (Salem 2000; Veltri et al. 2005; Mangeney et al. 2001), current filaments (Rezeau et al. 1993), or Alfvén vortices propagating with a very slow phase speed ∼0.1V _A in the plasma frame (Petviashvili and Pokhotelov 1992; Alexandrova 2008). Such vortices are known to be present within the ion transition range of the planetary magnetosheath turbulence, when ion beta is relatively low β _i ≤1 (Alexandrova et al. 2006; Alexandrova and Saur 2008). Recent Cluster observations in the fast solar wind suggest that the ion transition range can be populated with KAWs and Alfvén vortices (Roberts et al. 2013).

As well as the spectrum of energy, the spectrum of magnetic helicity is also used to diagnose solar wind turbulence, and can tell us more details about the nature of the fluctuations (Matthaeus et al. 1982; Howes and Quataert 2010). Magnetic helicity is defined as 〈A⋅B〉, where B=∇×A, with A being the vector potential. It has been measured that at ion scales the magnetic helicity is anisotropic (He et al. 2011b). Figure 11 shows the reduced magnetic helicity¹⁴ σ _m as a function of the time scale and of the local flow-to-field angle θ _BV . The authors found that, at time scales corresponding to the ion scales (1 to 10 s), there was a significant positive (negative) magnetic helicity signature for inward (outward) directed magnetic field in the parallel direction (i.e. for θ _BV close to 0 or to 180). This is consistent with left-hand parallel propagating Alfvén-ion-cyclotron waves. In the perpendicular direction, θ _BV ≃90^∘, they found a magnetic helicity signature of the opposite sense: positive (negative) for outward (inward) field, consistent with the right-hand polarization, inherent to both whistler and kinetic Alfvén waves. Outside the range of frequencies (0.1–1) Hz, the magnetic helicity was generally zero. Podesta and Gary (2011) found the same result using Ulysses data and suggested the source of the parallel waves to be pressure anisotropy instabilities, which we will now discuss in more details.

Fig. 11

Magnetic helicity σ _m for an outward magnetic sector as measured by STEREO spacecraft as a function of time scale τ (s) and angle to the magnetic field θ _VB (He et al. 2011b)

3.2 Ion Scale Instabilities Driven by Solar Wind Expansion and Compression

The turbulent fluctuations, while cascading from the inertial range to the kinetic scales, will undergo strong kinetic effects in the vicinity of such ion scales as the ion skin depth or inertial scale λ _i , and near the thermal gyroradius ρ _i . At these small scales ion temperature anisotropy instabilities can occur (Gary et al. 2001; Marsch 2006; Matteini et al. 2007, 2011; Bale et al. 2009), and may remove energy from, or also inject it into, the turbulence.

As the solar wind expands into space, mass flux conservation leads to a density profile that falls roughly as 1/R ² (beyond the solar wind acceleration region); the magnetic field decays similarly, although the solar rotation and frozen flux condition ensure an azimuthal component to the field. If the solar wind plasma remains (MHD) fluid-like, then the double-adiabatic conditions (also called the Chew-Goldberger-Low or ‘CGL’) will apply (Chew et al. 1956) and will serve to modify adiabatically the plasma pressure components such that:

$$\begin{aligned} & \frac{p_{||} B^2}{\rho^3} = \mathrm{const} \end{aligned}$$

(4)

$$\begin{aligned} & \frac{p_{\perp}}{\rho B} = \mathrm{const}, \end{aligned}$$

(5)

with p _∥,⊥ being the ion pressure along (∥) and perpendicular (⊥) to the mean field ${\bf B}$.

Taken together, the CGL conditions suggest that an adiabatically transported fluid element should see its temperature ratio T _⊥/T _|| fall as approximately 1/R ² between 10 and 100R _s , as the solar wind expands outward (R _s being the radius of the Sun). Therefore a parcel of plasma with an isotropic temperature (T _⊥/T _||∼1) at the edge of the solar wind acceleration region (∼10R _s ) will arrive at 1 AU in a highly anisotropic state T _||∼100T _⊥, if it remains adiabatic. Such a large temperature anisotropy has never been observed in the solar wind because the CGL conditions do not take into account wave-particle interactions or kinetic effects, which can control plasma via different types of instabilities.

Several early authors studied this possibility and looked for evidence of instability (Gary et al. 1976, 1996; Kasper 2002; Hellinger et al. 2006; Matteini et al. 2007; Bourouaine et al. 2010). Relatively recent results of Bale et al. (2009) using well-calibrated, statistical measurements from the Wind spacecraft have shown that the proton temperature anisotropy T _⊥/T _|| is constrained by the β _|| ¹⁵-dependent thresholds for the oblique firehose instability (for T _⊥/T _||<1) and the mirror-mode instability (for T _⊥/T _||>1) suggesting that the growth of ion-scale fluctuations acts to isotropize the plasma near the thresholds (Gary 1993). Indeed, a build-up of magnetic fluctuation power is observed near these thresholds (Bale et al. 2009) and the fluctuations seen near the mirror threshold and for β _||>1 are compressive, as would be expected from the growth of mirror waves (Hasegawa 1969). Figure 12 (left) shows time series data of magnetic and velocity fluctuations as the solar wind approaches the oblique firehose instability threshold: the top panel shows measurements of the ion temperature anisotropy (black dots) and the theoretical instability thresholds (Hellinger et al. 2006) as dotted lines. When the solar wind approaches the firehose threshold (black dotted line), enhanced fluctuation power is observed in the perpendicular components of the magnetic field and velocity, consistent with Alfvénic-like fluctuations excited by the firehose instability (Hellinger and Matsumoto 2000, 2001). Figure 12 (right) shows an example when the plasma conditions are close to both, mirror and firehose instability thresholds, and when both types of fluctuations, Alfvénic and compressive, are excited.

Fig. 12

(Left) time series data of measured proton temperature anisotropy (dots) and instability thresholds (top panel), of magnetic (2nd panel) and velocity (3rd panel) vector fluctuations in a field-aligned coordinate system (FAC), using 3 second measurements from the Wind/3DP instrument; red lines indicate fluctuations parallel to the mean field ${\bf B}$, p1 (violet) and p2 (green) represent the two perpendicular components. As the measured proton anisotropy approaches the oblique firehose instability threshold (black dotted line in the top panel), Alfvénic-like fluctuations are excited and visible as perpendicular magnetic and velocity perturbations. (Right) the same format as left figure, but for the high ion beta regime, when the plasma conditions were close to both, mirror and firehose instability thresholds: both types of fluctuations, Alfvénic-like and compressive, are excited

Figure 13 is reproduced from Bale et al. (2009) and shows statistically the effect seen in Fig. 12. One continuing puzzle here is the following: the instability thresholds, with the rate γ≃10⁻³2πf _ci , calculated by Hellinger et al. (2006) suggest that the ion cyclotron instability should be unstable at values of T _⊥/T _|| lower than the mirror instability (at low β _∥), however there is no clear evidence in the data of an ion cyclotron limit. One reason for this may be that the mirror mode is non-propagating, and therefore more effective in pitch angle scattering. In any case, this is unresolved.

Fig. 13

Temperature anisotropy T _⊥/T _|| vs plasma parallel beta β _|| from Bale et al. (2009). The upper panel shows the constraint of plasma by the mirror (upper dashed line) and oblique firehose (lower dashed line) instabilities, as shown by Hellinger et al. (2006). The second panel shows a statistical enhancement of magnetic fluctuations δB/B (calculated at f=0.3 Hz, i.e. close to the ion spectral break) near the thresholds and at higher β _||. The third panel shows the distribution of the magnetic compressibility δB _||/δB (at ion scales as well) and is consistent with mirror instability near that threshold. The fourth panel shows the collisional age of the ions (i.e. the number of collisions suffered by a thermal ion between the Sun and the spacecraft at 1 AU) in the same parameter plane

The clear existence of instability-limited anisotropies, and the measurement of the associated ion-scale fluctuations, bring to light a very important question: how much of the fluctuation power (magnetic, velocity, or other) measured near the ion scales in the solar wind is generated by instabilities, rather than driven by the turbulent cascade?

Figure 14 shows the probability distribution (see the yellow histogram) of parallel ion beta β _∥, using the Wind dataset described in Bale et al. (2009). The colored lines show the cumulative distribution of “unstable” measurements, i.e. data points around and beyond the theoretical instability thresholds indicated in Fig. 13 by dotted lines. The black line gives the sum of all colored histograms. For solar wind intervals with β _∥≥ ∼3, more than 20 % of the intervals would be unstable. However, the magnetic field fluctuation measurements, shown in Fig. 13, suggest that the power is enhanced well before the thresholds—hence the effect may be much larger.

Fig. 14

Probability distribution of parallel ion beta β _∥ in the data set analyzed by Bale et al. (2009). The total distribution is shown in yellow; the most probable value of β _|| in the solar wind is around 0.8. The various colored lines show the normalized histograms of occurrence of data at and beyond a certain threshold for different types of instabilities, as calculated by Hellinger et al. (2006), the black line gives the sum of all colored histograms: at high β _∥, more than 20 % of the solar wind is unstable

It seems that the magnetic and velocity fluctuation power is injected near the ion scales by instabilities, whose energy source is solar wind expansion or compression, and that this effect is dependent on the plasma β. These quasi-linear ion instabilities co-exist with the non-linear turbulent cascade in the solar wind. Therefore, if the goal is to study cascade physics, care must be taken when studying ion scale fluctuations, to be certain that the plasma is very near to isotropic T _⊥/T _||∼1 to avoid the quasi-linear ion instabilities. Interestingly, the bottom panel of Fig. 13, which shows the collisional age of protons,¹⁶ demonstrates that the condition T _⊥/T _||∼1 corresponds to a solar wind plasma that is collisionally well-processed (‘old’) and so remains ‘fluid-like’, rather than kinetic. The measurements of ‘kinetic’ turbulence must be qualified by considering the particle pressure anisotropies, and relative drifts between protons and α-particles and protons and electrons (Chen et al. 2013b; Perrone et al. 2013).

3.3 Small Scale Inertial Range Between Ion and Electron Scales, and Dissipation at Electron Scales

As far as the turbulent cascade crosses the ion scales and before reaching the electron scales (the satellite frequencies being 3≤f≤30 Hz), magnetic spectra follow $\sim k_{\perp}^{-2.8}$ (Alexandrova et al. 2009; Chen et al. 2010a; Sahraoui et al. 2010), see Fig. 9. This spectral shape seems to be independent of the local plasma parameters, as far as the angle between the flow and the field θ _BV is quasi-perpendicular (Alexandrova et al. 2009, 2012).

The electron density spectrum between ion and electron scales was determined by Chen et al. (2012a, 2013a) using the high frequency measurements of spacecraft potential on ARTEMIS. Figure 15 shows 17 electron density spectra normalized to the ion gyroradius, measured for θ _BV >45^∘ in the solar wind. At large scales, the spectra are in agreement with previous observations (see Fig. 3). At small scales, for kρ _i ≥3 the electron density spectra follow the ∼k ^−2.75 power-law, which is close to the typical value of –2.8 found in the magnetic field spectrum.

Fig. 15

17 electron density spectra normalized in scale to the ion gyroradius, showing a flattening at ion scales ∼(kρ _i )⁻¹, as in Fig. 3, and a slope close to –2.75 between ion and electron scales Chen et al. (2013a) in agreement with the magnetic spectrum at these scales, see Fig. 9

The observations of well defined power-laws in magnetic and density spectra between ion and electron scales suggest that at these scales there is a small scale inertial range (Alexandrova et al. 2007, 2008, 2009; Kiyani et al. 2009; Chen et al. 2010a, 2012a; Sahraoui et al. 2010) or an electron inertial range (Smith et al. 2012).

Kolmogorov arguments for Electron MHD lead to a ∼k ^−7/3 magnetic energy spectrum (Biskamp et al. 1996, 1999; Cho and Lazarian 2004). More recent theories of strong KAW turbulence also predict a –7/3 spectrum for both density and magnetic field (Schekochihin et al. 2009). The fact that the observed spectra are typically steeper than this has been explained in several ways, including electron Landau damping (Howes et al. 2011b), compressibility effect (Alexandrova et al. 2007) and an intermittency correction resulting in a spectral index of –8/3 (Boldyrev and Perez 2012). The same spectral index of −8/3 can be also obtained in quasi-bidimentional strong Electron MHD turbulence (k _⊥≫k _∥) when parallel cascade is weak (Galtier et al. 2005). A model of Rudakov et al. (2011) of KAW turbulence with nonlinear scattering of waves by plasma particles gives spectral index between 2 and 3.

As we have mentioned, the magnetic and density spectra of Figs. 9 and 15 are measured for quasi-perpendicular θ _BV . Varying this angle, one may resolve turbulent fluctuations with different ${\bf k}$, as discussed in Sect. 2.1. Chen et al. (2010a) used a multi-spacecraft technique to measure the wavevector anisotropy of the turbulence between ion and electron scales (up to ∼10 Hz) using two-point structure functions. They found the turbulence to be anisotropic in the same sense as in the MHD scale cascade, with k _⊥>k _∥, corresponding to “eddies” elongated along the local mean field direction (Fig. 16, left). They also found the spectral index of the perpendicular magnetic fluctuations δB _⊥ to become steeper for small θ _B (the angle between ${\bf B}$ and the separation vector between Cluster satellites), i.e. for ${\bf k}$ parallel to ${\bf B}$ (Fig. 16, right), suggestive of strong whistler or kinetic Alfvén turbulence (Cho and Lazarian 2004; Schekochihin et al. 2009; Chen et al. 2010b; Boldyrev and Perez 2012). Note that two-point structure functions cannot resolve spectral indices steeper than −3, e.g. Abry et al. (1995, 2009), Chen et al. (2010a). So, it is possible that the parallel spectral index of δB _⊥ is steeper than what is shown in Fig. 16 (right).

Fig. 16

(Left) Power in δB _⊥ (in color) as a function of parallel and perpendicular scale between ion and electron scales (Chen et al. 2010a). (Right) Spectral index as a function of angle θ _B (the angle between ${\bf B}$ and the separation vector between Cluster satellites) for the perpendicular δB _⊥ and parallel δB _∥ field components (Chen et al. 2010a)

Recently, Turner et al. (2011) studied anisotropy of the magnetic fluctuations up to ∼20 Hz. The authors used the reference frame based on the mean magnetic field and velocity, which allow to check the axisymmetry and importance of the Doppler shift for k _⊥ fluctuations (Bieber et al. 1996). The authors found that the spectrum of magnetic fluctuations in the direction perpendicular to the velocity vector in the plane perpendicular to ${\bf B}$, ${\bf V}_{sw\perp}$, is higher than the spectrum of δB along ${\bf V}_{sw\perp}$. This is consistent with a turbulence with k _⊥≫k _∥, where the fluctuations with ${\bf k}$ along ${\bf V}_{sw\perp}$ are more affected by the Doppler shift than the fluctuations with ${\bf k}$ perpendicular to ${\bf V}_{sw\perp}$. These results are also in agreement with the magnetosheath observations between ion and electron scales (Alexandrova et al. 2008).

What happens at smaller scales? Several authors have suggested that the electromagnetic turbulent cascade in the solar wind dissipates at electron scales. These scales are usually called electron dissipation range, e.g. Smith et al. (2012).

Figure 17 is reproduced from Alexandrova et al. (2012). The upper panel shows a number of magnetic field spectra measured under different plasma conditions: 100 spectra from ion scales to a fraction of electron scales, and 7 spectra measured from the MHD range to a fraction of electron scales. At scales smaller than the ion scales (k _⊥>k _ρi ,k _λi ), all the spectra can be described by one algebraic function covering electron inertial and dissipation ranges,

$$ E(k_{\perp}) = E_0 k_{\perp}^{-\alpha}\exp{(-k_{\perp}\ell_d)} $$

(6)

where α≃8/3 and where ℓ _d is found to be related to the electron Larmor radius ρ _e , with a correlation coefficient of 0.7. This law is independent of the solar wind properties, slow or fast, and of ion and electron plasma beta, indicating the universality of the turbulent cascade at electron scales. The compensated 100 spectra with the $k_{\perp}^{8/3}\exp{(k_{\perp}\rho_{e})}$–function are shown in the bottom panel of Fig. 17: they are flat over about 2 decades confirming the choice of the model function

$$ E(k_{\perp})=E_0 k_{\perp}^{-8/3} \exp(-k_{\perp}\rho_e) $$

(7)

to describe solar wind spectrum at such small scales.

Fig. 17

100 magnetic field spectra in the kinetic range to a fraction of electron scales and 7 magnetic field spectra covering fluid and kinetic scales, with spectra compensated to (k _⊥ ρ _e )^8/3exp(k _⊥ ρ _e ) in the lower panel (Alexandrova et al. 2012)

It is interesting that a similar curved spectrum is expected in the Interstellar Medium turbulence, but at ion scales (Spangler and Gwinn 1990; Haverkorn and Spangler 2013).

Another description of the spectrum within the electron inertial and dissipation ranges was proposed by Sahraoui et al. (2010). It consists of two power-laws separated by a break, see Fig. 18 (left). This double-power-law model can be formulated as

$$ \tilde{E}(k_{\perp})=A_1k_{\perp}^{-\alpha_1} \bigl(1-H(k_{\perp}-k_b)\bigr) + A_2k_{\perp}^{-\alpha_2}H(k_{\perp}-k_b), $$

(8)

H(k _⊥−k _b ) being the Heaviside function, k _b the wave number of the break, A _1,2 the amplitudes of the two power-law functions with spectral indices α _1,2 on both sides of k _b . This model has five free parameters. A statistical study of the solar wind magnetic spectra at high frequencies (f>3 Hz) shows that α ₁ does not vary a lot, α ₁=2.86±0.08 (Alexandrova et al. 2012). Then the amplitudes A ₁ and A ₂ are equal at the break point. Therefore we can fix two of the five parameters of model (8). This model has thus three free parameters, A ₁, α ₂ and k _b (in comparison with one free parameter, E ₀, in Eq. (7)).

Fig. 18

(Left) Magnetic spectrum from Sahraoui et al. (2010), compared with ∼f ^−2.8 for 4≤f≤35 Hz and with ∼f ^−3.5 for 50≤f≤120 Hz, the break frequency is around 40 Hz. (Right) A zoom on the high frequency part of the spectrum on the left, fitted with ∼f ^−2.6exp(−f/f ₀), the exponential cut-off frequency f ₀=90 Hz is close to the Doppler shifted ρ _e , $f_{0}\simeq f_{\rho _{e}}=V_{sw}/2\pi\rho_{e}$. This last fitting function is equivalent to the model (7) for wave vectors

Figure 18 (left) shows the frequency spectrum from (Sahraoui et al. 2010), compared at high frequencies¹⁷, f>3 Hz, with the double power-law model (8) with α ₁≃2.8, α ₂≃3.5 and the spectral break at f _b ≃40 Hz. Figure 18 (right) shows the total power spectral density for the same dataset fitted with the exponential model (6), which can be written for frequency spectrum as ∼f ^−αexp(−f/f ₀). The parameters of the fit are α≃8/3 and the exponential cut-off frequency f ₀=90 Hz, which is close to the Doppler shifted electron gyro-radius ρ _e for this time interval. Therefore, the model (7) can be applied in this particular case as well.

In the statistical study by Alexandrova et al. (2012), the authors concluded that model function (7) describes all observed spectra, while the double-power-law model (8) cannot describe a large part of the observed spectra. Indeed the unique determination of the spectral break k _b with A ₁=A ₂ at the break is not always possible because of the spectral curvature, and for low intensity spectra there are not enough data points to allow a good determination of α ₂.

The equivalence between the electron gyro-radius ρ _e , in the solar wind turbulence, and the dissipation scale ℓ _d , in the usual fluid turbulence, can be seen also from Fig. 19 where the Universal Kolmogorov Function E(k)ℓ _d /η ² is shown as a function of kℓ _d (Frisch 1995; Davidson 2004), for three different candidates for the dissipation scale ℓ _d , namely for ρ _i , λ _i and ρ _e ; and for one time characteristic scale, namely the electron gyro-period $f_{ce}^{-1}$. For simplicity, the kinematic viscosity η is assumed to be constant, despite the varying plasma conditions. One can see that the ρ _i and λ _i normalizations are not efficient to collapse the spectra together. Normalization on λ _e gives the same result as for λ _i . At the same time, the normalizations on ρ _e and f _ce bring the spectra close to each other, as expected while normalizing by ℓ _d . In addition to the spectral analysis presented in Fig. 17, the Universal Kolmogorov Function normalization gives an independent confirmation that the spatial scale which may play the role of the dissipation scale, in the weakly collisional solar wind, is the electron gyro-radius ρ _e .

Fig. 19

Universal Kolmogorov function ∝ℓ _d E(k) for hypothesized dissipation scales ℓ _d as a function of (a) kρ _i , (b) kλ _i , (c) kρ _e and (d) f/f _ce . Figure from Alexandrova et al. (2009), corrected for 3 STAFF-SA frequencies, as explained in Alexandrova et al. (2012)

It is important to mention, that the amplitude parameter E ₀ of the exponential model (7) is found to be related to the solar wind plasma parameters (Alexandrova et al. 2011), see Fig. 20. The amplitude of the raw frequency spectra is found to be related to the ion thermal pressure as ∼nk _B T _i (Fig. 20, upper line). This is similar to the amplitude of the inertial range spectrum, which is found to be correlated to the ion thermal speed $\sim V_{th}^{2}$ (Grappin et al. 1990). The amplitude of the k-spectra, as well as the amplitude of the normalized kρ _e -spectra, appears to depend on the ion temperature anisotropy as ∼(T _i⊥/T _i∥)^1.6±0.1 (Fig. 20, lower line). This last result suggests that the ion instabilities present around the ion break scale may indeed inject or remove energy from the cascade (see our discussion in Sect. 3.2). Therefore, the scales around the ion break (or ‘transition range’, see Fig. 9) may be seen, in part, as the energy injection scales for the small scale inertial range.

Fig. 20

(a) The 100 magnetic frequency spectra measured by Cluster/STAFF in the solar wind for f>1 Hz, analyzed in Alexandrova et al. (2012); (b) intensity of the frequency spectra at a fixed frequency f=5 Hz as a function of the ion thermal pressure nk _B T _i : dependence is P∼nk _B T _i ; (c) the same spectra as in panel (a) but shown as a function of kρ _e and superposed using an amplitude factor A (equivalent to E ₀ in Fig. 17); (d) The amplitude A as a function of the ion temperature anisotropy T _i⊥/T _i∥: dependence A∼(T _i⊥/T _i∥)^1.6±0.1 is observed. Figure from Alexandrova et al. (2011)

In usual fluid turbulence, the far dissipation range is described by E(k)∼k ³exp(−ckℓ _d ) (with c≃7) (Chen et al. 1993). The exponential tail is due to the resistive damping rate γ∝k ² valid in a collisional fluid. In the collisionless plasma of the solar wind there is no resistive damping, and thus the observation of the exponential spectrum within the electron dissipation range deserves an explanation.

Howes et al. (2011a) consider a model (“weakened cascade model”) which includes the nonlinear transfer of energy from large to small scales in Fourier space and the damping of kinetic Alfvén waves. The spectral laws are respectively $E_{k} \propto k_{\bot}^{-5/3}$ at large scales and $E_{k} \propto k_{\bot}^{-7/3}$ between ion and electron scales. The damping becomes important at electron Larmor radius ρ _e scale. It is obtained by linearizing the Vlasov-Maxwell equations in the gyrokinetic limit (k _∥≪k _⊥, with frequencies f≪f _ci ). For k _⊥ ρ _i ≫1 it has the form $\gamma\propto k_{\|}k_{\bot}^{2}$. Taking into account the assumption of critical balance τ _nl =τ _A (i.e. k _⊥ v=k _∥ V _A ) (Goldreich and Sridhar 1995), and the spectral index −7/3 (i.e. $v\sim k_{\bot}^{-2/3}$), one gets $k_{\|} \propto k_{\bot}^{1/3}$. Therefore, the damping term takes the form $\gamma\propto k_{\bot}^{2+1/3}$. The exponent of the damping rate is thus very close to the k ² scaling of the Laplacian viscous term, which is known to lead in hydrodynamical turbulence to an exponential tail in the dissipation range. Indeed, when taking into account the damping term, Howes et al. (2011a) obtain numerically a final curved tail at scales smaller than electron scales. Superficially, this spectrum thus resembles the analytic form which we have found to be valid to describe the solar wind turbulence, Eq. (7).

As we have just seen, the model of Howes et al. (2011a) assumes the k _⊥≫k _∥–anisotropy and very low frequencies f≪f _ci . Present multi-satellite observations can not cover the electron inertial and dissipation ranges at scales smaller than the smallest satellite separation ∼100 km. Only the one-satellite technique of Bieber et al. (1996) can be used. A first attempt to determine the distribution of wave-vectors ${\bf k}$ of the electromagnetic fluctuations within the electron inertial and dissipation ranges (for the observed frequencies [8,500] Hz) was carried out in the magnetosheath by Mangeney et al. (2006). They show that the wavevectors ${\bf k}$ of the electromagnetic fluctuations are distributed within the plane nearly perpendicular to the mean field ${\bf B}$, with an angle of ∼±5^∘ around this plane. However, the authors have not found any agreement between the observed properties of magnetic fluctuations and KAW turbulence.

The nature of turbulence between ion and electron scales is still under debate. As with the MHD scale cascade, there are a number of observational and theoretical works, which identify turbulent fluctuations at small scales as having properties of linear wave modes (e.g., Denskat et al. 1983; Goldstein et al. 1994; Ghosh et al. 1996; Biskamp et al. 1996, 1999; Leamon et al. 1998; Cho and Lazarian 2004; Bale et al. 2005; Galtier 2006; Sahraoui et al. 2010, 2012; Howes et al. 2006, 2008, 2012b; Schekochihin et al. 2009; Gary and Smith 2009; Chandran et al. 2009; Chen et al. 2010b, 2013a; Salem et al. 2012; Klein et al. 2012; Boldyrev and Perez 2012). A recent analysis by Chen et al. (2013c) showed that the ratio of density to magnetic fluctuations in the range between ion and electron scales is very close to that expected for kinetic Alfvén waves, and not whistler waves, and concluded that the fluctuations in this range are predominantly strong kinetic Alfvén turbulence. The precise interplay between linear and non-linear physics is an important unsolved problem in plasma turbulence.

Solar wind observations and numerical simulations show that the fluctuations at kinetic scales have non-Gaussian distributions, indicating the presence of intermittency (Alexandrova et al. 2007, 2008; Kiyani et al. 2009; Wan et al. 2012; Wu et al. 2013). Recently, small scale coherent current sheets have been identified at scales close to electron scales (Perri et al. 2012). These features are consistent with strong, rather than weak (or wave) turbulence. The properties of the intermittency at small scales are not clear at the moment. There are two contradictory observations: (i) Alexandrova et al. (2008) show a scale dependent deviation from Gaussianity of the PDFs of the magnetic fluctuations δB _R (along the solar wind flow); (ii) Kiyani et al. (2009) show observations suggesting a scale-invariance within the small scales. Further work is needed to understand this discrepancy.

4 Discussion

In this paper we have discussed solar wind turbulence observations in a large range of scales: from the MHD scales to the electron characteristic scales.

At MHD scales, within the inertial range, the solar wind turbulence presents several general characteristics inherent to fully developed fluid turbulence: (i) energy spectra of different plasma parameters have well-defined power-laws; (ii) the probability distribution functions deviate from a Gaussian distribution, indicating stronger gradients at smaller scales (intermittency); (iii) the third order moments of turbulent fluctuations have the linear dependence on scale (the proportionality coefficient giving the energy transfer rate). The anisotropy of turbulence with respect to a mean magnetic field is shown to be important: the turbulence develops mostly in the plane perpendicular to ${\bf B}$, i.e. with k _⊥≫k _∥. The perpendicular magnetic spectrum follows $\sim k_{\perp}^{-5/3}$ scaling, while the parallel spectrum is steeper $\sim k_{\|}^{-2}$. The dominant fluctuations are Alfvénic in nature, i.e. δB _⊥>δB _∥, however, the velocity spectrum has a spectral slope of −3/2 and it does not follow the magnetic spectrum. There is a small fraction of the turbulent energy in compressible fluctuations. It is not clear whether they behave as a passive contaminant as in compressible neutral fluid turbulence or they are an active component of the turbulence in the solar wind. In other words, is it possible to describe these compressible fluctuations independently of the dominant Alfvénic cascade, or are they inherently coupled? This question is a matter of debate.

The MHD inertial range ends at ion characteristic scales. Here, different kinetic effects may take place and inject or remove energy from the turbulent cascade. In particular, the large scale energy reservoir related to the solar wind spherical expansion may be released into fluctuations, throughout instabilities, like mirror and oblique firehose instabilities, which becomes important for high ion betas (β _i >3). Then these fluctuations may interact with particles and dissipate, or participate to the turbulent cascade at smaller scales. At lower beta, the plasma is stable and more or less isotropic: no additional energy is expected to arrive to the turbulent cascade. However, the exact energy partition between fluid and kinetic degrees of freedom at ion scales is still under debate. Around ion scales magnetic spectra are variable, and the compressibility increases. A spectral break seems to appear at the ion inertial scale, suggesting that dispersive effects (Hall effect) become significant.

Between ion and electron scales, a small scale turbulent cascade seems to be established. This cascade is characterized by a k _⊥≫k _∥ anisotropy, as the MHD cascade. The k _⊥ magnetic and density spectra have a power-law shape with ≃−2.8 spectral index. Fluctuations are more compressible than within the MHD inertial range and this compressibility seems to depend on the local plasma parameters, like the plasma β. Magnetic fluctuations are non-Gaussian, indicating the presence of the intermittency.

Approaching electron scales, the fluctuations are no more self-similar: the spectrum is no more a power-law, but an exponential cut-off is observed indicating an onset of dissipation. The dissipation range spectrum is observed to have a general shape. One algebraic function $\sim k_{\perp}^{-8/3}\exp(-k_{\perp}\rho_{e})$ describes well the whole spectrum covering the small scale inertial range and the dissipation range.

The nature of the small scale cascade between ion and electron scales and the dissipation mechanism at electron scales are still under debate. The model of Howes et al. (2011a) can describe the observed exponential cut-off. The dissipation mechanism in this model is based on a quasi-linear description of the Landau damping of kinetic Alfvén waves onto electrons. Whether such description can apply on the solar wind observations is however under debate because of the presence of a significant degree of intermittency at kinetic scales.

To build a realistic model of the dissipation in the solar wind we need still to resolve an open question on the nature of the turbulent fluctuations: is it a mixture of linear waves or is it a strong turbulence with dissipation restricted to intermittent coherent structures? What is the topology of these structures—current sheets, shocks, solitons or coherent vortices?