1 Introduction

The underlying cause of coronal heating is a long-standing problem whose solution continues to elude the scientific community. In theory it should be a simple matter to account for the 0.01 % of solar output that is required to sustain the corona. However, in reality, the Sun is a very dynamic and complicated stellar object, which makes the task more difficult than first thought. A comprehensive understanding of the multitude of solar phenomena, and the movement of energy that comes with them, is essential for solving the problem.

Coronal loops are one such phenomenon, linking the photosphere to the corona, potentially providing a conduit for the energy of the solar interior to reach the atmosphere. Extensive overviews of coronal loops are given by Bray et al. (1991), with Reale (2014) specifically addressing them as bright structures confining plasma, while insight into their structure is given by Peter et al. (2013). Reale et al. (2000) presented detailed modelling of a coronal loop that was found to be impulsively heated.

Small bursts of energy of around \(10^{24}~\mbox{erg}\), called nanoflares, are potential candidates for the source of coronal heating, as originally proposed by Parker (1988). Originally referring solely to energy release through magnetic reconnection, the term nanoflare now encompasses any impulsive mechanism that delivers energy in that range, for example, heating by Alfvén waves (Moriyasu et al. 2004). The latter has yet to be confirmed despite studies of the frequency distribution of thermal energies for hard X-ray flares (Crosby, Aschwanden, and Dennis 1993), active region transient brightenings (Shimizu 1995), and quiet-Sun nanoflares and microflares (Krucker and Benz 1998; Parnell and Jupp 2000; Aschwanden et al. 2000; Benz and Krucker 2002; Aschwanden and Parnell 2002; Taroyan, Erdélyi, and Bradshaw 2011). However, it remains an open avenue of investigation.

As with any phenomenon that involves energy release, explosive events are also of interest to those investigating heating. Explosive events are defined by their non-Gaussian line profiles and short-lived nature. Since their discovery by Brueckner and Bartoe (1983), they have been the focus of numerous studies. Dere et al. (1991) used explosive events to examine magnetic reconnection by assuming that they are all the result of reconnection. Innes and Tóth (1999) conducted simulations of explosive events to examine the behaviour of temperature emission lines from reconnection. Winebarger et al. (2002) explored the energetics of explosive events and found that individual events were not energetically significant with regard to coronal and chromospheric heating. Teriaca, Madjarska, and Doyle (2002) analysed spectral lines to determine whether or not transition region explosive events have coronal counterparts. Teriaca et al. (2004) found cases where supersonic flows in small loops were associated with non-Gaussian line profiles. More recently, Madjarska, Doyle, and de Pontieu (2009) have demonstrated that explosive events and other transient phenomena may be the same processes, but observed in different ways.

The differences between non-equilibrium ionisation and local thermodynamic equilibrium modelling have been known for some time, with Mariska et al. (1982) finding substantial differences in relative ionic abundances of the quiet Sun. Müller, Hansteen, and Peter (2003) investigated the effects of non-equilibrium ionisation on condensation in transition region spectral lines. Bradshaw and Cargill (2006) found significant departure from equilibrium in models of coronal loops heated by nanoflares. In this work we factor in the effects of non-equilibrium ionisation by using the established HYDRAD code (Bradshaw and Cargill 2013) for our simulations and modelling.

In the following work we investigate a pair of brightenings reported by Innes and Teriaca (2013) that are believed to have occurred in a loop. Hydrodynamic simulations combined with forward modelling allow us to replicate the observations and suggest physical parameters such as density, loop temperature, loop length, and heating rate. The initial brightening represents a nanoflare that subsequently caused the second brightening through a heating pulse in the loop. This is supported by the results of Winebarger et al. (2013), who found that cool dense loops were impulsively heated by nanoflares.

2 Observations

A pair of explosive events were observed by Innes and Teriaca (2013) using the Solar Ultraviolet Measurements of Emitted Radiation (SUMER) spectrometer (Wilhelm et al. 1995), and then co-aligned with corresponding data from the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012). Both explosive events were associated with small-scale brightenings in the AIA data. There was a delay of 60 s between the AIA brightenings at the two sites, and each brightening coincided with an explosive event. The authors therefore concluded the likely cause to be a brightening that released energy at a loop footpoint and drove a flow along to the other footpoint where the second brightening took place. There was a delay between the two explosive events seen by SUMER, but due to the 60 s exposure time, the exact length of time could not be determined. It is reasonable to assume, however, that the delay is similar to the delay between the two brightening peaks. Because of the long exposure time used for the SUMER data, we only make use of the AIA data due to the short-lived nature of the events.

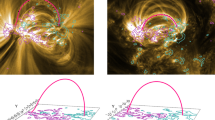
Additional evidence for the involvement of a loop is shown by Figure 1, where the two sites of the brightenings are connected by a band of increased emission shortly after the appearance of both sites. By considering the Sun to be flat in the relatively small area covered and using basic geometry, it is possible to obtain a simple approximation for the length of the loop. Earlier observations indicate that the loop is not observed before the two brightenings appear.

Figure 1
figure 1

Excerpt of the observational AIA intensity data for the 131 Å channel in the top row and the 193 Å channel in the bottom row. The images from the first column are approximately from the same time, the second column shows images obtained 70 seconds later. The axes indicate solar coordinates in arcseconds, and the pixels are squares of side length \(0.6^{\prime\prime}\). The colour of the pixels indicates the intensity, with white being the most intense. The red boxes indicate the nine pixels that correspond to the explosive events at each footpoint that are summed to produce the observational intensity plots (Figure 2).

Full size image

Sets of AIA data were plotted onto intensity maps with a pixel size of \(0.6^{\prime\prime}\) (Figure 1). A square of three by three pixels centred on each footpoint was summed and divided by the duration of the observations to create plots of intensity in units of DN against time in seconds (Figure 2). The intensity between the footpoints was also examined, but we did not believe that it accurately represented the loop structure, therefore we did not analyse it here. The discrepancy may be due to the greater column depth of material making up the observations at the footpoints compared to the middle of the loop, resulting in more background contamination of the intensity in the middle. This was carried out for the 304 Å, 171 Å, 193 Å, and the 131 Å extreme ultraviolet channels. While the event was also visible in the 211 Å channel, the emission was weak. Therefore it was not included in our analysis as presented, but it was found to be modelled as successfully as the other channels. We note that the 12 s cadence of the AIA data means that the true peaks of the intensity data may not have been observed. An improved cadence could have resulted in a better or poorer agreement with the results of our forward modelling, but our aim was to be consistent with the available data.

Figure 2
figure 2

Observational AIA intensity data for the four spectral channels showing the first (a) and second footpoint (b).

Full size image

3 Numerical Simulations

The evolution of the impulsively heated loop was simulated using the 1D hydrodynamics and radiation code HYDRAD (Bradshaw and Mason, 2003a, 2003b; Bradshaw and Cargill 2013). The loop begins in an initial idealised equilibrium where the hydrostatic equations are solved from the footpoint to the loop apex for one side and mirrored on the basis of symmetry. The equilibrium is found by time-independent uniform heating. The loop then evolved over time to ensure its stability. Then a heating pulse was injected into one of the footpoints at the top of the chromosphere, and its evolution was computed until the loop settled back into a static state. The temporal profile of the heating pulse consists of a linear increase to the peak volumetric heating rate, followed by a plateau, followed by a linear decrease to zero. The code features an adaptive mesh that allows it to maintain an accurate high-resolution representation of the transition region during these periods of heating (Taroyan and Erdélyi 2009). In this work, the resolution was such that the smallest grid cell width was 0.12 km. Bradshaw and Cargill (2013) and others found that an inadequate resolution of the transition region primarily leads to an underestimated coronal density.

The conservative form of the hydrodynamic equations and a detailed ionisation balance equation for each ion are solved by the code

$$\begin{aligned} \frac{{\partial}\rho}{{\partial}t} + \frac{\partial}{{\partial }s}(\rho \upsilon) =& 0, \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial}{{\partial}t}(\rho\upsilon) + \frac{\partial }{{\partial }s}\bigl(\rho \upsilon^{2}\bigr) =& {\rho}g_{\parallel}- \frac{{\partial }P}{{\partial }s} + F, \end{aligned}$$
(2)
$$\begin{aligned} \frac{{\partial}E}{{\partial}t} + \frac{\partial}{{\partial }s}\bigl[(E+P)\upsilon\bigr] =& {\rho \upsilon}g_{\parallel}+ \frac{\partial }{{\partial}s} \biggl({\kappa}T^{5/2} \frac{{\partial}T}{{\partial }s} \biggr) + E_{\mathrm{H}}(s,t) - E_{\mathrm{R}}(s,t), \end{aligned}$$
(3)
$$\begin{aligned} E =& \frac{1}{2}\rho\upsilon^{2} + 3k_{\mathrm{B}}nT, \end{aligned}$$
(4)
$$\begin{aligned} P =& 2k_{\mathrm{B}}nT, \end{aligned}$$
(5)
$$\begin{aligned} \frac{{\partial}Y_{i}}{{\partial}t} + \frac{\partial}{{\partial }s}(Y_{i}\upsilon) =& n(I_{i-1}Y_{i-1} + R_{i}Y_{i+1} - I_{i}Y_{i} - R_{i-1}Y_{i}). \end{aligned}$$
(6)

\(\rho\) denotes the mass density; \(\upsilon\) the bulk velocity; \(P\) the total pressure; \(T\) the temperature; \(g_{\parallel}\) the gravitational acceleration parallel to the magnetic field; \(k_{\mathrm{B}}\) the Boltzmann constant; \(\kappa\) the coefficient of thermal conductivity; \(E_{\mathrm{H}}\) the volumetric heating rate consisting of time-independent uniform heating and a time-dependent impulsive heating rate; \(E_{\mathrm{R}}\) the radiative energy loss rate, which assumes optically thin emission and a fully ionised plasma as a function of \(s\) and \(t\), accounting for the non-equilibrium state of the ions; \(Y_{i}\) the fractional population, normalised to 1, of ion stage \(i\) of element \(Y\); \(I_{i}\) and \(R_{i}\) are the ionisation and recombination rates from/to ion stage \(i\); \(n\) is the electron number density; and \(F\) is a forcing term that drives cold plasma injection. We note that the second term of the energy equation (4) is the sum of the electron and ion thermal energies. In addition, the forcing term is zero for impulsive heating, and the time-dependent impulsive heating rate is zero for cold plasma injection.

The simulations were carried out with the fifteen most abundant elements in the solar atmosphere taken to be in equilibrium when generating the initial conditions. However, they were considered to be in non-equilibrium for the ensuing simulation to paint a realistic picture of the loop evolution because the assumption that the ion population remains in equilibrium does not hold once the heating pulse is introduced to the stable loop. Borrini and Noci (1982) reported considerable deviation from equilibrium in loops characterised by high-speed flows, especially in cold loops, as a result of the greater temperature and density gradients involved. Bradshaw (2009) concluded that rapid heating can still result in a lack of equilibrium even at high densities around \(10^{10}~\mbox{cm}^{-3}\), although the differences decrease with increasing density. It is therefore possible that ionisation may be close to equilibrium in our case, but simulating under non-equilibrium ionisation is still favourable. Our forward modelling relies heavily on the emission from the ions, so if they were to be erroneously distributed within the loop, the accuracy of the models would suffer.

For simplicity, the loop was assumed to have zero inclination such that it was perpendicular to the solar surface. The approximate coordinates in arcseconds of the observed loop footpoints are −193, −140 for the first (northern) and −191, −146 for the second (southern) footpoint. The ends of the loop were rooted in a chromosphere of temperature \(2\times 10^{4}~\mbox{K}\). The other parameters were varied through a process of trial and error in an effort to determine their value.

4 Forward Modelling

The physical data generated by the simulations were fed into the forward-modelling component of HYDRAD, which combined it with instrumental response functions for the four AIA channels to generate intensity in units of \(\mbox{DN}\,\mbox{s}^{-1}\,\mbox{pixel}^{-1}\) by

$$ I(\lambda,n,T) = \frac{0.83{\times}G(\lambda){\times}\mathrm{Ab}(Y){\times }{Y_{i}}{\times}\epsilon(\lambda,n,T){\times}{\langle}\mathrm{EM}{\rangle }}{4\pi \times(\frac{hc}{\lambda})}. $$
(7)

\(G(\lambda)\) denotes the instrumental response function in \(\mbox{DN}\,\mbox{pixel}^{-1}\,\mbox{photon}^{-1}\,\mbox{sr}\,\mbox{cm}^{2}\); \(\frac{hc}{\lambda}\) the photon energy in erg; 0.83 the ratio of protons to electrons; \(\mathrm{Ab}(Y)\) the abundance of element \(Y\) relative to hydrogen; \(Y_{i}\) the population fraction of charge state \(i\) of element \(Y\); \(\epsilon(\lambda,n,T)\) the emissivity of the line in \(\mbox{erg}\,\mbox{s}^{-1}\,\mbox{cm}^{3}\); and \({\langle }\mathrm{EM}{\rangle}\) the spatially averaged column emission measure in the pixel, in units of \(\mbox{cm}^{-5}\). We used the same response functions as Bradshaw and Klimchuk (2011); these functions are a product of the plate scale, effective area, and gain of the AIA instrument.

Intensity plots corresponding to Figure 2 were created from the numerical results by forward modelling. The emission might be optically thick in the 304 Å channel, therefore the modelled intensity may be inaccurate for this channel because the code does not include optically thick emission. However, the use of multiple other channels minimises any effects of this. To create synthetic observations that could be compared to the observed intensities, the loop was projected onto a flat base and was regridded to the AIA pixel size to account for the geometry (Figure 3). Then the data points in a corresponding three-pixel length of loop were summed to create the synthetic intensity. The location of this loop section was varied to find the best observational match.

Figure 3
figure 3

Two observers are shown, highlighting how the line-of-sight depth through the loop increases closer to the footpoints when using arbitrarily equally spaced portions. Not to scale.

Full size image

5 Results and Discussion

We went through a cyclic process of trial and error whereby the results of the forward modelling were compared to the observations to inform the choice of parameters for a new set of simulations in an attempt to approach the observed values. The final results yielded a footpoint density of \(1.2\times10^{10}~\mbox{cm}^{-3}\), which resulted in a loop peak temperature of \(4\times10^{5}~\mbox{K}\) before any heating. The temperature of the loop was derived from the footpoint density and not chosen independently. The uniform background heating rate was \(1.68\times10^{-4}~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\). The heating event of the loop had a maximum impulsive heating rate of \(0.08~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\) and a scale length of \(1\times10^{5}~\mbox{m}\). The heating pulse was applied to the top of the chromosphere at the first footpoint because the observations show the first footpoint to peak in intensity before the second footpoint.

It was found that as the total duration of the heating event increased, the intensity peaks broadened, and secondary peaks to the right became more pronounced. A duration of 50 s was found to give the best match to the observations, which is comparable to the peak width at the first footpoint shown in Figure 2. This was split between the three parts of the pulse’s temporal profile as 20 s for the linear increase, 10 s for the plateau, and 20 s for the linear decrease. The similarities between the observed pulse width and the simulated heating duration provides support for the proposed scenario.

The evolution of the impulsively heated loop can be seen in the hydrodynamic data in Figure 4. The initial state is clearly shown with almost symmetric density and temperature profiles before the heating event. The influx of energy approximately triples the temperature of the loop near to its first footpoint and significantly heats the nearby chromosphere, triggering an evaporation of material. The hot material flows into the loop, causing an increase in density and temperature as it travels to the other end. The flow rebounds and travels back along the loop, most clearly seen by the velocity, but with much less energy, having imparted much of it to the chromosphere at the second footpoint during the rebound.

Figure 4
figure 4

Simulated hydrodynamic parameters of the dynamically heated loop used in the final result. All plots are in a field of the loop coordinate (Mm) against time (s), with (a) showing temperature (K), (b) showing velocity (\(\mbox{cm}\,\mbox{s}^{-1}\)), with red indicating positive velocity in the increasing loop coordinate direction, and (c) showing base 10 logarithmic density (\(\mbox{cm}^{-3}\)).

Full size image

After 240 simulations we found that a loop heated to a peak of \(5.8\times10^{5}~\mbox{K}\) from an initial temperature of \(4\times10^{5}~\mbox{K}\) (Figure 5) had emission lines that matched the ordering of the spectral lines observed (Figure 2). For example, the 304 Å line peaks first, followed by the three others peaking shortly after each other, and the positioning of the peaks relative to each other is approximately consistent with the observations. The loop was taken to be 10.2 Mm long, including 1 Mm of chromosphere at each end, to match the observed 60-second delay between peak intensities, which was found to decrease with shorter lengths and increase with longer lengths. For example, a previous loop with a length of 9 Mm had a delay of 50 seconds between the peaks.

Figure 5
figure 5

Forward-modelled intensity for the impulsively heated loop showing the first footpoint (a) and the second footpoint (b). The heating event lasted for 50 seconds and had a maximum heating rate of \(0.08~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\). It had a scale length of \(1\times10^{5}~\mbox{m}\) and was injected 1 Mm into the loop, at the top of the chromosphere.

Full size image

With the loop length and peak separation known, it is possible to derive the propagation speed of the heating pulse from the intensity plot. Using the distance in loop coordinates between parts of the summed loop sections at each footpoint, the outer edges, the centres, and the inner edges, a distance-over-time calculation is possible. We took the average of the three values, with the edges being the upper and lower error bounds. This yielded a propagation speed of \(100\pm37~\mbox{km}\,\mbox{s}^{-1}\). By combining the known 60-second delay between the brightenings with simple geometry and the observed image (Figure 1), it is possible to obtain an approximate propagation speed of \(102\pm15~\mbox{km}\,\mbox{s}^{-1}\). This is done by calculating the length of a semi-circle connecting the centre pixels of the red boxes, and the length of one connecting the two outermost pixels. These two lengths give us our upper and lower bounds, with the average yielding the stated value. The approximate observed propagation speed agrees well with the simulated value. We found that higher temperatures resulted in higher propagation speeds and that greater heating rates increased the maximum velocity in the loop.

Loops with a higher initial apex temperature, and therefore density, resulted in an intensity that was seen to drop during the pulse for some AIA channels. However, where the initial temperature was too low, the 304 Å line dominated the profiles for all of the heating pulses we studied. Higher temperatures in general yielded intensities that were orders of magnitude greater than those observed and had more jagged lines. Where the initial temperature was low enough to allow for pulses to cause increases in intensity, the pulses with higher heating rates tended to favour the 171 Å line. It deviated significantly from the other three lines and made a second peak more pronounced. For comparison we include Figure 6, where the parameters are identical to those of Figure 5, except for a ten times increase in footpoint density that yields an initial apex temperature of \(8.7\times10^{5}~\mbox{K}\). The higher temperature results in initial intensities almost two orders of magnitude above the observed values.

Figure 6
figure 6

Forward-modelled intensity for an impulsively heated loop showing the first footpoint (a) and the second footpoint (b). The parameters are identical to those of the final impulsively heated loop (Figure 5) except for a ten times increase in footpoint density. The heating event lasted for 50 seconds and had a maximum heating rate of \(0.08~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\). It had a scale length of \(1\times10^{5}~\mbox{m}\) and was injected 1 Mm into the loop, at the top of the chromosphere.

Full size image

The intensity of the first footpoint tended to be increasingly favoured over the second in the case of high pulse scale lengths, in contrast to the observations where the second footpoint has greater intensity. This effect at the first footpoint is because higher scale lengths lead to a greater column depth of material being at a higher temperature, so the intensity increases commensurately. The scale length was subsequently set at \(1\times10^{5}~\mbox{m}\) which yielded footpoints with more comparable intensities.

The success in reproducing the appearance of the line profiles with this pulse leads us to believe there were other contributions from the Sun, which were not taken into account by our model. These probably caused the second footpoint to have greater intensity in the observations. This position is supported by the fluctuations seen in the observations before the pulse begins. They suggest another source, independent from the heating event, of temperature variance or intensity. Another possibility is that the loop may not be symmetrical about the apex, which could lead to different density stratifications for the two ends, which in turn may lead to a higher intensity for the second footpoint.

Originally, the loops had peak intensities several times greater than the observed values. An effort was made to reduce these because the overall shape of the line profiles agreed well. By reducing the width of the loops in the forward model to 2 Mm, the intensities across the loops were reduced by a proportional amount to be more reasonable (Figure 5). However, this also reduced the initial intensities before the pulse, which were below target to begin with. To mitigate this, we attributed the initial intensity from the observations to unresolved background emission and added an appropriate number to all points in each channel to make the first points comparable to their observed counterparts. This reduced the peaks and improved the initial intensities (Figure 7).

Figure 7
figure 7

Forward-modelled intensity for the dynamically heated loop (Figure 5) plus background addition, showing the first footpoint (a) and the second footpoint (b). The heating event lasted for 50 seconds and had a maximum heating rate of \(0.08~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\). It had a scale length of \(1\times10^{5}~\mbox{m}\) and was injected 1 Mm into the loop, at the top of the chromosphere.

Full size image

The equations governing the heating pulse were integrated in time and space along the loop to determine the total amount of energy deposited by the event. The integral took the form of

$$ E_{\mathrm{p}} = E_{0} \int_{0}^{L} \mathrm{e}^{-\frac{(s-s_{0})^{2}}{2(s_{\mathrm{H}})^{2}}}\,\mathrm{d}s \biggl\{ \int_{t_{0}}^{t_{1}} \frac{(t-t_{0})}{(t_{1}-t_{0})}\,\mathrm{d}t + \int_{t_{1}}^{t_{2}} \mathrm{d}t + \int _{t_{2}}^{t_{3}} \biggl[ 1 - \frac{(t-t_{2})}{(t_{3}-t_{2})} \biggr] \,\mathrm{d}t \biggr\} , $$
(8)

where \(E_{\mathrm{p}}\) denotes the total heating energy per unit area due to the pulse, \(E_{0}\) the impulsive heating rate, \(L\) the length of the loop, \(s\) the loop position, \(s_{0}\) the heating location, \(s_{\mathrm{H}}\) the heating scale length, \(t\) the time, \(t_{0}\) the time the heating rise phase begins, \(t_{1}\) the time the heating rise phase ends, \(t_{2}\) the time the heating decay phase begins, and \(t_{3}\) the time the heating decay phase ends. This was solved by using a standard definite integral

$$ \int_{0}^{u} \mathrm{e}^{-x^{2}}\,\mathrm{d}x = \frac{\sqrt{\pi}}{2}\mathrm{erf}(u), $$
(9)

where erf is the error function. The calculation, using our circular cross-sectional area of \(3.14\times10^{16}~\mbox{cm}^{2}\), yielded a total heating energy of \(1.89\times10^{24}~\mbox{erg}\), which is consistent with the energy of a nanoflare (Parker 1988).

In an effort to improve on this result, we tried to recreate the observations with an injection of cold plasma instead of with a heating pulse. For this the forcing term from the momentum equation (2) that had not existed up until this point took the following form:

$$ F = A{\rho} {\sin} \biggl(\frac{t-t_{o}}{t_{\mathrm{d}}}\pi \biggr){\cos} \biggl( \frac {s-s_{0}}{2s_{\mathrm{H}}}\pi \biggr), $$
(10)

where \(A\) is the acceleration of the plasma, \(t_{0}\) the injection start time, \(t_{\mathrm{d}}\) the duration, \(s_{0}\) the location, and \(s_{\mathrm{H}}\) is the scale length. The best results were achieved where the physical parameters were the same as used for the most accurate impulsively heated loop.

The physical evolution of the loop is shown in Figure 8, with an initial state identical to that of Figure 4. The cold plasma is shown by the temperature plot to extend the black chromosphere up into the loop. The density plot for the same region indicates a peak of high density moving with the footpoint until the plasma injection ceases and it falls back as a result of gravity. While the bulk of the material was contained in this peak, there was also a much smaller pulse of density that traversed the loop similarly to the impulsive heating case. This caused the same effects as seen previously, with all three plots indicating a flow of material from the first footpoint to the second footpoint and then back again. The second footpoint is fairly similar to the one shown in Figure 4. In this instance, the pulse duration was 60 s, the scale length was \(5\times10^{5}~\mbox{m}\), and the acceleration was \(6\times10^{5}~\mbox{cm}\,\mbox{s}^{-2}\).

Figure 8
figure 8

Simulated hydrodynamic parameters for the best loop from the cold plasma injection efforts. All plots are in a field of the loop coordinate (Mm) against time (s), with (a) showing temperature (K), (b) showing velocity (\(\mbox{cm}\,\mbox{s}^{-1}\)) with red indicating positive velocity in the increasing loop coordinate direction, and (c) showing base 10 logarithmic density (\(\mbox{cm}^{-3}\)).

Full size image

The propagation speed was determined in the same manner as before from the intensity plot, yielding a value of \(87\pm 33~\mbox{km}\,\mbox{s}^{-1}\). While the error bounds overlap with those of the observed speed, it is less comparable than the value derived from the impulsive heating simulations.

The loop reached a peak temperature of \(5.1\times10^{5}~\mbox{K}\) and was found after 14 simulations to yield the most accurate intensity plot of the cold plasma injection simulations. It had the same initial problems as the impulsively heated loop, however, and was found to be improved by the addition of background values in the same manner (Figure 9).

Figure 9
figure 9

Forward-modelled intensity for the loop subjected to cold plasma injection plus background addition, showing the first footpoint (a) and the second footpoint (b). The plasma injection lasted for 60 seconds and had an acceleration of \(6\times10^{5}~\mbox{cm}\,\mbox{s}^{-2}\). It had a scale length of \(5\times10^{5}~\mbox{m}\) and was injected 1 Mm into the loop, at the top of the chromosphere.

Full size image

6 Summary and Conclusions

We used hydrodynamic simulations and forward modelling to recreate the intensity profile of a loop event observed by AIA. The initial conditions assumed the fifteen most abundant solar elements to be in equilibrium, and the loop was kept stable by time-independent uniform heating. During the simulations the elements were considered as not in equilibrium, and a single heating pulse was injected at the first footpoint, later replaced with an injection of cold plasma. The output was fed into forward models to create synthetic intensity profiles that were compared to the observed ones.

The results depicted in Figure 7 approximately agree, but the shape and ordering of the profiles are notably affected by relatively small changes in the parameters. The addition of the background was necessary to create plots that better matched the observations. However, the observed intensity before and after the events fluctuated when we added a constant value to each channel, so the comparison is not perfect.

In Figure 9, which shows the cold plasma injection, the intensity of the second footpoint is a much better match to the observations. However, the first footpoint is noticeably worse because the cold plasma moved the temperature gradient further along the loop, so we had to move the summed loop section along as well. This caused the channels to no longer peak in the correct time order, and they had lower intensities than seen for impulsive heating.

By comparing the propagation speeds of the two methods derived from their intensity plots, we find that the value of \(100\pm 37~\mbox{km}\,\mbox{s}^{-1}\) from the impulsive heating simulations better matches the approximate observed value of \(102\pm15~\mbox{km}\,\mbox{s}^{-1}\) than the value of \(87\pm33~\mbox{km}\,\mbox{s}^{-1}\) from the cold plasma injection simulations. We conclude that the observations are better modelled by a heating pulse, similar to the findings of Reale et al. (2000), instead of an injection of cold plasma.

The resemblance between our simulated loop and the observed brightenings appears to confirm the initial suggestions by Innes and Teriaca (2013), who reported that they were studying a loop. The rebounding flow seen in Figure 4 could lend support to their theory that the second brightening is a downward and reverse jet. However, modelling the accompanying expanding ring of increased emission around the second footpoint that they observed was beyond the scope of our model here. It might be partially responsible for the greater peak intensity of the second footpoint seen in the observations.