Abstract
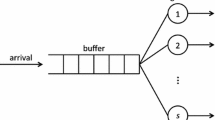
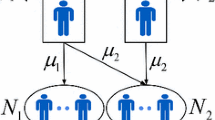
We consider the problem of staffing large-scale service systems with multiple customer classes and multiple dedicated server pools under joint quality-of-service (QoS) constraints. We first analyze the case in which arrival rates are deterministic and the QoS metric is the probability a customer is queued, given by the Erlang-C formula. We use the Janssen–Van Leeuwaarden–Zwart bounds to obtain asymptotically optimal solutions to this problem. The second model considered is one in which the arrival rates are not completely known in advance (before the server staffing levels are chosen), but rather are known via a probability distribution. In this case, we provide asymptotically optimal solutions to the resulting stochastic integer program, leveraging results obtained for the case of deterministic arrivals.



Similar content being viewed by others
References
Bassamboo, A., Harrison, J.M., Zeevi, A.: Design and control of a large call center: asymptotic analysis of an LP-based method. Oper. Res. 54, 419–435 (2006)
Bassamboo, A., Randhawa, R.S., Zeevi, A.: Capacity sizing under parameter uncertainty: safety staffing principles revisited. Manag. Sci. 56, 1668–1686 (2010)
Bassamboo, A., Zeevi, A.: On a data-driven method for staffing large call centers. Oper. Res. 57(3), 714–726 (2009)
Borst, S., Mandelbaum, A., Reiman, M.I.: Dimensioning large call centers. Oper. Res. 52(1), 17–34 (2004)
Buchanan, H.E., Hildebrandt, T.H.: Note on the convergence of a sequence of functions of a certain type. Ann. Math. 9(2), 123–126 (1908)
Dentcheva, D., Prékopa, A., Ruszczyński, A.: Concavity and efficient points of discrete distributions in probabilistic programming. Math. Program. 89(1), 55–77 (2000)
Gurvich, I., Luedtke, J., Tezcan, T.: Staffing call centers with uncertain demand forecasts: A chance-constrained optimization approach. Manag. Sci. 56(7), 1093–1115 (2010)
Halfin, S., Whitt, W.: Heavy-traffic limits for queues with many exponential servers. Oper. Res. 29(3), 567–588 (1981)
Harrison, J.M., Zeevi, A.: A method for staffing large call centers based on stochastic fluid models. Manuf. Serv. Oper. Manag. 7(1), 20–36 (2005)
Jagers, A.A., Van Doorn, E.A.: On the continued Erlang loss function. Oper. Res. Lett. 5(1), 43–46 (1986)
Janssen, A.J.E.M., Van Leeuwaarden, J.S.H., Zwart, B.: Refining square root safety staffing by expanding Erlang C. Oper. Res. 59(6), 1512–1522 (2011)
Kocaga, Y.L., Armony, M., Ward, A.R.: Staffing and admission control in an M/M/N+N queue with an uncertain arrival rate. Working paper (2013)
Ralphs, T.K., Saltzman, M.J., Wiecek, M.M.: An improved algorithm for solving biobjective integer programs. Ann. Oper. Res. 147, 43–70 (2006)
Whitt, W.: Staffing a call center with uncertain arrival rate and absenteeism. Ann. Appl. Probab. 14(1), 88–102 (2006)
Acknowledgments
This research was supported by the National Science Foundation Grant CMMI-0800676. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Lemma 3
To show \(UB(\beta ,\lambda )\) is strictly decreasing in \(\lambda \), it suffices to show the denominator of (8), \(\rho +\gamma \left( \frac{\Phi (a)}{\phi (a)}+\frac{2}{3\sqrt{n}}\right) \), is strictly increasing in \(\lambda \) for any \(\beta >0\). First note that
is strictly increasing in \(\lambda \) for any \(\beta >0\), by straightforward differentiation.
Thus, we only need to prove that \(\frac{\gamma \Phi (a)}{\phi (a)}\) is non-decreasing in \(\lambda \) for any \(\beta , \lambda >0\). The derivative of \(\frac{\gamma \Phi (a)}{\phi (a)}\) with respect to \(\lambda \) is
It is easily seen that the expression above is positive if
is also positive for any \(\beta , \lambda > 0\). The denominator of (45) is strictly positive and the positivity of the numerator is again easily established by differentiation, establishing the lemma. \(\square \)
Proof of Lemma 4
With
we have that \(g(\beta ,\lambda )>0\) and is continuous in \((\beta ,\lambda )\) for all \(\beta >0, \lambda >10.\) One can verify directly that
is the only positive critical point of \(g(\beta ,\lambda )\) as a function of \(\beta \). Also, we have \(g(0,\lambda )=0\), \(\lim _{\beta \rightarrow \infty }g(\beta ,\lambda )=0\), and \(g(\widehat{\beta },\lambda )>0\), \(\forall \lambda >10\). Thus \(\widehat{\beta }\) is the global maximizer of \(g\left( \beta ,\lambda \right) \) for any \(\lambda >10\). Since \(\lim _{\lambda \rightarrow \infty }g(\widehat{\beta },\lambda )=0,\) we have \(\lim _{\lambda \rightarrow \infty }\sup _{\beta >0}g(\beta ,\lambda )=0.\) \(\square \)
Proof of Lemma 5
To show that \(\rho \phi (a)+\gamma \Phi (a)\) is strictly increasing in \(\beta \) for any sufficiently large \(\lambda \), it suffices to demonstrate that \(\rho \phi (a)+\gamma \Phi (a)\) is strictly increasing in \(n\) for any sufficiently large \(\lambda \), since \(\beta \) and \(n\) satisfy a linear relationship with a positive slope. Let \(h(n,\lambda )=\rho \phi (a)+\gamma \Phi (a)\). We have
First note that
since \(\textit{n}>\lambda \ge 1\).
Also since
the first two terms in (46) are positive. It remains then to show that the last two terms in (46) are positive, which is equivalent to \(\lambda a \le \sqrt{n}(n-\lambda )\), after some algebra. As shown by Eq. (50) in [11],
So we have \(0<a<\beta \) for sufficiently large \(\lambda \). Thus
since \(\lambda <n\). \(\square \)
Proof of Lemma 6
All the four terms in (10a) are non-negative for all \(\beta >0\), \(\lambda \ge 1\). Thus it suffices to show that \(h(\beta ,\lambda )=\rho \phi (a)+\gamma \Phi (a)\) is uniformly bounded away from 0 for all sufficiently large \(\lambda \) and \(\beta >0\), since \(\phi (\cdot )\) is positive and bounded. From Lemma 5, we know \(h(\beta ,\lambda )\) is strictly increasing in \(\beta \) for all sufficiently large \(\lambda \) and \(h(0,\lambda )=\phi (0)>0\). Thus we have that \(h(\beta ,\lambda )\) is uniformly bounded away from 0 for all sufficiently large \(\lambda \) and all \(\beta >0\). \(\square \)
Proof of Lemma 7
Let \(UB_{n}(n,\lambda )=UB(\frac{n-\lambda }{\sqrt{\lambda }},\lambda )\). Since \(n=\lambda +\beta \sqrt{\lambda }\), to show \(UB({\beta ,\lambda })\) is strictly decreasing in \(\beta \) for any \(\lambda >0\), it is enough to verify that \(UB_{n}(n,\lambda )\) is strictly decreasing in \(n\), or equivalently that
is strictly increasing in \(n\) for any \(\lambda \), where \(a\) is given in (5). This property can be established by straightforward differentiation. \(\square \)
Proof of Lemma 11
We prove that
converges uniformly to 0 in \(\beta \) as \(m \rightarrow \infty \), via induction. Let \(\underline{UB}(\beta _i,\lambda _i^m)\) denote \(1-UB(\beta _i,\lambda _i^m)\) and let \(\underline{\tilde{\alpha }}(\beta _i,\lambda _i^m)\) denote \(1-\tilde{\alpha }\left( \beta _{i},\lambda _{i}^m\right) \).
First,
where the inequality holds because both terms are positive. The latter two terms above converge to 0 by applying Theorem 8 and the fact that the Erlang-C formula and the JVLZ upper bound have range (0, 1]. Hence \(\underline{UB}(\beta _{1},\lambda _{1}^m)\underline{UB}(\beta _{2},\lambda _{2}^m)-\underline{\tilde{\alpha }}(\beta _{1},\lambda _{1}^m)\underline{\tilde{\alpha }}(\beta _{2},\lambda _{2}^m)\) converges uniformly to 0 in \(\beta =(\beta _{1},\beta _{2})\).
To apply the induction step, assume \(\forall K\in \{2,3,\ldots ,L-1\}\),
converges uniformly to 0 in \(\beta \). Some algebra yields the following:
As before, Theorem 8 implies convergence of the latter two terms, which establishes uniform convergence for the \(K+1\) case, completing the induction. \(\square \)
Proof of Lemma 15
The inequality \(\beta _{\lambda }^{G}\ge \beta _{\lambda }^{F}\) for all \(\lambda >0\) is immediate from the definitions of these quantities and the fact that \(\tilde{\alpha }(\beta ,\lambda ) \le UB(\beta ,\lambda )\) for all \(\lambda , \beta >0\).
Denote the Halfin-Whitt approximation defined in (3) in Sect. 2 as \(\alpha _{HW}(\cdot )\), and its inverse function as \(\alpha _{HW}^{-1}(\cdot )\). The function \(\alpha _{HW}(\cdot )\) is strictly decreasing and this implies that \(\alpha _{HW}^{-1}(\cdot )\) is strictly decreasing. For any \(\lambda >0\), we denote the inverse of \(UB(\cdot ,\lambda )\) as \(UB^{-1}_{\lambda }(\cdot )\). \(UB(\cdot ,\lambda )\) is strictly decreasing for any \(\lambda >0\), and this implies that \(UB^{-1}_{\lambda }(\cdot )\) is strictly decreasing for any \(\lambda >0\). By Janssen et al. [11], we have
Together with the monotonicity of \(UB(\beta ,\lambda )\) in \(\lambda \) for any \(\beta >0\), we have
Since \(\lim _{\lambda \rightarrow \infty }\epsilon _{\lambda }=\epsilon >0\), there exists \(l,u>0\), such that \(0<l \le \epsilon _{\lambda }\le u\) when \(\lambda \) is large enough. Also, since \(\alpha _{HW}^{-1}(\cdot )\) is a continuous function, by Theorem 14 we have
This gives
which implies that \(\lim _{\lambda \rightarrow \infty } \beta _{\lambda }^{G}\) exists and we denote it by \(\beta ^{*}\). Then analogous to the proof of Theorem 10 in Sect. 3, we can show that the limit of \(\beta ^{F}_{\lambda }\) exists and \(\lim _{\lambda \rightarrow \infty }\beta _{\lambda }^{G}=\lim _{\lambda \rightarrow \infty }\beta _{\lambda }^{F}=\beta ^{*}.\) \(\square \)
Rights and permissions
About this article
Cite this article
Zan, J., Hasenbein, J.J. & Morton, D.P. Asymptotically optimal staffing of service systems with joint QoS constraints. Queueing Syst 78, 359–386 (2014). https://doi.org/10.1007/s11134-014-9406-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-014-9406-x