Quantum walks on simplicial complexes

Abstract

We construct a new type of quantum walks on simplicial complexes as a natural extension of the well-known Szegedy walk on graphs. One can numerically observe that our proposing quantum walks possess linear spreading and localization as in the case of the Grover walk on lattices. Moreover, our numerical simulation suggests that localization of our quantum walks reflects not only topological but also geometric structures. On the other hand, our proposing quantum walk contains an intrinsic problem concerning exhibition of non-trivial behavior, which is not seen in typical quantum walks such as Grover walks on graphs.

Appendices

Appendix 1: Simplicial complexes

We state a quick review of homology of simplicial complexes for readers who are not familiar with it. See, e.g., [28] for details.

Definition 4.1

Let ${\mathbb {R}}^N$ be a Euclidean space and $O_N$ be the origin of ${\mathbb {R}}^N$. Let $a_0,a_1,\ldots , a_n \in {\mathbb {R}}^N$ be points so that n vectors $\{\overrightarrow{a_0a_i}\}_{i=1}^n$ are linearly independent. An n -simplex is a set $|\sigma | \subset {\mathbb {R}}^N$ given by

$$\begin{aligned} |\sigma | = \left\{ \sum _{i=1}^n \lambda _i \overrightarrow{a_0a_i}\mid \lambda _i \ge 0,\ \sum _{i=1}^n \lambda _i = 1\right\} . \end{aligned}$$

We also write $|\sigma |$ as $|a_0a_1 \ldots a_n|$ if we write the dependence of points $\{a_i\}_{i=0}^n$ explicitly. A k-face of an n-simplex $|\sigma | = |a_0a_1\ldots a_n|$ is a k-simplex $|\tau |$ generated by k points in $\{a_0\}_{i=0}^n$. In such a case, $|\sigma |$ is called a coface of $|\tau |$. An $(n-1)$-face of an n-simplex $\sigma$ is often called a primary face of $\sigma$.

For example, for a given simplex $|\sigma | = |abc|$, edges |ab|, |bc|, and |ca| are primary faces of $\sigma$. Also, vertices |a|, |b|, and |c| are 0-faces of $|\sigma |$. Finally, $|\sigma |$ is a coface of |a|, |b|, |c|, |ab|, |bc|, and |ca|.

Definition 4.2

A simplicial complex ${\mathcal {K}}$ is the collection of simplices satisfying

• If $|\sigma | \in {\mathcal {K}}$, then all faces of $|\sigma |$ are also elements in ${\mathcal {K}}$.

• If $|\sigma _1|, |\sigma _2| \in {\mathcal {K}}$ and if $|\sigma _1|\cap |\sigma _2| \not = \emptyset$, then $|\sigma _1|\cap |\sigma _2|$ is a face of both $|\sigma _1|$ and $|\sigma _2|$.

For a given simplicial complex ${\mathcal {K}}$, the union of all simplices of ${\mathcal {K}}$ is the polytope of ${\mathcal {K}}$ and is denoted by ${\mathcal {K}}$. A set P is a polyhedron if it is the polytope ${\mathcal {K}}$ of a simplicial complex ${\mathcal {K}}$.

Let ${\mathcal {K}} = \{K_k\}_{k\ge 0}$ be a simplicial complex, where $K_k = \{|\sigma | \in {\mathcal {K}} \mid |\sigma | \text { is a}~ k\text {-simplex}\}$. If $n = \max \{k \mid K_k \not = \emptyset \} < \infty$, then we call ${\mathcal {K}}$ an n -dimensional simplicial complex. For a simplicial complex ${\mathcal {K}}$ with $\dim {\mathcal {K}}= n$, its m -skeleton is defined by ${\mathcal {K}}^{(m)} := \{K_k\}_{k\ge 0}^m$ for $m\le n$. For each $|\sigma | \in K_k$, we call the number k the dimension of $|\sigma |$. Simplicial complexes admit several classes to be considered.

Definition 4.3

For a simplicial complex ${\mathcal {K}}$, a facet in ${\mathcal {K}}$ is a simplex $\sigma \in {\mathcal {K}}$ which is maximal with respect to the inclusion relation of sets. A simplicial complex ${\mathcal {K}}$ is pure if all facets in ${\mathcal {K}}$ have an identical dimension. An n-dimensional pure simplicial complex ${\mathcal {K}}$ is strongly connected if, for each $|\sigma |, |\tau | \in K_n$, there is a sequence of n-simplices $\{|\sigma _j|\}_{j=0}^k$ with $|\sigma _0| = |\sigma |$ and $|\sigma _k| = |\tau |$ such that $|\sigma _{j-1}| \cap |\sigma _j|$ is a primary face of $|\sigma _{j-1}|$ and $|\sigma _j|$ for $j=1,\ldots , n$.

Remark 4.4

We often call an $(n-1)$-face of an n-simplex $|\sigma |$ a facet of $|\sigma |$. It is completely different from facets in simplicial complexes.

The core of homology is to translate geometric objects to algebraic ones in terms of chains.

Definition 4.5

Let ${\mathcal {K}}$ be a simplicial complex. For each $|\sigma | = |a_0 a_1 \ldots a_k|\in K_k$, the associated k -chain is the function $\widehat{|\sigma |} : K_k \rightarrow \{0,1\}$ given by

$$\begin{aligned} \widehat{|\sigma |}(|\sigma '|) := {\left\{ \begin{array}{ll} 1 &{} \text { if }\sigma ' = \sigma \\ 0 &{} \text { otherwise} \end{array}\right. } \end{aligned}$$

with the following rule: for a permutation $\pi \in S_{k+1}$, identify $\widehat{|\sigma |}(\pi |\sigma |)$ with $(\det \pi )\widehat{|\sigma |}(|\sigma |)$.

Define

$$\begin{aligned} C_k({\mathcal {K}}):= \left\{ \sum _{j=1}^k a_j \widehat{|\sigma _j|}\mid a_j \in {\mathbb {Z}},\ |\sigma _j| \in K_k\right\} . \end{aligned}$$

This is called k -th chain group of ${\mathcal {K}}$, which is a ${\mathbb {Z}}$-module.

Definition 4.6

For $|\sigma | = |a_0 a_1 \ldots a_k|\in K_k$, define the boundary $\partial \widehat{|\sigma |}$ of the chain $\widehat{|\sigma |}$ by

$$\begin{aligned} \partial _k \widehat{|\sigma |} := \sum _{j=0}^k (-1)^j \widehat{|\cdots a_{j-1}a_{j+1}\cdots |}, \end{aligned}$$

which is an element in $C_{k-1}$. Extending linearly this definition, we obtain a linear map $\partial _k : C_k({\mathcal {K}})\rightarrow C_{k-1}({\mathcal {K}})$. This map is called (k -th) boundary map of ${\mathcal {K}}$.

The important property of boundary maps is the following.

Proposition 4.7

$\partial _k \circ \partial _{k+1} = 0: C_{k+1}({\mathcal {K}})\rightarrow C_{k-1}({\mathcal {K}})$.

A pair $\{C_k({\mathcal {K}}), \partial _k\}_{k\in {\mathbb {Z}}}$ consisting of sequences of chain groups and boundary maps is called a chain complex of ${\mathcal {K}}$. Then, we are ready to define homology groups.

Definition 4.8

For a simplicial complex ${\mathcal {K}}$, we define

$$\begin{aligned} Z_k({\mathcal {K}}):= \mathrm{Ker}\partial _k,\quad B_k({\mathcal {K}}):= \mathrm{Im}\partial _{k+1}. \end{aligned}$$

Both are submodules of $C_k({\mathcal {K}})$. An element in $Z_k({\mathcal {K}})$ is called a k -cycle, and an element in $B_k({\mathcal {K}})$ is called a k -boundary. Thanks to Proposition 4.7, $B_k({\mathcal {K}})$ is a submodule of $Z_k({\mathcal {K}})$. Thus, the quotient module

$$\begin{aligned} H_k({\mathcal {K}}):= Z_k({\mathcal {K}}) / B_k({\mathcal {K}}) \end{aligned}$$

can be considered. This quotient group is called the k -th homology group of ${\mathcal {K}}$. Roughly speaking, the k-th homology group describes the information of k-dimensional holes in ${\mathcal {K}}$.

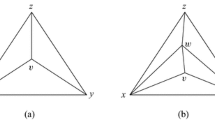
The simple example of homology is shown in Fig. 15.

Fig. 15

First homology class: a simple example. a A triangle without any 2-simplices. In this case, the chain $\widehat{|ab|} + \widehat{|bc|} + \widehat{|ca|}$ becomes a 1-cycle. Since no 2-simplices exist, this 1-cycle defines a generator of the first homology group, which indicates that this triangle has a hole. b A triangle with a 2-simplex |abc|. In this case, the chain $\widehat{|ab|} + \widehat{|bc|} + \widehat{|ca|}$ becomes a 1-cycle. On the other hand, this 1-cycle is also the boundary, which follows from $\widehat{|ab|} + \widehat{|bc|} + \widehat{|ca|} = \partial _2(\widehat{|abc|})$. This fact implies that this filled triangle has the trivial first homology group, and in other words, the filled triangle does not have any holes

Appendix 2: Concrete implementations of time evolution of S-quantum walks

In this section, we describe concrete implementations of time evolutions of S-quantum walks.

1.1 Fundamental evolution rule

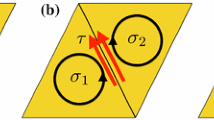
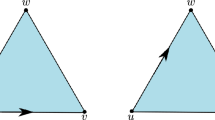
The basic implementations in our calculations are given in the case of S-quantum walks on ${\mathcal {K}}_0$. Following notations in Remark 3.1, evolution rules on lower triangles and upper triangles are defined as follows:

• Case 1: the lower triangle (Fig. 4a)

By following the definition of U, the evolution of a state on a lower triangle is given by

$$\begin{aligned}&\begin{pmatrix} \delta _{2(iN+j),0}\\ \delta _{2(iN+j),1}\\ \delta _{2(iN+j),2}\\ \delta _{2(iN+j),3}\\ \delta _{2(iN+j),4}\\ \delta _{2(iN+j),5} \end{pmatrix}\\&\quad \mapsto \begin{pmatrix} (2|w_{2(iN+j),0}|^2-1)\cdot \delta _{2(iN+j),1} \\ (2|w_{2(iN+j),1}|^2-1)\cdot \delta _{2(iN+j),2} \\ (2|w_{2(iN+j),2}|^2-1)\cdot \delta _{2(iN+j),0} \\ (2|w_{2(iN+j),3}|^2-1)\cdot \delta _{2(iN+j),4} \\ (2|w_{2(iN+j),4}|^2-1)\cdot \delta _{2(iN+j),5} \\ (2|w_{2(iN+j),5}|^2-1)\cdot \delta _{2(iN+j),3} \end{pmatrix}\\&\quad \quad + \begin{pmatrix} 2\overline{w_{2(iN+j),0}}w_{2(iN+j)+1,5} \cdot \delta _{2(iN+j)+1,3}\\ 2\overline{w_{2(iN+j),1}}w_{2((i-1)N+j)+1,4} \cdot \delta _{2((i-1)N+j)+1,5}\\ 2\overline{w_{2(iN+j),2))}}w_{2(iN+(j-1))+1,3} \cdot \delta _{2(iN+(j-1))+1,4}\\ 2\overline{w_{2(iN+j),3}}w_{2(iN+j)+1,1} \cdot \delta _{2(iN+j)+1,2}\\ 2\overline{w_{2(iN+j),4}}w_{2(iN+(j-1))+1,0} \cdot \delta _{2(iN+(j-1))+1,1}\\ 2\overline{w_{2(iN+j),5}}w_{2((i-1)N+j)+1,2} \cdot \delta _{2((i-1)N+j)+1,0} \end{pmatrix}. \end{aligned}$$

The first term of the right-hand side represents the “reflection” of waves and the second represents the “transmission” of waves to the adjacent upper triangle.

• Case 2: the upper triangle (Fig. 4b)

Similarly, the evolution of the state on an upper triangle is given by

$$\begin{aligned}&\begin{pmatrix} \delta _{2(iN+j)+1,0}\\ \delta _{2(iN+j)+1,1}\\ \delta _{2(iN+j)+1,2}\\ \delta _{2(iN+j)+1,3}\\ \delta _{2(iN+j)+1,4}\\ \delta _{2(iN+j)+1,5} \end{pmatrix}\\&\quad \mapsto \begin{pmatrix} (2|w_{2(iN+j)+1,0}|^2-1)\cdot \delta _{2(iN+j)+1,1} \\ (2|w_{2(iN+j)+1,1}|^2-1)\cdot \delta _{2(iN+j)+1,2} \\ (2|w_{2(iN+j)+1,2}|^2-1)\cdot \delta _{2(iN+j)+1,0} \\ (2|w_{2(iN+j)+1,3}|^2-1)\cdot \delta _{2(iN+j)+1,4} \\ (2|w_{2(iN+j)+1,4}|^2-1)\cdot \delta _{2(iN+j)+1,5} \\ (2|w_{2(iN+j)+1,5}|^2-1)\cdot \delta _{2(iN+j)+1,3} \end{pmatrix}\\&\quad \quad + \begin{pmatrix} 2\overline{w_{2(iN+j)+1,0}}w_{2(iN+(j+1)),4} \cdot \delta _{2(iN+(j+1)),5}\\ 2\overline{w_{2(iN+j)+1,1}}w_{2(iN+j),3} \cdot \delta _{2(iN+j),4}\\ 2\overline{w_{2(iN+j)+1,2}}w_{2((i+1)N+j),5} \cdot \delta _{2((i+1)N+j),3}\\ 2\overline{w_{2(iN+j)+1,3)}}w_{2(iN+(j+1)),2} \cdot \delta _{2(iN+(j+1)),0}\\ 2\overline{w_{2(iN+j)+1,4}}w_{2((i+1)N+j),1} \cdot \delta _{2((i+1)N+j),2}\\ 2\overline{w_{2(iN+j)+1,5}}w_{2(iN+j),0} \cdot \delta _{2(iN+j),1} \end{pmatrix}. \end{aligned}$$

As in the case of lower triangles, the first term of the right-hand side represents the “reflection” of waves and the second represents the “transmission” of waves to the adjacent lower triangle.

1.2 Evolution rule on ${\mathcal {K}}_2$: around the tetrahedron

Here, we describe the evolution rule of S-quantum walks on ${\mathcal {K}}_2$. In particular, the evolution rule near the tetrahedron is derived. Evolution rules on the region far from the tetrahedron follow from those on ${\mathcal {K}}_0$ discussed in the previous subsection. All labeling of simplices and bases on them are drawn in Figs. 16 and 17, respectively. Readers should refer to descriptions in these figures to study time evolutions stated below.

For the notation rule stated in Remark 3.1, we use bold-letter labelings shown in Fig. 16 instead of integer indices. By following the definition of U, the evolution of base elements on the 2-simplex $\mathbf{x}\in \{ \mathbf{a},\mathbf{b},\mathbf{c}, \mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D} \}$ is given in Sects. 4.2 and 4.2.2.

Fig. 16

Labeling of simplices around tetrahedron in ${\mathcal {K}}_2$. A tetrahedron is put on the infinite cylinder ${\mathcal {K}}_1$. In this figure, we put a tetrahedron, colored by green, on $\mathbf{A}\equiv |abc|$. As stated in Fig. 4a, the base element on $\mathbf{A}$ is determined by $\delta _{\mathbf{A},0} = \delta ^{(2)}_{[abc]},\ \delta _{\mathbf{A},1} = \delta ^{(2)}_{[bca]},\ \delta _{\mathbf{A},2} = \delta ^{(2)}_{[cab]},\ \delta _{\mathbf{A},3} = \delta ^{(2)}_{[acb]},\ \delta _{\mathbf{A},4} = \delta ^{(2)}_{[cba]},\ \delta _{\mathbf{A},5} = \delta ^{(2)}_{[bac]}.$ Simplices on the tetrahedron are labeled by $\mathbf{B}\equiv |abd|$, $\mathbf{C}\equiv |bcd|$, and $\mathbf{D}\equiv |cad|$. See also Fig. 17. Simplices which have effects from the tetrahedron are labeled by a, b, and c

Fig. 17

Labeling of bases on the tetrahedron. Figures here denote the graphical representations of the following bases for $l\in \{0,1,2,3,4,5\}$. Labelings of B, C, and D are followed by Fig. 16. a $\delta _{\mathbf{B}, l}$. b $\delta _{\mathbf{C}, l}$. c $\delta _{\mathbf{D}, l}$

1.2.1 2-simplices around tetrahedron

• Case 1: 2-simplex labeled a (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{a},0}\\ \delta _{\mathbf{a},1}\\ \delta _{\mathbf{a},2}\\ \delta _{\mathbf{a},3}\\ \delta _{\mathbf{a},4}\\ \delta _{\mathbf{a},5} \end{pmatrix}&\mapsto \begin{pmatrix} (2|w_{\mathbf{a},0}|^2-1)\cdot \delta _{\mathbf{a},1} \\ (2|w_{\mathbf{a},1}|^2-1)\cdot \delta _{\mathbf{a},2} \\ (2|w_{\mathbf{a},2}|^2-1)\cdot \delta _{\mathbf{a},0} \\ (2|w_{\mathbf{a},3}|^2-1)\cdot \delta _{\mathbf{a},4} \\ (2|w_{\mathbf{a},4}|^2-1)\cdot \delta _{\mathbf{a},5} \\ (2|w_{\mathbf{a},5}|^2-1)\cdot \delta _{\mathbf{a},3} \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{a},0}}w_{\mathbf{A},4} \cdot \delta _{\mathbf{A},5}\\ 2\overline{w_{\mathbf{a},1}}w_{\mathbf{a}',3} \cdot \delta _{\mathbf{a}',4}\\ 2\overline{w_{\mathbf{a},2}}w_{\mathbf{a}'',5} \cdot \delta _{\mathbf{a}'',3}\\ 2\overline{w_{\mathbf{a},3}}w_{\mathbf{A},2} \cdot \delta _{\mathbf{A},0}\\ 2\overline{w_{\mathbf{a},4}}w_{\mathbf{a}'',1} \cdot \delta _{\mathbf{a}'',2}\\ 2\overline{w_{\mathbf{a},5}}w_{\mathbf{a}',0} \cdot \delta _{\mathbf{a}',1} \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{a},0}}w_{\mathbf{B},4} \cdot \delta _{\mathbf{B},5}\\ 0\\ 0\\ 2\overline{w_{\mathbf{a},3}}w_{\mathbf{B},2} \cdot \delta _{\mathbf{B},0}\\ 0\\ 0 \end{pmatrix}. \end{aligned}$$

• Case 2: 2-simplex labeled b (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{b},0}\\ \delta _{\mathbf{b},1}\\ \delta _{\mathbf{b},2}\\ \delta _{\mathbf{b},3}\\ \delta _{\mathbf{b},4}\\ \delta _{\mathbf{b},5} \end{pmatrix} \mapsto \begin{pmatrix} (2|w_{\mathbf{b},0}|^2-1)\cdot \delta _{\mathbf{b},1} \\ (2|w_{\mathbf{b},1}|^2-1)\cdot \delta _{\mathbf{b},2} \\ (2|w_{\mathbf{b},2}|^2-1)\cdot \delta _{\mathbf{b},0} \\ (2|w_{\mathbf{b},3}|^2-1)\cdot \delta _{\mathbf{b},4} \\ (2|w_{\mathbf{b},4}|^2-1)\cdot \delta _{\mathbf{b},5} \\ (2|w_{\mathbf{b},5}|^2-1)\cdot \delta _{\mathbf{b},3} \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{b},0}}w_{\mathbf{b}'',4} \cdot \delta _{\mathbf{b}'',5}\\ 2\overline{w_{\mathbf{b},1}}w_{\mathbf{A},3} \cdot \delta _{\mathbf{A},4}\\ 2\overline{w_{\mathbf{b},2}}w_{\mathbf{b}',5} \cdot \delta _{\mathbf{b}',3}\\ 2\overline{w_{\mathbf{b},3}}w_{\mathbf{b}'',2} \cdot \delta _{\mathbf{b}'',0}\\ 2\overline{w_{\mathbf{b},4}}w_{\mathbf{b}',1} \cdot \delta _{\mathbf{b}',2}\\ 2\overline{w_{\mathbf{b},5}}w_{\mathbf{A},0} \cdot \delta _{\mathbf{A},1} \end{pmatrix} + \begin{pmatrix} 0\\ 2\overline{w_{\mathbf{b},1}}w_{\mathbf{C},4} \cdot \delta _{\mathbf{C},5}\\ 0\\ 0\\ 0\\ 2\overline{w_{\mathbf{b},5}}w_{\mathbf{C},2} \cdot \delta _{\mathbf{C},0} \end{pmatrix}. \end{aligned}$$

• Case 3: 2-simplex labeled c (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{c},0}\\ \delta _{\mathbf{c},1}\\ \delta _{\mathbf{c},2}\\ \delta _{\mathbf{c},3}\\ \delta _{\mathbf{c},4}\\ \delta _{\mathbf{c},5} \end{pmatrix}&\mapsto \begin{pmatrix} (2|w_{\mathbf{c},0}|^2-1)\cdot \delta _{\mathbf{c},1} \\ (2|w_{\mathbf{c},1}|^2-1)\cdot \delta _{\mathbf{c},2} \\ (2|w_{\mathbf{c},2}|^2-1)\cdot \delta _{\mathbf{c},0} \\ (2|w_{\mathbf{c},3}|^2-1)\cdot \delta _{\mathbf{c},4} \\ (2|w_{\mathbf{c},4}|^2-1)\cdot \delta _{\mathbf{c},5} \\ (2|w_{\mathbf{c},5}|^2-1)\cdot \delta _{\mathbf{c},3} \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{c},0}}w_{\mathbf{c}',4} \cdot \delta _{\mathbf{c}',5}\\ 2\overline{w_{\mathbf{c},1}}w_{\mathbf{c}'',3} \cdot \delta _{\mathbf{c}'',4}\\ 2\overline{w_{\mathbf{c},2}}w_{\mathbf{A},5} \cdot \delta _{\mathbf{A},3}\\ 2\overline{w_{\mathbf{c},3}}w_{\mathbf{c}',2} \cdot \delta _{\mathbf{c}',0}\\ 2\overline{w_{\mathbf{c},4}}w_{\mathbf{A},1} \cdot \delta _{\mathbf{A},2}\\ 2\overline{w_{\mathbf{c},5}}w_{\mathbf{c}'',0} \cdot \delta _{\mathbf{c}'',1} \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 2\overline{w_{\mathbf{c},2}}w_{\mathbf{D},4} \cdot \delta _{\mathbf{D},5}\\ 0\\ 2\overline{w_{\mathbf{c},4}}w_{\mathbf{D},2} \cdot \delta _{\mathbf{D},0}\\ 0 \end{pmatrix}. \end{aligned}$$

1.2.2 2-simplices on tetrahedron

• Case 1: 2-simplex labeled A (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{A},0}\\ \delta _{\mathbf{A},1}\\ \delta _{\mathbf{A},2}\\ \delta _{\mathbf{A},3}\\ \delta _{\mathbf{A},4}\\ \delta _{\mathbf{A},5} \end{pmatrix}&\mapsto \begin{pmatrix} (2|w_{\mathbf{A},0}|^2-1)\cdot \delta _{\mathbf{A},1} \\ (2|w_{\mathbf{A},1}|^2-1)\cdot \delta _{\mathbf{A},2} \\ (2|w_{\mathbf{A},2}|^2-1)\cdot \delta _{\mathbf{A},0} \\ (2|w_{\mathbf{A},3}|^2-1)\cdot \delta _{\mathbf{A},4} \\ (2|w_{\mathbf{A},4}|^2-1)\cdot \delta _{\mathbf{A},5} \\ (2|w_{\mathbf{A},5}|^2-1)\cdot \delta _{\mathbf{A},3} \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{A},0}}w_{\mathbf{b},5} \cdot \delta _{\mathbf{b},3}\\ 2\overline{w_{\mathbf{A},1}}w_{\mathbf{c},4} \cdot \delta _{\mathbf{c},5}\\ 2\overline{w_{\mathbf{A},2}}w_{\mathbf{a},3} \cdot \delta _{\mathbf{a},4}\\ 2\overline{w_{\mathbf{A},3}}w_{\mathbf{b},1} \cdot \delta _{\mathbf{b},2}\\ 2\overline{w_{\mathbf{A},4}}w_{\mathbf{a},0} \cdot \delta _{\mathbf{a},1}\\ 2\overline{w_{\mathbf{A},5}}w_{\mathbf{c},2} \cdot \delta _{\mathbf{c},0} \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{A},0}}w_{\mathbf{C},2} \cdot \delta _{\mathbf{C},0}\\ 2\overline{w_{\mathbf{A},1}}w_{\mathbf{D},2} \cdot \delta _{\mathbf{D},0}\\ 2\overline{w_{\mathbf{A},2}}w_{\mathbf{B},2} \cdot \delta _{\mathbf{B},0}\\ 2\overline{w_{\mathbf{A},3}}w_{\mathbf{C},4} \cdot \delta _{\mathbf{C},5}\\ 2\overline{w_{\mathbf{A},4}}w_{\mathbf{B},4} \cdot \delta _{\mathbf{B},5}\\ 2\overline{w_{\mathbf{A},5}}w_{\mathbf{D},4} \cdot \delta _{\mathbf{D},5} \end{pmatrix}. \end{aligned}$$

• Case 2: 2-simplex labeled B (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{B},0}\\ \delta _{\mathbf{B},1}\\ \delta _{\mathbf{B},2}\\ \delta _{\mathbf{B},3}\\ \delta _{\mathbf{B},4}\\ \delta _{\mathbf{B},5} \end{pmatrix}&\mapsto \begin{pmatrix} (2|w_{\mathbf{B},0}|^2-1)\cdot \delta _{\mathbf{B},1} \\ (2|w_{\mathbf{B},1}|^2-1)\cdot \delta _{\mathbf{B},2} \\ (2|w_{\mathbf{B},2}|^2-1)\cdot \delta _{\mathbf{B},0} \\ (2|w_{\mathbf{B},3}|^2-1)\cdot \delta _{\mathbf{B},4} \\ (2|w_{\mathbf{B},4}|^2-1)\cdot \delta _{\mathbf{B},5} \\ (2|w_{\mathbf{B},5}|^2-1)\cdot \delta _{\mathbf{B},3} \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 2\overline{w_{\mathbf{B},2}}w_{\mathbf{a},6} \cdot \delta _{\mathbf{a},4} \\ 0\\ 2\overline{w_{\mathbf{B},4}}w_{\mathbf{a},0} \cdot \delta _{\mathbf{a},1} \\ 0 \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{B},0}}w_{\mathbf{C},5} \cdot \delta _{\mathbf{C},3}\\ 2\overline{w_{\mathbf{B},1}}w_{\mathbf{D},3} \cdot \delta _{\mathbf{D},4}\\ 2\overline{w_{\mathbf{B},2}}w_{\mathbf{A},2} \cdot \delta _{\mathbf{A},0}\\ 2\overline{w_{\mathbf{B},3}}w_{\mathbf{C},1} \cdot \delta _{\mathbf{C},2}\\ 2\overline{w_{\mathbf{B},4}}w_{\mathbf{A},4} \cdot \delta _{\mathbf{A},5}\\ 2\overline{w_{\mathbf{B},5}}w_{\mathbf{D},0} \cdot \delta _{\mathbf{D},1} \end{pmatrix}. \end{aligned}$$

• Case 3: 2-simplex labeled C (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{C},0}\\ \delta _{\mathbf{C},1}\\ \delta _{\mathbf{C},2}\\ \delta _{\mathbf{C},3}\\ \delta _{\mathbf{C},4}\\ \delta _{\mathbf{C},5} \end{pmatrix}&\mapsto \begin{pmatrix} (2|w_{\mathbf{C},0}|^2-1)\cdot \delta _{\mathbf{C},1} \\ (2|w_{\mathbf{C},1}|^2-1)\cdot \delta _{\mathbf{C},2} \\ (2|w_{\mathbf{C},2}|^2-1)\cdot \delta _{\mathbf{C},0} \\ (2|w_{\mathbf{C},3}|^2-1)\cdot \delta _{\mathbf{C},4} \\ (2|w_{\mathbf{C},4}|^2-1)\cdot \delta _{\mathbf{C},5} \\ (2|w_{\mathbf{C},5}|^2-1)\cdot \delta _{\mathbf{C},3} \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 2\overline{w_{\mathbf{C},2}}w_{\mathbf{b},5} \cdot \delta _{\mathbf{b},3} \\ 0\\ 2\overline{w_{\mathbf{C},4}}w_{\mathbf{b},1} \cdot \delta _{\mathbf{b},2} \\ 0 \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{C},0}}w_{\mathbf{D},5} \cdot \delta _{\mathbf{D},3}\\ 2\overline{w_{\mathbf{C},1}}w_{\mathbf{B},3} \cdot \delta _{\mathbf{B},4}\\ 2\overline{w_{\mathbf{C},2}}w_{\mathbf{A},0} \cdot \delta _{\mathbf{A},1}\\ 2\overline{w_{\mathbf{C},3}}w_{\mathbf{D},1} \cdot \delta _{\mathbf{D},2}\\ 2\overline{w_{\mathbf{C},4}}w_{\mathbf{A},3} \cdot \delta _{\mathbf{A},4}\\ 2\overline{w_{\mathbf{C},5}}w_{\mathbf{B},0} \cdot \delta _{\mathbf{B},1} \end{pmatrix}. \end{aligned}$$

• Case 4: 2-simplex labeled D (Figs. 16 and 17)

  $$\begin{aligned} \begin{pmatrix} \delta _{\mathbf{D},0}\\ \delta _{\mathbf{D},1}\\ \delta _{\mathbf{D},2}\\ \delta _{\mathbf{D},3}\\ \delta _{\mathbf{D},4}\\ \delta _{\mathbf{D},5} \end{pmatrix}&\mapsto \begin{pmatrix} (2|w_{\mathbf{D},0}|^2-1)\cdot \delta _{\mathbf{D},1} \\ (2|w_{\mathbf{D},1}|^2-1)\cdot \delta _{\mathbf{D},2} \\ (2|w_{\mathbf{D},2}|^2-1)\cdot \delta _{\mathbf{D},0} \\ (2|w_{\mathbf{D},3}|^2-1)\cdot \delta _{\mathbf{D},4} \\ (2|w_{\mathbf{D},4}|^2-1)\cdot \delta _{\mathbf{D},5} \\ (2|w_{\mathbf{D},5}|^2-1)\cdot \delta _{\mathbf{D},3} \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 2\overline{w_{\mathbf{D},2}}w_{\mathbf{c},4} \cdot \delta _{\mathbf{c},5} \\ 0\\ 2\overline{w_{\mathbf{D},2}}w_{\mathbf{c},2} \cdot \delta _{\mathbf{c},0} \\ 0 \end{pmatrix} + \begin{pmatrix} 2\overline{w_{\mathbf{D},0}}w_{\mathbf{B},5} \cdot \delta _{\mathbf{B},3}\\ 2\overline{w_{\mathbf{D},1}}w_{\mathbf{C},3} \cdot \delta _{\mathbf{C},4}\\ 2\overline{w_{\mathbf{D},2}}w_{\mathbf{A},1} \cdot \delta _{\mathbf{A},2}\\ 2\overline{w_{\mathbf{D},3}}w_{\mathbf{B},1} \cdot \delta _{\mathbf{B},2}\\ 2\overline{w_{\mathbf{D},2}}w_{\mathbf{A},5} \cdot \delta _{\mathbf{A},3}\\ 2\overline{w_{\mathbf{D},5}}w_{\mathbf{C},0} \cdot \delta _{\mathbf{C},1} \end{pmatrix}. \end{aligned}$$