Abstract
There are at least three models of discrete-time quantum walks (QWs) on graphs currently under active development. In this work, we focus on the equivalence of two of them, known as Szegedy’s and staggered QWs. We give a formal definition of the staggered model and discuss generalized versions for searching marked vertices. Using this formal definition, we prove that any instance of Szegedy’s model is equivalent to an instance of the staggered model. On the other hand, we show that there are instances of the staggered model that cannot be cast into Szegedy’s framework. Our analysis also works when there are marked vertices. We show that Szegedy’s spatial search algorithms can be converted into search algorithms in staggered QWs. We take advantage of the similarity of those models to define the quantum hitting time in the staggered model and to describe a method to calculate the eigenvalues and eigenvectors of the evolution operator of staggered QWs.


Similar content being viewed by others
Notes
N can be infinite.
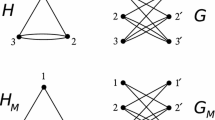
Given a line graph \(\Gamma '\), there is only one bipartite graph \(\Gamma \) such that \(L(\Gamma )=\Gamma '\) [24].
References
Aharonov, Y., Davidovich, L., Zagury, N.: Quantum random walks. Phys. Rev. A 48(2), 1687–1690 (1993)
Meyer, D.A.: From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 85(5–6), 551–574 (1996)
Farhi, E., Gutmann, S.: Quantum computation and decision trees. Phys. Rev. A 58, 915–928 (1998)
Szegedy, M.: Quantum speed-up of Markov chain based algorithms. In: Proceedings of the 45th Symposium on Foundations of Computer Science, pp. 32–41 (2004)
Ambainis, A.: Quantum walk algorithm for element distinctness. In: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science (2004)
Magniez, F., Nayak, A., Roland, J., Santha, M.: Search via quantum walk. SIAM J. Comput. 40(1), 142–164 (2011)
Krovi, H., Magniez, F., Ozols, M., Roland, J.: Finding is as easy as detecting for quantum walks. In: Proceedings of the 37th International Colloquium Conference on Automata, Languages and Programming, pp. 540–551, (2010)
Magniez, F., Santha, M., Szegedy, M.: Quantum algorithms for the triangle problem. SIAM J. Comput. 37(2), 413–424 (2007)
Mosca, M.: Quantum algorithms. In: Meyers, Robert A. (ed.) Encyclopedia of Complexity and Systems Science, pp. 7088–7118. Springer, New York (2009)
Higuchi, Yusuke, Konno, Norio, Sato, Iwao, Segawa, Etsuo: Spectral and asymptotic properties of grover walks on crystal lattices. J. Funct. Anal. 267(11), 4197–4235 (2014)
Santha, M.: Quantum walk based search algorithms. In: Proceedings of the 5th Theory and Applications of Models of Computation (TAMC08), pp. 31–46 (2008)
Patel, A., Raghunathan, K.S., Rungta, P.: Quantum random walks do not need a coin toss. Phys. Rev. A 71, 032347 (2005)
Patel, A., Raghunathan, K.S., Rahaman, MdA: Search on a hypercubic lattice using a quantum random walk. ii. \(d=2\). Phys. Rev. A 82, 032331 (2010)
Falk, M.: Quantum search on the spatial grid. arXiv:1303.4127, (2013)
Ambainis, A., Portugal, R., Nahimov, N.: Spatial search on grids with minimum memory. Quantum Inf. Comput. 15, 1233–1247 (2015)
Portugal, R., Boettcher, S., Falkner, S.: One-dimensional coinless quantum walks. Phys. Rev. A 91, 052319 (2015)
Santos, R.A.M., Portugal, R., Boettcher, S.: Moments of coinless quantum walks on lattices. Quantum Inf. Process. 14(9), 3179–3191 (2015)
Hamada, M., Konno, N., Segawa, E.: Relation between coined quantum walks and quantum cellular automata. RIMS Kokyuroku 1422, 1–11 (2005)
Strauch, F.W.: Connecting the discrete- and continuous-time quantum walks. Phys. Rev. A 74, 030301 (2006)
Aharonov, D., Ambainis, A., Kempe, J., Vazirani, U.: Quantum walks on graphs. In: Proceedings of the 33rd ACM Symposium on Theory of computing, pp. 50–59 (2000)
Shenvi, N., Kempe, J., Whaley, K.B.: Quantum random-walk search algorithm. Phys. Rev. A 67, 052307 (2003)
Grover, L.K.: Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325–328 (1997)
Portugal, Renato: Quantum Walks and Search Algorithms. Springer, New York (2013)
Whitney, H.: Congruent graphs and the connectivity of graphs. Am. J. Math. 54(1), 150–168 (1932)
Harary, F.: Graph Theory. Addison-Wesley Series in Mathematics. Perseus Books, New York (1994)
Beineke, L.W.: Characterizations of derived graphs. J. Comb. Theory 9(2), 129–135 (1970)
Krausz, J.: Démonstration nouvelle d’une théorème de Whitney sur les réseaux. Mat. Fiz. Lapok 50, 75–85 (1943)
Acknowledgments
RP acknowledges financial support from Faperj (Grant No. E-26/102.350/2013) and CNPq (Grants Nos. 304709/2011-5, 474143/2013-9, and 400216/2014-0). RAMS acknowledges financial support from Capes/Faperj E-45/2013. RP thanks helpful discussions with Stefan Boettcher and Andris Ambainis’ group. The authors thank the anonymous referees for useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Portugal, R., Santos, R.A.M., Fernandes, T.D. et al. The staggered quantum walk model. Quantum Inf Process 15, 85–101 (2016). https://doi.org/10.1007/s11128-015-1149-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11128-015-1149-z