Skip to main content
SpringerLink
Log in

Trapping and spreading properties of quantum walk in homological structure

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

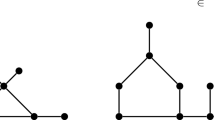
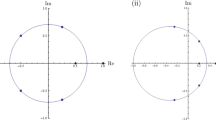
We attempt to extract a homological structure of two kinds of graphs by the Grover walk. The first one consists of a cycle and two semi-infinite lines, and the second one is assembled by a periodic embedding of the cycles in \(\mathbb {Z}\). We show that both of them have essentially the same eigenvalues induced by the existence of cycles in the infinite graphs. The eigenspace of the homological structure appears as so called localization in the Grover walks, in which the walk is partially trapped by the homological structure. On the other hand, the difference of the absolutely continuous part of spectrum between them provides different behaviors. We characterize the behaviors by the density functions in the weak convergence theorem: The first one is the delta measure at the bottom, while the second one is expressed by two kinds of continuous functions, which have different finite supports \((-1/\sqrt{10},1/\sqrt{10})\) and \((-2/7,2/7)\), respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. The one-to-one correspondence between \(V(C_4')\) and \(\mathbb {Z}\times V(\mathcal {D})\) is denoted by \(v_j\leftrightarrow (j,v)\), \((v\in \{0,0',u,d\})\) and one between \(A(C_4')\) and \(\mathbb {Z}\times A(\mathcal {D})\) is \((v_j,w_j)\leftrightarrow (j,(v,w))\) for \((v_j,w_j)\in A(C_4^{(j)})\), \((0_j,0'_{j+1})\leftrightarrow (j,(0,0'))\) and \((0_j',0_{j-1})\leftrightarrow (j,(0',0))\).

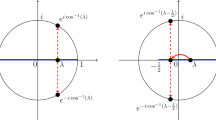
  2. More precisely, we impose the following assumptions to \(h(k)\). (i) \(h(k)=h(k+2\pi )\) for all \(k\in \mathbb {R}\), (ii) we permit discontinuity of \(h(k)\) only at \(\{2\pi n+k_j\}_{j=0}^{s-1}\), \(n\in \mathbb {N}\). (iii) for any interval, \(h(k)\) does not take a constant value.

References

  1. Ambainis, A.: Quantum walk algorithm for element distinctness. In: Proceedings of 45th IEEE Symposium Foundations of Computer Science, pp. 22–31 (2004)

  2. Ambainis, A., Kempe J., Rivosh, A.: Coins make quantum walks faster. Proceedings of 33rd ACM Symposium on Theory of Computing, pp. 37–49 (2005)

  3. Exner, P., Seba, P.: Free quantum motion on a branching graph. Rep. Math. Phys. 28, 7–26 (1989)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. Konno, N.: Quantum random walks in one dimension. Quantum Inf. Process. 1, 345–354 (2002)

    Article  MathSciNet  Google Scholar 

  5. Konno, N.: A new type of limit theorems for the one-dimensional quantum random walk. J. Math. Soc. Jpn. 57, 1179–1195 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  6. Feldman, E., Hillery, M.: Quantum walks on graphs and quantum scattering theory. Contemp. Math. 381, 71–96 (2005)

    Article  MathSciNet  Google Scholar 

  7. Gnutzmann, S., Smilansky, U.: Quantum graphs: applications to quantum chaos and universal spectral statistics. Adv. Phys. 55, 527–625 (2006)

    Article  ADS  Google Scholar 

  8. Grimmett, G., Janson, S., Scudo, P.F.: Weak limits for quantum random walks. Phys. Rev. E 69, 026119 (2004)

    Article  ADS  Google Scholar 

  9. Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Proceedings of 28th ACM Symposium on the Theory of Computing, vol. 212, pp. 212–219 (1996)

  10. Higuchi, Yu., Konno, N., Sato, I., Segawa, E.: Quantum graph walks I: mapping to quantum walks. Yokohama Math. J. 59, 34–56 (2013)

    Google Scholar 

  11. Higuchi, Yu., Konno, N., Sato I., Segawa,E.: Spectral and asymptotic properties of Grover walks on crystal lattices. arXiv:1401.0154

  12. Schanz, H., Smilansky, U.: Periodic-orbit theory of Anderson localization on graphs. Phys. Rev. Lett. 14, 1427–1430 (2000)

    Article  ADS  Google Scholar 

  13. Shenvi, N., Kempe, J., Whaley, B.: A quantum random walk search algorithm. Phys. Rev. A 67, 052307 (2003)

    Article  ADS  Google Scholar 

  14. Sunada, T.: Topological Crystallography, Surveys and Tutorials in the Applied Mathematical Sciences, vol. 6. Springer, Berlin (2013)

    Google Scholar 

  15. Szegedy, M.: Quantum speed-up of Markov chain based algorithms. In: Proceedings of 45th IEEE Symposium on Foundations of Computer Science, pp. 32–41 (2004)

  16. Tanner, G.: From quantum graphs to quantum random walks. In: Khanna, F., Matrasulov, D. (eds.) Non-linear Dynamics and Fundamental Interactions NATO Science Series II: Mathematics, Physics and Chemistry, vol 213, pp. 69–87. Springer, Netherlands (2006)

  17. Venegas-Andraca, S.E., Ball, J.L.: Processing Images in Entangled Quantum Systems. Quantum Inf. Process. 9, 1–11 (2010)

    Article  MathSciNet  Google Scholar 

  18. Venegas-Andraca S.E., Bose, S.: Storing, processing, and retrieving an image using quantum mechanics. In: Proceedings of SPIE Conference on Quantum Information and Computation, pp. 137–147 (2003)

  19. Watrous, J.: Quantum simulations of classical random walks and undirected graph connectivity. J. Comput. Syst. Sci. 62, 376–391 (2001)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

TM is grateful to the Japan Society for the Promotion of Science for the support and to the Math. Dept. UC Berkeley for hospitality. ES thanks to the financial support of the Grant-in-Aid for Young Scientists (B) of Japan Society for the Promotion of Science (Grant No. 25800088).

Author information

Authors and Affiliations

  1. Japan Society for the Promotion of Science, Hongo, Bunkyo, Tokyo, 113-8654, Japan

    Takuya Machida

  2. Department of Mathematics, University of California, Berkeley, CA, 94720, USA

    Takuya Machida

  3. Graduate School of Information Sciences, Tohoku University, Aoba, Sendai, 980-8579, Japan

    Etsuo Segawa

Authors
  1. Takuya Machida
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Etsuo Segawa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Etsuo Segawa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Machida, T., Segawa, E. Trapping and spreading properties of quantum walk in homological structure. Quantum Inf Process 14, 1539–1558 (2015). https://doi.org/10.1007/s11128-014-0819-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-014-0819-6

Keywords

Search

Navigation