Bargaining in legislatures over private and public goods with endogenous recognition

Abstract

This paper studies a sequential model of multilateral bargaining under majority rule in which legislators make decisions in both private and public good dimensions via an endogenous recognition process. Legislators can expend resources to become the proposer and to make proposals about the allocation of private and public goods. We show that legislators exert unproductive effort to be the proposer and make proposals in both dimensions depending on legislative preferences. Effort choices in equilibrium depend mainly on preferences in both distributional and ideological dimensions as well as the patience level of legislators and the legislature’s size. We also show that in a diverse legislature it may be possible to observe distributive policies when the majority of legislators have collective-leaning preferences, or vice versa.

Appendix

The main idea of for the proofs of Propositions 1 and 2 relies on the fact that there are mainly three types of decisions that can be supported in the symmetric equilibrium for different levels of $\alpha$, as in Volden and Wiseman (2007). Before starting the proofs, we state a lemma that is relatively standard in the rent-seeking literature. The result is also stated and proved by Yildirim (2007). We provide a sketch of the proof for completeness.

Lemma 1

In the one-shot legislative game in which $p_i(e) = \left\{ \begin{array}{@{}c@{\quad }l@{}} \frac{e_i}{\sum _{j\in N}e_j} & {\text {if }}e \ne \vec {0}{\text {; }}\\ \frac{1}{n} & {\text {if }}e= \vec {0}\\ \end{array}\right.$ and the recognized legislator receives an exogenous prize $\Pi _i>0$ , there exists a unique pure strategy equilibrium such that $e_i\geqslant e_j$ whenever $\frac{k_i}{\Pi _i}\le \frac{k_j}{\Pi _j}$ for some $i,j\in N$ . Moreover, if $\Pi _i=\Pi$ and $k_i=k$ for all $i\in N$ , then $e_i=e_j>0$ and thus $p_i(e)=p_{j}(e)=\frac{1}{n}$ for all $i,j\in N$ .

Proof

First, notice that $e_i=0$ for all $i\in N$ cannot be an equilibrium. The expected equilibrium payoff for legislator i satisfies the following program: $v_i=\max _{e_i}\{p_i(e)\Pi _i-k_ie_i\}.$ Taking the derivative of the terms inside the brackets yields $\frac{\partial p_i(e)}{\partial e_i}\Pi _i-k_i\leqslant 0 ( = 0 \text { if } e_i > 0).$⁶ This implies $\frac{\sum _{j\ne i}e_j}{(\sum _je_j)^2}=\frac{1-p_i}{\sum _je_j}=\frac{k_i}{\Pi _i}$, which is equivalent to $\sum _je_j=\frac{(n-1)}{\sum {\frac{k_i}{\Pi _i}}}$. Therefore, $p_i=1-(n-1)\frac{\frac{k_i}{\Pi _i}}{\sum _j{\frac{k_j}{\Pi _j}}}$. Note that if $\Pi _i=\Pi$ and $k_i=k$ for all $i\in N$, then $p_i=\frac{1}{n}$. For a proof of uniqueness for the general case, see Szidarovszky and Okuguchi (1997). $\square$

Proof

(Proposition 1) If legislator i is recognized in session t, he chooses a proposal according to the following program: $d^i\in argmax_{d}~\alpha x_i^i+(1-\alpha )y^i$ subject to $\alpha x_j^i+(1-\alpha )y^i=\delta v_j$ for all $j\in C$ where $\mid C \mid =\dfrac{n+1}{2}$ and $y^i+\sum _{k\in N}x_k^i\le 1.$ Notice that $\alpha x_i^i+(1-\alpha )y^i=(2\alpha -1)x_i^i+(1-\alpha )+(\alpha -1)\sum _{k\in C\setminus \{i\}}x_k^i.$ This implies that $d^i=(1,0,\dots ,0)$ if $\alpha \in [0,\dfrac{1}{2}].$ Therefore, being recognized does not affect the expected payoffs since the approved proposal involves only the public good dimension. Then, legislator i’s continuation payoff is $v_i=max_{e_i}p_i(e)(1-\alpha )+(1-p_i(e))(1-\alpha )-ke_i$. This implies $e_i=0$$\forall$$i\in N.$ Hence, legislators do not exert effort because it is costly and recognition probabilities are identical. Therefore, the legislator who is recognized in the first session will put all resources towards the public good dimension and this decision will be approved by all legislators. $\square$

Proof

(Proposition 2) Suppose legislator i is recognized in the first session, and he keeps $x_i^i$ for himself and invests $y^i=1-x_i^i$ in the public good dimension. Suppose this decision is rejected by a majority in the legislature. Let j be a member of the coalition who voted no in the first session. He then expects that a decision can be approved in the second session if and only if $x_j^j=x_i^i-\epsilon _j$ and $y^j=y^i+\epsilon _j$, where $\epsilon _j\in (0,1)$ in the mixed part of the equilibrium. By stationarity, legislator $j\ne i$ would make the same decision if he is recognized in the first session and the decision is accepted. This implies that legislator i’s decision is not optimal and cannot be a part of the equilibrium since he is better off making the same proposal as legislator j in the first session. Therefore, the game ends in the first session and $x_i^i=x_j^j=x$ for all $i,j\in N$. The legislative game can then be thought as a one-shot game with a fixed prize $(\Pi =\alpha x)$.⁷ From Lemma 1, $p_i=\frac{1}{n}$ and $e_i=e_j=e=\dfrac{(n-1)}{n^2k}\Pi >0$ for all $i,j\in N$. In the voting stage, non-proposer j votes yes if and only if $(1-\alpha )(1-x)\geqslant \delta p_j(e)\alpha x+\delta (1-\alpha )(1-x)-\delta ke_j$. That is, $(1-\alpha )(1-x)\geqslant \delta p_j(e)\alpha x+\delta (1-\alpha )(1-x)-\delta \dfrac{(n-1)}{n^2}\alpha x.$ This implies that $x\le \dfrac{(1-\alpha )(1-\delta )n^2}{\delta \alpha +(1-\alpha )(1-\delta )n^2}.$ Then, to maximize his utility, legislator i sets $x=\dfrac{(1-\alpha )(1-\delta )n^2}{\delta \alpha +(1-\alpha )(1-\delta )n^2}$ and $y=\dfrac{\delta \alpha }{\delta \alpha +(1-\alpha )(1-\delta )n^2}$. Given these equilibrium decisions for the mixed part of the equilibrium, the equilibrium level of effort exerted by a legislator can be written as $e=\dfrac{(n-1)}{n^2k}\Pi =\dfrac{(n-1)}{n^2k}\alpha x=\dfrac{(n-1)}{k}\left( \dfrac{\alpha (1-\alpha )(1-\delta )}{\delta \alpha +(1-\alpha )(1-\delta )n^2}\right) >0.$ Note that this decision is approved unanimously in the first session. Legislator i’s utility is then given by $U_{I}=\Pi +(1-\alpha )y-ke=\Pi (2-\dfrac{1}{\alpha }-\dfrac{n-1}{n^2})+1-\alpha .$

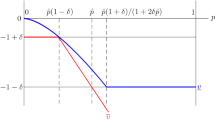
In the particularistic dimension of the equilibrium, i.e. $\alpha \in (\alpha _{p},1]$, suppose legislator i keeps $x_i^i=x'=1-\theta (\frac{n-1}{2})$ for himself, invests $y^i=0$ in the public good, and divides the remaining surplus $1-x'$ between $\frac{n-1}{2}$ legislators at random. By stationarity, the legislative game can be thought as a one-shot game with a prize $(\Pi =\alpha x')$. From Lemma 1, $e_i=e_j=\dfrac{(n-1)}{n^2k}\Pi ^{'}>0$ and thus $p_i=p_j=\frac{1}{n}$ for all $i,j\in N$. By symmetry, $x_i^i=x_j^j=x'=1-\left( \frac{n-1}{2}\right) \theta$ for all $i,j\in N$. This implies that the model reduces to that of Baron and Ferejohn (1989). We state the rest of the proof for completeness. In the voting stage, non-proposer j votes yes if and only if $\alpha \theta \geqslant \delta p_j(e)\alpha (1-\frac{n-1}{2}\theta )+\delta (1-p_j(e))\frac{1}{2}\alpha \theta -\delta ke_{j}.$ This implies $\theta \geqslant \dfrac{2\delta }{2n^2-\delta (n-1)^2}$. Then, to maximize utility, legislator i sets $\theta =\dfrac{2\delta }{2n^2-\delta (n-1)^2}$. Note that this decision is approved by a majority in the first session and the optimal effort level directly becomes (from Lemma 1) $e=\dfrac{\alpha (n-1)}{n^2k}\left( 1-\dfrac{(n-1)\delta }{2n^2-\delta (n-1)^2}\right) >0$. Legislator i’s utility is then given by $U_{II}=\Pi '-ke'=\Pi '(1-\dfrac{n-1}{n^2}).$ We now show how to find the cut-off value $\alpha _p$ by comparing the stage utility levels of the proposer. If $\alpha \in [\alpha _{p},1]$, then we should have $U_{II}\geqslant U_{I}$. Then $\alpha _p$ is given by solving the following equation: $U_{II}=\Pi '-ke'=\Pi '(1-\frac{n-1}{n^2})\ge U_{I}=\Pi (2-\dfrac{1}{\alpha }-\dfrac{n-1}{n^2})+1-\alpha$. This implies that the cutoff point is $\alpha _p=\dfrac{n[1-2n-\delta n^2+(\delta -1)n^3]}{\delta (n^4-2n^2+2n-1)-n(n^3+2n^2+1)}$. $\square$

Proof

(Proposition 3) Note that $y=\dfrac{\delta \alpha }{\delta \alpha +(1-\alpha )(1-\delta )n^2}$ in the mixed part of the equilibrium. It is then easy to see that $\dfrac{\partial y}{\partial \delta }>0$, $\dfrac{\partial y}{\partial n}<0$, and $\dfrac{\partial y}{\partial \alpha }>0$. $\square$

Proof

(Proposition 4) Note that $e=\dfrac{(n-1)}{k}\left( \dfrac{\alpha (1-\alpha )(1-\delta )}{\delta \alpha +(1-\alpha )(1-\delta )n^2}\right)$ in the mixed part of the equilibrium. It is easy to see that $\dfrac{\partial e}{\partial \delta }<0$ and $\dfrac{\partial e}{\partial k}<0$. Moreover,

$$\begin{aligned} \dfrac{\partial e}{\partial n}=\dfrac{\alpha (1-\alpha )(1-\delta )}{k(\delta \alpha +(1-\alpha )(1-\delta )n^2 )^2}[\delta \alpha -(1-\alpha )(1-\delta )(n^2-2n)]. \end{aligned}$$

This implies that $\dfrac{\partial e}{\partial n}<0$ if $n> \sqrt{\dfrac{\delta \alpha +(1-\delta )(1-\alpha )}{(1-\delta )(1-\alpha )}}+1$. Finally,

$$\begin{aligned} \dfrac{\partial e}{\partial \alpha }=\dfrac{(n-1)(1-\delta )}{k\left\{ \delta \alpha +(1-\alpha )(1-\delta )n^2\right\} ^2}\left\{ -\delta \alpha ^2+(1-\alpha )^2(1-\delta )n^2\right\} . \end{aligned}$$

If $n>\sqrt{\left( \dfrac{\delta }{1-\delta }\right) }\left( \dfrac{\alpha }{1-\alpha }\right)$, then $\dfrac{\partial e}{\partial \alpha }>0$. Therefore, the sufficient condition for both comparative statics results for the optimal effort level to hold is

$$\begin{aligned} n>\max \left\{ \sqrt{\dfrac{\delta \alpha +(1-\delta )(1-\alpha )}{(1-\delta )(1-\alpha )}}+1, \sqrt{\left( \dfrac{\delta }{1-\delta }\right) }\left( \dfrac{\alpha }{1-\alpha }\right) \right\} . \end{aligned}$$

$\square$

Proof

(Proposition 5) Note that $e'=\dfrac{\alpha (n-1)}{n^2k}\left( 1-\dfrac{(n-1)\delta }{2n^2-\delta (n-1)^2}\right)$ in the particularistic part of the equilibrium. It is then easy to see that $\dfrac{\partial e^{'}}{\partial n}<0$, $\dfrac{\partial e^{'}}{\partial \delta }<0$, $\dfrac{\partial e^{'}}{\partial k}<0$, and $\dfrac{\partial e^{'}}{\partial \alpha }>0$. $\square$

Proof

(Proposition 6) We show that legislators have incentives to exert positive effort when the other type of legislators exert zero effort.

Case 1 The majority consists of legislators who support public good provision, i.e. $m>\dfrac{n-1}{2}$. First, suppose that both types of legislators exert zero effort, i.e. $(e_i,e_j)=(0,0)~\forall ~i\in A {\text { and }} \forall ~j\in B$. For any legislator $j\in B$, he takes x for himself and gives $1-x$ for the supporters of public good provision. In the critical voting stage, non-proposer legislator $i \in A$ will support the decision of any legislator $j\in B$ if and only if $(1-x)\ge \delta \left( \dfrac{m}{n}+\dfrac{(n-m)}{n}(1-x)\right) .$ This implies $x=\dfrac{n-\delta n}{n-\delta n+\delta m}$ and $y=\dfrac{\delta m}{n-\delta n+ \delta m}$. Then the expected utility for the legislators $j\in B$ is $EU_j=\dfrac{(n-m)}{n}\left( \alpha _p\dfrac{1}{n-m}x\right) +\dfrac{m}{n}\alpha _p0=\dfrac{1-\delta }{n-\delta n+\delta m}$. Similarly, the expected utility for the legislators $i\in A$ is $EU_i=\dfrac{m}{n}+\dfrac{\delta (n-m)m}{n(n-\delta n+\delta m)}.$ Now we ask whether there exists an incentive for any legislator to exert positive effort when both types exert zero effort initially. If $e_i=0 \forall ~i\in A$, then any legislator $j\in B$ exerts $e_j >0$ and a distributive legislator, $j\in B$, will be recognized with certainty. Then, to exert positive effort, we must have the following: $\dfrac{n-\delta n}{(n-m)(n-\delta n +\delta m)}-ke_j\ge \dfrac{1-\delta }{n-\delta n +\delta m}$. Then, $e_j\in \left( 0,\dfrac{(1-\delta )m}{(n-m)(n-\delta n+ \delta m)k}\right]$. It is clear that in this interval, we find that exerting positive effort makes legislator $j \in B$ better off while $e_i=0 \forall ~ i\in A$. If $e_j=0 \forall ~j\in B$, any legislator $i\in A$ exerts $e_i >0$ and any collective legislator, $i\in A$, will be recognized with certainty. Note that there exists only the ideological dimension in the equilibrium since the majority consists of legislators who support public good provision. Then, to exert positive effort, we must have the following: $1-ke_i\ge \dfrac{m}{n} +\dfrac{\delta (n-m)m}{n(n- \delta n +\delta m)}$. Then, $e_i\in \left( 0,\dfrac{(n-m)(1-\delta )}{(n-\delta n +\delta m)k}\right]$. Obviously, in this interval, we find that exerting positive effort makes legislator $i \in A$ better off while $e_j=0 \forall ~j\in B$. Thus, exerting positive effort makes each type of legislator better off if the other group exerts zero effort. Therefore, we must have $(e_i,e_j)\ne (0,0)$$\forall ~i\in A$ and $\forall ~j\in B$. Then, for any $i\in A$,

$$\begin{aligned} EU_i=\dfrac{me_i}{me_i+(n-m)e_j}+\dfrac{(n-m)e_j}{me_i+(n-m)e_j}\left( \dfrac{\delta e_i[m(1-ke_i)-ke_j(n-m)]}{me_i+(1-\delta )(n-m)e_j}\right) -ke_i, \end{aligned}$$

and for any $j\in B$,⁸

$$\begin{aligned} EU_j=\dfrac{e_j}{me_i+(n-m)e_j}\left( \dfrac{(1-\delta +\delta ke_i)(me_i+(n-m)e_j)}{me_i+(1-\delta )(n-m)e_j}\right) -ke_j. \end{aligned}$$

Given the expected payoffs, it is clear that $\exists$$(e_i,e_j)\ne (0,0)$ such that $EU_i(e_i,e_j=\epsilon )>EU_i(0,e_j=\epsilon )$ and $EU_j(e_i=\epsilon ^{'},e_j)>EU_j(e_i=\epsilon ^{'},0)$, where $\epsilon$ and $\epsilon ^{'}$ are very small positive real numbers.

Case 2 The majority consists of legislators who support private good provision, i.e. $m<\dfrac{n-1}{2}$. First, suppose that both types of legislators exert zero effort, i.e. $(e_i,e_j)=(0,0) \forall ~i\in A {\text { and }} \forall ~j\in B$. Any recognized legislator $j\in B$ gives $x^{''}$ particularistic goods to $\dfrac{n-1}{2}$ other legislators who support private good allocation and keeps $x^P=1-\left( \dfrac{n-1}{2}\right) x^{''}$. Any recognized legislator $i\in A$ gives $x^{'}$ particularistic goods to $\dfrac{n+1-2m}{2(n-m)}$ distributive legislators and puts $y=1-\left( \dfrac{n+1-2m}{2(n-m)}\right) x^{'}$ towards the collective. In the critical voting stage, if a collective one is recognized, the non-proposer distributive legislator votes “Yes” if and only if

$$\begin{aligned} \alpha _px^{'}+(1-\alpha _p)y \ge \delta \left\{ \dfrac{1}{n}x^P+\left( \dfrac{n-m-1}{n}\right) \dfrac{(n-1)}{2(n-m-1)}\alpha _px^{''}+\dfrac{m}{n}\left[ \dfrac{(n+1-2m)}{2(n-m)}\alpha _{p}x^{'}+(1-\alpha _{p})y\right] \right\} . \end{aligned}$$

Furthermore, in the critical voting stage, if a distributive one is recognized, the non-proposer distributive legislator votes “Yes” if and only if

$$\begin{aligned} \alpha _{p}x^{''}\ge \delta \left\{ \dfrac{1}{n}x^P+\left( \dfrac{n-m-1}{n}\right) \dfrac{(n-1)}{2(n-m-1)}\alpha _px^{''}+\dfrac{m}{n}\left[ \dfrac{(n+1-2m)}{2(n-m)}\alpha _{p}x^{'}+(1-\alpha _{p})y\right] \right\} . \end{aligned}$$

Also note that $\alpha _p=1$ and in equilibrium we must have $\alpha _px^{'}+(1-\alpha _p)y=\alpha _px^{''}$, and since $\alpha _p=1$, we have $x^{'}=x^{''}$. Optimality then requires that

$$\begin{aligned} x^{'}= & \dfrac{2\delta (n-m)}{2(n-m)n-\delta m(n+1-2m)}=x^{''}, \\ x^P= & \dfrac{2(n-m)n-\delta m(n+1-2m)-\delta (n-m)(n-1)}{2(n-m)n-\delta m(n+1-2m)}, \end{aligned}$$

and $y=\dfrac{2(n-m)n-\delta (m+1)(n+1-2m)}{2(n-m)n-\delta m(n+1-2m)}$. Then the expected utility for legislators $i\in A$ is

$$\begin{aligned} EU_i^{0}=\dfrac{m}{n}(1-\alpha _{c})y+\dfrac{(n-m)}{n}\alpha _{c}0 = \dfrac{2mn(n-m)-\delta m(m+1)(n+1-2m)}{2(n-m)n^2-\delta mn(n+1-2m)}. \end{aligned}$$

Similarly, the expected utility for legislators $j\in B$ is

$$\begin{aligned} EU_j^{0}=\dfrac{m(n+1-2m)}{2n(n-m)}\alpha _{p}x^{'}+\dfrac{1}{n}\alpha _{p}x^P+\dfrac{(n-m-1)}{n}\dfrac{(n-1)}{2(n-m-1)}\alpha _{p}x^{''}=\dfrac{2(n-m)}{2(n-m)n-\delta m(n+1-2m)}. \end{aligned}$$

Now we check whether there exists any incentive for any legislator to exert positive effort when the other type exerts zero effort initially. If $e_i=0 \forall ~i\in A$, any legislator $j\in B$ exerts $e_j >0$ and a distributive legislator, $j\in B$, will be recognized directly. Then, to exert positive effort, the following equation must hold:

$$\begin{aligned} \dfrac{x^P}{(n-m)}+\dfrac{(n-m-1)}{(n-m)}\left( \dfrac{(n-1)}{2(n-m-1)}x^{'}\right) -ke_j\ge EU_j^{0} =\dfrac{2(n-m)}{2(n-m)n-\delta m(n+1-2m).} \end{aligned}$$

Then, when $e_j\in \left( 0,\dfrac{2(n-m)m-\delta m(n+1-2m)}{kB(n-m)}\right]$ where $B=2(n-m)n-\delta m(n+1-2m)$, the distributive legislator exerts positive effort while the collective ones are inactive. If $e_j=0 \forall ~j\in B$, then any legislator $i\in A$ exerts $e_i>0$ and collective ones are recognized directly. Then, to exert positive effort, the following equation must hold:

$$\begin{aligned} \dfrac{2(n-m)n-\delta (m+1)(n+1-2m)}{2(n-m)n-\delta m(n+1-2m)}-ke_i\ge \dfrac{m}{n}(1-\alpha _{c})y=EU_i^{0}= \dfrac{2mn(n-m)-\delta m(m+1)(n+1-2m)}{2(n-m)n^2-\delta mn(n+1-2m)}. \end{aligned}$$

When $e_i\in \left( 0, \dfrac{C}{kD}\right]$ where $C=2(n-m)^2n-\delta (m+1)^2(n+1-2m)$ and $D=2(n-m)n^2-\delta mn(n+1-2m)$, then the collective legislator will exert positive effort while the distributive ones are inactive. As a result, each type of legislator becomes better off by exerting positive effort if the other type of legislator exerts zero effort. Thus, we must have $(e_i,e_j)\ne (0,0) \forall ~i\in A$ and $\forall ~j\in B$. Then, for any $i\in A$,

$$\begin{aligned} EU^{'}_i=\left( \dfrac{me_i}{me_i+(n-m)e_j}\right) (1-\alpha _{c})\left\{ 1-\left( \dfrac{n+1-2m}{2}\right) \eta \right\} -ke_i, \end{aligned}$$

and for any $j\in B$,⁹

$$\begin{aligned} EU^{'}_j=\left( \dfrac{me_i}{me_i+(n-m)e_j}\right) \alpha _{p}\eta +\left( \dfrac{e_j}{me_i+(n-m)e_j}\right) \alpha _{p}\eta ^{P}+\dfrac{(n-1)e_j}{2(me_i+(n-m)e_j)}\alpha _{p}\nu -ke_j. \end{aligned}$$

Given the expected payoffs, it is clear to see that $\exists$$(e_i,e_j)\ne (0,0)$ such that $EU^{'}_i(e_i,e_j=\epsilon )>EU^{'}_i(0,e_j=\epsilon )$ and $EU^{'}_j(e_i=\epsilon ^{'},e_j)>EU^{'}_j(e_i=\epsilon ^{'},0)$, where $\epsilon$ and $\epsilon ^{'}$ are very small positive real numbers. $\square$

Proof

(Proposition 7) A collective legislator is recognized with the probability $\dfrac{me_i}{me_i+(n-m)e_j}$. If a collective one is recognized, decision d is accepted by the majority and the game ends in the first session with stage utilities $U_i=1-ke_i$ and $U_j=-ke_j$. A distributive legislator is recognized with the probability $\dfrac{(n-m)e_j}{me_i+(n-m)e_j}$. In the critical voting stage, a non-proposer collective legislator will say “Yes” if and only if

$$\begin{aligned} (1-\alpha _c)(1-x)\ge \delta \left( \dfrac{me_i}{me_i+(n-m)e_j}(1-\alpha _c)+\dfrac{(n-m)e_j}{me_i+(n-m)e_j}(1-\alpha _c)(1-x)-ke_i \right) . \end{aligned}$$

Note that $\alpha _c=0$. Therefore, we have $x=\frac{(1-\delta +\delta ke_i)(me_i+(n-m)e_j)}{me_i+(1-\delta )(n-m)e_j}$ and $y=\frac{\delta e_i[m(1-ke_i)-ke_j(n-m)]}{me_i+(1-\delta )(n-m)e_j}$. Moreover, the game ends in the first session since the distributive legislator gives the amount that satisfies the continuation value of collective legislators, which makes them indifferent between saying yes or no. Now we show that the optimal effort levels $e_i^{*}$ and $e_j^{*}$ exist. Indeed, the intersection point(s) of best response correspondences for each group of legislators is not an empty set. The expected utility for the distributive legislator, denoted by $EU_i$, is

$$\begin{aligned} EU_i=\dfrac{me_i}{me_i+(n-m)e_j}+\dfrac{(n-m)e_j}{me_i+(n-m)e_j}\left( \dfrac{\delta e_i[m(1-ke_i)-ke_j(n-m)]}{me_i+(1-\delta )(n-m)e_j}\right) -ke_i. \end{aligned}$$

Similarly, the expected utility for the distributive, denoted by $EU_j$, is

$$\begin{aligned} EU_j=\dfrac{e_j}{me_i+(n-m)e_j}\left( \dfrac{(1-\delta +\delta ke_i)(me_i+(n-m)e_j)}{me_i+(1-\delta )(n-m)e_j}\right) -ke_j. \end{aligned}$$

Note that by Proposition 6, we have $(e_i,e_j)\not =(0,0)$, and thus we do not have any possible continuity problems. Moreover, $e_i$ and $e_j$ are bounded above because of the direct cost-benefit analysis. Then, by Debreu (1952), Fan (1952), and Glicksberg (1952),¹⁰ there exists $(e_i^*,e_j^*)$ such that the intersection of two best response correspondences are not an empty set. $\square$

Proof

(Proposition 8) Collective and distributive legislators are recognized with the probabilities $\dfrac{me_i}{me_i+(n-m)e_j}$ and $\dfrac{(n-m)e_j}{me_i+(n-m)e_j}$, respectively. If a collective one is recognized, he gives $\eta$ private good to $\left( \dfrac{n+1-2m}{2}\right)$ distributive legislators selected at random and puts $y=1-\left( \dfrac{n+1-2m}{2}\right) \eta$ towards the public good. If a distributive legislator is recognized, then he gives $\nu$ private good to $\left( \dfrac{n-1}{2}\right)$ other distributive legislators and keeps $\eta ^P=1-\left( \dfrac{n-1}{2}\right) \nu$ for himself. Therefore, the expected utilities for each type of legislator become

$$\begin{aligned} EU^{'}_i=\dfrac{me_i}{me_i+(n-m)e_j}(1-\alpha _{c})\left[ 1-\left( \dfrac{n+1-2m}{2}\right) \eta \right] +\dfrac{(n-m)e_j}{me_i+(n-m)e_j}(1-\alpha _{c})0-ke_i \end{aligned}$$

and

$$\begin{aligned} EU^{'}_j=\dfrac{me_i}{me_i+(n-m)e_j}\alpha _{p}\eta +\dfrac{e_j}{me_i+(n-m)e_j}\alpha _{p}\eta ^{P} +\left( \dfrac{(n-m-1)e_j}{me_i+(n-m)e_j}\right) \left( \dfrac{n-1}{2(n-m-1)}\right) \alpha _{p}\nu -ke_j. \end{aligned}$$

In the critical voting stage, a non-proposer distributive legislator votes yes if and only if

Case 1 If the collective legislator is recognized,

$$\begin{aligned} \alpha _p \eta +(1-\alpha _p)y\ge & \, \delta \left[ \dfrac{e_j}{me_i+(n-m)e_j}\alpha _p\eta ^P+\left( \dfrac{(n-m-1)e_j}{me_i+(n-m)e_j}\right) \dfrac{(n-1)}{2(n-m-1)}\alpha _p\nu \right] \\&+\,\delta \left[ \left( \dfrac{me_i}{me_i+(n-m)e_j}\right) \dfrac{(n+1-2m)}{2(n-m)}\alpha _p\eta -ke_j\right] . \end{aligned}$$

Case 2 If the distributive legislator is recognized,

$$\begin{aligned} \alpha _p \nu\ge &\, \delta \left[ \left( \dfrac{e_j}{me_i+(n-m)e_j}\right) \alpha _p\eta ^P+\left( \dfrac{(n-m-1)e_j}{me_i+(n-m)e_j}\right) \dfrac{(n-1)}{2(n-m-1)}\alpha _p\nu \right] \\&+\,\delta \left[ \left( \dfrac{me_i}{me_i+(n-m)e_j}\right) \left( \dfrac{n+1-2m}{2(n-m)}\right) \alpha _p\eta -ke_j\right] . \end{aligned}$$

Then, in the equilibrium, we must have $\alpha _p\eta +(1-\alpha _p)y=\alpha _p\nu .$ Since $\alpha _p=1$, we have $\eta =\nu =\dfrac{2(n-m)\delta e_j(1-k(me_i+(n-m)e_j))}{2(n-m)(me_i+(n-m)e_j)-\delta (n+1-2m)me_i}$ with $\eta ^P=1-\left( \dfrac{n-1}{2}\right) \eta$ and $y=1-\left( \dfrac{n+1-2m}{2}\right) \eta$. Note that the game ends in the first session since both collective and distributive legislators offer the continuation value of other distributive legislators. This makes them indifferent to saying yes or no. By Proposition 6, we have $(e_i,e_j)\ne (0,0)$. Therefore, we do not have a possible continuity problem. Moreover, $e_i$ and $e_j$ are bounded above because of the direct cost-benefit analysis. Then, by Debreu (1952), Fan (1952), and Glicksberg (1952), there is a pair $(e_i^*,e_j^*)$ such that the intersection of best response correspondences are not an empty set. $\square$