Abstract
We consider the benchmark stochastic frontier model where inefficiency is directly influenced by observable determinants. In this setting, we estimate the stochastic frontier and the conditional mean of inefficiency without imposing any distributional assumptions. To do so we cast this model in the partly linear regression framework for the conditional mean. We provide a test of correct parametric specification of the scaling function. An empirical example is also provided to illustrate the practical value of the methods described here.







Similar content being viewed by others
Notes
We note that our approach to estimating the stochastic frontier model is different than alternative approaches which also exist in the nonparametric realm. For example, Kumbhakar et al. (2007) and Martins-Filho and Yao (2015) nonparametrically estimate the stochastic production frontier but require distributional assumptions, Simar et al. (2014) estimate the same model in a nonparametric fashion, but only require the scaling property for the distribution of inefficiency. Lastly, Kneip et al. (2015) estimate a stochastic production frontier but require that the distribution of noise is log normally distributed [their model is an extension of the work of Hall and Simar (2002)].
See Sect. 4 in Simar et al. (2014).
We are indebted to Peter Schmidt for drawing this issue to our attention and the discussion that follows.
We are grateful to an anonymous reviewer for making this point to us.
See Appendix 4 for a more detailed discussion of imposing nonnegativity on the estimator for g(Z i ).
See Appendix 3 for a more detailed discussion of kernel estimation of both T(X i ) and g(Z i ).
All of the correlations are equal to ρ in this setting.
We note that our estimates of \(\hat u({Z_{it}})\) were always greater than 0 even though it is possible to have negative estimates given that if β 0 were negative, this could become confounded in our estimation.
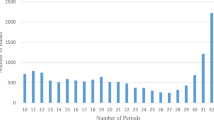
Almost 10 % of our 3503 observations produced estimated cash flow gradients which were positive and statistically significant. Compare this to only nine total observations having estimated positive gradients for firm assets.
References
Aigner DJ, Lovell CAK, Schmidt P (1977) Formulation and estimation of stochastic frontier production functions. J Econ 6(1):21–37
Alvarez A, Amsler C, Orea L, Schmidt P (2006) Interpreting and testing the scaling property in models where inefficiency depends on firm characteristics. J Prod Anal 25:201–212
Amsler C, Schmidt P, Tsay W-J (2015) A post-truncation parameterization of truncated normal technical inefficiency. J Prod Anal 44(2):209–220
Battese GE, Coelli TJ (1995) A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empir Econ 20(1):325–332
Buja A, Hastie T, Tibshirani R (1989) Linear smoothers and additive models (with discussion). Ann Stat 17(3):453–455
Caudill SB, Ford JM (1993) Biases in frontier estimation due to heteroskedasticity. Econ Lett 41(1):17–20
Caudill SB, Ford JM, Gropper DM (1995) Frontier estimation and firm-specific inefficiency measures in the presence of heteroskedasticity. J Bus Econ Stat 13(1):105–111
Cleary S (1999) The relationship between firm investment and financial status. J Financ LIV:673–692
Daraio C, Simar L, Wilson PW (2015), Testing the “separability” condition in two-stage nonparametric models of production. Institute of Economics, Scuola Superiore Sant'Anna, LEM Working Paper Series, 2015/21
Deprins D (1989) Estimation de frontieres de Production et Mesures de l'Efficacite Technique. CIACO, Louvain-la-Neuve, Belgium
Deprins P, Simar L (1989a) Estimating technical efficiencies with corrections for environmental conditions with an application to railway companies. Ann Public Coop Econ 60(1):81–102
Deprins P, Simar L (1989b) Estimation de frontieres deterministes avec factuers exogenes d’inefficacite. Annales d’Economie et de Statistique 14:117–150
Du P, Parmeter CF, Racine JS (2013) Nonparametric kernel regression with multiple predictors and multiple shape constraints. Stat Sin 23(3):1347–1371
Fan Y, Li Q, Stengos T (1992) Root-n consistent semiparametric regression with conditionally heteroscedastic disturbances. Working Paper 1992-17, University of Guelph, Department of Economics
Fan Y, Li Q, Stengos T (1995) Root-N-consistent semiparametric regression with conditionally heteroskedastic disturbances. J Quant Econ 11(2):229–240
Fan Y, Li Q, Weersink A (1996) Semiparametric estimation of stochastic production frontier models. J Bus Econ Stat 14(4):460–468
Fazzari SM, Hubbard RG, Petersen BC (1988) Financing constraints and corporate investment. Brook Pap Econ Act 1:141–195
Gao Q, Liu L, Racine JS (2015) A partially linear kernel estimator for categorical data. Econom Rev 34(6-10):958–977
Hall P, Simar L (2002) Estimating a changepoint, boundary or frontier in the presence of observation error. J Am Stat Assoc 97:523–534
Hayashi F (1985) Corporate finance side of the Q theory of investment. J Public Econ 27:261–280
Henderson DJ, Parmeter CF (2015) Applied nonparametric econometrics. Cambridge University Press, Cambridge
Henderson DJ, Parmeter CF, Kumbhakar SC (2012) A simple method to visualize results in nonlinear regression models. Econ Lett 117(4):578–581
Huang CJ, Liu J-T (1994) Estimation of a non-neutral stochastic frontier production function. J Prod Anal 5(1):171–180
Jondrow J, Lovell CAK, Materov IS, Schmidt P (1982) On the estimation of technical efficiency in stochastic frontier production models. J Econ 19(1):233–238
Kaplan SN, Zingales L (1997) Do investment-cash flow sensitivities provide useful measures of financing constraints. Q J Econ 112:169–215
Kaplan SN, Zingales L (2000) Investment-cash flow sensitivities are not valid measures of financing constraints. Q J Econ 115:707–712
Kim W, Linton OB, Hentgartner NW (1999) A computationally efficient oracle estimator for additive nonparametric regression with bootstrap confidence intervals. J Comput Graph Stat 8(2):278–297
Kneip A, Simar L, Van Keilegom I (2015) Nonparametric least squares methods for stochastic frontier models. J Econ 184:379–393
Kumbhakar SC, Ghosh S, McGuckin JT (1991) A generalized production frontier approach for estimating determinants of inefficiency in US diary farms. J Bus Econ Stat 9(1):279–286
Kumbhakar SC, Lovell CAK (2000) Stochastic frontier analysis. Cambridge University Press, Cambridge
Kumbhakar SC, Park BU, Simar L, Tsionas EG (2007) Nonparametric stochastic frontiers: a local maximum likelihood approach. J Econom 137(1):1–27
Li Q (1996) On the root-N-consistent semiparametric estimation of partially linear models. Econ Lett 51(2):277–285
Li Q, Racine J (2007) Nonparametric econometrics: theory and practice. Princeton University Press, Princeton
Li Q, Wang S (1998) A simple consistent bootstrap test for a parametric regression function. J Econom 87(2):145–165
Li Q, Wooldridge J (2000) Estimating semiparametric econometric models by local linear method: with an application to cross country growth. Ann Econ Financ 1(2):337–357
Linton OB, Nielsen JP (1995) A kernel method of estimating structured nonparametric regression based marginal integration. Biometrika 82(1):93–100
Martins-Filho CB, Yao F (2015) Semiparametric stochastic frontier estimation via profile likelihood. Econom Rev 34:413–451
Meeusen W, van den Broeck J (1977) Efficiency estimation from Cobb–Douglas production functions with composed error. Int Econ Rev 18(2):435–444
Parmeter CF, Kumbhakar SC (2014) Efficiency analysis: a primer on recent advances. Found Trends Econom 7(3–4):191–385
Reifschneider D, Stevenson R (1991) Systematic departures from the frontier: a framework for the analysis of firm inefficiency. Int Econ Rev 32(1):715–723
Robinson PM (1988) Root-n consistent semiparametric regression. Econometrica 56:931–954
Schmidt P (2011) One-step and two-step estimation in SFA models. J Prod Anal 36(2):201–203
Simar L, Lovell CAK, van den Eeckaut P (1994) Stochastic frontiers incorporating exogenous influences on efficiency. Discussion Papers No. 9403, Institut de Statistique, Universite de Louvain
Simar L, Van Keilegom I, Zelenyuk V (2014) Nonparametric least squares methods for stochastic frontier models. Center for efficiency and productivity analysis, Working Paper Series No. WP03/2014
Simar L, Wilson PW (2007) Estimation and inference in two-stage, semi-parametric models of production processes. J Econom 136(1):31–64
Simar L, Wilson PW (2010) Inferences from cross-sectional, stochastic frontier models. Econom Rev 29(1):62–98
Tran KC, Tsionas EG (2009) Estimation of nonparametric inefficiency effects stochastic frontier models with an application to British manufacturing. Econ Model 26:904–909
Waldman DM (1982) A stationary point for the stochastic frontier likelihood. J Econom 18(1):275–279
Wang H-J (2002) Heteroscedasticity and non-monotonic efficiency effects of a stochastic frontier model. J Prod Anal 18(2):241–253
Wang H-J (2003) A stochastic frontier analysis of financing constraints on investment: the case of financial liberalization in Taiwan. J Bus Econ Stat 21:406–419
Wang H-J, Schmidt P (2002) One-step and two-step estimation of the effects of exogenous variables on technical efficiency levels. J Prod Anal 18:129–144
Wollni M, Brümmer B (2012) Productive efficiency of speciality and conventional coffee farmers in Costa Rica: accounting for technological heterogeneity and self-selection. Food Policy 37(1):67–76
Acknowledgment
We thank the guest editors as well as three anonymous referees for numerous comments, insights and criticisms that led to a substantially improved version of the manuscript. We are also thankful for feedback received at numerous departmental seminars, conferences and workshops. All remaining errors are ours alone.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interests.
Appendices
Appendix 1: Theoretical properties of the proposed estimator
Here we discuss the necessary conditions to establish \(\sqrt n \) consistency of the estimator for the parametric stochastic frontier as well as the nonparametric component, along with its derivatives.
Assumption 1
The triplets (Y i , X i , Z i ) are independent and identically distributed with E|X−ξ| 4+δ < ∞ for δ > 0 where ξ = E[X|Z]. Further, E[Y|X,Z] = X′β−g(Z), ∀ X, Z.
Assumption 2
ε⊥X, Z and E[ε 2] = σ 2(X, Z) < ∞.
Assumption 3
\(f(Z) \in {\cal G}_\lambda ^\infty \) where \(\lambda > 0;\xi \in {\cal G}_\mu ^2\) , where μ > 0; \(g(Z) \in {\cal G}_\nu ^4\) , where \(\nu > 0\) . Here \({\cal G}_b^a\) is the class of functions whose elements are b-times differentiable with derivatives bounded by a function whose has ath-order finite moments.
Assumption 4
For n → ∞, h → 0, nh 4ν → 0 and n 1−δ h 2q → ∞ for some δ > 0.
Assumption 5
The kernel weighting function \(k( \cdot )\) is such that \(k \in {{\cal K}_\nu }\) , where \({{\cal K}_\nu }\) , \(\nu \ge 1\) is the class of even functions which satisfy \({\int} {s^i}k(s)ds = {\delta _{i0}}\) for \(i = 0, \ldots ,\nu - 1\) where δ i0 is Kronecker’s delta and \(k(s) = O\left( {{{(1 + |s{|^{\nu + 1 + \delta }})}^{ - 1}}} \right)\) for some δ > 0.
Given that ε will have higher moments which depend on z, we allow for arbitrary heteroskedasticity in Assumption 2. We impose standard assumptions (in the context of the theory for partly linear regression) on the differentiability of the unknown function, the density of z, and the kernel function. One difference with these results is the requirement that v = X − ξ has finite fourth moment as well as ε having finite fourth moment. Robinson (1988) only requires finite second moments, but to allow for arbitrary heteroskedasticity these moment conditions need to be strengthened. Assumption 5 restricts the kernel to be a bounded, νth-order kernel and is equivalent to Definition 1 in Robinson (1988).
These conditions mimic those found in Li (1996) and this allows a generalization of Robinson (1988) main result to allow use of a second order kernel for dimension up to 5. Lastly, here we are following the approach of Fan et al. (1995) and using density weighted demeaned variables to avoid trimming. Similar assumptions are used by Tran and Tsionas (2009) and Gao et al. (2015) except that they allow for different first and second stage bandwidths. Here we are generically using the same bandwidth everywhere, but one could allow different bandwidths for each separate conditional mean that is estimated. This would require additional notation as well as assumptions on the rate of decay of both sets of bandwidths.
Theorem 1
Under Assumptions 1–4 we have that
where Ω1 = Φ−1ΨΦ−1 with \(\Phi = E[{\varphi _i}{\varphi '_i}]\), \(\Psi = E[{\sigma ^2}({x_i},\,{z_i}){\varphi _i}{\varphi '_i}]\) and φ i = x i −ξ i .
The proof of Theorem 1 can be found in Li (1996). This result provides \(\sqrt n \)-asymptotic normality for the estimator of the parametric component of the partly linear regression model as well as offering an avenue for conducting inference. Given the presence of the unknown variance term, a resampling algorithm, such as residual resampling, might be warranted to construct the variance–covariance matrix.
Before discussing the asymptotic normality of the kernel estimator of conditional inefficiency, we introduce some additional notation. First, use \({R_k} = {\int} {k^2}(u)du\) to denote the roughness of the kernel, \({c_k} = {\int} {u^2}k(u)du\) to capture the variance of the kernel, \({\nu _k} = {\int} {u^2}{k^2}(u)du\), and μ k (x) = 0.5c k tr{g(2)(z)}, to signify the sum of second derivatives, scaled the by the kernel’s variance of the unknown conditional inefficiency function. Lastly, let 0 q denote a zero vector of length q and I q an identity matrix of dimension q.
Theorem 2
Under Assumptions 1–4, if f(z) > 0,
where
and
The proof of Theorem 2 appears in Li and Wooldridge (2000). The form of D(n) makes clear the slow rate of convergence of the estimator of the conditional mean of inefficiency as well as the first derivatives. As the dimensionality of Z increases the rate of convergence decreases, the well known ‘curse of dimensionality’ that many nonparametric estimators suffer from. It should be noted that despite the slow rate of convergence, the estimator is consistent and these rates are as fast as possible for the set of assumptions used here.
Appendix 2: Theoretical properties of the proposed test
Here we discuss the necessary conditions to establish the asymptotic normality of the test statistic proposed in (10).
Assumption 6
The triplets (Y i , X i , Z i ) are independent and identically distributed. (X, Z) has support \({\cal L}\) that is convex in z and admits a density function f(x, z). E|Y|4 < ∞.
Assumption 7
\(\tilde \gamma - \gamma = {O_p}({n^{ - 1/2}})\) under H 0 while \(\hat \beta - \beta = {O_p}({n^{ - 1/2}})\) under either H 0 or H 1.
Assumption 8
∇g(x,·) and ∇2 g(x,·) are continuous in x and dominated by functions with finite second moments. f(x, z), E[ε 2|X = x, Z = z] = σ 2(x, z) and E[ε 4|X = x, Z = z] = μ 4(x, z) all satisfy the Lipschitz condition: \(|m(x,\,z + \upsilon ) - m(x,\,z)| \le G(x,\,z)||\upsilon ||\) with \(E\left[ {{G^2}(X,\,Z)} \right] < \infty \)
Assumption 9
As n → ∞, h → 0 and nh q → ∞.
Assumption 10
The kernel function is nonnegative, bounded and symmetric. Further, \({\int} k(u)du = 1\) .
Assumptions 6–10 are relatively weak. The support condition could be the entire Euclidean space \({{\Bbb R}^q}\) or a compact subset. Even in the case of a compact subset no knowledge of the boundary is required and the assumptions do not require that 0 < f(x,z) at the boundary. Assumption 7 requires that we use \(\sqrt n \)-consistent estimators for both β and γ. If a nonlinear least squares estimator is deployed to estimate the fully parametric model this assumption is trivially satisfied.
Theorem 3
Under Assumptions 6–10 we have
-
(1)
Under H 0, as n → ∞
$$n{h^{q/2}}{I_n}/\sqrt {\hat \Omega \,} \mathop { \to }\limits^D \,N(0,\,1),$$(20)where \(\hat \Omega \, = \,(1/{n^2}{h^q})\mathop{\sum}\nolimits_{i = 1}^n \mathop{\sum}\nolimits_{j = 1,j \ne i}^n \varepsilon _i^2\varepsilon _j^2{K_h}({Z_i},\,{Z_j})\) is a consistent estimator of Ω and ε = Y−X′β − g(Z, γ).
-
(2)
Under H 1, \(Pr(n{h^{q/2}}{I_n}/\sqrt {\hat \Omega } > {B_n})\, \to \,1\) for any nonstochastic sequence \({B_n}\, = \,o(n{h^{q/2}})\).
See Li and Wang (1998) for a proof of Theorem 3. Theorem 3 demonstrates that the use of a normalized version of I n produces a test statistic that is asymptotical normal under H 0 and has power in all directions, making it a consistent test.
Appendix 3: Extension to an additive nonparametric setup
The additive model would look like
where \({\varepsilon _i} = {v_i} - \left( {{u_i} - g({Z_i})} \right)\) and \(g({Z_i}) = E[{u_i}|{Z_i}]\). Several alternative approaches to estimate additive models exist, including global approximation (splines, series, sieves, etc.) and local approximation methods (kernel smoothing). The most common kernel-based methods, consistent with the discussion in our paper, include marginal integration (Linton and Nielsen 1995) and backfitting (Buja et al. 1989). We could also use the oracle estimator of Kim et al. (1999).
If we estimate the conditional mean of y given X in a nonparametric fashion, we have that, for a constant c,
The final term E[g(Z)|X] introduces a bias. In order to eliminate this bias, Kim et al. (1999) propose an instrument function, w(X, Z), such that
If we have such an instrument, then it can be shown that
The exact instrument proposed is
where \({f_X}\left( X \right)\), \({f_Z}\left( Z \right)\) and \(f\left( {X,Z} \right)\) are the marginal and joint probability densities of X and Z, respectively. We can think of these instruments as a measure of the degree of independence between the two sets of regressors, X and Z, influencing the two objects of interest, the frontier and the mean of inefficiency. Note that in the simple case where X is independent from Z, \(w( \cdot , \cdot )\, = \,1\). This has intimate connections to the construction of the copula function.w(X, Z) is a valid instrument given that
and
In practice, we estimate the instruments with standard kernel density estimators. We estimate (22) by choosing a method which eliminates the random denominator term. Formally, if we have \(n\) observations for Y, X and \(Z\), \(\left\{ {{Y_i},{X_i},{Z_i}} \right\}_{i = 1}^n\), our estimator of (22), which we define as \({\gamma _m}\left( \cdot \right)\), is
where \(K_{ij}^X\) is the product kernel with bandwidth h X for X and the kernel estimators of the marginal and joint densities are
and
Each element of \({\hat \gamma _g}\left( Z \right)\) is similarly estimated. The first stage estimator of γ g (Z) (at the point Z i ) is
Appendix 4: Enforcing positivity on the estimated mean of inefficiency
Du et al. (2013) have proposed a general methodology for imposing various smoothness constraints on an estimated nonparametric regression surface. Here, our smoothness constraints are on the boundedness of the function itself as opposed to ensuring monotonicity or concavity, say. To begin, note that the estimator in (9) can be written as
which highlights that each observation in the sum contributes uniformly to the estimator of g(Z i ). The idea of Du et al. (2013) is to replace the uniform 1/n weights with weights selected to ensure that the constraint of interest is satisfied, here nonnegativity. Thus, we have the constraint weighted estimator
where the p j s are selected such that \(\hat g({Z_i}) \ge 0\) for every Zj. The weights can be selected by minimizing some distance metric between the uniform weights and the constraint weights. Du et al. (2013) recommend that L 2 metric, \(D(p)\, = \,({p_u} - p)\prime ({p_u} - p)\), which then suggests that the weights, p, should be selected that minimize D(p) subject to \(\hat g(z) \ge 0\); as it turns out this is a quadratic programming problem.
The procedure to estimate the original model is to use the kernel methods to estimate \(E[{Y_i}|{Z_i}]\) and \(E[{X_i}|{Z_i}]\) and use these estimated conditional means to obtain consistent estimates of β. Then, construct \({\tilde \varepsilon _i}\) and use the local linear estimator in (9) to estimate g(Z i ). If the unconstrained estimates satisfy nonnegativity then proceed to direct analysis of the marginal effects of each of the determinants. If the constraints are not satisfied globally then use the constrained kernel regression procedure described above to impose the constraints prior to investigating the marginal impact of each of the determinants of inefficiency. This procedure works because of the \(\sqrt n \)-consistency of the OLS estimator established in Theorem 1. Thus, the main results of Du et al. (2013) hold even though a first stage estimation was conducted.
Rights and permissions
About this article
Cite this article
Parmeter, C.F., Wang, HJ. & Kumbhakar, S.C. Nonparametric estimation of the determinants of inefficiency. J Prod Anal 47, 205–221 (2017). https://doi.org/10.1007/s11123-016-0479-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-016-0479-x