Abstract
This paper considers the estimation of Kumbhakar et al. (J Prod Anal. doi:10.1007/s11123-012-0303-1, 2012) (KLH) four random components stochastic frontier (SF) model using MLE techniques. We derive the log-likelihood function of the model using results from the closed-skew normal distribution. Our Monte Carlo analysis shows that MLE is more efficient and less biased than the multi-step KLH estimator. Moreover, we obtain closed-form expressions for the posterior expected values of the random effects, used to estimate short-run and long-run (in)efficiency as well as random-firm effects. The model is general enough to nest most of the currently used panel SF models; hence, its appropriateness can be tested. This is exemplified by analyzing empirical results from three different applications.




Similar content being viewed by others
Notes
For a survey of efficient numerical and Monte Carlo methods to compute multi-normal integrals, see Genz and Bretz (2009).
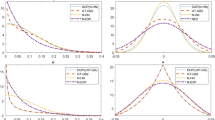
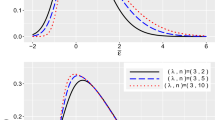
Results reported here are not from detailed MC simulations. The idea is to show some results from two simulations to show the superiority of the ML approach.
The data-generating process is as follows: we get b i from a N(0, σ 2 b ), u i0 from a N +(0, σ 21u ), u it from a N +(0,σ 22u ) and ε it from a N(0,σ 2 e ). Finally, y it is obtained from y it = β0 + b i + u i0 + u it + ε it .
However, the KLH method of estimation can provide good starting values for the parameters that have to be estimated maximizing the log-likelihood (5). Because maximizing the latter is a time-consuming task, the amount of time required for finding a solution can be greatly reduced by imposing good starting values.
A full description of the data set is provided in Berta et al. (2009).
The data set does not include day-hospital discharges. The case-mix is an index specifying the complexity of a discharge, based on the Diagnosis-Related Group (DRG) classification.
Note that short-run (long-run) inefficiency can be viewed as 1 minus short-run (long-run) efficiency. Conversely, inefficiency = 1 − efficiency.
This comparison can be done with other models as well. Because the TTF model is widely used in practice we limit our comparison to just the TTF and TTT models.
The data were collected by the International Rice Research Institute. Details of the survey are provided by Pandey et al. (1999).
Details on these results can be obtained from the authors upon request.
The features of the data set are presented in Malighetti et al. (2007).
References
Aigner D, Lovell CAK, Schmidt P (1977) Formulation and estimation of stochastic frontier production function models. J Econom 36:21–37
Arellano-Valle E, Bolfarine H, Lachos H (2005) Skew-normal linear mixed models. J Data Sci 3:415–438
Arellano-Valle E, Azzalini A (2006) On the unification of families of skew-normal distributions. Scand J Stat 33:561–574
Battese GE, Coelli TJ (1988) Prediction of firm-level technical efficiencies with a generalized frontier production function and panel data. J Econom 38:387–399
Battese GE, Coelli TJ (1992) Frontier production functions, technical efficiency and panel data: with applications to paddy farmers in India. J Prod Anal 3:153–169
Berta P, Callea G, Martini G, Vittadini G (2009) The effects of upcoding, cream skimming and readmissions on the Italian hospitals efficiency: a population-based investigation. Econ Model 27:812–821
Cartinhour J (1990) One-dimensional marginal density functions of a truncated multivariate normal density function. Commun Stat A Theor 19:197–203
Chen YY, Schmidt P, Wang HJ (2011) Consistent estimation of the fixed effects stochastic frontier model, unpublished manuscript
Coelli T, Henningsen A (2010) Frontier: stochastic frontier analysis. R package version 0.996-6. http://www.R-project.org
Coelli T, Rao D, O’Donnell C, Battese GE (2005) An introduction to efficiency and productivity analysis. Springer, New York
Colombi R, Martini G, Vittadini G (2011) A stochastic frontier model with short-run and long-run inefficiency random effects. Aisberg, WP 012011, Università degli studi di Bergamo, Italy. http://aisberg.unibg.it/handle/10446/842
Cornwell C, Schmidt P, Sickles R (1990) Production frontiers with cross-sectional and time-series variation in efficiency levels. J Econom 46:185–200
Dominguez-Molina A, Gonzales-Farias G, Ramos-Quiroga R (2004) Skew normality in stochastic frontier analysis. In: Genton M (ed) Skew elliptical distributions and their applications. Chapman and Hall CRC, London
Farsi M, Filippini M, Greene W (2005) Efficiency measurement in network industries: application to the Swiss railway companies. J Regul Econ 28:69–90
Genz A, Bretz F (2009) Computation of multivariate normal and t probabilities. Springer, New York
Gonzáles-Farías G, Domínguez Molina A, Gupta A (2004) Additive properties of skew normal random vectors. J Stat Plan Infer 126:521–534
Greene W (2005a) Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J Econom 126:269–303
Greene W (2005b) Fixed and random effects in stochastic frontier models. J Prod Anal 23:7–32
Greene W (2009) The econometric approach to efficiency analysis, chapter 2. In: Fried HO, Lovell CAK, Schmidt SS (eds) The measurement of productive efficiency—techniques and applications, Oxford University Press, Oxford, pp 92–251
Horrace WC (2005) Some results on the multivariate truncated normal distribution. J Multivar Anal 94:209–221
Jondrow J, Lovell CAK, Materov IS, Schmidt P (1982) On the estimation of technical inefficiency in the stochastic frontier production function model. J Econom 19:233–238
Kumbhakar SC (1987) The specification of technical and allocative inefficiency in stochastic production and profit frontiers. J Econom 34:335–348
Kumbhakar SC (1990) Production frontiers, panel data and time-varying technical inefficiency. J Econom 46:201–211
Kumbhakar SC, Hjalmarsson L (1993) Technical efficiency and technical progress in Swedish dairy farms. In: Fried HO, Lovell CAK, Schmidt SS (eds) The measurement of productive efficiency—techniques and applications, Oxford University Press, Oxford, pp 256–270
Kumbhakar SC, Heshmati A (1995) Efficiency measurement in Swedish dairy farms: an application of rotating panel data, 1976–1988. Am J Agr Econ 77:660–674
Kumbhakar SC, Hjalmarsson L (1995) Labour-use efficiency in Swedish social insurance offices. J Appl Econom 10:33–47
Kumbhakar SC, Lovell CAK (2000) Stochastic frontier analysis. Cambridge University Press, Cambridge
Kumbhakar SC, Wang HJ (2005) Estimation of growth convergence using a stochastic production frontier approach. Econ Lett 88:300–305
Kumbhakar SC, Lien G and Hardaker JB (2011) Technical efficiency in competing panel data models: a study of Norwegian grain farming. 2011 International Congress of the European Association of Agricultural Economists, Zurich
Kumbhakar SC, Lien G and Hardaker JB (2012) Technical efficiency in competing panel data models: a study of Norwegian grain farming. J Prod Anal. doi:10.1007/s11123-012-0303-1
Lee Y, Schmidt P (1993) A production frontier model with flexible temporal variation in technical inefficiency. In: Fried H, Lovell K (eds) The measurement of productive efficiency: techniques and applications, Oxford University Press, New York
Lin T, Lee C (2008) Estimation and prediction in linear mixed models with skew-normal random effects for longitudinal data. Stat Med 27:1490–1507
Malighetti P, Martini G, Paleari S, Redondi R (2007) An empirical investigation on the efficiency, capacity and ownership of Italian airports. Rivista di Politica Econ 47:157–188
Meeusen W, van den Broeck J (1977) Efficiency estimation from Cobb-Douglas production functions with composed Error. Int Econ Rev 18:435–44
Pandey S, Masicat P, Velasco L, Villano R (1999) Risk analysis of the rainfed rice production system in Tarlac, Central Luzon, Philippines. Exp Agric 35:225–237
Pitt M, Lee L (1981) Measurement of sources of technical inefficiency in the Indonesian weaving industry. J Dev Econ 9:43–64
R Development Core Team (2009) R: A language and environment for statistical computing. R Foundation for Statistical Computing. ISBN 3-900051-07-0. http://www.R-project.org
Schmidt P, Sickles R (1984) Production frontiers and panel data. J Bus Econ Stat 2:367–374
Silvapulle M, Sen P (2005) Constrained statistical inference. Wiley, Hoboken, NJ
Wang HJ, Ho CW (2010) Estimating fixed-effect panel data stochastic frontier models by model transformation. J Econ 157:286–296
Acknowledgments
Gianmaria Martini acknowledges financial support from the Università di Bergamo (Grant 60MART09). Giorgio Vittadini acknowledges financial support from the Italian Ministry of University (MUR), CRISP and Lombardia Informatica.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Proposition 1
In the TTT SF model presented in Eq. (1), the random components b i − u i0 − u it + e it can be written as the sum of the time-independent terms (i.e., η i = b i − u i0) and of the time-dependent terms (i.e., ɛ it = e it − u it ). According to our assumptions, these two terms are independent in probability and are given by the difference of a normal-random variable and an independent, left-truncated-at-zero normal random variable. It is well known (Kumbhakar and Lovell 2000) that η i has the following density:
Analogously, the density of ɛ it (t = 1, 2, …, T) is:
The previous two densities are (1,1) closed-skew normal densities and so the random components b i − u i0 − u it + e it of the vector \({\bf 1}_T b_i+\user2{Au}_i+\user2{e}_i=-\user2{A}(\eta_{i}, \varepsilon_{i1}, \dots, \varepsilon_{iT})^{'}\) are sums of two closed-skew normal random errors.
Let \(\varvec{\Upupsilon}\) be the diagonal matrix with the ratios \(\frac{\sigma_{2u,t}^2}{\sigma_{e}^2+\sigma_{2u,t}^2}\) on the main diagonal. From Theorem (3) of Gonzáles-Farías et al. (2004), it follows that the T + 1 independent-random variables η i , ɛ it (t = 1, 2, …, T) have a joint (T + 1,T + 1) closed-skew normal density function with parameters \(\varvec{\nu}_0={\bf 0}, \varvec{\mu}_0= {\bf 0}\), and
Finally, from the previous result and from Theorem (1) of Gonzáles-Farías et al. (2004), it follows that the T dimensional-random vector \({\bf 1}_T b_i+ \user2{Au}_i +\user2{e}_i=-\user2{A}(\eta_{i}, \varepsilon_{i1}, \dots, \varepsilon_{iT})^{'}\) with components \(b_{i}-u_{i0}-u_{it}+e_{it}=\eta_{i}+\varepsilon_{it}\) has a (T,T + 1) closed-skew normal distribution with parameters \(\varvec{\nu}={\bf 0}, \varvec{\mu}= {\bf 0}, \varvec{\Upgamma}= \user2{A}\varvec{\Upgamma}_0 \user2{A}^{\prime} =\varvec{\Upsigma} +\user2{AV}\,\user2{A}^{\prime}, \user2{D}=-\user2{D}_0 \varvec{\Upgamma}_0 \user2{A}^{\prime} \varvec{\Upgamma}^{-1}= \user2{R}, \varvec{\Updelta}=\varvec{\Updelta}_0+\user2{D}_0 \varvec{\Upgamma}_0\user2{D}^{\prime}_0-\user2{D}_0 \varvec{\Upgamma}_0\user2{A}^{\prime} \varvec{\Upgamma}^{-1} \user2{A} \varvec{\Upgamma}_0 \user2{D}^{\prime}_0= \varvec{\Uplambda}\). Because \(\varvec{\mu}\) is a location parameter and \(\user2{y}_i= {\bf 1}_T \beta_0+ \user2{X}_i\varvec{\beta} +{\bf 1}_T b_i+\user2{Au}_i +\user2{e}_i\), the statement of the Proposition follows.
Proof of Proposition 3
To prove b) note that:
where the third equality follows from Lemma 2 of Arellano et al. (2005). Noting that \(f(\user2{u}_i|\user2{y}_i)\) is the density of a left-truncated-at-zero multi-normal random variable, d) follows from Lemma 13.6.1 of Dominguez-Molina et al. (2004). To prove a) we observe that:
Point a) of the proposition follows immediately. Observing that \(f(b_i|\user2{y}_i)\) is a closed-skew normal density, point c) follows from the result shown in Eq. (3) on the moment-generating function of a closed-skew normal random variable.
Rights and permissions
About this article
Cite this article
Colombi, R., Kumbhakar, S.C., Martini, G. et al. Closed-skew normality in stochastic frontiers with individual effects and long/short-run efficiency. J Prod Anal 42, 123–136 (2014). https://doi.org/10.1007/s11123-014-0386-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-014-0386-y