Data aggregation in stochastic frontier models: the closed skew normal distribution

Abstract

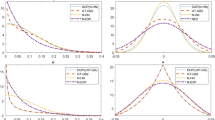
The effect of aggregation on estimates of stochastic frontier functions is considered. Inefficiency is assumed associated with the individual units being aggregated. In this case, the aggregated data have a closed skew normal distribution. Estimating the parameters of a closed skew normal distribution is difficult and so we focus mostly on the biases created by ignoring the fact that the data are aggregated. The conclusions are based on both analytical and Monte Carlo results. When data for firms are aggregates over smaller units and the inefficiency is associated with the units and not the firm, empirical work that does not consider the effect of aggregation will attribute the inefficiency of large firms to diseconomies of scale.

Appendix

This appendix shows how to derive the distribution of aggregated data when a firm-level random effect and a firm-level inefficiency term are added to Eq. (7). With the two extra terms, the cost function becomes

$$ C_{ij} = {\mathbf{x}}_{ij}{\varvec{\upbeta}} + w_{ij} + v_{ij} +\gamma_{j} + \lambda_{j}$$

(21)

where $\gamma_{j} \sim iid N\left( {\nu ,\sigma_{\gamma }^{2} }\right), \lambda_j \sim iid \left| {N\left( {\nu ,\sigma_{\lambda}^{2} } \right)} \right|, \quad \text{cov} (\gamma_{j},\lambda_{j} ) = 0$ and $\gamma_{j} \, {\text{and}}\, \lambda_{j}$ are independent of $w_{ij} \, {\text{and}}\, \nu_{ij} .$ The average cost function in Eq. (8) then becomes

$$ {\text{AC}}_{i} = {\mathbf{x}}_{ \cdot }^{\prime } {\varvec{\upbeta}} + (w_{ \cdot j} + \nu_{ \cdot j} ) + \gamma_{j} + \lambda_{j} . $$

(22)

The term $(w_{ \cdot j} + v_{ \cdot j} )$ follows a closed skew normal distribution as defined in (15). The term $(\gamma_{i} + \lambda_{j} )$ follows a closed skew normal distribution as in (12):

$$ (\gamma_{j} + \lambda_{j} ) \sim {\text{CSN}}_{1,1} \left( {0, \sigma_{\gamma }^{2} + \sigma_{\lambda }^{2} ,\frac{{\sigma_{\lambda }^{2} }}{{\sigma_{\gamma }^{2} + \sigma_{\lambda }^{2} }},0, \frac{{\sigma_{\gamma }^{2} \sigma_{\lambda }^{2} }}{{\sigma_{\gamma }^{2} + \sigma_{\lambda }^{2} }}} \right) $$

(23)

The terms $(w_{ \cdot j} + v_{ \cdot j} )$ and $(\gamma_{j} + \lambda_{j} )$ are defined to be independent. Since they are independent their sum must also follow a closed skew normal distribution by Theorem 4 in Gonzales-Farias et al. (2004). The distribution of their sum is

$$ \left( {w_{ \cdot j} + v_{ \cdot j} } \right) + \left( {\gamma_{j} + \lambda_{j} } \right)\sim CSN_{1, n + 1} \left( {\left( {0, \frac{1}{n}(\sigma_{w}^{2} + \sigma_{v}^{2} } \right) + \sigma_{\gamma }^{2} + \sigma_{\lambda }^{2} , D^{M} , {\mathbf{0}}_{{\user2{n} + {\mathbf{1}}}} , {{\Updelta}}^{M} } \right) $$

(24)

where ${\mathbf{0}}_{{\user2{n} + {\mathbf{1}}}}$ is a n × 1 vector of zeroes, D ^M is $\left[ {\sigma_{v}^{2} {\mathbf{1}}_{\user2{n}}^{'} , n\sigma_{\lambda }^{2} } \right] \cdot \left( {\sigma_{w}^{2} + \sigma_{v}^{2} + n\sigma_{\gamma }^{2} + n\sigma_{\lambda }^{2} } \right)^{ - 1}$ and Δ^M can be derived following Theorem 4 in Gonzalez-Farias et al. and their n = 2 example. While it is possible to derive the distribution, estimating the parameters of such a distribution for a realistic problem with several explanatory variables is not an easy task. Note that in some instances, disaggregate data may be available. Estimating the parameters with disaggregate data still has estimation difficulties since the disaggregate data also follow a closed skew normal distribution. Colombi (2010) has suggested a two-step procedure for estimating the disaggregate model. Greene (2005) uses simulated maximum likelihood to estimate fixed effect and random effects stochastic frontier models with only one of the two possible inefficiency terms. Researchers have also suggested maximum likelihood procedures using the EM algorithm with general skew normal distributions and mixed models, but with only the firm-level random effect (Lin 2009; Lachos et al. 2010).