Robust network pricing and system optimization under combined long-term stochasticity and elasticity of travel demand

Abstract

Network pricing serves as an instrument for congestion management, however, agencies and planners often encounter problems of estimating appropriate toll prices. Tolls are commonly estimated for a single-point deterministic travel demand, which may lead to imperfect policy decisions due to inherent uncertainties in future travel demand. Previous research has addressed the issue of demand uncertainty in the pricing context, but the elastic nature of demand along with its uncertainty has not been explicitly considered. Similarly, interactions between elasticity and uncertainty of demand have not been characterized. This study addresses these gaps and proposes a framework to estimate nearest optimal first-best tolls under long-term stochasticity in elastic demand. We show first that the optimal tolls under the deterministic-elastic and stochastic-elastic demand cases coincide when cost and demand functions are linear, and the set of equilibrium paths is constant. These assumptions are restrictive, so three larger networks are considered numerically, and the subsequent pricing decisions are assessed. The results of the numerical experiments suggest that in many cases, optimal pricing decisions under the combined stochastic-elastic demand scenario resemble those when demand is known exactly. The applications in this study thus suggest that inclusion of demand elasticity offsets the need of considering future demand uncertainties for first-best congestion pricing frameworks.

Introduction and background

Congestion pricing

Road pricing or tolling strategies have traditionally been mechanisms to generate revenues for undertaking new infrastructure projects and for the upkeep and maintenance of current ones. However, these strategies are also common means of mitigating and managing congestion on road networks, which are referred to as congestion pricing strategies with ‘system performance’ objectives. Numerous studies including May and Milne (2000), Ho et al. (2005), Liu et al. (2010), Kockelman and Lemp (2011) and Watling et al. (2015); among many others, have explored congestion pricing schemes in which tolls can optimize system performance by alleviating congestion. Researchers have recently identified implications of congestion pricing in the context of automonous vehicles (Le Vine and Polak 2016; Bansal and Kockelman 2016). Congestion pricing incentivizes the users in a way that their route choices coincide with the system optimal routes and thus the transportation system operates at its optimal state.

In theory, congestion pricing has been classified as ‘first’ and ‘second’ best pricing. This paper focuses on first-best pricing strategies that allow setting tolls on all links in the network. Some of the earliest research discussing first-best pricing models include Pigou (1920) and Knight (1924). Second-best pricing strategies aim at levying tolls only on certain links of the network, most likely congestion-prone ones. Besides, second-best pricing is adopted when there are political and societal conflicts associated with tolling certain links or corridors. Readers are directed to Yang and Huang (2005) and Verhoef (2000) for a more detailed discussion on the theoretical foundations of congestion pricing.

This paper is concerned with system performance objectives of first-best tolling strategies, primarily aimed at mitigating network congestion regardless of its revenue generation aspects. Recent years have seen numerous implementations of congestion pricing schemes worldwide—such as the electronic road pricing (ERP) scheme in Singapore, London congestion charge, the pilot electronic toll collection scheme in Hong Kong, and the Stockholm congestion tax, to name a few, mostly locations where network capacity expansion is not feasible.

Travel demand uncertainty

In implementing the above-noted pricing schemes, transportation agencies conventionally set tolls on the basis of a single-point forecasted future demand on the network. Approaches have been proposed for finding tolls for single-point forecasted or fixed demand values (Hearn et al. 2001). Travel demand is a critical factor in assessing the system performance. However, it is unlikely that the system will encounter the exact forecasted demand in future, not solely because of inherent uncertainties in it, but due to various factors such as land use changes, demographic shifts, taste variations of commuters, economic trends, and so forth (Duthie and Waller 2006). Also, regional population variations and fuel-price changes are some other reasons that can make accurate predictions of future demands practically impossible (Gardner et al. 2011). Thus essentially, future demand cannot be simply assumed to be ‘deterministic’. It is thus critical that instead of adopting a deterministic pricing model, neglecting potential uncertainties in demand, planners and policymakers should rather adopt a robust and a more realistic model. The model should be able to optimize the system performance for a range of future demand scenarios and not just for the single-point forecasted demand. Incorporating the element of uncertainty in long-term demand can be indispensable in the system and network-based decisions such as capacity improvements or congestion pricing schemes, which are meant to serve a forecasted future demand.

Some past studies investigated the issues associated with the toll estimation based on single-point demand forecasts and also proposed potential approaches to incorporate demand uncertainties in the pricing frameworks. Some early studies in the domain of pricing under demand uncertainty include Kraus (1982), which investigated optimal freeway tolls and capacities under demand uncertainty. Along similar lines, d’Ouville and McDonald (1990) analytically examined the effects of uncertain demand on optimal highway network capacity and congestion tolls. Raman and Chatterjee (1995) evaluated demand uncertainty in a broader context of a general economic market containing a monopolist producer and uncertain dynamics of user-end demand and examine the optimal pricing structure. A study by Gardner et al. (2008) proposed a first-best tolling framework to find nearest optimal tolls considering long-term stochasticity in the demand. It concluded that toll setting based on the deterministic value of demand may worsen the system performance if the real future demand considerably deviates from the forecasted demand. Waller et al. (2001) asserted that system-based decisions such as capacity expansion or pricing based on a single-point deterministic demand may overestimate system performance. Wang et al. (2013) formulated a global optimization method for finding second best tolls considering long-term demand uncertainty. Chen and Subprasom (2007) investigated a build-operate-transfer (BOT) scheme based private toll regulations and take into account demand uncertainties. Nagae and Akamatsu (2006) used stochastic singular control programming for the optimal toll setting problem and uniquely considered the demand to be a stochastic differential equation. Li et al. (2007) utilized pricing frameworks to improve road network reliability and to optimize system performance (i.e., improve reliability and minimize travel time on a network level). Moreover, they considered day-to-day demand variability rather than long-term planning demand stochasticity in the toll design problem. Such an analysis can be invaluable for developing dynamic or time-of-day pricing strategies, and real-time traffic operations management. Some recent works such as Xu et al. (2016), Rambha and Boyles (2016) and Duell et al. (2014) have also focused on the notion of day-to-day pricing where tolls on a given day are set based on the state of the system on the previous day. Szeto and Wang (2015) explored reliability-based network pricing, while Repolho et al. (2016) approached the pricing problem incorporating combined social welfare and private sector profit objectives. Cheng et al. (2016) reviewed recent developments in the dynamic pricing. This paper, however, is concerned with planning demand uncertainty on a long-term forecast horizon, which is more in line with long-range transportation planning, and decision-making for system optimization using pricing instruments. Chen et al. (2012) conducted an ‘impact area’ vulnerability analysis of link closures and congestion considering demand uncertainty, which is also better-suited for recommending short-term strategies such as day-to-day congestion management, or traffic impact analysis under special event or incident situations.

Research goals and contributions

Many aforementioned studies developed tolling frameworks for deterministic and stochastic demands, however, the elastic nature of demand has not been explicitly considered. Yildirim and Hearn (2005) developed a methodology for finding first-best tolls for a deterministic elastic demand relationship, but demand uncertainty was not accounted for. Wang et al. (2014) solved the first-best pricing problem with elastic demand for multiple classes of travelers, characterized based on their value of time. A theoretical study by Penchina (2003) compared the economic efficiency of different pricing mechanisms (marginal social cost pricing and minimum revenue pricing) on inelastic and elastic demand scenarios.

The current study extends the previous congestion pricing frameworks by integrating stochasticity along with elasticity of demand. Introducing stochastic elements within elastic demand functions can potentially enable agencies to set tolls considering more realistic demand scenarios, both by modeling the responsiveness of demand to network conditions, and possible variability in its forecasted values. This study also investigates the hypothesis that elastic demand functions partially mitigate the effects of long-term demand uncertainty on the system performance. (“Motivation and theoretical basis” section provides discussion on the a priori plausibility of this hypothesis.) This hypothesis is then empirically tested through numerical experiments on networks of various size. In such pricing frameworks that aim to capture demand uncertainty and elasticity, it is important to clearly specify what information is available to each decision-maker when they make their choices. (Boyles et al. 2010). In this study, planners are assumed to know the distribution of future maximum demand and the elastic relationship of actual demand with prevalent network conditions at the time of pricing decisions. Planners can thus estimate first-best static tolls (Ieromonachou et al. 2006; Xu 2009) considering demand elasticity and long-term uncertainty.

Apart from uncertainty in the future travel demand, planners’ decisions also often have unpredictable elements based on their varying levels of risk responsiveness and system characteristics. Risk averse planners are more likely to lay higher emphasis on reducing the variations of system performance rather than its expected value, irrespective of system characteristics. However more commonly, planners aim to maximize the expected value in case of highly robust or steady systems, and minimize all possible fluctuations in system performance in case of volatile systems. In the context of this study, robust systems are classified as ones whose expected performance is not highly sensitive to fluctuations in demand, whereas volatile systems are ones that are relatively sensitive.

Thus, taking into account motivations for more efficient and realistic planning, the specific contributions of this study are as follows:

• 1. Development of a heuristic to find first-best tolls considering long-term stochasticity and elasticity of travel demand as well as accounting for uncertainty in planners’ decisions;

• 2. Characterizing the interaction between uncertainty and elasticity of travel demand in the context of congestion pricing.

• 3. Numerically investigating the hypothesis that demand elasticity offers a restoring mechanism against long-term demand uncertainty in optimal pricing decisions.

As motivation for investigating this hypothesis, we present a theoretical result showing that optimal tolls are unaffected by demand stochasticity, albeit under several restrictive conditions. While these conditions do not hold in general networks, we postulate that the conclusion of this result still is approximately true in larger-scale networks. Therefore, we conduct a series of numerical experiments to investigate the hypothesis in networks where the theoretical result cannot be directly applied. The study achieves the following modeling goals:

• 1. Demonstrating the proposed approach through numerical experiments on networks of various proportions;

• 2. Modeling and assessment of pricing decisions under a diverse set of possible future demand scenarios such as:

  • a. deterministic inelastic demand (called ‘D-ID’ in this study for brevity);

  • b. stochastic inelastic demand or‘S-ID’, considering uniform and normal probability distributions of future demand realizations;

  • c. deterministic elastic demand or ‘D-ED’; and

  • d. stochastic elastic demand or ‘S-ED’, considering uniform and normal probability distributions of future demand realizations as well as linear and exponential elastic demand relationships.

The rest of the paper is organized as follows. “Motivation and theoretical basis” section develops the basis for studying congestion pricing under combined stochasticity-elasticity of travel demand. “Modeling framework–combined demand elasticity and stochasticity” section describes the components of the proposed congestion pricing heuristic under S-ED scenario. “Model framework demonstration I: Braess network” section demonstrates the developed methodology on the small-scale Braess network. “Model framework demonstration II: Friedrichshain Center, Berlin study area” section expands the implementation of the methodology on the larger Friedrichshain Center network of Berlin, Germany, showing comparable results. “Robust pricing experiment: Sioux Falls study area” section provides another numerical experiment on the Sioux Falls network to further compare optimal congestion pricing policies under different demand scenarios. “Conclusions and future work” section concludes the paper with a summary of the current work along with its implications and relevance to policy and practice, and a discussion of future research avenues.

Motivation and theoretical basis

This section discusses conditions under which the optimal tolls under stochastic and deterministic elastic demand formulations coincide. In the “Appendix”, we show that these tolls coincide in any problem instance satisfying the following conditions (the “Appendix” contains more rigorous phrasings of the conditions which are presented here in intuitive form):

• 1. The link performance functions are linear.

• 2. The demand functions are linear.

• 3. The set of used paths at equilibrium does not depend on the toll or demand realization.

• 4. The deterministic demand forecast is unbiased.

The proof relies on the following logic: under the conditions (1)–(3), the link flows are linear in the uncertain parameter $\epsilon$. As a result, in the expression for traveler surplus, the only terms which are influenced by the tolls are linear in $\epsilon$, and thus depend only on its first moment $E[\epsilon]$. Thus, under the assumption of unbiased forecasts (1), the optimal tolls do not depend on the distribution of $\epsilon$. This suggests that any difference in optimal tolls between the deterministic and stochastic cases must be the result of nonlinear interactions between the tolls and $\epsilon$, in which case the optimal tolls may be influenced by higher-order moments of $\epsilon$. What matters, then, is the degree of nonlinearity in the demand functions and link performance functions in the neighborhood of the deterministic solution. If these functions are approximately linear over the likely range of $\epsilon$, there will likely be little difference in the optimal deterministic and stochastic solutions. On the other hand, if the functions are highly nonlinear, or if typical values of $\epsilon$ are so large that a linear approximation is highly inaccurate, it is possible that the optimal deterministic and stochastic solutions may be substantially different.

The “Appendix” also includes a demonstration of this finding on a small network containing two links, even though the result applies regardless of the size of the network or number of origin–destination demand pairs. In such settings, demand stochasticity still affects the solution in the sense that the expected traveler surplus is different, but the optimal tolling policy remains the same.

These four conditions are strong, and motivate numerical investigation in more realistic networks. It is plausible that these conditions may still hold approximately, even when they do not hold exactly. The first three assumptions are common in the field of equilibrium sensitivity analysis, which and algorithms based on these techniques been successfully applied in network design and other bilevel problems, even in networks with nonlinear cost or demand functions, and where the set of used paths may change (Patriksson 2004; Josefsson and Patriksson 2007; Boyles 2012; Jafari and Boyles 2016). When the network is large, even though the equilibrium path set may change frequently as the demand or tolls are varied, the number of equilibrium paths is large enough that the impact of adding or removing a small number of paths may be insignificant. (Bar-Gera 2006, reports that the equilibrium path set in the Chicago Regional network includes over 93 million paths.) Condition 1 is nothing more than requiring that the demand forecasts are unbiased; clearly, if there is bias in the demand functions then correcting this bias may change the tolls.

Naturally, the proof of such speculation lies in demonstration on more complex, real-world networks with nonlinear travel time and demand functions, and where the set of used paths may vary with demand and tolls. Therefore, after presenting a heuristic for pricing in the elastic demand equilibrium problem with demand uncertainty, the primary analysis of the paper is numerical, and aims to discern which features of this analysis generalize to more realistic networks.

Modeling framework–combined demand elasticity and stochasticity

The current modeling approach for a combined demand elasticity and stochasticity builds up on some earlier first-best tolling frameworks that aim to capture only the long-term demand uncertainty. The framework operates on the principle of deterministic user equilibrium, and under static traffic assignment. The notation to be used in the modeling framework is defined here as follows:

Z ² :

Set of all OD pairs in the network

D _rs :

Demand function for an OD pair (r, s)

D ⁻¹ _rs :

Inverse demand function for an OD pair (r, s)

D ⁻¹ _{rs, SO} :

Inverse demand function at system optimal for an OD pair (r, s)

$\varvec{D}_{{\varvec{SO}}}^{ - 1}$ :

Vector of all inverse demand function values at system optimal

${\mathbf{d}}^{{\varvec{SO}}}$ :

Vector of demand between all OD pairs in the network at system optimal

${\mathbf{D}}$ :

Vector of actual demand between all OD pairs in the network

${\mathbf{d}}^{{{\mathbf{max}}}}$ :

Vector of maximum demand between all OD pairs in the network

${\mathbf{d}}^{{\mathbf{f}}}$ :

Vector of forecasted demand between all OD pairs in the network

d _rs :

Travel demand between an OD pair (r, s)

d ^f _rs :

Forecasted travel demand between an OD pair (r, s)

d ^UE _rs :

Travel demand between an OD pair (r, s) at user equilibrium

d ^max _rs :

Maximum travel demand between an OD pair (r, s)

κ _rs :

Generalized cost of travel between an OD pair (r, s)

Ψ :

Generalized cost sensitivity of demand

A :

Set of all the links in the network

M :

Number of nodes in the network

x ^UE _ij :

Flow on link (i, j) at user equilibrium

$\varvec{x}^{{\varvec{SO}}}$ :

Link flow vector at system optimal

t _ij :

Travel time on link (i, j)

$\varvec{t}^{{\varvec{SO}}}$ :

Link travel time vector at system optimal

$\varvec{\tau}_{{\varvec{FB}}}$ :

First-best toll vector

$\varvec{\pi}^{rs}$ :

Vector of total travel costs from origin r to all nodes

$\varvec{A}$ :

Node-link incidence matrix for the network

$\varvec{E}^{rs}$ :

Column vector of length M for an OD pair (r, s), with +1 and −1 at position r and s, and 0 elsewhere

θ :

Planner-assigned weight to the expected value of system performance

$\Phi$ :

Objective function

The proposed framework in this study is presented in a sequence of components as follows:

• Developing a method for incorporating stochasticity in formulations of elastic demand functions

• Quantifying appropriate system performance metrics for evaluation purposes

• Estimating first-best tolls for elastic demand scenarios

• Defining an objective function

• Developing the method to find the nearest optimal toll vector for the combined S-ED scenario

The following subsections describe each of them.

Stochastic-elastic demand function formulation

The parameters of demand functions involve forecasts related to land use, trip generation, demographics, and adoption rates of new technologies. (For instance, these affect the number of residents in a zone, their value of time, and so forth.) These forecasts also involve sampling error in estimating parameters from surveys or other observations of travel behavior. Our use of stochastic elastic demand functions is meant to represent the uncertainty in these forecasts, which then translates to uncertain parameters in the demand functions. The correct distribution of these parameters in the demand function, and how uncertainty in forecasts translates into error in demand functions, is complicated and depends greatly on the specific travel demand models used. Thus instead of deriving expressions for such distributions for different travel demand models, we show how the resulting uncertainty can interact with demand elasticity in the context of toll-setting.

The stochastic elastic demand function (called S-ED function henceforth for brevity) aims at accounting for the dependence and responsiveness of demand to active network conditions, and simultaneously incorporates uncertainties in the demand. The demand function is formulated here as a linear or exponential function, as appearing in Eqs. 1, 2, and 3. Under an inelastic demand scenario, first-best congestion pricing methodologies that aim to incorporate demand uncertainty assume the actual demand value as a random variable (Gardner et al. 2008). In the case of elastic demand, different parameters in the demand function can be made stochastic. Typical elastic demand functions include some maximum demand value for each OD pair d ^max _rs along with shape parameters indicating the sensitivity of demand to congestion levels. The authors believe that the maximum demand d ^max _rs is better modeled as stochastic (i.e., as a random variable with pre-specified probability distributions) than these latter parameters, because long-range forecasting errors involving land use and economic growth (which affect $d_{rs}^{max}$)are likely larger than those involving values of time and travel (which affect the other parameters). The value of time is assumed to be homogeneous, and units are chosen so that the value of time is unity. Examples of demand functions which are tested in this paper include:

$$D_{rs} = d_{rs}^{max} - \varPsi \kappa_{rs} ,\quad \forall \left( {r,s} \right) \in Z^{2} \,\left( {Linear \, Relationship} \right)$$

(1)

$$D_{rs} = d_{rs}^{max} e^{{\frac{{ - \varPsi \kappa_{rs} }}{{d_{rs}^{max} }}}} ,\quad \forall \left( {r,s} \right) \in Z^{2} \,\left( {Exponential \, Relationship} \right)$$

(2)

with the actual demand in either case given by:

$$d_{rs} = \left\{ {\begin{array}{*{20}c} {D_{rs} } & {for\; D_{rs} \ge 0} \\ {0 } & {for\;D_{rs} < 0} \\ \end{array} } \right.$$

(3)

Mathematical properties of the S-ED function in Eqs. (1) and (2) are highlighted here. The S-ED function is decreasing in κ _rs and is invertible. The invertible nature is convenient in quantifying relevant system performance metrics, as shown in the next subsection. The generalized cost sensitivity of demand, Ψ is assumed to be the same for all OD pairs.

System performance metric–traveler surplus (TS)

Under inelastic demand assumptions, TSTT is a common metric used to quantify the system performance (Gardner et al. 2008; Waller et al. 2001). However, under the elastic demand framework, the number of travelers is endogenous and it does not make sense to simply minimize total travel cost (since that could trivially be accomplished by setting all tolls to large amounts by eliminating travel altogether). Hence, under the elastic demand scenario, TS, is used as the system performance metric (Eq. 4). It represents the total difference between travelers’ willingness-to-pay and the actual travel times experienced:

$$TS = \mathop \sum \limits_{{\left({r,s} \right) \in Z^{2}}} \int\nolimits_{0}^{{d_{rs}^{UE}}} {D_{rs}^{- 1} \left(\omega \right)d\omega - \mathop \sum \limits_{{\left({i,j} \right) \in A}} t_{ij} \left({x_{ij}^{UE}} \right)x_{ij}^{UE}}$$

(4)

The first term in Eq. 4 represents the aggregated amount of time that users traveling at user equilibrium are willing to spend. The link flows (x ^UE _ij ) are obtained by solving deterministic user equilibrium (UE) with the elastic demand to find the second term (Gartner 1980). It represents the actual aggregated amount of travel time experienced by all users in the system (TSTT) at UE. The difference between them thus gives the system-wide aggregated travel time surplus. For every OD pair in the network, the inverse demand function D ⁻¹ _rs (ω) is dependent on the maximum demand d ^max _rs which is modeled as a random variable (see “Stochastic-elastic demand function formulation” section); TS is thus a random variable.

Minimum revenue first-best pricing under elastic demand

Since the objective of implementing tolls in this study is overall improvements in system performance and not revenue generation, the minimum revenue (MR) pricing model is applied in this scenario. As compared to marginal cost pricing, MR tolls are more stable in case of varying demands and also more economically equitable owing to lesser total system revenue and lesser out-of-pocket costs. They are also ‘less confusing’ to users, as marginal cost based tolls need to be varied with time as congestion varies (see Penchina 2003).

Finding a system optimal (SO) solution is the first step while solving first-best MR pricing problems. The SO problem maximizes the net benefit of users in the form of traveler surplus. Incorporation of elasticity in the demand does not change the approach of solving SO problems and it can be solved as a “user equilibrium (UE) problem with elastic demand” after the addition of marginal social costs $\left( {x_{ij} \frac{{dt_{ij} }}{{dx_{ij} }}} \right)$ in the link-performance function of all links (Yang and Huang 1998). After solving the SO problem, first-best tolls are found in the case of elastic demand by solving the following linear program (LP) first formulated by Yildirim and Hearn (2005).

$$\mathop {\hbox{min} }\limits_{{\varvec{\tau}_{{\varvec{FB},\varvec{\pi}}} }} \left( {\varvec{\tau}_{{\varvec{FB}}} } \right)^{T} \varvec{x}^{{\varvec{SO}}}$$

subject to:

$$\varvec{t}^{{\varvec{SO}}} + \varvec{ \tau }_{{\varvec{FB}}} \ge \varvec{ }\left( \varvec{A} \right)^{\varvec{T}}\varvec{\pi}^{rs} ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

$$D_{rs,SO}^{ - 1} \le \left( {\varvec{E}^{rs} } \right)^{T}\varvec{\pi}^{rs} ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

$$\left( {\varvec{t}^{{\varvec{SO}}} + \varvec{ \tau }_{{\varvec{FB}}} } \right)^{T} \varvec{x}^{{\varvec{SO}}} = \left( {\varvec{D}_{{\varvec{SO}}}^{ - 1} } \right)^{\varvec{T}} {\mathbf{d}}^{{\varvec{SO}}}$$

Objective function under S-ED scenario

The vector of optimal S-ED functions is defined as the one that gives the tolls vector $\varvec{\tau}_{{\varvec{FB}}}$, for which TS attains the maximum expected value, and at the same time the minimum standard deviation. Under practical scenarios, however, both objectives of maximizing the expected value of TS and minimizing its standard deviation may not be achievable simultaneously. Hence, planners or policy-makers may assign relative weights to each of these components according to their inherent responsiveness to risk and the objectives as per the system characteristics. Thus, the objective function ($\Phi$) can be represented as follows:

$$\Phi \left( {{\mathbf{d}}^{{{\mathbf{max}}}} } \right) = \theta E\left[ {TS\left( {\varvec{\tau}_{{\varvec{FB}}} \left( {{\mathbf{d}}^{{{\mathbf{max}}}} } \right)} \right)\left] { - \left( {1 - \theta } \right)\sigma } \right[TS\left( {\varvec{\tau}_{{\varvec{FB}}} \left( {{\mathbf{d}}^{{{\mathbf{max}}}} } \right)} \right)} \right]$$

(5)

In the pricing decision under the S-ED scenario, the objective is to find a vector ${\mathbf{d}}^{{{\mathbf{max}}}}$ (and corresponding toll vector $\varvec{\tau}_{{\varvec{FB}}}$ ) that maximizes $\Phi$ for a given value of weight θ. The value of θ reflects the relative importance or weight given to the expected value of TS, relative to its standard deviation.

Optimal toll vector under the S-ED scenario

Gardner et al. (2008) formulated the first-best congestion pricing problem, under the S-ID scenario, as a stochastic mathematical program on a non-convex feasible region. Exact non-linear programming methods are intractable for these complex optimization problems and, therefore, they proposed approximate methods. The inclusion of elasticity along with the uncertainty of demand makes this problem even more intractable. Therefore, this study proposes a method to find the nearest optimal tolls under the S-ED scenario, integrating the different elements of the framework developed in the preceding subsections.

As mentioned earlier, at the time of pricing decisions, planners know the probability distribution of the future maximum demand of each OD pair in the network. For a general network having k OD pairs, the future maximum demand vector would thus be a joint probability distribution of these k marginal demand distributions. For instance, for a small network with a single OD pair with a discrete distribution of future maximum demand (ranging from, say 0–100), planners can enumerate all possible values. However, it is not possible to realize all future maximum demand vectors for continuous demand distributions and larger networks used in practical applications. Therefore, in this framework, a finite number of realizations (n) of the maximum demand vector, from both right and left tails around its mean, are first considered. For each realization of maximum demand, the first-best toll vector is calculated. Subsequently, each toll vector is applied to the network and objective function (for pre-specified $\theta$) is evaluated by solving UE for another set of (say r) realizations of maximum demand vector (sampled from probability distribution of maximum demand). The value of r can be chosen to attain a sufficiently narrow 95% confidence interval of the expected value of TS.

Gilman (1968) suggested a straightforward stopping rule for independent samples in Monte Carlo simulations so that the expected value of TS is estimated by a confidence interval of length d and convergence probability greater than α: $E\left( r \right) = \frac{{Z_{\alpha }^{2} S^{2} }}{{d^{2} }}$, where S ² is a sample variance and Z is a standard normal random variable $\left( {Z_{\alpha } = 1.96 for \alpha = 0.95} \right)$. So, the narrower the length of the 95% confidence interval (i.e., d), the higher the number of samples (i.e., r) required. However, some studies use empirical observations to determine the stopping criteria; for instance Waller et al. (2001) terminate Monte Carlo sampling at a sample size of around 2000 when sample mean appears to be sufficiently stable with increase in sample size.

The toll vector corresponding to the maximum value of the objective function is the optimal solution for this framework. Although this framework does not guarantee a global optimal toll vector, but provides a plausible pricing policy. Choices of r and n, for both a small and a relatively large network, are shown in the subsequent “Model framework demonstration I: Braess network, Model framework demonstration II: Friedrichshain Center, Berlin study area and Robust pricing experiment: Sioux Falls study area” sections. The proposed heuristic is as follows:

• Step 1 Set i = 0: First realization of the future maximum demand vector (or maximum planning demand vector)

• Step 2 Solve the SO problem with this future maximum demand vector and estimate first-best tolls ($\varvec{\tau}_{{\varvec{FB}}}$ ) by solving the LP.

• Step 3 Apply the calculated link tolls (obtained from Step 2) and solve the UE traffic assignment problem for r realizations of the future maximum demand vectors

• Step 4 For the assigned weight θ, calculate the value of objective function $\Phi$ (from Eq. 5) by computing expected value and standard deviation of TS.

• Step 5 Set i = i + 1 : Next realization of the future maximum demand vector

• Step 6 If i < n, go to Step 2. Else go to Step 7

• Step 7 Choose the toll vector ($\varvec{\tau}_{{\varvec{FB}}}$) corresponding to the vector of S-ED functions giving the maximum value of $\Phi$.

Model framework demonstration I: Braess network

In this section, congestion pricing frameworks in two elastic demand scenarios (stochastic, S-ED and deterministic, D-ED) are demonstrated on a small transportation network with a single OD pair as shown in Table 1. The demonstration network is the well-known Braess network. The effects of introducing stochasticity in the elastic demand function, and subsequent pricing decisions are investigated. This small network is studied as a first demonstration, and the following sections apply the same framework in the more realistic settings.

Table 1 Specifications of the test network for demonstration

Model formulations for S-ED and D-ED scenarios

The network parameters are shown in Table 1. The network has only one OD pair (node 1 to node 4), and the following elastic demand function, along the lines of Eq. 1 (where d ^max₁₄ is a random variable):

$$D_{14} = d_{14}^{max} - \varPsi \kappa_{14} ,\quad \forall d_{14}^{max} \in \left[ {20,80} \right]$$

(6)

It is assumed under the S-ED scenario that d ^max₁₄ has a discrete uniform probability distribution with an expected value of E[d ^max₁₄ ] = 50, with values ranging from 20 to 80 at an interval 1. This represents the possibilities of the future maximum demand being subject to uncertainties and having not just a single value, but a range of possible realizations. However, if a planner intends to set the tolls according to the demand function with the expected value of the maximum demand (E[d ^max₁₄ ]), it gives rise to the deterministic scenario (D-ED). The corresponding elastic demand function is presented in Eq. (7).

$$D_{14}^{det} = E\left[ {d_{14}^{max} } \right] - \varPsi \kappa_{14} = 50 - \varPsi \kappa_{14}$$

(7)

In the D-ED scenario, tolls can be set by the planner for system optimization corresponding to only the obtained elastic demand function in 4. On the other hand, in the S-ED framework, the motive is to find the optimal S-ED function that gives the toll vector $\left( {\varvec{\tau}_{{\varvec{FB}}} } \right)$ which maximizes the objective function defined in the Eq. 5 for weights assigned by the planner.

Method

The earlier developed generalized congestion pricing heuristic for the S-ED scenario is demonstrated in this application. The initial maximum demand value i is 20 in this case (see Step 1). Since this is a smaller test network with just one OD pair and discrete distribution of maximum demand, as mentioned earlier, all possible demand realizations from 20 to 80 (i.e., n = r = 61, see Steps 3 and 6 of the method in “Optimal toll vector under the S-ED scenario” section) can be enumerated. The possibility of full enumeration of all demand realizations in the Braess network also provides an opportunity to obtain an exact solution (“S-ED Exact” in Fig. 1) and compare it with the heuristic’s solution.

Fig. 1

Braess network results for system performance and optimal elastic demand functions under the S-ED and D-ED frameworks

To obtain the heuristic solution (“S-ED Heuristic” in Fig. 1), tolls are calculated for $d^{max} = \left\{ {20, 30, 40, 50, 60, 70, 80} \right\}$ in Step 2, implying i = 20 in Step 1, and n = 7 in Step 6 of the heuristic. Moreover, r = 61 is considered in Step 3 of heuristic to avoid the need for Monte-Carlo sampling.

Results and analysis

The above method is applied for a generalized cost sensitivity of Ψ = 1. Test results are shown in Fig. 1, which displays the expected values and standard deviations of TS under D-ED and S-ED scenarios (calculated in Step 4 of the method in “Optimal toll vector under the S-ED scenario” section) in (a) and (b), respectively. Additionally, the optimal forecasted demand in Fig. 1c is the maximum demand value in elastic demand functions corresponding to the optimal toll vectors $\varvec{\tau}_{{\varvec{FB}}}$ that maximize $\Phi$ for different values of weights assigned by planners.

Equivalence of results in S-ED and D-ED scenarios

Under the D-ED scenario, the optimal elastic demand function is D ^det₁₄ (see Eq. 10). Planners would then set tolls based only on this obtained D-ED function. However, it would not be so under the S-ED scenarios having stochastic component (d ^max₁₄ ) in the elastic demand functions.

A comparison is drawn between the D-ED and the S-ED (Exact and Heuristic) scenarios based on the optimal demand function outcomes corresponding to different weights (θ). These weights are a prerogative of planners or policymakers which are assigned based on system performance objectives and risk-taking ability. It can be inferred from Fig. 1c that when planners propose a weight 0.7 ≤ θ ≤ 1.0, the optimal elastic demand functions (and thus the optimal toll vector $\varvec{\tau}_{{\varvec{FB}}}$) for the S-ED scenarios correspond closely to one for the D-ED scenario. The optimal toll vector remains constant across a range of planning decisions that can be made by planners using these weights. It can be inferred that the pricing decisions under the S-ED scenarios are fairly stable in terms of different policy objectives. This stability addresses a different set of planning challenges, where there might be uncertainties associated with planners’ decision-making process in terms of achieving the trade-off between system performance (E[TS]) and robustness (σ[TS]). The correspondence between the optimal pricing decisions under the S-ED and D-ED scenarios also indicates that incorporation of the elasticity feature in demand offsets the need of accounting for its uncertainty.

Characterization of weights

As mentioned earlier, the elastic demand function for which the expected system performance is visibly the best might not be so in terms of robustness, and vice versa. This is also evident from the plots in Fig. 1a, b for E[TS] and σ[TS] against the maximum planning demand. It is seen that the S-ED function corresponding to maximum E[TS] is D ₁₄ = 52 − κ ₁₄, whereas the one corresponding to minimum σ[TS] is D ₁₄ = 20 − κ ₁₄. Therefore, weights can be set by planners for improving system performance and robustness, depending on the system objectives to be attained and also characteristics of the system.

Decision-makers are likely to lay higher stress on the system performance in most practical cases using higher weights. This is the case of inefficient systems that require significant performance improvements and are not expected to undergo any significant demographic and land use shifts in the long-term. Lower weights, on the other hand, represent higher importance to the deviation from this expected performance, evoking elements of inherent risk-aversion characteristics in long-term planning decisions. From the transportation planning standpoint, such behavior is apposite when the system is very susceptible to experience variations in demand and built environment.

Near optimality of the heuristic

When possible, it is important to compare the performance of any heuristic with the exact optimal solution and thus a similar comparison is performed here. Figure 1a shows that maximum E[TS] occurs at the tolls corresponding to maximum planning demand of 52 and 50 in S-ED exact and S-ED heuristic scenarios, respectively, which are close to each other. Furthermore, subplot (c) indicates that for the range (0.5–1.0) of weights assigned by the planner, the optimal forecasted demand in both scenarios is very close. Thus for this numerical experiment, the heuristic-based solution is close to the exact optimal solution.

The proposed heuristic to calculate tolls under S-ED scenario considers a finite number of realizations (n) of the maximum demand vector (in Step 2), from both left and right tails around its mean. If sufficient number of maximum demand vector realizations (r) is sampled in Step 3 of heuristic, then n serves as the limiting factor here, i.e., higher the value of n, heuristic solution is likely to be closer to the exact optimal solution. If both n and r equal to all possible realizations of maximum demand (which is practically unfeasible for a larger network with continuous probability distribution of maximum demand vector), it is obvious that the heuristic’s solution will hit the exact optimal solution.

Model framework demonstration II: Friedrichshain Center, Berlin study area

The proposed heuristic is now extended to a larger study area. The Friedrichshain Center network of Berlin, Germany is chosen, which contains 224 zones, 523 links, and 506 OD pairs. The data for this network are obtained from Bar-Gera (2010).

Model formulations for S-ED and D-ED scenarios

In this case, the maximum demand between every OD pair is assumed to be a uniformly distributed random variable, with a linear elastic demand function (see Eqs. 8, 9). For observable effects of the elastic nature, a generalized cost sensitivity of Ψ = 0.1 is used in this application, based on the relative magnitudes of the demand and generalized costs between OD pairs.

$$D_{rs} = d_{rs}^{f} - 10\kappa_{rs} ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

(8)

$$d_{rs}^{max} \sim{\mathcal{U}}\left( {0.5d_{rs}^{f} ,1.5d_{rs}^{f} } \right) ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

(9)

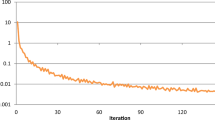
For finding optimal tolls in the S-ED scenario, the demonstration in “Model framework demonstration I: Braess network” section used a network small enough to allow enumeration of all possible demand scenarios for the single OD pair. This strategy is impractical on the Berlin network. The expected value of the maximum demand vector is the forecasted demand vector ${\mathbf{d}}^{{\mathbf{f}}}$, and tolls are calculated (in Step 2 of the method in “Optimal toll vector under the S-ED scenario” section) at ${\mathbf{d}}^{{\mathbf{f}}}$ and ten additional realizations, five higher and five lower. These include $\left\{ {0.5{\mathbf{d}}^{{\mathbf{f}}} , 0.6{\mathbf{d}}^{{\mathbf{f}}} , \ldots ,1.4{\mathbf{d}}^{{\mathbf{f}}} , 1.5{\mathbf{d}}^{{\mathbf{f}}} } \right\}$, thus implying an initialization of $i = 0.5{\mathbf{d}}^{{\mathbf{f}}}$ in Step 1 and n = 11 in Step 6. Under this application, the LP containing 12,581 inequality constraints and 5676 variables is solved to find the SO solution in Step 2 of the heuristic. Further, Monte Carlo sampling is used in Step 3 to generate demand scenarios according to the probability distribution of the maximum demand vector. This is observable in Fig. 2 where the expected value of the TS does not fluctuate much beyond a thousand samples, thus r = 1000 is considered in Step 3. An analytical method (Gilman 1968) is used to check the accuracy of this empirical method by tracing back the length of the 95% confidence interval. This length $\left( {\sqrt {\frac{{1.96^{2} S^{2} }}{1000}} } \right)$ is reasonably narrow (0.38% of the sample mean of TS) with 1000 samples, implying that $r = 1000$ is a sufficient stopping criteria for this case.

Fig. 2

System performance variation under Monte-Carlo sampling

Results and analysis

System performance along with the corresponding optimal demand realizations are obtained post-application. Figure 3 displays the expected values and standard deviations of TS (calculated in Step 4 of the method in “Optimal toll vector under the S-ED scenario” section) and optimal proportions of the forecasted demand vector under D-ED and S-ED scenarios in subplots (a), (b), and (c), respectively.

Fig. 3

Friedrichshain Center network results for system performance and optimal planning demand

The comparison under the D-ED and S-ED scenarios is drawn based on the optimal demand function outcomes corresponding to different weights (θ). Figure 3c shows the equivalence of the optimal elastic demand functions (or optimal proportions of the forecasted demand) under a wide range of planning objectives and risk preferences represented by the weights. In other words, when planners assign weights ranging from 0.3 ≤ θ ≤ 1.0, the optimal elastic demand functions (and thus the optimal toll vector $\varvec{\tau}_{{\varvec{FB}}}$) for the S-ED scenarios correspond to the D-ED scenario. These observations show that pricing decisions under the S-ED scenarios are fairly stable under different planning objectives. Consistent with the hypothesis (see “Motivation and theoretical basis” section), the equivalence between the optimal pricing decisions under the S-ED and D-ED scenarios conveys that inclusion of demand elasticity in the pricing decisions can exhibit a restoring effect against inherent demand uncertainties, as also was seen in the Braess network demonstration.

Robust pricing experiment: Sioux Falls study area

In this third numerical experiment, apart from the S-ED and D-ED scenarios, S-ID and D-ID scenarios are also implemented, which are more commonly used in practice. This is with the intent to relatively evaluate all possible demand scenarios and investigate the different optimal pricing decision outcomes under each of them. The Sioux Falls, SD area network is chosen, which contains 24 nodes, 76 links, and 552 OD pairs. The data for this network are also obtained from Bar-Gera (2010). The distribution of the forecasted demand vector (through standard travel demand forecasting paradigms used by planners) is assumed to be the same across all the four cases for evaluation purposes. However, its realization varies across the scenarios. In the elastic scenario, it is used as the maximum demand vector while, in the inelastic framework, it corresponds to the actual demand vector.

Model formulations for S-ED and D-ED scenarios

In this case, for the S-ED model, the maximum demand between every OD pair is assumed to be a random variable following a continuous uniform and normal probability distribution. As discussed earlier, the elastic demand function is formulated as a linear or exponential function. For observable effects of the elastic nature, a generalized cost sensitivity of Ψ = 10 is used in this application, based on the relative magnitudes of the demand and generalized costs between OD pairs. Table 2 represents the four elastic demand functions developed for this application:

Table 2 Possible combinations of elastic demand functions

The equivalent deterministic case (D-ED) occurs at the expected value of the maximum demand (forecasted), and can be represented as follows:

$$D_{rs} = d_{rs}^{f} - 10\kappa_{rs} ,\quad \forall \left( {r,s} \right) \in Z^{2} \,\left( {Linear \, Relationship} \right)$$

(10)

$$D_{rs} = d_{rs}^{f} e^{{\left( {\frac{{ - 10\kappa_{rs} }}{{d_{rs}^{f} }}} \right)}} ,\quad \forall \left( {r,s} \right) \in Z^{2} \,\left( {Exponential \, Relationship} \right)$$

(11)

The expected value of the maximum demand vector is the forecasted demand vector ${\mathbf{d}}^{{\mathbf{f}}}$, and tolls are calculated (in Step 2 of the method in “Optimal toll vector under the S-ED scenario” section) at ${\mathbf{d}}^{{\mathbf{f}}}$ and ten additional realizations, five higher and five lower. These include $\left\{ {0.5{\mathbf{d}}^{{\mathbf{f}}} , 0.6{\mathbf{d}}^{{\mathbf{f}}} , \ldots ,1.4{\mathbf{d}}^{{\mathbf{f}}} , 1.5{\mathbf{d}}^{{\mathbf{f}}} } \right\}$, thus implying an initialization of $i = 0.5{\mathbf{d}}^{{\mathbf{f}}}$ in Step 1 and n = 11 in Step 6. Under this application, the LP containing 2352 inequality constraints and 652 variables is solved to find the SO solution in Step 2 of the heuristic. Further, Monte Carlo sampling is used in Step 3 to generate demand scenarios according to the probability distribution of the maximum demand vector. Figure 4 indicates that the expected value of the TS does not fluctuate much beyond a thousand samples, thus r = 1000 is considered in Step 3. As in the previous demonstration, the analytical method by Gilman (1968) is used to check the accuracy of this empirical method by tracing back the length of the 95% confidence interval. This length $\left( {\sqrt {\frac{{1.96^{2} S^{2} }}{1000}} } \right)$ is again reasonably narrow (0.43% of the sample mean of TS) with 1000 samples, implying that $r = 1000$ is a sufficient stopping criterion for this case.

Fig. 4

System performance variation under Monte-Carlo sampling

Model formulations for S-ID and D-ID scenarios

The traditional traffic assignment problem assumes inelastic demand. Under the S-ID scenario, the element of uncertainty is introduced only in the actual demand between the OD pairs in the network. In consonance with the probability distributions of maximum demand (d ^max _rs ) in the S-ED scenario, S-ID considers the actual demand to be a random variable with uniform and normal probability distributions, having actual forecasted demand $\left( {d_{rs}^{f} } \right)$ as the expected value. A detailed methodology to find nearest optimal tolls under S-ID scenario can be found in Gardner et al. (2008).

$$d_{rs} \sim{\mathcal{U}}\left( {0.5d_{rs}^{f} ,1.5d_{rs}^{f} } \right) ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

(12)

$$d_{rs} \sim{\mathcal{N}}\left( {d_{rs}^{f} ,\left( {\frac{1}{6}d_{rs}^{f} } \right)^{2} } \right) ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

(13)

The corresponding deterministic case, D-ID will occur when the system is evaluated at only the expected value of the forecasted demand, represented as follows:

$$d_{rs} = d_{rs}^{f} ,\quad \forall \left( {r,s} \right) \in Z^{2}$$

(14)

System objectives

Under an inelastic scenario, a dual-objective optimization approach of improving the TS and reducing the standard deviation in it cannot be realized. This is because there is no notion of a travel time surplus due to the inherent fixities in demand. In this case, the system performance measure thus becomes TSTT, the aggregated sum of the travel time of all users in the network. In this case, the objective of simultaneously minimizing the expected value of TSTT and its standard deviation is followed. It is represented as:

$$\Phi \left( {\mathbf{D}} \right) = \theta E\left[ {TSTT\left( {\varvec{\tau}_{{\varvec{FB}}} \left( {\mathbf{D}} \right)} \right)\left] { - \left( {1 - \theta } \right)\sigma } \right[TSTT\left( {\varvec{\tau}_{{\varvec{FB}}} \left( {\mathbf{D}} \right)} \right)} \right]$$

(15)

Results and interpretation

The results obtained under all demand scenarios for system performance and optimal decision-making to satisfy planner objectives are shown in Figs. 5 and 6. They show results corresponding to uniform and normal distribution scenarios respectively.

Fig. 5

Sioux Falls network results for system performance and optimal planning demand—uniform distribution case

Fig. 6

Sioux Falls network results for system performance and optimal planning demand—normal distribution case

In Figs. 5 and 6, subplots (a) through (f) show the performance metrics under the various demand relationships considered (linear elastic, exponential elastic, and inelastic). Subsequently, subplots (g) through (i) show the maximum demand (as a fraction of ${\mathbf{d}}^{{\mathbf{f}}}$) in elastic demand (S-ED and D-ED) scenarios (or actual demand in case of S-ID and D-ID scenarios) corresponding to the optimal toll vectors that maximize the $\Phi$ for different values of weights assigned by planners.

System performance metrics

Comparing subplots (a) and (c), with (e) in Figs. 5 and 6 reveal the opposite nature of the expected value plots (in terms of convexity) in elastic and inelastic cases. This is attributed to the fact that system performance measures are different in both the cases, TS in the former and TSTT in the latter.

In the S-ED scenario, the maximum expected TS is obtained at the elastic demand functions corresponding to the expected value of maximum demand (${\mathbf{d}}^{{\mathbf{f}}} )$. For the S-ID scenario, it is observed from Figs. 5e and 6e that the minimum expected value of TSTT occurs at an actual demand value of $0.9{\mathbf{d}}^{{\mathbf{f}}}$. However, the standard deviations of TS and TSTT at these values are not minimum. Thus, planners might want to choose other demand values that provide a lesser standard deviation, in accordance with their system objectives (according to their risk responsiveness) and characteristics.

Demand model outcomes and planner objectives

The optimal elastic demand functions in the S-ED scenario seen from subplots (g) and (h) in Figs. 5 and 6 give policy insights related to the robustness (in terms of planners’ objectives) of pricing decisions under elastic demand scenario. It is seen that depending on the importance planners might attach to system performance through weights, different optimal vectors of elastic demand functions are obtained. Under the S-ED framework, the optimal demand vector remains constant for most part of the range of possible weights (θ ≥ 0.2) that can be assigned by planners. Moreover, the decisions to be made under the D-ED and S-ED scenarios coincide. This implies that when the toll vector $\varvec{\tau}_{{\varvec{FB}}}$ obtained under the S-ED scenario corresponding to θ ≥ 0.2 is applied onto the network, it corresponds to the $\varvec{\tau}_{{\varvec{FB}}}$ applied based on the D-ED scenario. Additionally, this correspondence between pricing decisions under the S-ED and D-ED scenarios is consistent across combinations of demand distributions (uniform and normal) and elastic demand relationships (linear and exponential); and thus, findings support the hypothesis stated in “Motivation and theoretical basis” section.

These findings further bolster the stability of pricing decisions under the S-ED scenario. It can be pointed here that similar robustness aspects were gleaned from the test network demonstration (see “Equivalence of results in S-ED and D-ED scenarios” section). On the other hand, such a correspondence is not observed between the S-ID and D-ID scenarios as seen from Figs. 5i and 6i, indicating the advantages obtained through accounting for the elastic nature of demand. At the same time, the proposed approach to incorporate this elastic nature of demand along with uncertainty by formulating random variable-based elastic demand functions are designed to be tractable and transparent. This is with the purpose of making the framework easily understandable to planners, and also for ease of integration with existing regional transportation planning models.

Qualitatively, as inferred from the previous two applications, it can be again upheld that consideration of the elastic nature of demand is seen to offer a form of ‘restoring mechanism’ to the uncertainties manifesting in forecasted demand. From the practitioner standpoint, the incorporation of elastic demand thus mitigates the impacts of being unable to account for uncertainties associated with demand.

The optimal toll values obtained for the current Sioux Falls application under different demand scenarios are presented in Table 3.

Table 3 Optimal toll values for the Sioux Falls application

Conclusions and future work

The paper investigates the hypothesis that demand elasticity can offset the effects of demand uncertainty on the system perforamce and optimal first-best tolls under the deterministic-elastic and stochastic-elastic demand scenarios coincide. It is proven that this is true under the assumptions of linear cost and demand functions, and fixed path set. The hypothesis is further investigated numerically on networks with nonlinear functions and a variable equilibrium path set.

To this end, this study proposes a heuristic to find approximately optimal tolls considering the stochasticity and elasticity of future demand (S-ED scenario). Additionally, a system optimization objective function accounting for the planners’ dual interests of maximizing the system performance (TS in this study) and minimizing deviation from predicted performance is considered. Planners might want to employ different weights based on the system characteristics, its current state, and the desired future performance. Two numerical experiments are carried out for the purpose of method demonstration on the small-scale Braess network and relatively larger Friedrichshain Center, Berlin study area. The results suggest that optimal pricing decisions under S-ED and D-ED scenarios coincide for a broad range of weights assigned by the planners.

Further, pricing decisions in deterministic-elastic (D-ED) and inelastic demand scenarios (S-ID and D-ID) under plausible planner objectives are also obtained to investigate the implications of each in the absolute and relative sense. A third numerical experiment on the Sioux Falls study area is performed for this comparison. It is consistently noted from all the above applications that when planners explicitly incorporate elastic demand in the modeling process, it appears to provide a counter-action against the effects of uncertainties associated with forecasted demand, under the current set of assumptions and functional forms.

Several future research avenues emerge based on the current study. This study assumes that distribution of future maximum demand and the elastic relationship of actual demand are known to the planners, which may or may not be true in practical applications. Furthermore, the distribution of the parameters of demand function and how uncertainty in forecasts translates into error in demand functions depends on the specific travel demand models used. Therefore, there is a need to investigate the sensitivity of the results by incorporating more combinations of the probability distributions of future maximum demand and elastic demand relationships. Additionally, second-best congestion pricing strategies under the S-ED scenario open the door to a wide array of theoretical and practical research problems.

Appendix

The results in this “Appendix” do not depend on the number of links, nodes, or OD pairs in a network, but only on linearity of the cost and demand functions, and conditions which intuitively express that the set of used paths does not change with the demand realization. The general result is followed by an illustrative example. The theorem below requires several restrictive assumptions, motivating the numerical analyses in the main text on large-scale networks which do not satisfy these conditions.

Let $\Xi$ denote the support of the random vector $\epsilon$, and T the set of feasible toll vectors. We will divide the space $\Xi \times T$ into subsets $\Pi_{i}$ according to the sets of minimum-cost paths at the user equilibrium solutions, depending on the demand realization and applied tolls. Formally, there exist a finite number of disjoint open sets $\Pi_{1} ,\Pi_{2} , \ldots \Pi_{P}$, all subsets of $\Xi \times T$, which satisfy the following properties:

• 1. For any $\left({\epsilon, \tau} \right) \in {\Pi}_{i}$, when the demand is given by $d + \epsilon$ and the toll vector is τ, the set of minimum-cost paths connecting all OD pairs at the user equilibrium solution is the same for all such pairs in the same set $\Pi_{i}$.

• 2. For each set $\Pi_{i} ,$ and for each $\left({\epsilon, \tau} \right) \in {\Pi}_{i}$, there exists at least one equilibrium path flow solution with strictly positive flow on all minimum-cost paths when demand is $d + \epsilon$ and tolls are τ.

• 3. The union of the closure of the sets $\Pi_{i}$ is the entire space $\Xi \times T$.

We now show that, among toll vectors $\hat{\tau }$ for which the set of used paths is the same regardless of the realization $\epsilon$, the tolls maximizing expected surplus with respect to $\epsilon$ also maximize the surplus when $\epsilon = 0$ deterministically when the cost and demand functions are linear and $\epsilon$ has zero mean. The first condition can be expressed as restricting the toll vectors under consideration to those $\tau$ such that $\Xi \times \left\{ \tau \right\} \subseteq {\text{cl}} \Pi_{i}$ for some set $\Pi_{i}$.

Theorem

Consider a network with any number of nodes, links, and OD pairs satisfying the following conditions:

• 1. The travel time on each link takes the form $t_{ij} \left( {x_{ij} } \right) = L_{ij} + M_{ij} x_{ij}$ where M _ij  > 0.

• 2. The inverse demand function for OD pair (r, s) is of the form $D_{rs}^{- 1} \left({d_{rs}} \right) = C_{rs} + \epsilon_{rs} - F_{rs} d_{rs}$ where F _rs  > 0.

• 3. The set of feasible tolls T has the property that $\Xi \times T \subseteq {\text{cl}} \Pi_{i}$ for some set $\Pi_{i}$.

• 4. For each OD pair (r, s), $E\left[{\epsilon_{rs}} \right] = 0$.

In such a network, a toll vector maximizes traveler surplus when $\epsilon = 0$ (the “deterministic case”) if and only if it maximizes expected traveler surplus when $\epsilon$ has any distribution satisfying conditions 1 and 2.

Proof

For any realization $\epsilon$, equilibrium link flows and OD demands exist and are unique, so functions $x(\epsilon)$ and $d(\epsilon)$ giving these values in terms of $\epsilon$ are well-defined, and the domain of these functions is the support of $\epsilon$. (Patriksson 1994). Furthermore, Condition 2 and the properties of $\Pi_{i}$ discussed above imply that the equilibrium solutions $x(\epsilon)$ are strictly complementary for all $\epsilon$ except possibly at the boundary (that is, there exists a corresponding path flow solution in which all minimum-cost paths have positive flow), so the functions $x(\epsilon)$ and $d(\epsilon)$ are differentiable on $\Pi_{i}$ (Proposition 2.2 and Theorem 2.3 of Lu 2008). Furthermore, these derivatives correspond to the solution of “linearized” elastic demand equilibrium problems (Patriksson 2004; Josefsson and Patriksson 2007; Lu 2008). Under Conditions 1, 2, and 3, these derivatives are identical for all realizations of $\epsilon$, the sensitivity analysis is exact, and these functions are linear in $\epsilon$. That is, we can express $x(\epsilon)$ and $d(\epsilon)$ in the forms

$$x_{ij} \left(\epsilon\right) = J_{ij} + \epsilon \cdot K$$

$$d_{rs} \left(\epsilon\right) = A_{rs} + \epsilon \cdot B$$

where K and B are constant vectors of the same dimension as $\epsilon$, and J _ij and A _rs are link- and OD-specific constants, respectively. Furthermore, of these constants, only the A _rs and J _ij directly depend on the specific toll vector τ; by linearity, the constants B and K depend only on the set of $\Pi_{i}$ which is independent of τ by Condition 3.

The total system travel time is thus a quadratic function of $\epsilon$:

$$\begin{aligned} TSTT & = \mathop \sum \limits_{{\left({i,j} \right)}} \left({J_{ij} + \epsilon \cdot K} \right)\left({L_{ij} + M_{ij} \left({J_{ij} +\epsilon \cdot K} \right)} \right) \\ & = \mathop \sum \limits_{{\left({i,j} \right)}} \left({\left[{J_{ij} L_{ij} + M_{ij} J_{ij}^{2}} \right] + \epsilon \cdot K\left[{2M_{ij} J_{ij} + L_{ij} } \right] + \left({\epsilon \cdot K} \right)^{2} \left[{M_{ij}} \right]} \right)^{{}} \\ \end{aligned}$$

which can be written as

$$TSTT = G + H \cdot \epsilon + \left({I \cdot \epsilon} \right)^{2}$$

for appropriate constants G, H, and I, and of these only G and H depend on the toll vector $\tau$ applied.

Therefore, the traveler surplus under any realization $\epsilon$ is:

$$\begin{aligned} TS\left(\epsilon\right) & = \mathop \sum \limits_{r,s} \mathop \int \limits_{0}^{{A_{rs} +\, \epsilon \cdot B}} \left({C_{rs} + \epsilon_{rs} - F_{rs} \omega} \right)d\omega - \left({G + H \cdot \epsilon + \left({I \cdot \epsilon} \right)^{2}} \right) \\ & = \left[{\mathop \sum \limits_{r,s} \left({A_{rs} C_{rs} - \frac{{F_{rs} A_{rs}^{2}}}{2}} \right) - G + A_{rs} \epsilon_{rs}} \right] + \left({\epsilon \cdot B} \right)\mathop \sum \limits_{r,s} \left({C_{rs} + \epsilon_{rs} - F_{rs} \left({A_{rs} + \epsilon \cdot \frac{B}{2}} \right)} \right) - H \cdot \epsilon - \left({I \cdot \epsilon} \right)^{2} \\ \end{aligned}$$

Applying Condition 4, the expected value of TS is thus

$$E\left[{TS}\right] = \left[{\mathop \sum \limits_{r,s} \left({A_{rs} C_{rs} - \frac{{F_{rs} A_{rs}^{2}}}{2}} \right) - G} \right] - \frac{1}{2}\mathop \sum \limits_{r,s} \mathop \sum \limits_{{r^{\prime},s^{\prime}}} \left({\left({F \cdot 1} \right)B_{rs} B_{{r^{\prime}s^{\prime}}} - 2I_{rs} I_{{r^{\prime}s^{\prime}}}} \right)E\left[{\epsilon_{rs} \epsilon_{r^{\prime}s^{\prime}}} \right]$$

Repeating this derivation for the deterministic case when $\epsilon = 0$ gives

$$TS\left( 0 \right) = \left[ {\mathop \sum \limits_{r,s} \left( {A_{rs} C_{rs} - \frac{{F_{rs} A_{rs}^{2} }}{2}} \right) - G} \right]$$

These expressions only differ in the term outside of the brackets in E[TS], but the only terms which depend on the toll vector are A _rs and G. Therefore, when maximizing TS(0) or E[TS] with respect to the link tolls, the objectives differ only by a constant term, and the tolls maximizing TS(0) also maximize E[TS]. □

Example

We use the Pigou–Knight–Downs network, which consists of two parallel links. Link 1 has a constant travel time,$t_{1} = 1,$ and link 2 has travel time equal to its flow, $t_{2} = x$. In the deterministic case, let the demand function be $d = D\left( \kappa \right) = 2 - \kappa$, where $\kappa = { \hbox{min} }(t_{1} , t_{2} )$ is the shortest-path travel time. If a toll of τ is applied to link 2, it is straightforward to see that the solution to this problem is $d = \kappa = 1$, and the total system travel time is $TSTT = \left( {1 - \tau } \right)^{2} + \left( {d - 1 + \tau } \right)$. Since this is an elastic demand problem, the appropriate metric is traveler surplus: $TS = \int_{0}^{d} {D^{ - 1} \left( \omega \right)d\omega - TSTT = d - \frac{1}{2}d^{2} + \tau - \tau^{2} }$. From this expression, the optimal toll is seen to be $\tau * = \frac{1}{2}$, resulting in $TS = \frac{3}{4}$.

We now introduce demand uncertainty by changing the demand function to $D\left( \kappa \right) = 2 + \varepsilon - \kappa$, where ɛ is a random term with zero mean and bounded support $\left[ { - \frac{1}{2},\frac{1}{2}} \right]$. For this distribution of ɛ, both paths will continue to be used at equilibrium, and the solution will be d = 1 + ɛ and $TSTT = \tau^{2} - \tau + \varepsilon + 1$. Therefore, after some simplification, the expected traveler surplus is $E\left( {TS} \right) = \frac{1}{2}E\left( {\varepsilon^{2} } \right) + \frac{1}{2} - \tau^{2} + \tau$, which results in the same optimal toll $\tau^{*} = \frac{1}{2}$, but a slightly different surplus value. In this example, demand uncertainty affects the expected traveler surplus, but not the optimal toll.