Effect of the orientation of the fixed analyzer on the ellipsometric parameters in rotating polarizer and compensator ellipsometer with speed ratio 1:1

Abstract

In a recent work, rotating polarizer compensator ellipsometer (RPCE) with a fixed analyzer was proposed. Three different ellipsometric configurations were presented by considering different speed ratios of the rotating elements. It was shown the speed ratio 1:1 corresponds the minimum error in the calculated optical parameters of c-Si and GaAs samples. In this paper, we investigate the effect of the fixed analyzer alignment on the ellipsometric parameters $\psi$ and $\Delta$ in RPCE structure with speed ratio 1:1 to find out the optimal angle at which the analyzer must be oriented to minimize the uncertainty in the calculated ellipsometric parameters. The uncertainties in the two ellipsometric parameters due to the uncertainties in Fourier coefficients are studied in details and it is found that an analyzer angle in the range $40^{\circ }$–$50^{\circ }$ corresponds to the minimum uncertainty in $\psi$ and $\Delta$ and therefore this range is recommended.

1 Introduction

Because of recent advances in computer technology, the spectroscopic ellipsometry technique has developed rapidly (Tompkins and McGahan 1999; Taya and El-Agez 2011a, b; Tompkins and Irene 2005; El-Agez et al. 2010, 2011a, b, c, d; Aspnes 1973; El-Agez and Taya 2010, 2011a, b, c, 2012; Schubert 2004; Ji-Tao et al. 2012; Qi-Xian et al. 2011; Taya et al. 2011, 2012, 2013a, b; Chen et al. 1994; Taya and El-Agez 2012, 2013a, b; Broch and Johann 2008; Smith 2002). In spectroscopic ellipsometry, characterization techniques including thin-film growth can be performed in real time by employing light as a measurement probe. Ellipsometry is an optical measurement technique that characterizes light reflection (or transmission) from samples. It measures the change in polarization state upon light reflection on a sample. Ellipsometry measures two ellipsometric parameters $\psi$ and $\Delta$ which respectively, represent the amplitude ratio and phase difference between light waves known as p- and s-polarized waves (Taya and El-Agez 2011a; Tompkins and Irene 2005). In ellipsometry, an incidence angle is chosen so that the sensitivity for the measurement is maximized. For semiconductor characterization, the incidence angle is typically 70–80$^\circ$. Spectroscopic ellipsometry has been applied to evaluate optical constants (refractive index $n$ and extinction coefficient $k)$ and thin-film thicknesses of samples.

In ellipsometry, the ellipsometric parameters $(\psi \,\hbox {and}\,\Delta )$ are defined by

$$\begin{aligned} \rho =\frac{r_p }{r_s }=\tan (\psi )e^{i\Delta }, \end{aligned}$$

(1)

where $r_{p}$ and $r_{s}$ are the complex Fresnel coefficients for the p and s light components.

Ellipsometric structures have been proposed and constructed in different configurations in the last two decades. The most common designs were the rotating analyzer ellipsometer (RAE) (Aspnes 1973), rotating polarizer analyzer ellipsometer (RPAE) (El-Agez and Taya 2010, 2011a, b, c, 2012; El-Agez et al. 2010, 2011a, c, d; Schubert 2004; Taya et al. 2011; Ji-Tao et al. 2012; Qi-Xian et al. 2011; Chen et al. 1994; Taya and El-Agez 2012), and the fixed or rotating phase compensator ellipsometer (Taya et al. 2012, 2013a, b; Taya and El-Agez 2013a, b; Broch and Johann 2008; Smith 2002). The RAE contains a fixed polarizer and a rotating analyzer with angular speed $\omega$. The ideal polarizer and analyzer are completely characterized by the azimuth angles $\beta _P$ and $\beta _A ,$ which their transmission axes make with the plane of incidence. In RAE, the azimuth angle $\beta _A$ of the rotating analyzer is written in terms of the angular speed $\omega$ as $\beta _A$ = $\omega {t}$.

RPAE was proposed and experimentally constructed in many forms. The main difference between them was the speed ratio with which the polarizer and the analyzer rotate. The most common configurations were RPAEs with speed ratios 1:1 (El-Agez and Taya 2010; Taya et al. 2013b), 1:2 (El-Agez and Taya 2011a; Chen et al. 1994), 1:3 (Taya et al. 2011, 2012), and 1:-1 (El-Agez et al. 2010).

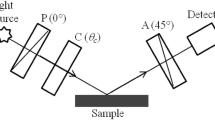
In a recent paper (Taya et al. 2013a), two ellipsometric structures which are rotating polarizer compensator (RPCE) and rotating compensator analyzer (RCAE) were proposed. For each structure, three different configurations were presented by considering different speed ratios. The percent errors arise from noise effects and misalignment of the optical elements were investigated for all configurations. Moreover, the uncertainty in the ellipsometric parameters due to the uncertainty in Fourier coefficients was presented. It is found that in RPCE structure, the speed ratio 1:1 corresponds to the minimum error in the calculated optical parameters of c-Si and GaAs samples. In this ellipsometric configuration, the analyzer was fixed to an azimuth angle $\beta _{A}$.

In this paper, we investigate the effect of the analyzer alignment on the ellipsometric parameters $\psi$ and $\Delta$ in RPCE structure with speed ratio 1:1 to find out the optimal angle at which the fixed analyzer must be oriented to minimize the uncertainty in the calculated ellipsometric parameters.

2 Theory of rotating-element ellipsometer

The Jones vector is defined by the electric field vectors in $x$ and $y$ directions as follow

$$\begin{aligned} E(z,t)=[E_x ,E_y ]^{T}, \end{aligned}$$

(2)

where $T$ indicates the transpose of the matrix and

$$\begin{aligned} \left. {\begin{array}{l} E_x =E_{ox} e^{i\delta _x } \\ E_y =E_{oy} e^{i\delta _y } \\ \end{array}} \right\} , \end{aligned}$$

(3)

where $E_{ox}$ and $E_{oy}$ represent the amplitudes of electric field components and $\delta _x$ and $\delta _y$ are the initial phases of the electric field components.

The total light intensity can be calculated as

$$\begin{aligned} I=E^{*}(z,t)E(z,t). \end{aligned}$$

(4)

The electric vector can be expressed by Stokes vector which has four parameters. The four Stokes parameters of a light beam (which is assumed to be traveling in the $z$-direction) are defined as follows:

$S_{0}$ is the total intensity (or power) of the beam;

$S_{1}$ is the $x$ or horizontal preference, i.e., the excess power in the $x$ linearly polarized component of light over the $y$ polarized component ($x$ and $y$ are orthogonal transverse

axes);

$S_{2}$ is the $x'$ or $45^{\circ }$ preference, i.e., the excess power in the $x'$ linearly polarized component over the $y'$-polarized component, where $x'$ and $y'$ are the bisectors of the $x-y$ coordinate axes; and

$S_{3}$ is the excess power in the right-circularly polarized component over the left-circularly polarized component. It is convenient to lump these parameters in a 4 $\times$ 1 Stokes vector as

$$\begin{aligned} L=[S_0 ,S_1 ,S_2 ,S_3 ]^{T}, \end{aligned}$$

(5)

where $S_{0}$, $S_{1}$, $S_{2}$ and $S_{3 }$ are called the Stokes parameters and the vector $L$ is called the Stokes vector. When we treat totally polarized light, the Jones matrix can be converted to the Mueller matrix which consists of matrix elements similar to those of the Jones matrix. The Mueller matrix calculation is performed in a manner similar to the Jones matrix calculation. In this work, we treat our structure using Mueller formalism. The resultant stokes vector can be determined by multiplying the incident light stokes vector through the Mueller matrices for all elements. The intensity is given by the first element of the resultant stokes vector $S_{0}$. The Mueller formalism gives the same intensity as that obtained by the Jones formalism.

The shape and orientation of the ellipse depends on the angle of incidence, the direction of the polarized incident light, and the reflection properties of the surface. Two parameters $\psi$ and $\Delta$ are determined in one single ellipsometric measurement. This makes it possible to obtain both the real and imaginary parts of the complex dielectric function of a homogeneous material. For a reflecting surface, the forms of $\Delta$ and $\psi$ are given by

$$\begin{aligned} \Delta =\delta _p -\delta _s \ \hbox {and} \ \tan \psi =\frac{\left| {r_p } \right| }{\left| {r_s } \right| }, \end{aligned}$$

(6)

where $\delta _p$ and $\delta _s$ are the phase changes for the $p$ and $s$ components of light. The Fresnel reflection coefficients can be written as

$$\begin{aligned} \left. {\begin{array}{l} r_p =\rho _p e^{i\delta _p } \\ r_s =\rho _s e^{i\delta _s } \\ \end{array}} \right\} . \end{aligned}$$

(7)

The expressions for $r_{p}$ and $r_{s}$ for a single interface between medium 0 (ambient), with a complex refractive index $N_{0}$, and medium 1 (substrate), with a complex refractive index $N_{1}$ are given by

$$\begin{aligned} r_p =\frac{N_1 \cos \theta _0 -N_0 \cos \theta _1 }{N_1 \cos \theta _0 +N_0 \cos \theta _1 },\end{aligned}$$

(8)

$$\begin{aligned} r_s =\frac{N_0 \cos \theta _0 -N_1 \cos \theta _1 }{N_0 \cos \theta _0 +N_1 \cos \theta _1 }, \end{aligned}$$

(9)

where $\theta _{0}$ and $\theta _{1}$ are the angles of incidence and refraction, respectively.

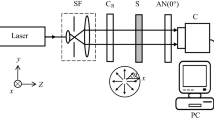
The structure under consideration consists of a fixed polarizer, rotating polarizer with angular speed $\omega$, rotating compensator with the same angular speed, sample, fixed analyzer, and detector. The azimuth angle of the rotating polarizer is assumed to be $\beta _P =\omega {t}$ and that of the rotating compensator is assumed to have the form $\beta _c =\omega {t}$. The fast axis of the analyzer is assumed to have an angle $\beta _A$ with the $p$-polarization. In the rotating polarizer-compensator configuration, the Stokes vector of the detected light is given by

$$\begin{aligned} L=R(-\beta _A ) A R(\beta _A ) S R(-\beta _c ) C R(\beta _c ) R(-\beta _P ) P R(\beta _P ) P L_i , \end{aligned}$$

(10)

where $L_i =[1, 0, 0, 0]^{T}$ and $L$ is the four-element column vector containing Stokes parameters $S_{0}$, $S_{1}$, $S_{2}$, and $S_{3}$.

The matrices shown in Eq. (10) using Mueller formalism that represents the polarizer (analyzer), compensator and the sample to be studied are, respectively, given by

$$\begin{aligned} P&= A=\frac{1}{2}\left[ \begin{array}{cccc} 1&{} 1&{} 0&{} 0 \\ 1&{} 1&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0 \\ \end{array} \right] \end{aligned}$$

(11)

$$\begin{aligned} C&= \left[ \begin{array}{cccc} 1&{} 0&{} 0&{} 0 \\ 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} {\cos (\delta )}&{} {\sin (\delta )} \\ 0&{} 0&{} {-\sin (\delta )}&{} {\cos (\delta )} \\ \end{array} \right] \end{aligned}$$

(12)

$$\begin{aligned} S&= \left[ \begin{array}{cccc} 1&{} {-\cos (2\psi )}&{} 0&{} 0 \\ {-\cos (2\psi )}&{} 1&{} 0&{} 0 \\ 0&{} 0&{} {\sin (2\psi )\cos (\Delta )}&{} {\sin (2\psi )\sin (\Delta )} \\ 0&{} 0&{} {-\sin (2\psi )\sin (\Delta )}&{} {\sin (2\psi )\cos (\Delta )} \\ \end{array} \right] \end{aligned}$$

(13)

Matrix of rotation with an angle $\alpha$, $R(\alpha )$,

$$\begin{aligned} R(\alpha )=\left[ \begin{array}{cccc} 1&{} 0&{} 0&{} 0 \\ 0&{} {\cos (2\alpha )}&{} {\sin (2\alpha )}&{} 0 \\ 0&{} {-\sin (2\alpha )}&{} {\cos (2\alpha )}&{} 0 \\ 0&{} 0&{} 0&{} 1 \\ \end{array} \right] , \end{aligned}$$

(14)

where $\alpha$ may be $\beta _A$, $\beta _C$, or $\beta _P$.

The symbol $\delta$ in the compensator matrix represents the phase difference between the two components of electric field vector through the slow and fast axis that is the light wave parallel to the fast axis propagates faster than that parallel to the slow axis. Knowing that $n_{e}$ and $n_{o }$ are the refractive indices of the two axes and $d$ is the thickness of the compensator then $\delta$ is given by

$$\begin{aligned} \delta =\frac{2 \pi d}{\lambda }(n_e -n_o ). \end{aligned}$$

(15)

Based on Eq. (10), the Fourier transform of the light intensity received by the detector is given by

$$\begin{aligned} I=a_0 +\sum _{n=1}^2 {a_n \cos (2n\omega t)} +\sum _{n=1}^2 {b_n \sin (2n\omega t)} , \end{aligned}$$

(16)

where

$$\begin{aligned} a_o&= 1-\frac{\cos (2\psi )}{2}-\cos (2\psi ) \cos (2\beta _A )+\frac{\cos (2\beta _A )}{2},\end{aligned}$$

(17)

$$\begin{aligned} a_1&= 1-\cos (2\psi )-\cos (2\psi ) \cos (2\beta _A )+\cos (2\beta _A ),\end{aligned}$$

(18)

$$\begin{aligned} a_2&= \frac{\cos (2\beta _A )}{2}-\frac{\cos (2\psi )}{2},\end{aligned}$$

(19)

$$\begin{aligned} b_1&= \sin (2\psi )\cos (\Delta ) \sin (2\beta _A ),\end{aligned}$$

(20)

$$\begin{aligned} b_2&= \frac{\sin (2\psi )\cos (\Delta ) \sin (2\beta _A )}{2}. \end{aligned}$$

(21)

Only three coefficients are required to calculate the ellipsometric parameters. If we consider again $a_{1}$, $a_{2}$ and $b_{1}$ and solve Eqs. (18), (19), and (20), $\psi$ and $\Delta$ can be written as

$$\begin{aligned} \tan (\psi )&= \sqrt{\frac{a_1 }{a_1 -4a_2 }\frac{1-\cos (2\beta _A )}{1+\cos (2\beta _A )}},\end{aligned}$$

(22)

$$\begin{aligned} \cos (\Delta )&= \frac{b_1 }{\sqrt{a_1 }\sqrt{a_1 -4a_2 }}. \end{aligned}$$

(23)

The uncertainties in $\psi$ and $\Delta$ with respect to the Fourier coefficients can be written as

$$\begin{aligned} \frac{\partial \psi }{\partial a_1 }&= \frac{\cot (\psi )}{4\left( {1+\cos (2\beta _A )} \right) }-\frac{\tan (\psi )}{4(1-\cos (2\beta _A ))},\end{aligned}$$

(24)

$$\begin{aligned} \frac{\partial \psi }{\partial a_2 }&= \frac{\tan (\psi )}{(1-\cos (2\beta _A ))},\end{aligned}$$

(25)

$$\begin{aligned} \frac{\partial \cos (\Delta )}{\partial a_1 }&= 2\cos (\Delta )\frac{a_2 }{a_1 (a_1 -4a_2 )},\end{aligned}$$

(26)

$$\begin{aligned} \frac{\partial \cos (\Delta )}{\partial a_2 }&= 2\cos (\Delta )\frac{1}{(a_1 -4a_2 )}, \end{aligned}$$

(27)

and

$$\begin{aligned} \frac{\partial \cos (\Delta )}{\partial b_1 }=\frac{1}{\sqrt{a_1 }\sqrt{a_1 -4a_2 }}=\frac{\cos (\Delta )}{b_1 }. \end{aligned}$$

(28)

3 Results and discussion

In the following calculations, one interface separating an air ambient of refractive index $N_{0}$ and bulk c-Si material of index $N_{1 }$-is assumed. An angle of incidence of $70^{\circ }$ is assumed which is one of the most commonly used angles in spectroscopic ellipsometry. The complex index of refraction of c-Si is taken from the handbook of optical constants of solids (Palik 1985). The complex Fresnel’s coefficients are calculated using Eqs. (8) and (9). A zero order MgF$_{2}$ phase compensator centered at 4 eV is also assumed (Taya et al. 2012, 2013a). The Fourier coefficients are calculated as follows. The complex Fresnel’s coefficients are calculated for the c-Si—air structure assumed and the Stokes vector of the detected light is then calculated using Eq. (10). The four elements in the Stokes vector are denoted as $S_{i}$ $(i=0,1,2,3)$ where the element $S_{0}$ represents the intensity of the signal received by the detector. The Fourier transform of the received signal is taken and the Fourier coefficients $a_{i}$ $(i=0,1,2)$ and $b_{i }(i=1,2)$ are then obtained. The ellipsometric parameters $\psi$ and $\Delta$ are then calculated as a function of the analyzer azimuth angle,$\beta _A$, using Eqs. (22) and (23). The uncertainties in the ellipsometric parameters $\delta \psi$ and $\delta \Delta$ due to the uncertainties of the Fourier coefficients can now be investigated as a function of the incident light energy. $\delta \psi$ and $\delta \Delta$ represent the fluctuations of $\psi$ and $\Delta$ about their ideal values due to the uncertainties of the Fourier coefficients. In real applications of spectroscopic ellipsometry, the uncertainties in the sample parameters such as thickness and index of refraction are of high interest and the uncertainties in $\psi$ and $\Delta$ are of less importance (Aspnes 2004). However, investigation at the sample level is unrealistic due to the large number of possible sample configurations (Aspnes 2004). Therefore, $\delta \psi$ and $\delta \Delta$ are usually used in most cases to introduce the uncertainty in an ellipsometric model. In some cases, the uncertainty is introduced as $\delta \rho =\delta (\tan \psi )+i\delta \Delta \tan \psi$. However, $\delta \rho$ does not reveal the individual contribution of $\delta \psi$ and $\delta \Delta$ and it diverges as $\psi =0^{\circ }$. The uncertainties $\delta \psi$ and $\delta \Delta$ can be calculated using Eqs. (24)–(28). The aim of this work is to find the optimal analyzer alignment at which the uncertainties $\delta \psi$ and $\delta \Delta$ minimize. The uncertainty $\delta \Delta /\delta a_1$ is shown in Fig. 1a for c-Si sample in the photon energy range 1.5–6 eV for $\beta _A = 10^{\circ }$, $20^{\circ }$, $30^{\circ }$, and $45^{\circ }$ whereas Fig. 1b shows the same for $\beta _A \quad =\quad 45^{\circ }$, $60^{\circ }, 70^{\circ }$, and $80^{\circ }$. As can be seen from Fig. 1a, the uncertainty in $\Delta$ due to the uncertainty in the coefficient $a_{1}$ ranges between 0.74 and 4.73 for $\beta _A = 10^{\circ }$, 0.22–3.4 for $\beta _A$ = $20^{\circ }$, 0.14–3.63 for $\beta _A = 30^{\circ }$, and 0.12–5.19 for $\beta _A = 45^{\circ }$. Generally, the range given for $\beta _A$ in Fig. 1a corresponds almost to the same range of $\delta \Delta$ for all values of $\beta _A$. A huge difference can be observed when the alignment of the fixed analyzer increases above $45^{\circ }$ as can be seen from Fig. 1b. $\delta \Delta /\delta a_1$ has the ranges between 0.19 and 10.2 for $\beta _A =60^{\circ }$, 0.36–21.75 for $\beta _A =70^{\circ }$, and 1.3–84.58 for $\beta _A = 80^{\circ }$. The ellipsometric parameter $\Delta$ is given in terms of $a_{1}$, a$_{2}, b_{1}$ as given by Eq.(23). The uncertainties $\delta \Delta /\delta a_1$, $\delta \Delta /\delta a_2$, and $\delta \Delta /\delta b_1$ must be studied in details before we reach a conclusion regarding an optimal alignment of the analyzer in the proposed ellipsometric structure. Figure 2a shows $\delta \Delta /\delta a_2$ for c-Si sample in the photon energy range 1.5–6 eV for $\beta _A = 10^{\circ }, 20^{\circ }, 30^{\circ }$, and $45^{\circ }$. The highest uncertainty of $-2.8$ to $-8.5$ is observed for $\beta _A$ =$10^{\circ }$ while the lowest uncertainty of $-0.17$ to $-0.51$ is obtained for $\beta _A =45^{\circ }$. Figure 2b shows that $\delta \Delta /\delta a_2$ has much lower values for = $60^{\circ }, 70^{\circ }$, and $80^{\circ }$ than those obtained for $\beta _A =10^{\circ }, 20^{\circ }$, and $30^{\circ }$ in Fig. 2a. In general, the uncertainty exhibited by the ellipsometric parameter $\Delta$ to the uncertainty in the coefficient $a_{2}$ is much lower than that exhibited to the uncertainty in $a_{1}$ except for $\beta _A =10^{\circ }$. Moreover, $\delta \Delta /\delta a_2$ for $\beta _A = 45^{\circ }, 60^{\circ }, 70^{\circ }$, and $80^{\circ }$ is very small and can be ignored compared to other uncertainties. To complete the view, $\delta \Delta /\delta b_1$ is plotted as a function of the incident light energy for $\beta _A =10^{\circ }, 20^{\circ }, 30^{\circ }$, and $45^{\circ }$ in Fig. 3a and for $\beta _A = 45^{\circ }, 60^{\circ }, 70^{\circ }$, and $80^{\circ }$ in Fig. 3b. The two panels of Fig. 3 show that the best alignment of the fixed analyzer that corresponds to the minimum uncertainty in is $\beta _A = 45^{\circ }$. On the other hand, the orientation of the analyzer that corresponds to the maximum uncertainty in $\Delta$ due to the uncertainty in $b_{1}$ are $\beta _A = 10^{\circ }$ and $80^{\circ }$.

Fig. 1

The variation in $\Delta$ with respect to $a_{1}$ versus the photon energy from 1.5 to 6 eV for different values of $\beta _{A}$

Fig. 2

The variation in $\Delta$ with respect to $a_{2}$ versus the photon energy from 1.5 to 6 eV for different values of $\beta _{A}$

Fig. 3

The variation in $\Delta$ with respect to $b_{1}$ versus the photon energy from 1.5 to 6 eV for different values of $\beta _{A}$

The ellipsometric parameter $\psi$ is calculated in terms of the coefficients $a_{1}$ and $a_{2}$ as given by Eq. (22). $\delta \psi /\delta a_1$ versus the photon energy is shown in Fig. 4a for $\beta _A = 10^{\circ }, 20^{\circ }$, $30^{\circ }$, and $45^{\circ }$ and in Fig. 4b for $\beta _A = 45^{\circ }, 60^{\circ }$, $70^{\circ }$, and $80^{\circ }$. As Fig. 4a reveals, the uncertainty in $\psi$ due to the uncertainty in $a_{1}$ has the ranges $-1.44$ to 0.07 for $\beta _A = 10^{\circ }$, $-0.30$ to 0.36 for $\beta _A = 20^{\circ }$, $-0.07$ to 0.48 for $\beta _A = 30^{\circ }$, and 0.08 to 0.77 for $\beta _A = 45^{\circ }$. These uncertainties increase considerably when the alignment of the analyzer increases to $70^{\circ }$ and $80^{\circ }$ and take the ranges 0.67–3.34 and 2.76–13.07, respectively, as shown in Fig. 4b. $\delta \psi /\delta a_2$ is illustrated as a function of the photon energy for $\beta _A = 10^{\circ }, 20^{\circ }, 30^{\circ }$, and $45^{\circ }$ in Fig. 5a and for $\beta _A = 45^{\circ }, 60^{\circ }, 70^{\circ }$, and $80^{\circ }$ in Fig. 5b. As can be seen from Fig. 5a, the best orientation of the analyzer is $\beta _A = 45^{\circ }$ in which the uncertainty in $\psi$ ranges between 0.07 and 0.37. On the other hand, $\delta \psi /\delta a_2$ for $\beta _A = 60^{\circ }, 70^{\circ }$, and $80^{\circ }$ is very small and almost in the same range between 0.05 and 0.37 as shown in Fig. 5b.

Fig. 4

The variation in $\psi$ with respect to $a_{1}$ versus the photon energy from 1.5 to 6 eV for different values of $\beta _{A}$

Fig. 5

The variation in $\psi$ with respect to $a_{2}$ versus the photon energy from 1.5 to 6 eV for different values of $\beta _{A}$

To obtain an obvious view of the dependence of the uncertainties of $\psi$ and $\Delta$ on the fixed analyzer orientation, these uncertainties are scanned with the analyzer angle in the range $5^{\circ }$–$85^{\circ }$ in Figs. 6, 7 ,8, 9, 10. The uncertainty in $\Delta$ due to the uncertainty in $a_{1}$ is scanned with $\beta _A$ in Fig. 6. The analyzer angle range from $10^{\circ }$ to $50^{\circ }$ corresponds to the minimum uncertainty in $\Delta$ with a small dependence on the photon energy. The uncertainties obtained for 6 eV are relatively smaller than those obtained for 4 and 2 eV. Figure  7 shows versus $\beta _A$ for photon energies of 2, 4, and 6 eV. As can be seen from the figure, $\beta _A$ of $30^{\circ }$ and above corresponds to the minimum uncertainty in $\Delta$ with an ignorable dependence on the photon energy in this range of $\beta _A$. The variation of $\delta \Delta /\delta b_1$ with $\beta _A$ is plotted in Fig. 8 for different values of the photon energy. An analyzer angles in the range $40^{\circ }$–$50^{\circ }$ correspond to the minimum uncertainty in $\Delta$ due to the uncertainty in $b_{1}$. Moreover, photon energies of 4 and 6 eV are preferable compared to 2 eV. From Figs. 6,7,8, a conclusion can be reached concerning the optimal alignment of the analyzer. An analyzer angle in the range $40^{\circ }$–$50^{\circ }$ corresponds to the minimum uncertainty in $\Delta$ due to the uncertainty in the Fourier coefficients $a_{1}$, $a_{2}$, and $b_{1}$. The high degree of symmetry in Fig. 8 is worth mentioning. The results obtained for $\beta _{A}$ $=$ 10$^{\circ }$ and those obtained for $\beta _{A}$ $=$ 80$^{\circ }$ are identical. In a similar manner, the results obtained for $\beta _{A}$ $=$ 20$^{\circ }$ and those obtained for $\beta _{A}$ $=$ 70$^{\circ }$ are exactly the same, and so on.

Fig. 6

The variation in $\Delta$ with respect to $a_{1}$ versus the analyzer angle $\beta _{A}$ for different values of photon energy

Fig. 7

The variation in $\Delta$ with respect to $a_{2}$ versus the analyzer angle $\beta _{A}$ for different values of photon energy

Fig. 8

The variation in $\Delta$ with respect to $b_{1}$ versus the analyzer angle $\beta _{A}$ for different values of photon energy

Fig. 9

The variation in $\psi$ with respect to $a_{1}$ versus the analyzer angle $\beta _{A}$ for different values of photon energy

Fig. 10

The variation in $\psi$ with respect to $a_{2}$ versus the analyzer angle $\beta _{A}$ for different values of photon energy

Figure 9 shows the scanning of $\delta \psi /\delta a_1$ with $\beta _A$ for different values of the photon energy whereas Fig. 10 shows the same for $\delta \psi /\delta a_2$. Again, an analyzer angle in the range $40^{\circ }$–$50^{\circ }$ can be considered as an optimal orientation that gives a minimum error in $\psi$.

The main contribution of this work was drawn from a specific c-Si/air sample at the incidence angle of $70^{\circ }$. It is worth investigating whether this conclusion is still valid for other samples and other incidence angles. Figure 11 shows the uncertainty in $\Delta$ versus the analyzer angle for a sample consisting of one interface separating an air ambient and bulk GaAs material. The uncertainty in $\Delta$ due to the uncertainty in a $_{1}$ is scanned with $\beta _A$ in the top left panel. The top right panel shows $\delta \Delta /\delta a_2$ versus $\beta _A$ for photon energies of 2, 4, and 6 eV whereas the lower panel shows the variation of $\delta \Delta /\delta b_1$ with $\beta _A$. The same results obtained for the c-Si sample are still observed for the GaAs sample. The analyzer angle range from $40^{\circ }$–$50^{\circ }$ corresponds to the minimum uncertainty in $\Delta$ with a small dependence on the photon energy. The uncertainties obtained for 6 eV are relatively smaller than those obtained for 4 and 2 eV.

Fig. 11

The variation in $\Delta$ with respect to a $_{1}$, a $_{2}$, and b $_{1}$ versus the analyzer angle for a sample consisting of one interface separating an air ambient and bulk GaAs material

On the other hand, Fig. 12 illustrates the scanning of $\delta \psi /\delta a_1$ (top panel) and $\delta \psi /\delta a_2$ (bottom panel) with $\beta _A$ for the GaAs sample. Again, an analyzer angle in the range $40^{\circ }$–$50^{\circ }$ can be considered as an optimal orientation that gives a minimum error in $\psi$.

Fig. 12

The variation in $\psi$ with respect to a $_{1}$ and a $_{2}$ versus the analyzer angle for a sample consisting of one interface separating an air ambient and bulk GaAs material

The uncertainty $\delta \Delta /\delta b_1$ versus the analyzer angle is plotted in Fig. 13 for different incidence angles for c-Si (top panel) and GaAs (bottom panel) samples. As can be seen from the figure, as the angle of incidence increases the curves moves up indicating a barely detectable increase in the uncertainty in $\Delta$. The main aim of this work is to investigate the effect of the fixed analyzer orientation on the ellipsometric parameters. The same conclusion drawn above is still observed in Fig. 13. An analyzer angles in the range $40^{\circ }$–$50^{\circ }$ correspond to the minimum uncertainty in $\Delta$.

Fig. 13

The variation in $\Delta$ with respect to b $_{1}$ versus the analyzer angle for different angles of incidence for c-Si (top panel) and GaAs (bottom panel)

In order to support the conclusion reached in this work, we investigate the uncertainty in the refractive index (n) and extinction factor (k) of the c-Si sample due to the uncertainty in the ellipsometric parameters for different analyzer alignments. Figure 14 shows $\delta n/\delta \psi$ and $\delta k/\delta \psi$ of the c-Si sample for $\beta _A$ $=$ 30$^{\circ }$, 45$^{\circ }$ and 60$^{\circ }$ whereas Fig. 15 shows $\delta n/\delta \Delta$ and $\delta k/\delta \Delta$ for the same analyzer orientations. It can be clearly seen from the two figures that the minimum uncertainty in nand k corresponds to an analyzer angle of $45^{\circ }$ compared to other orientations.

Fig. 14

The uncertainty in the refractive index and extinction factor of the c-Si sample due to the uncertainty in $\psi$ for different analyzer alignments

Fig. 15

The uncertainty in the refractive index and extinction factor of the c-Si sample due to the uncertainty in $\Delta$ for different analyzer alignments

4 Conclusion

Rotating polarizer compensator ellipsometer (RPCE) with speed ratio 1:1 has been investigated in this work. The analyzer was assumed to be fixed at an azimuth angle $\beta _{A}$. The effect of the fixed analyzer azimuth angle on the ellipsometric parameters $\psi$ and $\Delta$ was studied in details to find out the optimal analyzer alignment that corresponds to the minimum uncertainty in $\psi$ and $\Delta$. The ellipsometric parameter $\psi$ was found to depend on two Fourier coefficients whereas $\Delta$ on three. The uncertainties in each ellipsometric parameter due to the uncertainties in the coefficients it depends on were examined in details in the analyzer angle range $\beta _{A} = 10{^{\circ }}$–$80{^{\circ }}$ in the photon energy range 1.5–6 eV. The most important finding was an analyzer angle in the range $40^{\circ }$–$50^{\circ }$ corresponds to the minimum uncertainty in $\psi$ and $\Delta$ and therefore this range is recommended for high accurate rotating polarizer compensator ellipsometer with speed ratio 1:1 and a fixed analyzer.