Bifurcation analysis of 4-axle rail vehicle models in a curved track

Abstract

The article presents authors’ recent results on nonlinear lateral stability of rail vehicles in a curved track. The theories of self-exciting vibrations and bifurcation are the key elements here. The general objective is presentation of extended use of the earlier worked out authors’ method to more complex rail vehicle models. Two 4-axle vehicle models were created. The first one represents coach MKIII described with multibody software by the first author. The second one represents coach 127A described with use of engineering multibody software VI-Rail. The models are described, and method of the analysis is shortly reminded. Then, results for both models are presented. They include verification of the limit cycle possible passage from straight track to circular curve and stability maps for regular curves of different radii and straight track. Next influence of selected suspension parameter and wheel–rail coefficient of friction on vehicle stability is shown. The more general objective is the authors’ say in the hot polemics on the advisability of rail vehicle stability analysis in curves and on the advantages of the nonlinear methods of such analysis over the linear ones.

1 Introduction

Linear models of rail vehicle system were applied at the early stages of stability analysis of such systems (e.g. [47, 48]). The models utilized linear geometry of wheel–rail contact description based on equivalent conicity (e.g. [8, 11]) concept. Recently, the consistent opinion exists that results obtained from linear models may be uncertain to predict features of real object. The linear critical velocity $v_{\mathrm{c}}$ may significantly be bigger than the nonlinear one $v_{\mathrm{n}}$ determined by attractor represented by saddle-node bifurcation point. Some contemporary publications, e.g. [1, 4, 15, 22, 26, 31, 33, 42, 43, 63, 64], develop and systematize the nonlinear mechanics methods in the railway vehicle dynamics. The works deal with straight track (ST) analysis usually, but some of them refer to curved track case. It seems that effective propagation of the nonlinear methods of rail vehicle stability analysis still requires clear and persevering explanations of self-exciting vibrations theory, bifurcation theory and chaos. Confirmation of effectiveness of the nonlinear methods by means of their numerous applications is desired, too.

Rail vehicle dynamics in a curved track is the main interest of this article authors. In particular, this interest is focused on studies of the limit cycles and the stability of motion of rail vehicles in curves. The interest in such scope of study follows the fact that some researchers and railway practitioners still support the opinion that periodic vibrations of constant amplitude (limit cycle) above the critical velocity appear for straight track only. As concerns present authors, the idea of putting the problem of rail vehicles stability in a curved track explicitly was started in [55]. Quite a few detailed questions were formulated in that publication. Two examples are as follows. Does the limit cycle existing in straight track section always disappears while negotiating curved track? Influence of the additional components in equations of motion (serving the curved track case) decreases when curve radius increases. So, does the boundary value of curve radius exist which determines possibility of limit cycle appearance? Many those questions have already been answered thanks to the works of numerous researchers, e.g. [12, 13, 21, 22, 24,25,26, 30,31,32, 34, 35, 38, 40,41,42, 65, 66]. There is also the new question that focuses the authors attention presently. Namely, can nonlinear lateral stability analysis for curved track motion, as that used so many times by them for 2-axle objects ([50,51,52, 62,63,64]), be successfully applied to more complex 4-axle rail vehicle models? To give some answer to this question, the research presented in current paper has been done.

Studies of 4-axle vehicles stability, e.g. [2, 31], seem to be rare comparing to those for the 2-axle ones (e.g. [4, 12, 51, 63, 64]). Studies of nonlinear lateral stability of 4-axle vehicles for the curved track case are particularly rare. Bigger complexity of 4-axle vehicle models makes it expected to get the results different from those for the 2-axle vehicle models.

Because of the above statements, any research to extend knowledge about the issue under consideration seems to be worthy of effort. Consequently, one of the aims in this study has got a cognitive character. It is gathering wider knowledge on stability properties and experience in the stability studies for 4-axle vehicles, especially in a curved track. Besides, some less general issues were of the special interest. They make in fact the detailed aims in this paper. These are: use of the method of the stability analysis as described in [63, 64], for two 4-axle vehicle models; representation of the results on the stability maps as defined for the first time in [50]; and analysis of influence of two factors on the stability of the 4-axle vehicle models, namely of longitudinal stiffness in the secondary suspension and of wheel–rail coefficient of friction. Finally, confrontation of the results for both 4-axle vehicle models was the natural action, too. In particular, it makes possible to compare qualitatively results from the authors own software with those from the commercial one. The subsidiary aim is also to use nonlinear methods of lateral stability analysis as used in rail vehicle dynamics in order to make some contribution into their further dissemination.

2 Theoretical issues and stability method used

2.1 Self-exciting vibrations and bifurcation analysis in rail vehicle dynamics

The self-exciting vibrations theory distinguishes the stable and unstable limit cycles (e.g. [29]). Such cycles occur alternately one after another, and this can happen again and again. In this case, one talks about multiple periodic solutions. The solutions move away from the unstable cycles and tend to the stable ones. Which particular stable cycle is executed—it depends on the initial conditions value. The unstable cycles can be indirectly determined only. Besides, the cycles of soft and hard excitations are referred to. To execute the soft cycle, any initial conditions enable to initiate the self-exciting vibrations provided sufficient amount of energy is delivered into the system. In case of hard excitation some minimum values of initial conditions are additionally necessary to initiate the vibrations. Most of self-exciting vibrations features can be confirmed thorough simulation methods in case of wheelset vibrations in track. Although these results do not make mathematical proof of limit cycles existence, they confirm possibility to apply the self-exciting vibrations theory to explanation of wheelset oscillations. The author’s investigations executed for 2-axle rail vehicle model as well as 4-axle one confirmed the typical limit cycle’s properties in case of wheelset hunting motion. That is, some minimum amount of the energy necessary to initiate the self-exciting vibrations (minimum velocity value), independence of limit cycle parameters from initial conditions, possibility of stable as well as unstable limit cycle determination by means of initial conditions variations. It was also demonstrated that wheelset’s limit cycles for the investigated 2 axle as well as 4-axle vehicles were those ones of hard excitation. Example results for 4-axle railway vehicle are shown in Sect. 5.1.

Fig. 1

Bifurcation plot typical for rail vehicle in circular curve

The Hopf’s bifurcation theory enables to complete and extend interpretation and data of wheelset hunting motion. Most of the corresponding studies focus on straight track motion, e.g. [10, 11, 27, 30, 32, 34, 36, 37, 39, 44]. The bifurcation theory makes it possible to distinguish and explain different values of linear $v_{\mathrm{c}}$ and nonlinear $v_{\mathrm{n}}$ critical velocities. Subcritical bifurcation where $v_{\mathrm{n}} < v_{\mathrm{c}}$ as well as supercritical one where $v_{\mathrm{n}}=v_{\mathrm{c}}$ are specified, e.g. [49]. The bifurcation plots enable to show changes of the chosen vehicle coordinate versus the bifurcation parameter. Analyses of bifurcation plots make fundamental issue in rail vehicle stability analysis since a few dozen years back. The early works are e.g. [10, 14, 17, 18, 27]. The confirmation is also the review paper [20]. Such analysis makes possible to determine position of regions of stable and unstable stationary as well as stable and unstable periodic solutions in relation to each other. Presentation of multiple periodic and stationary solutions as well as chaotic solutions [45] is also possible. The bifurcation plot that might be acknowledged as representative for typical nonlinear model of vehicle-track system of subcritical properties for curved track case is shown in Fig. 1. Leading wheelset lateral displacements $y_{\mathrm{lw}}$ versus bifurcation parameter (vehicle velocity) are shown. The figure is anticipated from bifurcation plot that represents quite often subcritical systems in straight track case [10, 13, 15, 27, 30, 32, 37, 39, 49]. The difficulties with numerical determination of all objects present in Fig. 1 for 2-axle rail vehicles are comprehensively discussed in [64]. Here, we assume that Fig. 1 is valid for some set of typical 4-axle vehicles, too.

In Fig. 1 solid lines represent stable solutions, while dashed lines the unstable ones. Both line types feature stationary and periodic solutions. The point starting off the stable periodic solutions line corresponds to nonlinear critical velocity $v_{\mathrm{n}}$. Critical values of the bifurcation parameter correspond to values of solution for which significant increase or change in type of mathematical model behaviour occurs. Accurate determination of the critical values is an important problem in stability analysis based on bifurcation plots. Velocity $v_{\mathrm{n}}$ separates range of velocity v for which just stable stationary solutions exist, from that for which periodic solutions may additionally appear. For $v< v_{\mathrm{n}}$, one stationary value of the wheelset lateral displacement $y_{\mathrm{lw}}$ exists. In case of straight track the $y_{\mathrm{lw}}=0$, while in case of the curved track $y_{\mathrm{lw}} \ne$ 0 in general. Occurrence of velocity $v_{\mathrm{n}}$ or exciding its value can lead to sudden change of the solution. Periodic form of $y_{\mathrm{lw}}$ may appear. It corresponds to appearance of self-exciting vibrations in the system. In case of hard excitation system, initial conditions of sufficient value are necessary to initiate the vibrations and it corresponds to subcritical Hopf’s bifurcation as shown in Fig. 1. Typical for the subcritical systems is existence of the bifurcation parameter range $v_{\mathrm{n}}< v < v_{\mathrm{c}}$ where stable stationary as well as stable and unstable periodic solutions coexists (Fig. 1). The solutions move away from the unstable periodic solutions line and tend to the stable ones. If the perturbations (initial conditions) are large enough, they tend to stable periodic solutions. If no, then solutions are attracted by the stable stationary branch. The supercritical type of bifurcation appears for the systems of soft excitation. Then $v_{\mathrm{n}}$ and $v_{\mathrm{c}}$ coincide ($v_{\mathrm{n}}=v_{\mathrm{c}})$ and the line of unstable periodic solutions does not exist. Achievement or exceeding the critical value of active parameter v does not mean loss of the stability. The stable periodic solutions above $v_{\mathrm{n}}$ can last for arbitrarily long time (or distance) of simulation when v remains constant. This type of solutions is still preserved for velocities $v > v_{\mathrm{c}}$, becoming the only stable type of solution at the same time. The periodic solutions exist until v achieves the $v_{\mathrm{s}}$ value (Fig. 1). Formally, this point represents loss of stability.

In case of rail vehicle dynamics simulation software, the loss of stability at velocity $v_{\mathrm{s}}$ can have twofold character, sudden or continuous in short time (or distance). Unbounded growth of the oscillations (solutions) occurs in case of the sudden character. The calculations are then usually stopped by the software immediately. Direct reason for such stop are either problems the integration procedure faces or wheel–rail contact lost expressed by too big wheel–rail relative displacements. This type of stability loss happens also for stable stationary solutions. The continuous type of stability loss happens for periodic solutions only. The amplitude and frequency change slowly (so limit cycle character is lost) but calculations can be continued. The minimum velocity value for which some symptoms of non-periodic solution (nor the non-stationary one) appear should be accepted as the $v_{\mathrm{s}}$. The stop at $v_{\mathrm{s}}$ arbitrarily adopted by the software operator is also acceptable, for example, when v becomes unnaturally big but calculations are still possible. Velocity $v_{\mathrm{s}}$ should not be identified with vehicle derailment due to limited projection of the derailment process by means of simulation. Here, the authors call $v_{\mathrm{s}}$ the maximum calculated vehicle velocity, no matter it appears for stationary or periodic solutions and which reason for the calculation stop happens.

Concluding, the search of critical value for bifurcation parameter, and the character and value of the solutions for entire scope of bifurcation parameter changes, makes a subject for the stability studies of nonlinear systems. In the context of rail vehicles, the studies most frequently correspond to lateral dynamics. Wheelsets or car body lateral motion is observed and analysed in velocity domain, up to $v_{\mathrm{s}}$ value. The nonlinearities in vehicle models as e.g. dry friction, bump stops, tables of contact parameters and so on, intensify possibility of the chaotic solutions appearance (e.g. [9, 12, 13, 34, 37, 39, 44, 51]). Consistent opinion exists that studying system’s dynamical properties by means of bifurcation plots creation and analysis is proper way for strongly nonlinear objects of vehicle-track type. Contrary to the above, the critical velocity for linear systems $v_{\mathrm{c}}$ is the only characteristic data (result) when linear vehicle models with linear stability methods are analysed (as commented e.g. in [29, 32]).

2.2 The method of stability analysis exploited in current paper

Principles of the method are adopted from bifurcation approach widely used in the rail vehicle dynamics, e.g. [5, 10, 12, 32, 34, 39, 42, 49]. The method is consistent with the two methods already used by present authors. The first method was used e.g. in [50,51,52, 62] and finally described in [63]. The second method was used and described in [64]. Results from mixed use of both methods can be found in [53, 54]. Also results shown further on can be counted to such type. Due to the detailed description in [63, 64], here rather short discussion of the method is done.

The fundamental difference between both methods is their accuracy. The first method is called the simplified approach, while the second one is referred to as the extended approach. Combined use of both methods regards formal theory of stability. On the other hand, it is less formal than the theory but more practical (faster) instead. It makes careful use of some assumptions and expectations from the system being studied, which are based on the already known general knowledge about the rail vehicle systems. Hence, building the bifurcation plot is the main objective here but complete formal check if the solutions on this plot are formally stable is not such an objective itself. Thanks to it one can omit adoption of some reference solution in the simplified approach. Next, one can omit introduction of different perturbations into the system to check if perturbed solutions remain close to the reference solution. These actions and features are formally required by definition of stability as given in the theory. The approach assumes that any solution typical for railway vehicle systems (stationary or periodic) is stable. Such assumption could be accepted with care based on the understanding within the railway vehicle dynamics that periodic solutions are the self-exiting vibrations that are governed by the tangential forces in wheel–rail contact. Thanks to it, the self-exciting vibrations theory can be used to expect (predict) typical behaviour of the system. When some doubts about stability appear, multiple solutions are suspected, velocity range around critical velocity is just considered, and at random to make sure no mistake is made the formal check of the solution stability (with the dense initial conditions variation to introduce perturbations) is a must. Varying the initial conditions knowingly enables to obtain all multiple solutions for the particular v value. In order to make use of the described approach, some experience in studying rail vehicle stability is indeed desirable. Everyone who decides to use simplifications in the formal approach should remember all the time that it can lead to serious mistakes in determination of critical velocity value and keep at least warnings and explanations from works [43, 64] in mind.

Fig. 2

The scheme of creating a pair of the bifurcation plots for stability analysis in circularly curved track: a basic bifurcation plot, b supplementary bifurcation plot, c stationary solution, and d periodic solution

Fig. 3

Structure of the system nominal model for MKIII coach: a vehicle, b track laterally, and c track vertically

In order to build bifurcation plots, numerous simulations were performed. Their range covers circular curves (CC), from small to large radii R, and straight track (ST), where $R=\infty$. Each single simulation for particular R and adopted initial conditions is done for constant velocity v. The velocity range in succeeding simulations begins at $v=5$ m/s and finish at velocity $v_{\mathrm{s}}$. In the method used the first bogie’s leading wheelset lateral displacements $y_{\mathrm{lw}}$ are observed and recorded. The plots of wheelset lateral displacements versus distance or time were created for a given velocity (Fig. 2c, d). The stable stationary solutions can appear (Fig. 2c) in the system. They typically exist at $v < v_{\mathrm{n}}$. The negative value of $y_{\mathrm{lw}}$ in Fig. 2c, d is a result of adopted orientation of the coordinate systems. The solutions for curves turning to right- and left-hand side are antisymmetric to each other, provided curve radius R and other conditions of motion are identical. To avoid sign problem the maximum absolute value of wheelset lateral displacements ${\vert }y_{\mathrm{lw}}{\vert }$ max is used instead of direct $y_{\mathrm{lw}}$max on the bifurcation plots (Fig. 2a, b). The tested vehicle models are systems of hard excitation. So, some minimum value of perturbation has to be introduced. Here, two methods of initiating vibrations were applied. The first one (being traditional, e.g. [63]) consists in direct imposition of nonzero initial conditions on the wheelsets in CC or ST. In the second one, vibrations are initiated differently in ST and CC. In ST single irregularity of track is used. Vibrations in CCs are caused indirectly by perturbation due to the entrance into preceding transition curve (TC). Figure 2c, d for CC illustrates the second method. Details for both methods are given in Sect. 3.3.

In the author’s approach two parameters, i.e. the maximum of leading wheelset lateral displacements absolute value ${\vert }y_{\mathrm{lw}}{\vert }$ max and peak-to-peak values of the displacements $y_{\mathrm{lw}}$ denoted p-t-p $y_{\mathrm{lw}}$ were read off from each simulation plot.

These two quantities exposed on two complex diagrams as the functions of velocity for entire scope of R (including $R=\infty )$ created a pair of complex bifurcation plots. Such pairs compose so called stability maps [50], being represented here through Figs.  9a–10b. Formally, the stability maps represent stability properties of the system as they show precisely areas of stable and unstable solutions, both the stationary and periodic ones, for entire scope of motion conditions. The crucial elements on the plots are saddle-node and subcritical Hopf’s bifurcations that determine values of nonlinear $v_{\mathrm{n}}$ and linear $v_{\mathrm{c}}$ critical velocities, respectively. Above-mentioned examples of stability maps represent their simplified form, however. They omit unstable solutions and Hopf’s bifurcation point defining $v_{\mathrm{c}}$. This can be done based on knowledge that unstable solutions cannot be observed in real systems. Velocity $v_{\mathrm{c}}$ is of smaller importance in subcritical systems as being bigger than the $v_{\mathrm{n}}$. That is why just the saddle-node bifurcation is of interest on the simplified maps.

Further on the authors extend stability maps notion to the complex bifurcation plots representing stable solutions for ST or particular R value, however, for broad scope of coefficient of friction values. The simplified maps of that type are represented in Figs.  13a–16b.

3 The objects and their models used in the study

Simulation studies within this article were performed utilising two models. The first one exploits the modelling method, mathematical model, and simulation software applied in the earlier studies by first of present authors, e.g. in [57, 59, 60]. The second vehicle model was generated with the commercial engineering software VI-Rail. The vehicle models are supplemented with flexible track models and jointly represent discrete multibody system (MBS) models (composed of rigid bodies) of rail vehicle-track type. Both software implement automatic generation of equations of motion (AGEM) concept. Despite different simulation software, the models have some common features described further on.

3.1 The MKIII coach model

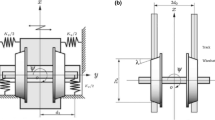
The first model of the 4-axle vehicle has got its real counterpart within British railways rolling stock. It is the MKIII coach. Structure of its nominal (physical) model is shown in Fig. 3a. Structure of the lateral and vertical track nominal models is shown in Fig. 3b, c, respectively. The vehicle-track model has got 38 degrees of freedom (DOFs). That number takes account of: the DOFs in the vehicle model, 6 for each of the 7 bodies; the additional DOFs from the track models, 3 for each of the 4 wheelsets; constraints in the wheelset-track system, 3 for each of the 4 wheelsets; and constraints in the vehicle structure, 2 for each of the 4 wheelsets. The linear spring and damping elements are adopted for the track models as well as primary and secondary suspension of the vehicle model.

The multibody model was generated with the computer code called ULYSSES [3], where dynamics of relative motion is exploited. Vehicle dynamics is the dynamics relative to track-based moving coordinate systems [56, 58,59,60] that are non-inertial in general. Shape of the track is represented by the three-dimensional track centre line described with parametric equations. The full three-dimensional approach is useful in TCs, while in CC and ST it is reduced to special cases of two- and one-dimensional descriptions, respectively. This way the same mathematical and simulation models serve TC, CC and ST cases. The nonlinear kinematics terms and inertia forces due to motion in TC and CC are all taken into account. In the description, Kane’s formalism was applied but adapted [57, 60, 61] to the description in moving reference frames. Thus, second-order ordinary differential equations describe motion of the mechanical system.

Fig. 4

Structure of the system nominal model for 127A coach: a vehicle and track side view, b vehicle and track front view, and c vehicle top view

3.2 The 127A coach model

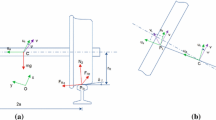
The second 4-axle vehicle model corresponds to 127A coach. This is typical passenger coach within the Polish rolling stock. Bogies of the vehicle have the 25AN Polish designation. The VI-Rail software (ADAMS-Rail formerly) was adopted to create the model. It creates any rail vehicle-track model by assembling typical parts (wheelsets, axle boxes, frames, springs, dampers and any other) and imposing typical constraints on the kinematic pairs. Then equations of motion are generated based on Lagrange’s I type formalism. Structure of the vehicle-track system is shown in Fig. 4a. The model consists of 15 rigid bodies representing the car body, two bogies with two solid wheelsets and eight axle boxes. Each wheelset is attached to axle boxes by joint of revolute type. So rotation of the wheelsets around the lateral axis with respect to axle boxes is possible only. Arm of each axle box is attached to bogie frame by pin joint (pivot - bushing type element). They are laterally, longitudinally and rotary flexible elements. Structure of the lateral and vertical track nominal models is shown in Fig. 4a, b, respectively. The vehicle-track model possesses 82 DOFs.

The linear flexible elements are used in the track model. The linear and nonlinear characteristics in the primary and secondary suspension are used. They represent spiral springs and hydraulic dampers. The nonlinear elements are represented by linear dampers in series with the stiffness (see $c_{1z}$, $c_{2z}$ and $c_{2y}$ in Fig. 4a, b). In addition torsion springs ($k_{\mathrm{bcb}})$ are mounted between car body and bogie frames. To limit car body-bogie frame lateral displacements nonlinear bump stops with 0.03 m clearance were applied (not shown in Fig. 4).

3.3 Common and different features of the models

In case of both models, the wheel–rail contact description includes nonlinear calculation of the tangential contact forces and geometry of wheel and rail profiles. The forces are calculated with the FASTSIM procedure [16], while the geometry with the ArgeCare RSGEO software [19]. In case of MKIII model, results from the RSGEO are tabulated as a function of wheel–rail relative shift. Influence of yaw rotation on the contact parameters was not taken into account in the MKIII coach study. Nominal (not worn) S1002 wheel and UIC60 rail profiles are used in both models.

The track models correspond to a standard European ballasted track of 1435 mm gauge, 1:40 rail inclination, and no geometrical irregularities. Coefficient of friction nominal value in the contact forces calculation equals 0.4 for 127A model and 0.3 for the MKIII one. To check its influence on the stability, these values were varied within the same range, however (Sect. 5.2).

The next common features of both models are as follows. All vehicle-track system elements are the rigid bodies connected to each other by massless springs and dumpers. Each wheelset is supported by a separate track section consisting of two rails and sleepers that cover 1 m of the track length. The wheelset-track particular subsystems are independent from one another. To integrate equations of motion the Gear’s procedure executes the predictor-corrector algorithm in both numerical models. It is suitable to integrate large nonlinear systems of ordinary differential equations of, “stiff type”. The curved track sections had the same parameters while motion in curves was analysed (as in Table 1). The parameter values for vehicles can be found in Table 2 while for the track in Tables 3 and 4 for MKIII and 127A vehicle models, respectively.

Table 1 Curve radii tested and track superelevations corresponding to them

Table 2 Parameters of the analysed models of vehicles

Table 3 Parameters of the track adopted to MKIII coach model

Table 4 Parameters of the track adopted to 127A coach model

Despite similar class of the objects (see Table 2) and similar methods of modelling implemented in both simulation software, there are also many differences. These are, for example, different unchangeable track models predefined in both simulation software. Next is presence of the axle boxes in case of wheelsets modelled in VI-Rail and no such solution in the ULYSSES program. Important difference is the way initial conditions are introduced. In case of ULYSSES program (for MKIII model) the wheelsets are shifted laterally by the same value at the beginning of simulation process. Value of this shift was subject to intensive variation especially around critical velocity and quite often at random, just for check. For noticeable number of velocity values, the shift was equal $y_{\mathrm{lw}}$(0) =$y_{\mathrm{lm}}$(0) =$y_{\mathrm{tm}}$(0) =$y_{\mathrm{tw}}$(0) = 0.0045 m, however. It was determined experimentally by numerous simulations. Values bigger than 0.0045 m do not bring any changes in steady behaviour of the model. This type of the initial conditions imposition can be applied in ST and directly in CC. The second method of initiating vibrations is applied in VI-Rail software (for 127A model). Its use arises from limitations in arbitrary adoption of the initial conditions in this code. Here, singular track lateral irregularity is used located 200 m from route beginning in case of ST stability analysis. It has got half of sine function shape. So, each wheelset is excited laterally when the irregularity is negotiated. The amplitude can obviously vary. In example Fig. 5a, b the amplitude equals 0.006 m and wavelength 20m. In case of CC stability analysis each route is composed of ST section (150 m usually), TC section (150 m usually) and CC of particular radius R. The motion starts in ST and next each wheelset is laterally shifted while entering the TC. This can be enough lateral excitation to initiate self-exciting vibrations in CC if other conditions indispensable to their existence are fulfilled (e.g. Fig. 2d). The main disadvantage of the second method is limited ability of precise variation of the initial conditions in CC. Such variation is useful to detect the potential multiple solutions.

Fig. 5

a Leading wheelset lateral displacements in time domain. Straight track with lateral irregularity and velocity lower than the critical one. b Leading wheelset lateral displacements in time domain. Straight track with lateral irregularity and velocity bigger than the critical one

Taking account of the above differences, the controversy about appearance of hunting in a curved track, so called black box problem in case of commercial codes (no insight into the code), and well known possible considerable differences between results for particular simulation codes (see e.g. benchmark results in [33], concerning $v_{\mathrm{n}}$ values) the authors are interested in qualitative similarities in results for both objects and from both simulation software. Direct benchmarking between the codes, including quantitative issues, is omitted at this stage.

4 Basic results of the stability analysis for 4-axle vehicles

4.1 Self-exiting vibrations for 4-axle vehicles

Fig. 6

Lateral displacement $y_{\mathrm{lw}}$ and its tie derivative for velocity 69 m/s and compound route: a displacement versus distance, b displacement derivative on phase plane, and c displacement derivative magnification for circular curve zone

Simulation studies of the self-exciting vibrations and stability in general for 4-axle vehicles were carried out based on approach used for to 2-axle objects in [63]. Thus, most results in present paper show first bogie leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ versus time or distance. Simulations started in ST. Next, few R values were selected: $R=6000$, 4000, 3000, 2000 and 1200 m. Small velocities v were applied at the beginning for each R. Next v was increased, but each simulation was realised at $v=$ const. All other parameters of the system remained constant, too. So, v was the only parameter determining amount of energy supplied into the system.

Example result confirming some self-exciting vibrations features is presented in Fig. 6. It concerns simulation of 127A model moving along the route composed of: ST, TC and CC of radius $R=2000$ m. Figure 6a shows displacement $y_{\mathrm{lw}}$ versus distance s for velocity $v=$ 69 m/s. In Fig. 6b, c, the same displacement $y_{\mathrm{lw}}$ and its derivative dy $_{\mathrm{lw}}$/dt on phase plane are presented.

The motion starts on a straight, level and ideal track. Thus, $y_{\mathrm{lw}}0$ and dy $_{lw }$d/t = 0 at the beginning. Next the single lateral irregularity of track appears. As a result the nonzero displacements $y_{\mathrm{lw}}$ appear, increase, and take shape of limit cycle in ST. High climb of wheel flange on rail head took place here. It caused some irregularity in the limit cycle shape. Next entrance into TC happened, where vibrations decrease continuously to significantly smaller values. Then short transient behaviour exists in CC initial part. Finally in CC section a region of the limit cycle type solution exists (Fig. 6a, c).

The relation between limit cycle amplitudes in ST and CC can be seen in Fig. 6a. Significantly smaller and unsymmetrically shifted displacements $y_{\mathrm{lw}}$ characterise the motion in CC. In Fig. 6b comparison of the limit cycles in ST and CC on phase plane is done. The initial and TC zones are also shown. The results presented confirm identical physical nature of self-exciting vibrations in a ST and CCs. Thus, the nonlinear critical velocity $v_{\mathrm{n}}$ sense in ST remains valid in CC, too.

Fig. 7

Transformation of limit cycle in ST to limit cycle in CC with passage through TC for $R=2000$ m at $v=20$ m/s. MKIII rail vehicle model

4.2 Appearance of stable periodic solutions in circular curves for MKIII and 127A coaches

First step in the studies for MKIII coach was aimed at checking if this vehicle is capable of hunting in CC. It was done for the zero longitudinal stiffness ($k_{\mathrm{pzx}}$ = 0 N/m) in the secondary suspension. It is known that increasing vehicle suspension’s longitudinal stiffness rises $v_{\mathrm{n}}$. Decreasing it makes $v_{\mathrm{n}}$ lower. The velocity $v_{\mathrm{n}}$ was not formally determined, here. Quite row estimation placed its value between 15 and 20 m/s, however. Finally, the checking simulation was done (Fig. 7) for moderate $R =$ 2000 m and $v=20$ m/s on the route composed of ST, TC and CC. Data of that route are as follows: ST($s_{1~}=$ 150 m), TC ($s_{2~}=$ 180.46 m), CC ($R~=$ 2000 m, $H=$ 0.15 m, $s_{3~}=$ 100 m), where H represents track superelevation s length of the section. The initial conditions for the CC section were specific. They result from limit cycle in ST and self-exciting vibrations still existing in TC. The initial conditions for ST were imposed directly on wheelsets. Thus, $y_{\mathrm{lw}}$(0) = $y_{\mathrm{lm}}$(0) =$y_{\mathrm{tm}}$(0) =$y_{\mathrm{tw}}$(0) = 0.0045 m.

Here and further on the denotations are as follows: y-lateral displacement; indices lw, lm, tm and tw-leading wheelset of front bogie, rear wheelset of front bogie, leading wheelset of rear bogie and rear wheelset of rear bogie, respectively.

One can see fluent passage of the limit cycle in ST to the cycle in CC through the TC in Fig. 7.

The first step in the studies for 127A model is similar to that for MKIII one. Velocity $v_{\mathrm{n}}$ in ST was equal 61.7 m/s. The checking simulation was done (Fig. 8a, b) for $R = 2000$ m and $v =$ 72 m/s on the route composed of ST, TC and CC. Data of that route are as follows: ST ($s_{1 } = 360$ m), TC ($s_{2 } = 120$ m), CC ($R= 2000$ m, $H=0.15$ m, $s_{3}$ > 1000 m). The initial conditions for the CC section were also specific, i.e. adopted similarly as above for MKIII model. But periodic vibrations in ST are response to the lateral track irregularity located 30 m from ST beginning of amplitude 0.006 m and wavelength 20 m.

Fig. 8

a Transformation of limit cycle in ST to limit cycle in CC with passage through TC for R = 2000 m at velocity v= 72 m/s. Front ($y_{\mathrm{lw}})$ and rear ($y_{\mathrm{lm}})$ wheelset of front bogie of 127A rail vehicle model. b Transformation of limit cycle in ST to limit cycle in CC with passage through TC for R = 2000 m at velocity v = 72 m/s. Front ($y_{\mathrm{tw}})$ and rear ($y_{\mathrm{tm}})$ wheelset of rear bogie of 127A rail vehicle model

Passage of the limit cycle in ST to the limit cycle in CC by the TC can be seen for 127A model, too. So, both models have confirmed capability of hunting in CC when the hunting exists in ST section. Note that such a feature is quite often contested by practitioners.

4.3 Stability maps for the MKIII and 127A coach models

The next step in the studies was to check usefulness of the method used by the authors for 2-axle models for 4-axle ones. In order to apply the method from [63] in full, the stability maps were created for both 4-axle vehicle models. The results are presented in Fig. 9a, b for MKIII model and Fig. 10a, b for 127A model.

The differences in comparison to stability maps obtained in [63] for 2-axle vehicle model should be noted. The first one is value of critical velocity $v_{\mathrm{n}}$. In case of 2-axle vehicle model, it was the same value in ST and CCs, usually. Both 4-axle vehicle models manifest differences between $v_{\mathrm{n}}$ in ST and CCs. Velocities $v_{\mathrm{n}}$ in CC sections are bigger than in ST most often (Fig.  9a–10b).

The second difference is influence of curve radius R on $v_{\mathrm{n}}$. Within the R range where it was possible to determine $v_{\mathrm{n}}$ values of R have no influence on $v_{\mathrm{n}}$ in case of 2-axle vehicle model. Both 4-axle vehicle models manifest significant differences in $v_{\mathrm{n}}$ values for different R(Figs. 9a–10b).

The third difference concerns value of maximum lateral displacements ${\vert }y_{\mathrm{lw}}{\vert }$max for v > $v_{\mathrm{n}}$. Generally, for velocity bigger than $v_{\mathrm{n}}$, the bigger R the smaller ${\vert }y_{\mathrm{lw}}{\vert }$max for analogous velocities v in case of 2-axle objects. For the 4-axle object models, the bigger R the bigger ${\vert }y_{\mathrm{lw}}{\vert }$max in case of the 127A model (Fig. 10a). On the other hand ${\vert }y_{\mathrm{lw}}{\vert }$max are close to each other for particular R in case of the MKIII model (Fig. 9a). The peak-to-peak values p-t-p $y_{\mathrm{lw}}$ increase in line with R increase for analogous velocity (Figs. 9b, 10b). It is consistent with the results for 2-axle vehicle model.

Terminal point of each line corresponds to the velocity $v_{\mathrm{s}}$ for which the calculations are stopped due to unbounded growth of oscillations. The velocity $v_{\mathrm{s}}$ increases with rise of R in case of 2-axle vehicle model. It is not the rule in case of the 4-axle models. Velocity $v_{\mathrm{s}}$ for bigger R may be lower than for the smaller one. See $R=3000$ and 2000 m in Fig. 9a, b as well as $R=\infty$ and 6000 m in Fig. 10a, b. It makes the fourth difference in results for the 2- and 4-axle models. Generally, $v_{\mathrm{s}}$ for particular R for 4- axle models are bigger than for 2-axle ones.

Fig. 9

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different R values. MKIII vehicle model. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different R values. MKIII vehicle model

Fig. 10

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different R values. 127A vehicle model. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different R values. 127A vehicle model

The fifth difference is the minimum value of R for which self-exciting vibrations appear. This value was $R=600$ m most often for 2-axle objects. The value equals $R=1200$ m and 2000 m in case of MKIII (Fig. 9a, b) and 127A (Fig. 10a, b) models, respectively. Just stable stationary solutions exist for smaller radii R. Such solutions are of smaller importance here and usually are not presented on the plots.

Above-mentioned differences on stability maps between results for 2- and 4-axle vehicle models change the principles worked out based on the results for 2-axle models only. Namely, the relatively uniform character of the 2-axle models’ properties for all R (including ST) do not prove true in case of 4-axle ones.

5 Investigation into influence of the chosen factors on the stability

5.1 Results of the stability study on a straight track for varying longitudinal stiffness in the secondary suspension

Next in the studies for MKIII coach was determination of $v_{\mathrm{n}}$ in ST for varying values of the suspension stiffness parameters. Finally, value of the longitudinal stiffness $k_{\mathrm{px}}$ in the secondary suspension was varied since variation (increase) of the longitudinal $k_{zx}$ and lateral $k_{zy}$ stiffness in primary suspension did not bring substantial increase of $v_{\mathrm{n}}$. The $k_{\mathrm{px}}$ is longitudinal stiffness of left- and right-hand springs between vehicle body and bogie frame (see Fig. 3a—it is assumed that vertical springs possess flexibility also in the longitudinal and lateral directions). Besides, corresponding values of $v_{\mathrm{s}}$ for the calculation stop were determined. For most cases in figures here and in the next subsection unbounded growth of the solution is connected with the wheel–rail contact lost. In addition, values of ${\vert }y_{\mathrm{lw}}{\vert }$max at velocity $v_{\mathrm{s}}$ were found. The nonzero initial conditions were: $y_{\mathrm{lw}}$(0) = $y_{\mathrm{lm}}$(0) = $y_{\mathrm{tm}}$(0) = $y_{\mathrm{tw}}$(0) = 0.0045 m.

Table 5 Influence of longitudinal stiffness k$_{\mathrm{pzx}}$ in secondary suspension on MKIII vehicle model properties

Fig. 11

Bifurcation plot for MKIII coach with different longitudinal stiffness $k_{\mathrm{pzx}}$ in secondary suspension for straight track case

Results of these investigations are given in Table 5. Velocities $v_{\mathrm{n}}$ and $v_{\mathrm{s}}$ increase with rise of the stiffness $k_{\mathrm{px}}$ in that table. The value $k_{\mathrm{px}}10$ $^{7}$ N/m causes dramatic growth of $v_\mathrm{n}$ up to 180 m/s. Basing on the values of $v_\mathrm{n}$, the $k_{\mathrm{px}}=10$ $^{6}$ N/m resulting in $v_\mathrm{n}$= 36.5 m/s was adopted in the studies of MK 111 coach stability in CCs further on. Considering values of y for any v and at all considered values of $k_{\mathrm{px}}$ building the bifurcation plot in ST for MKIII coach became possible (Fig. 11).

Similar investigations for 127A model, including $v_\mathrm{n}$ determination in ST, were conducted. Finally, value of the longitudinal stiffness $k_{\mathrm{2zx}}$ in the secondary suspension was varied since variation (increase and decrease) of the longitudinal $k_{1\mathrm{x}}$ and lateral $k_{1\mathrm{y}}$ stiffness in primary suspension did not bring substantial increase of $v_{\mathrm{n}}$. The $k_{\mathrm{2zx}}$ is longitudinal stiffness of left- and right-hand springs between vehicle body and bogie frame (see Fig. 4a—as before vertical springs possess flexibility also for longitudinal and lateral directions). Results for $v_{\mathrm{s}}$ and ${\vert }y_{\mathrm{lw}}{\vert }$max at these $v_{\mathrm{s}}$ were found, too.

Results of $k_{\mathrm{2zx}}$ influence on $v_{\mathrm{n}}$, $v_{\mathrm{s}}$ and ${\vert }y_{\mathrm{lw}}{\vert }$max are given in Table 6. Velocities $v_{\mathrm{n}}$ and $v_{\mathrm{s}}$ increase with $k_{\mathrm{2zx}}$ rise. The value of $k_{\mathrm{2zx}}$ = 16$\times$10$^{6}$ causes significant growth of $v_{\mathrm{n}}$ up to 276 m/s. The $v_{\mathrm{s}}$ value achieves more than 300 m/s in this case. Value of$k_{2zx }$= 16$\times$10$^{4}$ N/m (resulting in $v_{n }$= 61.7 m/s) was adopted as a nominal value in the studies of 127A coach stability in CCs further on. Considering values of y for any v and at all values of $k_{\mathrm{2zx}}$ the bifurcation plot in ST for 127A coach was built (Fig. 12).

Table 6 Influence of longitudinal stiffness k$_{\mathrm{2zx}}$ in secondary suspension on 127A vehicle model properties

Fig. 12

Bifurcation plot for 127A coach with different longitudinal stiffness $k_{\mathrm{2zx}}$ in secondary suspension for straight track case

Fig. 13

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. Straight track motion of MKIII coach model. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. Straight track motion of MKIII coach model

5.2 Results of the study on coefficient of friction influence on vehicle models stability properties in straight and curved track

Last to discuss is the assessment of influence of wheel–rail coefficient of friction $\mu$ on vehicle stability. It is well known that $\mu$ is a key parameter in the methods of tangential forces calculation (the more practical counterpart of $\mu$ is coefficient of adhesion). Numerical algorithms calculating the tangential contact forces accept constant predefined value of $\mu$ usually. On the other hand experiments in real system reveal significant range of possible changes of $\mu$ [28]. Additionally, the third body layer (e.g. leaves or iron oxides) may separate the bulk materials in the wheel–rail contact. So the wheel and rail material properties in real conditions may significantly differ from these in clean state (laboratory conditions). The lower value of $\mu$ is about 0.1 (wet surfaces covered by iron oxides and organic substance). The maximum $\mu$ value may exceed 1.0 (dry surfaces and sand delivered between wheel and rail). The weather conditions influence $\mu$ due to an open nature of railway system. So both, the underestimation and overestimation of $\mu$ during vehicle-track model analysis can happen. Accurate adoption of $\mu$ value plays significant role in modelling rail vehicle dynamics. It may reduce operational and maintenance costs and increase safety in the long term as vehicle performance is more precisely anticipated [23].

The lateral displacement $y_{\mathrm{lw}}$ for both 4-axle vehicle models is the parameter in view, here. To check influence of wide range of $\mu$ values on rail vehicle stability 48 series of simulations were executed. For $\mu$ increased from 0.1 to 0.8 with the 0.1 step series of simulations for $R=3000$, 6000 m and $\infty$ (ST) have been done. Each series consists of a few dozen simulations for constant v. The initial v value was 10 m/s usually. On the other hand, the stable stationary solutions exist for such value most often. Therefore, the results for $v \quad>$ 20 or 40 m/s are presented. Velocity v is increased in each next simulation (executed for a given $\mu$) by the 2 m/s step. In case of sudden changes of the solution value or character the step was dropped to 0.1 m/s.

Results for ST are shown at first. These are Figs. 13a, b and 14a, b for MKIII and 127A coaches, respectively. Each line corresponds to particular $\mu$ value. The similarities for both models are of the primary interest.

Fig. 14

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. Straight track motion of 127A coach model. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. Straight track motion of 127A coach model

Fig. 15

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach MKIII curved track motion for $R=$6000 m radius. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach MKIII curved track motion for $R=$6000 m radius

Velocity $v_{\mathrm{n}}$ changes in the range $v_{\mathrm{n}}=36.5$ to 38.5 m/s for the MKIII model and $v_{\mathrm{n}}=58$ to 63.3 m/s for the 127A model. So, small influence of $\mu$ on $v_{\mathrm{n}}$ exists. Just stable periodic solutions exist for $v > v_{\mathrm{n}}$ and no bifurcation to other type solutions appears. Increase of ${\vert }y_{\mathrm{lw}}{\vert }$max and p-t-p $y_{\mathrm{lw}}$ values with $\mu$ increase can be observed. Significant influence of $\mu$ on velocity $v_{\mathrm{s}}$ is visible. In case of $\mu =0.1$ to 0.3 the $v_{\mathrm{s}}$ achieves 140 to 150 m/s for MKIII model, while exceeds 200 m/s in case of 127A model. The simulations were stopped at 200 m/s (720 km/h) as being too unrealistic for the real system. Significant decrease of $v_{\mathrm{s}}$ can be observed for $\mu =0.4$ to 0.8. Velocity $v_{\mathrm{s}}$ is just several m/s higher than $v_{\mathrm{n}}$ for big $\mu =0.7$ to 0.8. It means quite dangerous situation may appear in real system when $v_{\mathrm{n}}$ is achieved. Exceeding $v_{\mathrm{n}}$ slightly can bring in the danger of vehicle derailment.

Fig. 16

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach 127A curved track motion of radius $R=6000$ m. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach 127A curved track motion of radius $R=$6000m

Fig. 17

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach MK111 curved track motion for R = 3000 m radius. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach MKIII curved track motion for R = 3000 m radius

The CC case of big $R=6000$ m is presented in Fig. 15a, b for MKIII model and in Fig. 16a, b for 127A model. Smaller number of similarities can be noticed when current two pairs of bifurcation plots are observed in comparison to ST case. Stable stationary solutions exist for $v < v_{\mathrm{n}}$ for both models. It means that p-t-p $y_{\mathrm{lw}}=0$ but ${\vert }y_{\mathrm{lw}}{\vert }$max $\ne$ 0, usually. Periodic solutions appear at $v_{\mathrm{n}}=28$ m/s for $\mu$ > 0.5 in case of MKIII model (Fig. 15a, b). The corresponding p-t-p $y_{\mathrm{lw}}$ values are very small (up to 0.0018 m). For $\mu =0.1$ to 0.4 stable periodic solutions appear at $v_{\mathrm{n}}=43$ to 48 m/s, respectively. Such separation in $\mu$ influence on $v_{\mathrm{n}}$ value is not observed in case of 127A model (Fig. 16a, b). The stable periodic solutions appear at $v_{\mathrm{n}}$ range between 62 and 74 m/s, depending on $\mu$ value. No regularity of $v_{\mathrm{n}}$ dependence on $\mu$ value can be observed, however. The $v_{\mathrm{n}}$ achieves minimum for $\mu$ = 0.1 and maximum for $\mu$ = 0.6. Just stable periodic solutions exist for $v > v_{\mathrm{n}}$ and $\mu$ $\ge$ 0.5. For $\mu$ < 0.5 and $v > v_{\mathrm{n}}$ bifurcations from periodic solutions to stable stationary ones appear. Values of ${\vert }y_{\mathrm{lw}}{\vert }$max are relatively small at these moments, so no danger of the derailment occurs in the real system. Values of $v_{\mathrm{s}}$ decrease significantly, while $\mu$ is increasing in case of both models.

Fig. 18

a Part one of stability map—maximum of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach 127A curved track motion for R = 3000 m radius. b Part two of stability map—peak-to-peak value of leading wheelset’s lateral displacement $y_{\mathrm{lw}}$ for different $\mu$ values. The coach 127A curved track motion for R = 3000 m radius

The CC case for smaller R = 3000 m is illustrated in Figs. 17a, b and 18a, b for MKIII and 127A coaches, respectively. Velocities $v_{\mathrm{n}}$ for particular $\mu$ values appear between 58.5 and 59.5 m/s in case of MKIII coach model (Fig. 17a, b). So, width of the $v_{\mathrm{n}}$ range is smaller than for R = 6000 m. On the other hand, the range of $v_{\mathrm{n}}$ is between 55.4 and 72 m/s in case of 127A coach model (Fig. 18a, b). So, width of the $v_{\mathrm{n}}$ range is bigger than for R = 6000 m. Both models are subject to increase of ${\vert }y_{\mathrm{lw}}{\vert }$max and p-t-p $y_{\mathrm{lw}}$ with the $\mu$ increase. The bifurcations to stationary solutions appear for small $\mu$ value in case of both models, too. Also velocities $v_{\mathrm{s}}$ decrease while $\mu$ is increasing. This dependence is significantly stronger for MKIII coach, however. For maximum value of $\mu$ = 0.8 the $v_{\mathrm{s}}$ is even equal to $v_{\mathrm{n}}$ for MKIII model.

6 Conclusion

The method of rail vehicle stability analysis in a curved track presented in [63], extended in [64], and applied to 2-axle objects was shortly remained in present article. Here, that method was successfully extended to analysis of 4-axle rail vehicle models. In terms of the technique of study, no additional difficulty was observed, provided the lateral displacements of leading wheelset in the front bogie $y_{\mathrm{lw}}$ are chosen as a subject of the analysis. Study on stability of rail vehicle model through observation of appearance of self-exciting vibrations and model elements behaviour is recently the effective method for multibody systems of that type [20]. Some inevitable, so acceptable trouble is increase of the calculation time for 4-axle vehicles due to more DOFs. In view of that, the standard method of analysis, being more efficient, rather than extended method, as both named in [64] is recommended. To apply the standard method, one should be aware of possibility of multiple solutions existence. They are more probable than in case of a 2-axle vehicle, especially when numerous or severe nonlinearities in a 4-axle vehicle model exist. Going further, it should be mentioned that results presentation of the stability analysis on the stability maps was possible for the 4-axle vehicles in terms of practice. It appears equally useful as for 2-axle vehicles, when one is interested in stability analysis in CCs.

Two kinds of the software were used to check the possibility to apply the research method to 4-axle vehicle models. The first one was individual software by the first author. The second one was created with help of widely used engineering tool VI-Rail. The created models differ from each other in vehicles described and modelling details, so the results differ also qualitatively. Nevertheless, both models confirm the possibility of stability analysis with application of the proposed method. Self-exciting vibrations appear for velocity bigger than some characteristic value for ST and CCs as well. Both models confirm possibility of limit cycle transformation from ST to CC with passage through TC. But critical velocity $v_{\mathrm{n}}$ for ST is different than for CCs (is smaller usually). Curve radius R has influence on $v_{\mathrm{n}}$ value. So, the 4-axle vehicle models do not present as homogenous features as the 2-axle models tested previously.

It was also possible to use the method to examine influence of the two factors on the stability properties of the 4-axle vehicles. They are the longitudinal stiffness in secondary suspension and wheel–rail coefficient of friction. The other factor, namely track gauge, was studied by the authors in [6, 54]. So, the analysis from point of view of such influences as performed 2-axle vehicles (e.g. [7, 51, 53, 62, 63]) appeared successful for 4-axle vehicles. Most of the models’ parameters have smaller or bigger influence on critical velocity $v_{\mathrm{n}}$, maximum calculated velocity $v_{\mathrm{s}}$ and character of solutions between these values. The results for variation of longitudinal stiffness $k_{\mathrm{px}}$ (and $k_{\mathrm{2zx}})$ in secondary suspension reveal moderate influence of it lower values on the vehicle model properties. For the higher values of this parameter, dramatic growth of $v_{\mathrm{n}}$ and $v_{\mathrm{s}}$ appears. The coefficient of friction $\mu$ between wheel and rail may change significantly in real conditions. Both 4-axle vehicle models manifest moderate influence of $\mu$ on velocity $v_{\mathrm{n}}$ in ST. On the other hand, significant influence on $v_{\mathrm{s}}$ can be observed in ST. This is the case especially in the $\mu$ range from 0.3 to 0.5. In case of CC sections, value of $\mu$ has much stronger influence on the stability properties of the studied vehicles. The differences in velocity $v_{\mathrm{n}}$ and maximum lateral displacement $y_{\mathrm{lw}}$ are definitely bigger for different $\mu$ in CCs. Also the shape and character of the quantities on the stability maps differ for $v > v_{\mathrm{n}}$ significantly more in CCs than in ST.

Comparing the results for both analysed 4-axle objects, some general qualitative similarity of the stability maps might be undoubtedly formulated (compare Figs. 9a, b with 10a, b). Quantitatively, the difference between values of ${\vert }y_{\mathrm{lw}}{\vert }$max and p-t-p $y_{\mathrm{lw}}$ for ST and CCs is much bigger for 127A coach at the same time. Critical velocities $v_{\mathrm{n}}$ for MKIII and 127A coaches differ significantly in ST. Velocity $v_{\mathrm{n}}$ for MKIII coach is much smaller. Besides, it differs from values of $v_{\mathrm{n}}$ for CCs more than for 127A coach, too. It is in part result of the adopted values of suspension parameters and in part of the structure.