Skip to main content

Advertisement

SpringerLink
Log in

Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

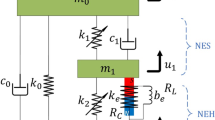
A novel nonlinear structure with adjustable stiffness, damping and inertia is proposed and studied for vibration energy harvesting. The system consists of an adjustable-inertia system and X-shaped supporting structures. The novelty of the adjustable-inertia design is to enhance the mode coupling property between two orthogonal motion directions, i.e., the translational and rotational directions, which is very helpful for the improvement of the vibration energy harvesting performance. Weakly nonlinear stiffness and damping characteristics can be introduced by the X-shaped supporting structures. Combining the mode coupling effect above and the nonlinear stiffness and damping characteristics of the X-shaped structures, the vibration energy harvesting performance can be significantly enhanced, in both the low frequency range and broadband spectrum. The proposed 2-DOF nonlinear vibration energy harvesting structure can outperform the corresponding 2-DOF linear system and the existing nonlinear harvesting systems. The results in this study provide a novel and effective method for passive structure design of vibration energy harvesting systems to improve efficiency in the low frequency range.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Stephen, N.G.: On energy harvesting from ambient vibration. J. Sound Vib. 293, 409–425 (2006)

    Article  Google Scholar 

  2. Harne, R.L., Wang, K.W.: A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 22, 023001 (2013)

    Article  Google Scholar 

  3. Chen, Z.S., Guo, B., Yang, Y.M., Cheng, C.C.: Metamaterials-based enhanced energy harvesting: a review. Phys. B 438, 1–8 (2014)

    Article  Google Scholar 

  4. Roundy, S., Wright, P.K., Rabaey, J.: A study of low level vibrations as a power source for wireless sensor nodes. Comput. Commun. 26, 1131–1144 (2003)

    Article  Google Scholar 

  5. Miller, L.M., Halvorsen, E., Dong, T., Wrigh, P.K.: Modelling and experimental verification of low frequency MEMS energy harvesting from ambient vibrations. J. Micromech. Microeng. 21, 045029 (2011)

    Article  Google Scholar 

  6. Ramlan, R., Brennan, M.J., Mace, B.R., Kovacic, I.: Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 59, 545–558 (2010)

    Article  MATH  Google Scholar 

  7. Cottone, F., Vocca, H., Gammaitoni, L.: Nonlinear energy harvesting. Phys. Rev. Lett. 102, 080601 (2009)

    Article  Google Scholar 

  8. McInnesa, C.R., Gormana, D.G., Cartmell, M.P.: Enhanced vibrational energy harvesting using nonlinear stochastic resonance. J. Sound Vib. 318, 655–662 (2008)

    Article  Google Scholar 

  9. Mann, B.P., Sims, N.D.: Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 319, 515–530 (2009)

    Article  Google Scholar 

  10. Stanton, S.C., Owens, B.A.M., Mann, B.P.: Harmonic balance analysis of the bistable piezoelectric inertial generator. J. Sound Vib. 331, 3617–3627 (2009)

    Article  Google Scholar 

  11. Stanton, S.C., McGehee, C.C., Mann, B.P.: Nonlinear dynamics for broadband energy harvesting: investigation of a bistable piezoelectric inertial generator. Phys. D 239, 640–653 (2010)

    Article  MATH  Google Scholar 

  12. Erturk, A., Inman, D.J.: Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 330, 2339–2353 (2011)

    Article  Google Scholar 

  13. Wu, Z., Harne, R.L., Wang, K.W.: Energy harvester synthesis via coupled linear-bistable system with multistable dynamics. J. Appl. Mech. 81, 061005 (2014)

    Article  Google Scholar 

  14. Renno, J.M., Daqaq, M.F., Inman, D.J.: On the optimal energy harvesting from a vibration source. J. Sound Vib. 320, 386–405 (2009)

    Article  Google Scholar 

  15. Harne, R.L., Wang, K.W.: Prospects for nonlinear energy harvesting systems designed near the elastic stability limit when driven by colored noise. J. Vib. Acoust. 136(2), 021009 (2014)

    Article  Google Scholar 

  16. Tehrani, M.G., Elliott, S.J.: Extending the dynamic range of an energy harvester using nonlinear damping. J. Sound Vib. 333, 623–629 (2014)

    Article  Google Scholar 

  17. Ma, T.W., Zhang, H., Xu, N.S.: A novel parametrically excited non-linear energy harvester. Mech. Syst. Signal Process. 28, 323–332 (2012)

    Article  Google Scholar 

  18. Vijayan, K., Woodhouse, J.: Shock transmission in a coupled beam system. J. Sound Vib. 332, 3681–3695 (2013)

    Article  Google Scholar 

  19. Vijayan, K., Woodhouse, J.: Shock amplification, curve veering and the role of damping. J. Sound Vib. 333, 1379–1389 (2014)

    Article  Google Scholar 

  20. Vijayan, K., Friswell, M.I., Khodaparast, H.H., Adhikari, S.: Non-linear energy harvesting from coupled impacting beams. Int. J. Mech. Sci. 96–97, 101–109 (2015)

    Article  Google Scholar 

  21. Babitsky, V.I.: Theory of Vibro-Impact Systems and Applications. Springer, Berlin (1998)

    Book  MATH  Google Scholar 

  22. Liu, J.Q., Fang, H.B., Xu, Z.Y., Mao, X.H., Shen, X.C., Chen, D., Chen, D., Liao, H., Cai, B.C.: A MEMS-based piezoelectric power generator array for vibration energy harvesting. Microelectron. J. 39, 802–806 (2008)

    Article  Google Scholar 

  23. Marinkovic, B., Koser, H.: Demonstration of wide bandwidth energy harvesting from vibrations. Smart Mater. Struct. 21, 065006 (2012)

    Article  Google Scholar 

  24. Kim, I.H., Jung, H.J., Lee, B.M., Jang, S.J.: Broadband energy-harvesting using a two degree-of-freedom vibrating body. Appl. Phys. Lett. 98, 214102 (2011)

    Article  Google Scholar 

  25. Jang, S.J., Rustighi, E., Brennan, M.J., Lee, Y.P., Jung, H.J.: Design of a 2DOF vibrational energy harvesting device. J. Intell. Mater. Syst. Struct. 22, 443–449 (2011)

    Article  Google Scholar 

  26. Liu, C.C., Jing, X.J.: Vibration energy harvesting with a nonlinear structure. Nonlinear Dyn. 84, 2079–2098 (2016)

    Article  MathSciNet  Google Scholar 

  27. Liu, C.C., Jing, X.J., Li, F.M.: Vibration isolation using a hybrid lever-type isolation system with an X-Shape supporting structure. Int. J. Mech. Sci. 98, 169–177 (2015)

    Article  Google Scholar 

  28. Sun, X.T., Jing, X.J.: Analysis and design of a nonlinear stiffness and damping system with a scissor-like structure. Mech. Syst. Signal Process. 66–67, 723–742 (2016)

    Article  Google Scholar 

  29. Rahimia, A., Zorlu, O., Muhtaroglu, A., Kulah, H.: An electromagnetic energy harvesting system for low frequency applications with a passive interface ASIC in standard CMOS. Sens. Actuators A 188, 158–166 (2012)

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support from a GRF Project of Hong Kong RGC (Ref No.15206514), NSFC Projects (No 61374041 and 11402067) of China, a grant from the Innovation and Technology Commission of the HKSAR Government to the Hong Kong Branch of National Rail Transit Electrification and Automation Engineering Technology Research Center, and internal Research Grants of Hong Kong Polytechnic University.

Author information

Authors and Affiliations

  1. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, People’s Republic of China

    Chunchuan Liu

  2. Department of Mechanical Engineering, Hong Kong Polytechnic University, Kowloon, Hong Kong

    Chunchuan Liu & Xingjian Jing

  3. Hong Kong Branch of National Rail Transit Electrification and Automation Engineering Technology Research Center, Hong Kong, People’s Republic of China

    Chunchuan Liu & Xingjian Jing

  4. Hong Kong Polytechnic University Shenzhen Research Institute, Shenzhen, People’s Republic of China

    Chunchuan Liu & Xingjian Jing

Authors
  1. Chunchuan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xingjian Jing
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xingjian Jing.

Appendix

Appendix

$$\begin{aligned} \Gamma _{11}= & {} \frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$
(26)
$$\begin{aligned} \Gamma _{12}= & {} \frac{4d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}, \end{aligned}$$
(27)
$$\begin{aligned} \Gamma _{20}= & {} \frac{6\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{6\tan \theta _2 }{(2n_2 +1)^{2}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned} \Gamma _{21}= & {} \frac{6d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{6d_2^2 \tan \theta _2 }{(2n_2 +1)^{2}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} \Gamma _{22}= & {} \frac{6d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{6d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned} \Gamma _{30}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2\left( {3-2\cos 2\theta _2 } \right) }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned} \Gamma _{31}= & {} \frac{2d_1^2 \left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2d_2^2 \left( {3-2\cos 2\theta _2 } \right) }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$
(32)
$$\begin{aligned} \Gamma _{32}= & {} \frac{2d_2 \left( {3-2\cos 2\theta _2 } \right) }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2d_1 \left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$
(33)
$$\begin{aligned} \Gamma _{33}= & {} \frac{2d_2^3 \left( {3-2\cos 2\theta _2 } \right) }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2d_1^3 \left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$
(34)
$$\begin{aligned} \Pi _{10}= & {} \frac{4d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}, \end{aligned}$$
(35)
$$\begin{aligned} \Pi _{11}= & {} \frac{4d_1^2 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4d_2^2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$
(36)
$$\begin{aligned} \Pi _{20}= & {} \frac{6d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{6d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$
(37)
$$\begin{aligned} \Pi _{21}= & {} \frac{6\tan \theta _2 d_2^3 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{6\tan \theta _1 d_1^3 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$
(38)
$$\begin{aligned} \Pi _{22}= & {} \frac{6d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 }+\frac{6d_2^2 \tan \theta _2 }{(2n_2 +1)^{2}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$
(39)
$$\begin{aligned} \Pi _{30}= & {} \frac{2\left( {3-2\cos 2\theta _2 } \right) d_2 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2\left( {3-2\cos 2\theta _1 } \right) d_1 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$
(40)
$$\begin{aligned} \Pi _{31}= & {} \frac{2\left( {3-2\cos 2\theta _2 } \right) d_2^3 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{2\left( {3-2\cos 2\theta _1 } \right) d_1^3 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$
(41)
$$\begin{aligned} \Pi _{32}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) d_1^2 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2\left( {3-2\cos 2\theta _2 } \right) d_2^2 }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$
(42)
$$\begin{aligned} \Pi _{33}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) d_1^4 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{2\left( {3-2\cos 2\theta _2 } \right) d_2^4 }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\nonumber \\ \end{aligned}$$
(43)
$$\begin{aligned} \Lambda _{01}= & {} \frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$
(44)
$$\begin{aligned} \Lambda _{02}= & {} \frac{4d_2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4d_1 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}, \end{aligned}$$
(45)
$$\begin{aligned} \Lambda _{11}= & {} \frac{8\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{8\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 },\nonumber \\ \end{aligned}$$
(46)
$$\begin{aligned} \Lambda _{12}= & {} \frac{8d_2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{8d_1 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$
(47)
$$\begin{aligned} \Lambda _{20}= & {} \frac{4(1+3\sin ^{2}\theta _1 )}{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{4(1+3\sin ^{2}\theta _2 )}{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 },\nonumber \\ \end{aligned}$$
(48)
$$\begin{aligned} \Lambda _{21}= & {} \frac{4(1+3\sin ^{2}\theta _1 )d_1^2 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{4(1+3\sin ^{2}\theta _2 )d_2^2 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }, \nonumber \\\end{aligned}$$
(49)
$$\begin{aligned} \Lambda _{22}= & {} \frac{4(1+3\sin ^{2}\theta _2 )d_2 }{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{4(1+3\sin ^{2}\theta _1 )d_1 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }. \nonumber \\\end{aligned}$$
(50)
$$\begin{aligned} {\Lambda }'_{01}= & {} \frac{4d_1^2 \tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4d_2^2 \tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$
(51)
$$\begin{aligned} {\Lambda }'_{11}= & {} \frac{8d_1^2 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }+\frac{8d_2^2 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }, \nonumber \\\end{aligned}$$
(52)
$$\begin{aligned} {\Lambda }'_{12}= & {} \frac{8d_2^3 \tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }-\frac{8d_1^3 \tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\nonumber \\ \end{aligned}$$
(53)
$$\begin{aligned} {\Lambda }'_{21}= & {} \frac{4(1+3\sin ^{2}\theta _1 )d_1^4 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }+\frac{4(1+3\sin ^{2}\theta _2 )d_2^4 }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }, \nonumber \\\end{aligned}$$
(54)
$$\begin{aligned} {\Lambda }'_{22}= & {} \frac{4(1+3\sin ^{2}\theta _2 )d_2^3 }{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }-\frac{4(1+3\sin ^{2}\theta _1 )d_1^3 }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\nonumber \\ \end{aligned}$$
(55)

where the coefficients \(\Gamma _{11}\), \(\Gamma _{12}\), \(\Gamma _{20}\), \(\Gamma _{21}\), \(\Gamma _{22}\), \(\Gamma _{30}\), \(\Gamma _{31}\), \(\Gamma _{32}\), \(\Gamma _{33}\), \(\Pi _{10}\), \(\Pi _{11}\), \(\Pi _{20}\), \(\Pi _{21}\), \(\Pi _{22}\), \(\Pi _{30}\), \(\Pi _{31}\), \(\Pi _{32}\), \(\Pi _{33}\), \(\Lambda _{01}\), \(\Lambda _{02}\), \(\Lambda _{11}\), \(\Lambda _{12}\), \(\Lambda _{20}\), \(\Lambda _{21}\), \(\Lambda _{22}\), \({\Lambda }'_{01}\), \({\Lambda }'_{11} \), \({\Lambda }'_{12}\), \({\Lambda }'_{21} \) and \({\Lambda }'_{22} \) listed in Appendix A are the constant coefficients composed by the structure parameters \(n_{1}\), \(n_{2}\), \(d_{1}\), \(d_{2}\), \(\theta _{1}\) and \(\theta _{2}\).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Jing, X. Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia. Nonlinear Dyn 88, 79–95 (2017). https://doi.org/10.1007/s11071-016-3231-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3231-1

Keywords

Search

Navigation