1 Introduction

A vibration isolator typically includes a spring and a parallel viscous damper, and typically mounted between the vibration sources and equipment to reduce the unwanted excitations. A well-documented dilemma of these linear isolators is that the viscous damping suppresses the resonance amplitude of the vibration transmissibility curve but at the cost of degrading its isolation performance at high frequencies. Thus, a compromise has to be made according to practical requirements. Early studies [1] showed that the implementation of nonlinear damping may bring improvements to the isolation performance of a lightly linear damped isolator by suppressing its resonance amplitude without degrading its high-frequency isolation efficiency. Recent rigorous theoretical works [2,3,4,5] also pointed out that the cubic nonlinear damping (denoted as the first type of nonlinear damping in this paper), i.e., \(f_{\mathrm{d}}^{\mathrm{I}} \propto \dot{r}^{3}\) (\(f_{\mathrm{d}}^{\mathrm{I}}\) is the damping force and \(\dot{r}\) denotes the relative velocity), can suppress the resonance amplitude while keep the force transmissibility almost unchanged at low or high frequencies for a single-degree-of-freedom (SDOF) isolator. This concept was also extended to the study of multi-degree-of-freedom (MDOF) isolation problems by Peng [6] and Lang [7]. Another type of nonlinear damping of similar beneficial effects is also cubic, whose force is a function of both displacement and velocity [8, 9] (referred as the second type of nonlinear damping in the following sections), i.e., \(f_{\mathrm{d}}^{\mathrm{II}} \propto r^{2}\dot{r}(f_{\mathrm{d}}^{\mathrm{II}} \) is the damping force, r and \(\dot{r}\) denotes the displacement and velocity, respectively) or a more general form of velocity-displacement-dependent nonlinear damping force described in Ref. [10]. Performance comparisons of these two types of nonlinear damping in free vibrations and forced vibrations can be found in Refs. [11,12,13]. Based on the results obtained with the harmonic balance method, Tang and Brennan [12] pointed out that the force transmissibility of both types of pure nonlinear damped isolators (\(f_{\mathrm{d}}^{\mathrm{I}} \) and \(f_{\mathrm{d}}^{\mathrm{II}} )\) can achieve 40dB/decade roll off at high frequencies and provide high damping effects during resonance. Nevertheless, for the displacement transmissibility under base excitations, the isolator with second type of nonlinear damping \(f_{\mathrm{d}}^{\mathrm{II}} \) still has 20dB/decade roll off, while the isolator owning first type of nonlinear damping \(f_{\mathrm{d}}^{\mathrm{I}} \) has nearly no isolation effects at high frequencies. These two types of nonlinear damping were also analytically compared by Xiao [13] with the nonlinear output frequency response concept considering higher order harmonics and reached the same conclusion.

As a matter of fact, the power order of the damping force with respect to relative velocity of a viscous damper can only be physically realized within the range from 0.2 to 1.95, i.e., \(f_{\mathrm{d}} ={\dot{r}}^{n}(n\in \left[ {0.2,1.95} \right] )\) [14, 15], which gives significant limitations to the implementation of both types of nonlinear dampers (\(f_{\mathrm{d}}^{\mathrm{I}} \) and \(f_{\mathrm{d}}^{\mathrm{II}} )\) by employing passive elements. Thus, Laalej [16] had to develop an active control strategy to generate the first type of cubic damping (\(f_{\mathrm{d}}^{\mathrm{I}} )\) and experimentally studied the nonlinear damping effects since no passive damping element has been reported to own this type of nonlinearity (\(f_{\mathrm{d}}^{\mathrm{I}}\)) up till now. Recently, Tang and Brennan [11, 12] made a progress by proposing a mechanism involving a horizontal linear damper orthogonal to a linear spring. Due to the unique geometrical arrangement of this damper, the second type of nonlinear damping (\(f_{\mathrm{d}}^{\mathrm{II}} \)) can be realized under low amplitude excitations. This geometrically nonlinear isolator was further extended to a more generalized model where the original horizontal linear damper is replaced with a velocity-nth power damper [17]. Interested readers can refer to a more comprehensive review summarized by Liu [18].

As been discussed above, in order to simultaneously meet the requirements of low resonance amplitude and good isolation performance at high-frequency range, these scholars [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] studied the lightly damped or even no damped linear isolators (already have good isolation efficiency at high frequencies) and added nonlinear damping elements to improve their poor resonance performances. While in this paper, we develop another novel way by presenting a sufficient damped isolator (naturally owns low resonance amplitude) and employ a nonlinear spring to reduce its vibration transmissibility at high frequencies without deteriorating its resonance performance. More specifically, we study the model of a linear spring in parallel with a nonlinear supported damper. This model is often known as the Zener model [23], and the nonlinear supported damper in this model consists of a linear damper and an intentional designed nonlinear spring, which is referred to as the secondary spring [24].

It is of advantage to use the proposed nonlinear isolator: First, this isolator consists of nonlinear stiffness elements instead of nonlinear dampers. It is known that there exist plenty more passive nonlinear spring mechanisms, such as variable coil diameter spring, thin-walled rubber cylinder, tensioned string, etc, and much wider range of practically possible nonlinear coefficients with design examples and criteria [18,19,20,21,22] compared to cubic nonlinear damping in the form of \(f_{\mathrm{d}}^{\mathrm{I}} \) or \(f_{\mathrm{d}}^{\mathrm{II}} \). Second, both force and displacement transmissibility of the presented nonlinear isolator (with nonlinear secondary spring) decreases at the rate of 40dB/decade at high frequencies, which owns better isolation performance than that of current nonlinear damping model of \(f_{\mathrm{d}}^{\mathrm{I}} \) (40dB/decade roll off for force transmissibility and no isolation effects in terms of displacement transmissibility) and \(f_{\mathrm{d}}^{\mathrm{II}} \) (40dB/decade roll off for force transmissibility and 20dB/decade roll off with respect to displacement transmissibility). Third, the present isolator is developed from a sufficient damped linear Zener model; thus, the higher harmonics can be greatly suppressed by the inherent linear damping, while for previous lightly linear damped or no linear damping isolators with cubic damping (\(f_{\mathrm{d}}^{\mathrm{I}} \) or \(f_{\mathrm{d}}^{\mathrm{II}} )\), the higher harmonics introduced by the isolators may have considerable effects, especially around resonances.

Fig. 1
figure 1

SDOF system with nonlinear supported damper in parallel with a linear spring subjected to force excitation

Full size image

The paper is organized as follows: In Sect. 2 the new Zener model with nonlinear secondary spring will be presented with analytical study in terms of its force and displacement transmissibility. Section 3 gives numerical study and parameter discussions to validate the analytical predictions and finally comes the conclusions described in Sect. 4.

2 Force and displacement transmissibility

2.1 Description of nonlinear Zener model

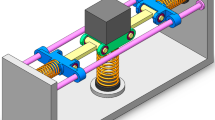
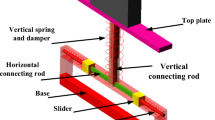
The nonlinear isolator considered in this paper is shown in Figs. 1 and 2 for the study of force excitation and base excitation, respectively. This type of isolators are often called viscous relaxation system [23], and its dynamic model is often referred as the Zener model [24]. The spring connected to the damper and the spring in parallel with the damper are called the secondary spring and the primary spring [24], respectively. Properties of the Zener model with linear springs, which is named as the linear Zener model here, have been extensively studied in Refs. [23] and [24]. In this paper, the nonlinearity of the secondary spring is considered and studied. Consequently, the model with a nonlinear secondary spring is called the nonlinear Zener model in the present paper for emphasizing this feature.

Fig. 2
figure 2

SDOF system with nonlinear supported damper in parallel with a linear spring subjected to base excitation

Full size image

As depicted in Figs. 1 and 2, the system consists of a payload mass m, a primary linear spring k, a linear viscous damper c and a cubic nonlinear secondary spring with its force \(f_{\mathrm{nl}} \) denoted by

$$\begin{aligned} f_{\mathrm{nl}} =k_{\mathrm{l}} r+k_{\mathrm{nl}} r^{3} \end{aligned}$$
(1)

where \(k_{\mathrm{l}} \) denotes the linear stiffness of the nonlinear spring and \(k_{\mathrm{nl}} \) denotes the coefficient of its cubic stiffness term. r denotes the relative motion of the nonlinear secondary spring as depicted in Figs. 1 and 2, which can be written as

$$\begin{aligned} r=\left\{ {{\begin{array}{lll} {x_2 }&{} \quad {\hbox {under}}&{} {\hbox {force-excitation}} \\ {x_2 -x_{\mathrm{in}} }&{} \quad {\hbox {under}}&{} {\hbox {base-excitation}} \\ \end{array} }} \right. \end{aligned}$$
(2)

where \(x_2\) denotes the displacement at one end of the secondary spring and \(x_{\mathrm{in}}\) denotes the input of base excitations, as shown in Figs. 1 and 2.

As the isolator subjected to harmonic excitation and considered with sufficient linear damping (e.g., with a linear modal damping of 0.1–0.3), the primary harmonic term can be assumed to dominate its steady-state response [25,26,27], i.e.,

$$\begin{aligned} r\approx \hbox {Im}\left( {R\hbox {e}^{\mathrm{j}\varphi }} \right) \end{aligned}$$
(3)

where R denotes the complex response of the nonlinear secondary spring, \(\varphi \) denotes its generic angle and \(\hbox {j}\) is the imaginary unit.

Thus, according to the principle of equivalent linearization method [28, 29] or describing functions [30], the nonlinear force defined by Eq. (1) can be linearized as

$$\begin{aligned} f_{\mathrm{nl}} =k_{\mathrm{eq}} r \end{aligned}$$
(4)

where

$$\begin{aligned} k_{\mathrm{eq}} =k_{\mathrm{l}} +\frac{3}{4}k_{\mathrm{nl}} \left| R \right| ^{2} \end{aligned}$$
(5)

and \(\left| R \right| \) denotes the amplitude of R.

2.2 Force transmissibility under force excitations

As shown in Fig. 1, the force excitation is denoted by

$$\begin{aligned} f_{\mathrm{in}} \left( t \right) ={\bar{f}}_{\mathrm{in}} \sin \left( {\omega t} \right) \end{aligned}$$
(6)

where \({\bar{f}}_{\mathrm{in}}\) denotes the amplitude of the force excitation and the dynamic equation of the system can be written as

$$\begin{aligned} \left\{ {{\begin{array}{l} {m\ddot{x}_1 +c\left( {\dot{x}_1 -\dot{x}_2 } \right) +kx_1 ={\bar{f}}_{\mathrm{in}} \sin \left( {\omega t} \right) } \\ {c\left( {\dot{x}_1 -\dot{x}_2 } \right) =f_{\mathrm{nl}} \left( {x_2 } \right) } \\ \end{array} }} \right. \end{aligned}$$
(7)

where \(x_1 \), \({\dot{x}}_1\), and \({\ddot{x}}_1 \) denote the displacement, velocity and acceleration of the sprung mass, respectively. \({\dot{x}}_2 \) denotes the velocity of \(x_2\).

According to Fig. 1, the force transferred to the base can be denoted by

$$\begin{aligned} f_{\mathrm{out}} =kx_1 +c\left( {\dot{x}_1 -\dot{x}_2 } \right) \end{aligned}$$
(8)

Introduce non-dimensional variables \(\omega _{0}^{2} =k/m\), \(\varOmega =\omega /{\omega _0 }\), \(\tau =\omega _0 t\), \({\hat{f}}_{\mathrm{in}} ={\bar{f}}_{\mathrm{in}} /k\), \(\zeta =c/{2\sqrt{km}}\) and \({\hat{f}}_{\mathrm{nl}} ={f_{\mathrm{nl}} }/k\), yielding

$$\begin{aligned} \left\{ {{\begin{array}{l} {x_1 ^{\prime \prime }+2\zeta \left( {x_1 ^{\prime }-x_2 ^{\prime }} \right) +x_1 ={\hat{f}}_{\mathrm{in}} \sin \left( {\varOmega \tau } \right) } \\ {2\zeta \left( {x_1 ^{\prime }-x_2 ^{\prime }} \right) ={\hat{f}}_{\mathrm{nl}} \left( {x_2 } \right) } \\ \end{array} }} \right. \end{aligned}$$
(9)

where \({{\bullet }}'\) denotes the derivative of the variable with respect to non-dimensional time.

Thus, the nonlinear equation of relative motion can be written in the frequency domain as

$$\begin{aligned} X_2 =\frac{\hbox {j}{} \textit{2}\zeta \varOmega }{-\hbox {j}{} \textit{2}\zeta \varOmega ^{3}-{\hat{k}}_{\mathrm{eq}_{\mathrm{f}}} \varOmega ^{2}+\hbox {j}{} \textit{2}\zeta \varOmega \left( {\hat{k}}_{\mathrm{eq}_{\mathrm{f}}} +1 \right) +{\hat{k}}_{\mathrm{eq}_{\mathrm{f}}} }{\hat{F}}_{\mathrm{in}} \end{aligned}$$
(10)

where \(X_2\) denotes the complex relative motion of the nonlinear secondary spring. \({\hat{F}}_{\mathrm{in}}\) denotes the complex amplitude of the force input \(f_{\mathrm{in}} \left( t \right) \). According to Eqs. (2) and (5), we also have

$$\begin{aligned} {\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} =\beta _{\mathrm{l}} +\frac{3}{4}\beta _{\mathrm{nl}} \left| {X_2 } \right| ^{2} \end{aligned}$$
(11)

where \(\beta _{\mathrm{l}}\) and \(\beta _{\mathrm{nl}}\) represent the non-dimensional linear and nonlinear coefficients of the secondary spring, respectively. They can be obtained by

$$\begin{aligned} \beta _{\mathrm{l}} ={k_{\mathrm{l}} }/k,\beta _{\mathrm{nl}} ={k_{\mathrm{nl}} }/k \end{aligned}$$
(12)

It should be noted that nonlinear equation of relative motion defined by Eq. (10) needs to be solved iteratively [8, 25,26,27,28,29,30] or inversely [31] to obtain the responses since \({\hat{k}}_{\mathrm{eq}_{\mathrm{f}}}\) is dependent on the responses \(X_2\), although it can be written in a form of ‘linear’ transfer function.

After solving Eq. (10), the force transmissibility can be calculated with

$$\begin{aligned} T_{\mathrm{f}} =\frac{\hbox {j}{} \textit{2}\zeta \varOmega \left( {\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} +1 \right) +{\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} }{-\hbox {j}{} \textit{2}\zeta \varOmega ^{3}-{\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} \varOmega ^{2}+\hbox {j}{} \textit{2}\zeta \varOmega \left( {\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} +1 \right) +{\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} } \end{aligned}$$
(13)

Before numerical simulation of the responses, we first present the analytical study of the isolator on its high-frequency transmissibility as well as resonance amplitude.

(a) High frequency performance

At high frequencies, the modulus of Eq. (10) becomes

$$\begin{aligned}&\left| {X_2 } \right| _{\varOmega>>1} \nonumber \\&\quad =\left| {\frac{\hbox {j}{} \textit{2}\zeta \varOmega }{-\hbox {j}{} \textit{2}\zeta \varOmega ^{3}-{\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} \varOmega ^{2}+\hbox {j}{} \textit{2}\zeta \varOmega \left( {\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} +1 \right) +{\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} }} \right| \nonumber \\&\qquad \times \left| {\hat{F}}_{\mathrm{in}} \right| \nonumber \\&\quad \approx \frac{\left| {\hat{F}}_{\mathrm{in}} \right| }{\varOmega ^{2}} \end{aligned}$$
(14)

thus the force transmissibility defined by Eq. (13) can be approximately calculated by

$$\begin{aligned} \left| {T_{\mathrm{f}} } \right| _{\varOmega>>1}\approx & {} \left| {\frac{\left( {\hat{k}}_{\mathrm{eq}_{\mathrm{f }}} +1 \right) }{\varOmega ^{2}}} \right| =\frac{\beta _{\mathrm{l}} +\frac{3}{4}\beta _{\mathrm{nl}} {\left| {\hat{F}}_{\mathrm{in}} \right| ^{2}}\Big /{\varOmega ^{4}}+1}{\varOmega ^{2}}\nonumber \\\approx & {} \frac{\beta _{\mathrm{l}} +1}{\varOmega ^{2}} \end{aligned}$$
(15)

For a conventional linear Zener model [23, 24],

$$\begin{aligned} \beta _{\mathrm{l}} \ne 0,\quad \beta _{\mathrm{nl}} =0 \end{aligned}$$
(16)

and the linear force transmissibility can be obtained as

$$\begin{aligned} \left| {T_{\mathrm{f}} } \right| _{\varOmega>>1}^{\mathrm{linear}} \approx \frac{\beta _{\mathrm{l}} +1}{\varOmega ^{2}} \end{aligned}$$
(17)

If only the pure cubic stiffness of the secondary spring is considered, there are

$$\begin{aligned} \beta _{\mathrm{l}} =0,\quad \beta _{\mathrm{nl}} \ne 0 \end{aligned}$$
(18)

then the force transmissibility of the nonlinear Zener model will be

$$\begin{aligned} \left| {T_{\mathrm{f}} } \right| _{\varOmega>>1}^{\mathrm{nonlinear}} \approx \frac{1}{\varOmega ^{2}} \end{aligned}$$
(19)

As can be seen from Eqs. (17) and (19), the force transmissibility of both linear and nonlinear Zener model at high frequencies is independent of the damping, and decreases at a rate of 40dB/decade, which is actually one merit of the isolators features with the Zener model. By comparing Eqs. (17) and (19), it is also obvious that employing pure nonlinear stiffness in the secondary spring will reduce the transmissibility by a factor of \(\beta _{\mathrm{l}} +1\) in high frequencies with respect to the linear Zener model, and obtaining the same high-frequency transmissibility of an isolator with rigidly connected pure cubic nonlinear damper (\(f_{\mathrm{d}}^{\mathrm{I}}\) and \(f_{\mathrm{d}}^{\mathrm{II}}\)) [12].

(b) Resonance performance

It is already known that the resonance frequency of the linear Zener mode will change with the non-dimensional damping parameter \(\zeta \) [24]. In this paper, the damping coefficient is not assumed too high (\(\zeta \le 0.4\)), and thus the resonance will occur near \(\varOmega =1\).

For the linear Zener model (\(\beta _{\mathrm{l}} \ne 0,\beta _{\mathrm{nl}} =0\)),

$$\begin{aligned} \left| {X_2 } \right| _{\varOmega =1}^{\mathrm{linear}} =\frac{1}{\beta _{\mathrm{l}} }\left| {\hat{F}}_{\mathrm{in}} \right| \end{aligned}$$
(20)

So that

$$\begin{aligned} \left| {T_{\mathrm{f}} } \right| _{\varOmega =1}^{\mathrm{linear}}= & {} \left| {1+\frac{1}{\beta _{\mathrm{l}} }-\frac{j}{2\zeta }} \right| \nonumber \\= & {} \sqrt{\left( {1+\frac{1}{\beta _{\mathrm{l}} }} \right) ^{2}+\left( {\frac{1}{2\zeta }} \right) ^{2}} \end{aligned}$$
(21)

Similarly, for the nonlinear Zener model with pure cubic stiffness of the secondary spring (\(\beta _{\mathrm{l}} =0,\beta _{\mathrm{nl}} \ne 0\)),

$$\begin{aligned} \left| {X_2 } \right| _{\varOmega =1}^{\mathrm{nonlinear}} =\root 3 \of {{4\left| {\hat{F}}_{\mathrm{in}} \right| }/{3\beta _{\mathrm{nl}} }} \end{aligned}$$
(22)

and

$$\begin{aligned}&\left| {T_{\mathrm{f}}} \right| _{\varOmega =1}^{\mathrm{nonlinear}} =\left| 1+\frac{1}{\frac{3}{4}\beta _{\mathrm{nl}} \left( 4\left| {\hat{f}}_{\mathrm{in}} \right| \Big /{3\beta _{\mathrm{nl}}} \right) ^{2/3}}-\frac{j}{2\zeta } \right| \nonumber \\&\quad =\sqrt{\left[ 1+\frac{1}{\root 3 \of {3}\left| {\hat{f}}_{\mathrm{in}} \right| ^{2}\beta _{\mathrm{nl}}\Big /4} \right] ^{2}+\left( {1/{2\zeta }} \right) ^{2}} \end{aligned}$$
(23)

The resonance amplitude of the nonlinear Zener model will be lower or equal to that of the linear Zener model provided that

$$\begin{aligned} \root 3 \of {3\left| {{\hat{f}}_{\mathrm{in}}} \right| ^{2}\beta _{\mathrm{nl}} \Big /4}\ge \beta _{\mathrm{l}} \end{aligned}$$
(24)

Equation (24) is a nonlinear equation related to the input force \({\hat{f}}_{\mathrm{in}}\) and isolator parameters (\(\beta _{\mathrm{l}}\) and \(\beta _{\mathrm{nl}}\)). If it is satisfied, one will have

$$\begin{aligned} \sqrt{1+\left( {1/{2\zeta }} \right) ^{2}}\le \left| {T_{\mathrm{f}} } \right| _{\varOmega =1}^{\mathrm{nonlinear}} \le \left| {T_{\mathrm{f}} } \right| _{\varOmega =1}^{\mathrm{linear}} \end{aligned}$$
(25)

As indicated by Eq. (25), although the resonance amplitudes of both linear and nonlinear Zener model are larger than that of the isolator with linear rigidly connected damper of the same damping value \(\zeta \), the isolator featured with nonlinear Zener model owns lower resonance amplitude compared to that of the linear Zener model if it satisfies Eq. (24).

(c) Jump avoidance

In practical applications, jumps of the transmissibility curves should be avoided. According to Eqs. (10) and (11), we can obtain the implicit amplitude-frequency equation

$$\begin{aligned} C_6 \left| {x_2 } \right| ^{6}+C_4 \left| {x_2 } \right| ^{4}+C_2 \left| {x_2 } \right| ^{2}+C_0 =0 \end{aligned}$$
(26)

where

$$\begin{aligned} {C_6 }= & {} {\frac{9}{16}\beta _{\mathrm{nl}}^2 \left[ {\left( {\varOmega ^{2}{-}1} \right) ^{2}{+}4\zeta ^{2}\varOmega ^{2}} \right] }\nonumber \\ {C_4 }= & {} {\frac{3}{2}\beta _{\mathrm{nl}} \beta _{\mathrm{l}} \left( {\varOmega ^{2}{-}1} \right) ^{2}{-}6\beta _{\mathrm{nl}} \zeta ^{2}\varOmega ^{2}\left( {\varOmega ^{2}{-}\beta _{\mathrm{l}} {-}1} \right) } \nonumber \\ {C_2 }= & {} {4\zeta ^{2}\varOmega ^{2}\left( {\varOmega ^{2}{-}\beta _{\mathrm{l}} {-}1} \right) ^{2}{+}\beta _{\mathrm{l}}^2 \left( {\varOmega ^{2}{-}1} \right) ^{2}} \nonumber \\ {C_0 }= & {} {-4\zeta ^{2}\varOmega ^{2}\left| {\hat{F}}_{\mathrm{in}} \right| ^{2}} \end{aligned}$$
(27)

Next, the critical equation [8] corresponding to a vertical slope can be established by \({\partial \varOmega }/{\partial \left| {X_2 } \right| }=0\) to evaluate the jump condition of this isolator, where the jump zone and non-jump zone are divided by the solution curve of this critical equation, i.e.,

$$\begin{aligned} 6C_6 \left| {x_2 } \right| ^{5}+4C_4 \left| {x_2 } \right| ^{3}+2C_2 \left| {x_2 } \right| =0 \end{aligned}$$
(28)

where \(C_6 \), \(C_4 \), and \(C_2 \) are the coefficients defined by Eq. (27).

Thus, jump phenomenon can be avoided [8] if the response curve of the isolator under force excitations has just one or none point that satisfies Eq. (28).

(d) Brief summary of force transmissibility analysis

In Sect. 2.2, the force transmissibility of the nonlinear Zener model around its resonance and at high frequencies is discussed analytically. It is shown that choosing pure cubic stiffness as the type of secondary spring can have better force transmissibility than its corresponding linear Zener model at high frequencies. In addition, if its nonlinear parameters satisfy Eq. (24), the nonlinear Zener model will even has lower resonance amplitude with respect to the linear one. Thus, a nonlinear secondary spring with parameters satisfying Eq. (24) can help the Zener model to achieve an ideal improvement on the force transmissibility, i.e., the isolation performance at high frequencies will be enhanced, and meanwhile the resonance amplitude can be maintained or even suppressed. Thereafter, the jump avoidance criteria is also derived using its critical equation, which should be satisfied during practical applications.

2.3 Displacement transmissibility under base excitations

As depicted in Fig. 2, the base displacement excitation can be expressed by

$$\begin{aligned} x_{\mathrm{in}} \left( t \right) ={\bar{x}}_{\mathrm{in}} \sin \left( {\omega t} \right) \end{aligned}$$
(29)

where \({\bar{x}}_{\mathrm{in}}\) denotes the amplitude of the base excitations.

The governing equation of the system is

$$\begin{aligned} \left\{ {{\begin{array}{l} {m\ddot{x}_1 +c\left( {\dot{x}_1 -\dot{x}_2 } \right) +k\left( {x_1 -x_{\mathrm{in}} } \right) =0} \\ {c\left( {\dot{x}_1 -\dot{x}_2 } \right) =f_{\mathrm{nl}} \left( {x_2 -x_{\mathrm{in}} } \right) } \\ \end{array} }} \right. \end{aligned}$$
(30)

Once again, introducing the non-dimensional variables \(\omega _{0}^{2} =k/m\), \(\varOmega =\omega /{\omega _0 }\), \(\tau =\omega _0 t\), \(\zeta =c/{2\sqrt{km}}\) and \({\hat{f}}_{\mathrm{nl}} ={\hat{f}}_{\mathrm{nl}}/k\), there is

$$\begin{aligned} \left\{ {{\begin{array}{l} {x_1 ^{\prime \prime }+2\zeta \left( {x_1 ^{\prime }-x_2 ^{\prime }} \right) +\left( {x_1 -x_{\mathrm{in}} } \right) =0} \\ {2\zeta \left( {x_1 ^{\prime }-x_2 ^{\prime }} \right) ={\hat{f}}_{\mathrm{nl}} \left( {x_2 -x_{\mathrm{in}} } \right) } \\ \end{array} }} \right. \end{aligned}$$
(31)

where \({{\bullet }}'\) denotes the derivative of the variable with respect to non-dimensional time.

With the relative motion of the nonlinear secondary spring defined by Eq. (2), the complex response of the relative motion of the nonlinear secondary spring can be written as

$$\begin{aligned} R=\frac{\hbox {j}{} \textit{2}\zeta \varOmega ^{3}}{-\hbox {j}{} \textit{2}\zeta \varOmega ^{3}-{\hat{k}}_{\mathrm{eq}_\mathrm{b }} \varOmega ^{2}+\hbox {j}{} \textit{2}\zeta \left( {\hat{k}}_{\mathrm{eq}_\mathrm{b }} +1 \right) \varOmega +{\hat{k}}_{\mathrm{eq}_\mathrm{b }} }X_{\mathrm{in}} \end{aligned}$$
(32)

where \(X_{\mathrm{in}}\) denotes the complex amplitude of the base excitation, R denotes the complex response of the nonlinear secondary spring . The \({\hat{k}}_{\mathrm{eq}_\mathrm{b}}\) can be obtained according to Eqs. (2) and (5) by

$$\begin{aligned} {\hat{k}}_{\mathrm{eq}_\mathrm{b }} =\beta _{\mathrm{l}} +\frac{3}{4}\beta _{\mathrm{nl}} \left| R \right| ^{2} \end{aligned}$$
(33)

where \(\beta _{\mathrm{l}}\) and \(\beta _{\mathrm{nl}}\) are also defined by Eq. (12), representing the non-dimensional linear and nonlinear coefficients of the secondary spring, respectively.

Similar to Eqs. (10), (32) is also a nonlinear equation that needs to be solved iteratively [30] or inversely [31] due to its inherent nonlinear feature. After solving it, the displacement transmissibility can be obtained by

$$\begin{aligned} T_{\mathrm{d}} =\frac{\hbox {j}{} \textit{2}\zeta \left( {\hat{k}}_{\mathrm{eq}_\mathrm{b }} +1 \right) \varOmega +{\hat{k}}_{\mathrm{eq}_\mathrm{b }} }{-\hbox {j}{} \textit{2}\zeta \varOmega ^{3}-{\hat{k}}_{\mathrm{eq}_\mathrm{b }} \varOmega ^{2}+\hbox {j}{} \textit{2}\zeta \left( {\hat{k}}_{\mathrm{eq}_\mathrm{b }} +1 \right) \varOmega +{\hat{k}}_{\mathrm{eq}_\mathrm{b }} } \end{aligned}$$
(34)

Again, we analytically study its isolation performance in terms of its transmissibility at high frequencies and resonance amplitude.

(a) High frequency performance

At high frequencies and according to Eq. (32), one have

$$\begin{aligned} \left| R \right| _{\varOmega>>1} \approx \left| {X_{\mathrm{in}} } \right| \end{aligned}$$
(35)

Thus, the modulus of displacement transmissibility becomes

$$\begin{aligned}&\left| {T_{\mathrm{d}} } \right| _{\varOmega>>1}\nonumber \\&\quad \approx \left| {\frac{\hbox {j}{} \textit{2}\zeta \left( {\hat{k}}_{\mathrm{eq}_\mathrm{b }} +1 \right) \varOmega +{\hat{k}}_{\mathrm{eq}_\mathrm{b }} }{-\hbox {j}{} \textit{2}\zeta \varOmega ^{3}-{\hat{k}}_{\mathrm{eq}_\mathrm{b }} \varOmega ^{2}+\hbox {j}{} \textit{2}\zeta \left( {\hat{k}}_{\mathrm{eq}_\mathrm{b }} +1 \right) \varOmega +{\hat{k}}_{\mathrm{eq}_\mathrm{b }} }} \right| \nonumber \\&\quad \approx \frac{\beta _{\mathrm{l}} +\frac{3}{4}\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}+1}{\varOmega ^{2}} \end{aligned}$$
(36)

For a conventional linear Zener model (\(\beta _{\mathrm{l}} \ne 0,\beta _{\mathrm{nl}} =0\)), we have

$$\begin{aligned} \left| {T_{d} } \right| _{\varOmega>>1}^{\mathrm{linear}} \approx \frac{\beta _{\mathrm{l}} +1}{\varOmega ^{2}} \end{aligned}$$
(37)

If the secondary spring is considered as pure cubic stiffness (\(\beta _{\mathrm{l}} =0,\beta _{\mathrm{nl}} \ne 0\)), the displacement transmissibility of the nonlinear Zener model will be

$$\begin{aligned} \left| {T_{{d}} } \right| _{\varOmega>>1}^{\mathrm{nonlinear}} \approx \frac{\frac{3}{4}\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}+1}{\varOmega ^{2}} \end{aligned}$$
(38)

The displacement transmissibility of both linear and nonlinear Zener model at high frequencies decays at the rate of 40dB/decade, whereas it is only 20dB/decade for a traditional linear isolator with rigidly connected linear damper and the rigidly connected nonlinear damper with the second type of cubic damping (\(f_{\mathrm{d}}^{\mathrm{II}} \propto x^{2}\dot{x}\)) discussed in Refs. [12, 13]. It should also be noted that the first type of cubic damping \(f_{\mathrm{d}}^{\mathrm{I}} \propto \dot{x}^{3}\) offers on isolation effects at very high frequencies [12] under base excitations. From this point of view, both the linear and nonlinear Zener model have excellent isolation performance under base excitations at high frequencies.

In addition, provided that

$$\begin{aligned} \frac{3}{4}\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}\le \beta _{\mathrm{l}} \end{aligned}$$
(39)

The nonlinear Zener model with a pure cubic stiffness secondary spring will have better high-frequency isolation efficiency than the linear Zener model.

(b) Resonance performance

In this section, it is also assumed that the damping coefficient is not too high (\(\zeta \le 0.4\)) and the resonance occurs near \(\varOmega =1\).

For a linear Zener model (\(\beta _{\mathrm{l}} \ne 0,\beta _{\mathrm{nl}} =0\)),

$$\begin{aligned} \left| R \right| _{\varOmega =1}^{\mathrm{linear}} =\left| {\frac{X_{\mathrm{in}} }{\beta _{\mathrm{l}} }} \right| \end{aligned}$$
(40)

So that

$$\begin{aligned} \left| {T_{\mathrm{d}} } \right| _{\varOmega \hbox {=}1}^{\mathrm{linear}} =\sqrt{\left( {1+\frac{1}{\beta _{\mathrm{l}} }} \right) ^{2}+\left( {\frac{1}{2\zeta }} \right) ^{2}} \end{aligned}$$
(41)

For a nonlinear Zener model with a pure cubic stiffness secondary spring (\(\beta _{\mathrm{l}} =0,\beta _{\mathrm{nl}} \ne 0\)),

$$\begin{aligned} \left| R \right| _{\varOmega =1}^{\mathrm{nonlinear}} =\root 3 \of {{4\left| {X_{\mathrm{in}} } \right| }/{3\beta _{\mathrm{nl}} }} \end{aligned}$$
(42)

The nonlinear displacement transmissibility can be written as

$$\begin{aligned}&\left| {T_{\mathrm{d}} } \right| _{\varOmega =1}^{\mathrm{nonlinear}} \nonumber \\&\quad =\left| {1+\frac{1}{\frac{3}{4}\beta _{\mathrm{nl}} \left( {{4\left| {X_{\mathrm{in}} } \right| }/{3\beta _{\mathrm{nl}} }} \right) ^{2/3}}-\frac{j}{2\zeta }} \right| \nonumber \\&\quad =\sqrt{\left[ {1+\frac{1}{\root 3 \of {{3\left| {X_{\mathrm{in}} } \right| ^{2}\beta _{\mathrm{nl}} }/4}}} \right] ^{2}+\left( {1/{2\zeta }} \right) ^{2}} \end{aligned}$$
(43)

By letting

$$\begin{aligned} \root 3 \of {{3\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}}/4}\ge \beta _{\mathrm{l}} \end{aligned}$$
(44)

one can have

$$\begin{aligned} \sqrt{1+\left( {1/{2\zeta }} \right) ^{2}}\le \left| {T_{\mathrm{d}} } \right| _{\varOmega =1}^{\mathrm{nonlinear}} \le \left| {T_{\mathrm{d}} } \right| _{\varOmega =1}^{\mathrm{linear}} \end{aligned}$$
(45)

Similar to the force transmissibility, the peak value of the displacement transmissibility of the linear or nonlinear Zener model will be slightly larger than that of the isolator with linear rigidly connected damper at the same damping level of \(\zeta \). Including nonlinear secondary spring in the Zener model, with its parameters satisfying Eq. (44), the resonance amplitude will be suppressed compared to linear Zener model and closer to that of the isolator with linear rigidly connected damper.

Fig. 3
figure 3

Relations between the resonance amplitude and the nonlinear coefficients at different damping levels

Full size image

Thus, by employing a nonlinear secondary spring with parameters satisfying Eqs. (39) and (44) simultaneously, an ideal improvement of the displacement transmissibility of the Zener model can be achieved, i.e., satisfying

$$\begin{aligned} \beta _{\mathrm{l}} \le \frac{3}{4}\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}\le \root 3 \of {\beta _{\mathrm{l}} } \end{aligned}$$
(46)

Equation (46) indicates that Eqs. (39) and (44) can only be simultaneously satisfied when \(0\le \beta _{\mathrm{l}} \le 1\). As \(\beta _{\mathrm{l}} >1\), the effects of nonlinearity on the resonance amplitude \(\left| {T_{\mathrm{d}} } \right| _{\varOmega =1}^{\mathrm{nonlinear}} \) is marginal when \({3\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}}/4\ge 1\). As depicted in Fig. 3, when \(1\le \root 3 \of {{3\beta _{\mathrm{nl}} \left| {X_{\mathrm{in}} } \right| ^{2}}/4}<\beta _{\mathrm{l}} \), the nonlinear secondary spring will introduce a small increase in the resonance amplitude, while according to Eq. (39), the high-frequency transmissibility will be significantly reduced. That is to say, when \(\beta _{\mathrm{l}} >1\), the displacement transmissibility at high frequencies can still be substantially reduced at the cost of only a small increase of the resonance amplitude by replacing the linear secondary spring with a nonlinear one. This conclusion will be demonstrated with numerical examples in the next section.

(c) Jump avoidance

Similar to the analysis in Sect. 2.2, the implicit amplitude-frequency equation of Eq. (32) can be obtained as

$$\begin{aligned} D_6 \left| R \right| ^{6}+D_4 \left| R \right| ^{4}+D_2 \left| R \right| ^{2}+D_0 =0 \end{aligned}$$
(47)

where

$$\begin{aligned} {D_6 }= & {} {\frac{9}{16}\beta _{\mathrm{nl}}^2 \left[ {\left( {\varOmega ^{2}{-}1} \right) ^{2}{+}4\zeta ^{2}\varOmega ^{2}} \right] }\nonumber \\ {D_4 }= & {} {\frac{3}{2}\beta _{\mathrm{nl}} \beta _{\mathrm{l}} \left( {\varOmega ^{2}{-}1} \right) ^{2}{-}6\beta _{\mathrm{nl}} \zeta ^{2}\varOmega ^{2}\left( {\varOmega ^{2}{-}\beta _{\mathrm{l}} {-}1} \right) } \nonumber \\ {D_2 }= & {} {4\zeta ^{2}\varOmega ^{2}\left( {\varOmega ^{2}{-}\beta _{\mathrm{l}} -1} \right) ^{2}{+}\beta _{\mathrm{l}}^2 \left( {\varOmega ^{2}-1} \right) ^{2}} \nonumber \\ {D_0 }= & {} {-4\zeta ^{2}\varOmega ^{6}\left| {X_{\mathrm{in}}} \right| ^{2}} \end{aligned}$$
(48)

According to the critical equation [8] denoted by \({\partial \varOmega }/{\partial \left| R \right| }=0\), one obtain

$$\begin{aligned} 6D_6 \left| R \right| ^{5}+4D_4 \left| R \right| ^{3}+2D_2 \left| R \right| =0 \end{aligned}$$
(49)

where \(D_6 \), \(D_4 \),and \(D_2 \) are defined by Eq. (48)

Similarly, jump phenomenon can also be avoided [8] if the response curve of the isolator under base excitations has just one or none point that satisfies Eq. (49).

(d) Brief summary of displacement transmissibility analysis

In Sect. 2.3, the displacement transmissibility at high frequencies and around resonance is discussed. It is shown that the displacement transmissibility of both the linear and nonlinear Zener model decreases at the rate of 40dB/decade at high frequencies, which indicate better isolation performance than the isolator with rigidly connected linear damper (20 dB/decade roll off) or even the rigidly connected nonlinear damper (no isolation effects for \(f_{\mathrm{d}}^{\mathrm{I}} \) and 20 dB/decade roll off for \(f_{\mathrm{d}}^{\mathrm{II}} \) [12, 13], respectively).

When compared to linear Zener model, the pure nonlinear secondary spring in Zener model can achieve an ideal improvement (reducing the transmissibility at high frequencies as well as suppressing the resonance amplitude) when \(0\le \beta _{\mathrm{l}} \le 1\), or substantially reduce the transmissibility at high frequencies with only a small increase of the resonance amplitude if \(\beta _{\mathrm{l}} >1\).

3 Numerical examples and discussions

The force transmissibility as the isolator subjected to the force excitations and displacement transmissibility as the isolator subjected to the base excitations will be numerically studied in this section. For each input scenario, the transmissibility curve of the isolator was first solved in the frequency domain with Newton-Raphaen iterations [25,26,27,28] and plotted as lines in the following figures. Then, direct time integration was also performed to validate the frequency domain results, where the time history responses of the nonlinear Zener model were obtained by integrating the original time domain equation (Eqs. 9 and 31, respectively) with Runge-Kutta algorithm in MATLAB. The time step was chosen as a fixed step dividing each driven cycle into 100 steps, the total integration time was set as 8000 cycles and the last 800 cycle steady-state data were used in fast Fourier transform (FFT) to obtain the primary, third and fifth harmonic term of the responses. In addition, the amplitudes of each harmonic term obtained from direct time integration are plotted as discrete markers in the same figure of the frequency domain results for the purpose of comparison.

3.1 Force transmissibility under force excitations

As shown in Fig. 1, the parameters of original linear Zener model was chosen as \(\zeta =0.1\), \(\beta _{\mathrm{l}} =1\), \(\beta _{\mathrm{nl}} =0\) and the amplitude of input force was considered as \({\hat{F}} _{\mathrm{in}} =0.4\).

Here, only the secondary spring was changed from linear to nonlinear while other parameters kept unchanged, i.e., consider \(\zeta =0.1\), \(\beta _{\mathrm{l}} =0\) for the design of nonlinear Zener model. According to Eq. (24), in order to obtain better vibration isolation performance at high frequencies, the nonlinear coefficient needs to satisfy \(\beta _{\mathrm{nl}} \ge {25}/3\). In this example, we chose \(\beta _{\mathrm{nl}} ={25}/3\), which means the nonlinear Zener model owns the same resonance amplitude and achieves maximum percentage enhancement in transmissibility performance at high frequencies compared to the linear Zener model.

Apart from the linear Zener model and nonlinear Zener model, the linear rigid connected damper model with the same damping level was also included for the purpose of comparison, and it was obtained by letting \(\beta _{\mathrm{l}} \rightarrow +\infty \), \(\beta _{\mathrm{nl}} =0\) and \(\zeta =0.1\).

The transmissibility of linear Zener model and its corresponding nonlinear Zener model compared in terms of its high-frequency performance and resonance amplitude are shown in Fig. 4, in which multiple harmonic terms obtained from direct numerical integration are also plotted as markers. As depicted in Fig. 4, good agreement is observed between analytical predictions with frequency domain solutions and primary harmonic term from time domain integration. It is also evident that the response amplitude of higher order harmonics is at least 20dB less than that of the primary harmonic term.

Fig. 4
figure 4

The force transmissibility as the isolator subject to force excitations. Dashed line: linear rigid connected damper (\(\beta _{\mathrm{l}} \rightarrow +\infty \), \(\beta _{\mathrm{nl}} =0\) and \(\zeta =0.1\)); Short dashed line: linear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =1\) and \(\beta _{\mathrm{nl}} =0\)); Solid line: nonlinear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =0\), \(\beta _{\mathrm{nl}} ={25}/3\)). The markers denoted by each harmonic term were obtained from direct time integration of the nonlinear Zener model. a wide frequency range, b around resonance

Full size image

As can be seen from the comparison in Fig. 4, the force transmissibility of the linear and nonlinear Zener model at high frequencies is better than that of the isolator with linear rigidly connected damper. At high frequencies, the nonlinear Zener model isolator has even better performance than the linear Zener model, which is in agreement with the analytical predictions in Sect. 2.2. It should be noted that the high-frequency transmissibility can also be improved by reducing \(\beta _{\mathrm{l}} \) to a very small value in a linear Zener model isolator. However, this will lead to an unacceptable increase of the resonance amplitude. It is clearly shown in Fig. 4b that the nonlinear Zener model with a pure cubic stiffness secondary spring (\(\beta _{\mathrm{l}} =0\), \(\beta _{\mathrm{nl}} ={25}/3\)) can behave similarly and have the same resonance amplitude as a linear Zener model isolator (\(\beta _{\mathrm{l}} =1\), \(\beta _{\mathrm{nl}} =0\)) in the low frequency range (\(\varOmega \le 1.8\)), and the transmissibility will drop below that of the linear Zener model in the high frequency range(\(\varOmega \ge 2.5\)). In this way, the nonlinear secondary spring can significantly improve the force transmissibility performance of the isolator, especially its high-frequency isolation efficiency.

3.2 Displacement transmissibility under base excitations

The displacement transmissibility is also studied with the non-dimensional damping \(\zeta =0.1\) and base excitation level \(x_{\mathrm{in}} =0.4\). Consider two groups of isolators according to the range of \(\beta _{\mathrm{l}} \) in linear Zener model, i.e., \(\beta _{\mathrm{l}} \ge 1\) and \(0\le \beta _{\mathrm{l}} \le 1\), during the numerical study.

  1. (a)

    \(\beta _{\mathrm{l}} \ge 1\), i.e., the stiffness of the secondary spring is larger than that of the primary spring in the linear Zener model

The first group contains isolators with a linear rigidly connected damper (\(\beta _{\mathrm{l}} \rightarrow +\infty \), \(\beta _{\mathrm{nl}} =0\) and \(\zeta =0.1\)), a linear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =5\), \(\beta _{\mathrm{nl}} =0\)) and a nonlinear Zener model that needs to be designed. Since \(\beta _{\mathrm{l}} =5\ge 1\) was assumed for the linear Zener model, we cannot find a nonlinear Zener model with a secondary spring of pure cubic stiffness, which has both lower resonance amplitude and better high frequency transmissibility than that of the linear Zener model according to Eq. (46). Here, we chose a set of parameters \(\zeta =0.1\), \(\beta _{\mathrm{l}} =0\) and \(\beta _{\mathrm{nl}} ={25}/3\) for the nonlinear Zener model, which only satisfying Eq. (39). Thus, the resonance amplitude increases from 5.14 to 5.85, while the transmissibility at \(\varOmega =100\) reduces from 6e−4 to 2e−4, as shown in Fig. 5. From the comparison of this group, it is demonstrated that a small increase of the resonance amplitude and a substantial reduction in the high frequency transmissibility can be achieved by employing nonlinear stiffness in the secondary spring with respect to a linear Zener model with \(\beta _{\mathrm{l}} >1\).

Fig. 5
figure 5

The displacement transmissibility as the isolator subject to base excitations. Dashed line: linear rigid connected damper (\(\beta _{\mathrm{l}} \rightarrow +\infty \), \(\beta _{\mathrm{nl}} =0\) and \(\zeta =0.1\)); Short dashed line: linear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =5\) and \(\beta _{\mathrm{nl}} =0\)); Solid line: nonlinear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =0\), \(\beta _{\mathrm{nl}} ={25}/3\)). The markers denoted by each harmonic term were obtained from direct time integration of the nonlinear Zener model. a wide frequency range, b around resonance

Full size image
  1. (b)

    \(0\le \beta _{\mathrm{l}} \le 1\), i.e., the secondary spring is softer than the primary spring

In the second group, the displacement transmissibility curves of a linear rigidly connected damper (\(\beta _{\mathrm{l}} \rightarrow +\infty \), \(\beta _{\mathrm{nl}} =0\) and \(\zeta =0.1\)), a linear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =0.5\), \(\beta _{\mathrm{nl}} =0\)) and a nonlinear Zener model are compared. Since \(\beta _{\mathrm{l}} =0.5<1\) is studied for the linear Zener model, the nonlinear Zener model can achieve an ideal improvement. Here, the non-dimensional parameters \(\zeta =0.1\), \(\beta _{\mathrm{l}} =0\), \(\beta _{\mathrm{nl}} ={25}/{24}\) were chosen, which can have the same resonance amplitude as the linear Zener model, while the displacement transmissibility at high frequencies is reduced by 25% as shown in Fig. 6.

Fig. 6
figure 6

The displacement transmissibility as the isolator subject to base excitations. Dashed line: linear rigid connected damper (\(\beta _{\mathrm{l}} \rightarrow +\infty \), \(\beta _{\mathrm{nl}} =0\) and \(\zeta =0.1\)); Short dashed line: linear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =0.5\) and \(\beta _{\mathrm{nl}} =0\)); Solid line: nonlinear Zener model (\(\zeta =0.1\), \(\beta _{\mathrm{l}} =0\), \(\beta _{\mathrm{nl}} ={25}/{24}\)). The markers denoted by each harmonic term were obtained from direct time integration of the nonlinear Zener model. a wide frequency range, b around resonance

Full size image

4 Conclusions

In order to obtain an isolator with low resonance amplitude as well as good isolation performance at high frequencies, this paper explores the usage of nonlinear stiffness elements to improve the transmissibility efficiency of a sufficient linear damped vibration isolator, i.e., we intend to improve its original poor high-frequency isolation performance and meanwhile maintain or even reduce its already low resonance amplitude, denoted as an ideal improvement for the isolator in this paper. More specifically, a nonlinear Zener model, which is formed by replacing the linear secondary spring with a nonlinear one, is proposed and detailed analyzed by comparing its force and displacement transmissibility curves to that of other types of nonlinear isolators documented in the literature.

It is shown analytically and numerically that the nonlinear secondary spring can significantly improve the performance of the isolator: (1) For the force transmissibility as the isolator subjects to force excitations, the cubic stiffness of the secondary spring can provide an ideal improvement with respect to the linear Zener model. (2) For the displacement transmissibility as the isolator subject to base excitations, the nonlinear Zener model can substantially reduce the high-frequency transmissibility at the cost of a small increase of the resonance amplitude with respect to the linear Zener model if the stiffness of its secondary spring is larger than the primary spring (\(\beta _{\mathrm{l}} >1\)) or achieve an ideal improvement when the secondary spring is softer than the primary spring (\(0\le \beta _{\mathrm{l}} \le 1\)).

The results from direct numerical integration also confirm that it is a promising alternative approach to use nonlinear stiffness elements toward improving the vibration isolation performance of the isolators. Three main advantages to use nonlinear stiffness elements are evident:

  1. (1)

    Comparing with a nonlinear damper, a nonlinear spring mechanism is much easier to fabricate and can have a wider range of nonlinear coefficients to choose from, which will promote practical applications of vibration isolators featured with the nonlinear Zener model.

  2. (2)

    The displacement transmissibility under base excitations of the nonlinear Zener model with cubic stiffness secondary spring has a rate of 40dB/ decade at high frequencies, which outperforms those isolators with rigidly connected linear damper or rigid connected nonlinear damper (\(f_{\mathrm{d}}^{\mathrm{I}} \propto \dot{r}^{3}\)do not have isolation effects at very high frequencies, and \(f_{\mathrm{d}}^{\mathrm{II}} \propto r^{2}\dot{r}\) only provides a rate of 20dB/ decade). Meanwhile, the force transmissibility under force excitations of this nonlinear Zener model decreases at a rate of 40dB/ decade, which is the same as previous isolators with nonlinear damping (\(f_{\mathrm{d}}^{\mathrm{I}} \) and \(f_{\mathrm{d}}^{\mathrm{II}}\)).

  3. (3)

    The present isolator is developed from a sufficient damped linear Zener model, thus most unwanted nonlinear behaviors in those low damped nonlinear systems, such as jumps, high amplitudes of sub- and/or super harmonics, could be avoided or greatly suppressed.

In the present paper, we use the cubic secondary spring to improve the performance of the Zener model; however, it is obvious that this study can be easily extend to including other types of nonlinear springs. Further developments could consider other types of nonlinear stiffness in the secondary spring or focus on the design and test stage of such an isolator with discussions of parameter ranges associated with practical nonlinear mechanisms.