Nonlinear dynamics of the quasi-zero-stiffness SD oscillator based upon the local and global bifurcation analyses

Abstract

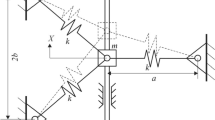
In this paper, the complicated nonlinear dynamics of the harmonically forced quasi-zero-stiffness SD (smooth and discontinuous) oscillator is investigated via direct numerical simulations. This oscillator considered that the gravity is composed of a lumped mass connected with a vertical spring of positive stiffness and a pair of horizontally compressed springs providing negative stiffness, which can achieve the quasi-zero stiffness widely used in vibration isolation. The local and global bifurcation analyses are implemented to reveal the complex dynamic phenomena of this system. The double-parameter bifurcation diagrams are constructed to demonstrate the overall topological structures for the distribution of various responses in parameter spaces. Using the Floquet theory and parameter continuation method, the local bifurcation patterns of periodic solutions are obtained. Moreover, the global bifurcation mechanisms for the crises of chaos and metamorphoses of basin boundaries are examined by analysing the attractors and attraction basins, exploring the evolutions of invariant manifolds and constructing the basin cells. Meanwhile, additional nonlinear dynamic phenomena and characteristics closely related to the bifurcations are discussed including the resonant tongues, jump phenomena, amplitude–frequency responses, chaotic seas, transient chaos, chaotic saddles, and also their generation mechanisms are presented.

Appendix

A general second-order non-autonomous dynamical system can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x} = F \left( {t,x,y} \right) , \\ \dot{y} = G \left( {t,x,y} \right) , \\ \end{array} \right. \end{aligned}$$

(8)

where F(t, x, y), G(t, x, y) are periodic in time t with the period T and are assumed to be analytic in x, y and t to guarantee the existence and uniqueness of the solution for a specific initial condition. Clearly, the discussed system in this paper is a special case of the above-mentioned dynamical system. To facilitate quick understanding of a great deal of results in this paper, some theoretical preliminaries are introduced briefly in the following:

A-1 A solution of the dynamical system (8) describes the motion starting from an arbitrary point $(x_{0}, y_{0})$ of the phase plane (x, y) when $t=t_{0}$. The solution can be written as

$$\begin{aligned} x=x(t; t_{0}, x_{0}, y_{0}), y=y(t; t_{0}, x_{0}, y_{0}), \end{aligned}$$

(9)

whose projection into the phase plane (x, y) is called a phase trajectory. To study the characteristics of phase trajectories in the phase plane (x, y) , a new definition of the rotation number $(\rho =m/n, m, n\in \mathbb {N})$ is given, that is, the bigger one between the average numbers of the points of the maximum in time history curves of (t, x) and (t, y) with respect to a period $t=nT$, which is in good agreement with the original definition of rotation number [38] but allows one to get it from the phase portrait directly. Moreover, all the frequency spectrum components of phase trajectories can be obtained by average power spectrum, which can demonstrate the change of the rotation numbers as the parameter varies. Specially, in this paper, the solution, which possesses a rotation number m / n and hence is notated by $P_{m/n}$, is referred to be harmonic resonance if $m=n=1$, subharmonic resonance of n order if $m=1, n>1$, super-harmonic resonance of m order if $m>1, n=1$, and m / n super-subharmonic resonance if $m>1, n>1$. In addition, for quasi-periodic or chaotic motion, the frequency components are no longer so simple but with $\rho$ of irrational number and continuous frequency spectrum components.

A-2 For system (8), a Poincaré section can be obtained by stroboscopically taking points $P_{n}$ at the instant $t=t_{0}+nT$, where n is an integer and $n=0$ corresponds to the starting point $p_{0}=(x_{0}, y_{0})$. Moreover, the initial phase $\theta$ of the external excitation $F{\mathrm{cos}}(\varOmega t+\theta )$ in system (2) can alter the location of the stroboscopic points in the Poincaré section, but cannot change the topological structure of an attractor that is composed of stroboscopic points. Accordingly, without loss of generality, in this paper, $\theta =0$ is taken. The solution series $\{p_{n},n\in \mathbb {Z}\}$ is classified into two cases: $\{p_{n},n=0,1,2,\ldots \}$, which is named a positive half-orbit that expresses the motion starting from $p_{0}$ as time proceeds, and $\{p_{n},n=0,-1,-2,\ldots \}$, which is called a negative half-orbit that denotes the behaviour when the time evolves inversely [38]. A set of points can be taken from the positive orbit to express the steady-state motion, that is, n tends to infinity (or say, n tends to a sufficiently large number) and meanwhile the transient state is abandoned. Hence, a discrete dynamical system on $\mathbb {R}^2$ space can be defined and used in studying the system (8), that is, the Poincaré map

$$\begin{aligned} T^n: {x_0} \longmapsto {x_n},\quad n\in \mathbb {Z}. \end{aligned}$$

(10)

It is ready to study the steady-state behaviours of system (8) through observing the points in the Poincaré section: a set of n points represents for a period-n solution, and a set of infinity points means a quasi-period or chaotic motion. The chaotic behaviours can be verified by some well-developed mathematical methods, such as Lyapunov exponent, box-counting dimension, fractal dimension, correlation dimension and averaging power spectrum. Moreover, the chaotic motion has the property that two phase trajectories starting from two very close initial conditions can diverge to each other exponentially. In addition, it has been proved that in the dissipative non-autonomous dynamical system of the second order, there is no quasi-periodic solution [38, 40] .

A-3 It is significant to obtain all the periodic solutions in a nonlinear dynamical system, which can be searched with the quasi-Newton method based upon the Poincaré map [48, 49]. The stability of a period-n orbit, which is represented by n points (each of which is termed as a period-n point) in the Poincaré section, can be determined in terms of the Floquet theory [48], which will help understand the complex bifurcation of periodic solutions. The period-n point can be treated as a fixed point with a period nT, so, without loss of generality, we only need to consider the stability of a fixed or periodic point. Assume that $p_{0}(x_{0}, y_{0})$ is a periodic point with the period T and $p(x_{0}+u, y_{0}+v)$ is a neighbouring point of $p_{0}$. For small u, v, it can be expanded into Taylor power series with the high-order terms neglected as follows

$$\begin{aligned} \left( \begin{array}{l} {\dot{u}} \\ {\dot{v}} \\ \end{array} \right) = \left( {\begin{array}{cc} {\frac{{\partial F}}{{\partial x}}} &{}\quad {\frac{{\partial F}}{{\partial y}}} \\ {\frac{{\partial G}}{{\partial x}}} &{}\quad {\frac{{\partial G}}{{\partial y}}} \\ \end{array}} \right) _{\left| {\left( {x,y} \right) = \left( {x_0 ,y_0 } \right) } \right. } \left( \begin{array}{l} u \\ v \\ \end{array} \right) . \end{aligned}$$

(11)

Integrating (11) from $t_0$ to $t_0+T$ with initial conditions $u(t_0)=1, v(t_0)=0$ and $u(t_0)=0, v(t_0)=1$, the matrix of the fundamental solution is obtained as

$$\begin{aligned} A(t) = \left| {\begin{array}{*{20}c} {u_1 (t)} &{}\quad {u_2 (t)} \\ {v_1 (t)} &{}\quad {v_2 (t)} \\ \end{array}} \right| , \end{aligned}$$

(12)

whose eigenvalues $\lambda _{i} (i=1,2)$ (Floquet multiplier, which is notated as $M_{F}$) can characterize the stability of the corresponding orbit of the periodic point in the Poincaré section. According to the Floquet’s theorem, the equation (11) has a solution with relations

$$\begin{aligned} u(t + T) = \lambda u(t), \quad v(t + T) = \lambda v(t), \end{aligned}$$

(13)

while the group of solution can be expressed with fundamental solutions as

$$\begin{aligned} u(t)=s_1{u_1(t)}+s_2{u_2(t)},\ v(t)=s_1{v_1(t)}+s_2{v_2(t)},\nonumber \\ \end{aligned}$$

(14)

which satisfy

$$\begin{aligned} \frac{{s_1 }}{{s_2 }} = \frac{{u_2 (T)}}{{\lambda - u_1 (T) }} = \frac{{ \lambda -v_2 (T) }}{{v_1 (T)}}. \end{aligned}$$

(15)

The periodic point $p_0$ is regarded as simple if both $|\lambda _{i}| (i=1,2$, and let $|\lambda _{2}|\le |\lambda _{1}|$) are unequal to 1, else it is called multiple. The simple periodic point has been classified by Levinson et al. [40] as follows: completely stable or sink if $|\lambda _{1}|<1, |\lambda _{2}|<1$, completely unstable or source if $|\lambda _{1}|>1, |\lambda _{2}|>1$, regular saddle or directly unstable if $0<\lambda _{2}<1<\lambda _{1}$ and flip saddle or inversely unstable if $\lambda _{1}<-1<\lambda _{2}<0$. This classification is complete for the system (8), because $\lambda _{1} \lambda _{2}>0$ always holds [71, 72]. For the multiple case of periodic points, if only one of $\lambda _{i}$ $(i=1,2)$ is 1, a small change of the system parameter can separate such periodic points and thus this case requires no special treatments. Additionally, the bifurcation scenarios of periodic solutions can be described with a unity circle in the complex plane: a saddle-node bifurcation or a symmetry-breaking bifurcation will occur if $\lambda _{1}$ passes the circle via 1, a period-doubling or a period-halving bifurcation (the two cases are collectively called period-doubling bifurcations in this paper) will occur if $\lambda _{1}$ goes out of the circle via $-1$, a Neimark-Sacker bifurcation will happen when $|\lambda _{i}| (i=1,2)$ come across the circle with a pair of conjunctive complex number. It is worthy to note that Levinson and Massera [39, 40] had provided the formula of numbers of periodic points for system (8), and proved that there are no quasi-periodic and completely unstable solutions in such a system with a positive damping coefficient. If we denote the total number of period-n solutions, the total number of completely stable and completely unstable period-n solutions, the number of directly unstable and the number of inversely unstable period-n solutions as N(n), C(n), D(n), I(n), respectively, then the following relations hold [38–40]:

• (a) if $n=1$,

  $$\begin{aligned} C(1)+I(1)=D(1)+1, N(1)=2D(1)+1;\nonumber \\ \end{aligned}$$

  (16)

• (b) if $n=2,4,6,\ldots$,

  $$\begin{aligned} C(n)+I(n)= & {} D(n)+2I(n/2), \nonumber \\&N(n)=2[D(n)+I(n/2)]; \end{aligned}$$

  (17)

• (c) if $n=3,5,7,\ldots$,

  $$\begin{aligned} C(n)+I(n)=D(n), N(n)=2D(n). \end{aligned}$$

  (18)

A-4 Some fundamental principles and definitions for the global bifurcations are explained briefly in the following. Firstly, the attractors contain the periodic, quasi-periodic, and chaotic ones, which can be characterized by the intersections between the phase trajectory and the Poincaré section for a periodic external forcing system. Secondly, multiple attractors often coexist with respect to different initial conditions for the same system parameters, so the collection of initial points which approach to an attractor is termed the basin of attraction of this attractor. Thirdly, there are several methods to obtain the basins of attraction, e.g. the manifold method [40, 44] and the cell-mapping method by Hsu [73, 74]. The former is utilized to explain the relations between the global bifurcations and the related dynamic phenomena in this paper. The boundary of basin of attraction is comprised of the stable manifolds of certain saddle, which is a set of initial points whose trajectories do not approach to an attractor but a saddle on the basin boundary. The pair of Floquet multipliers of the saddle can determine the directions [their slopes are $s_1/s_2$, where $\lambda _1$ and $\lambda _2$ are given in (15)] of its stable and unstable manifolds (which are also termed $\omega$-branch and $\alpha$-branch, respectively) in the Poincaré section. It is worthy to note that every point on the manifold will be mapped to a point on the same manifold if the system is integrated from the point over a period of the saddle. Hence, a start point $q_0$ on the line, which is in the direction of stable and unstable eigenvectors that are through the saddle, can be chosen to calculate the manifolds with the following procedure. Here only take the algorithm for the stable manifold as an example, and the unstable manifold can be obtained with the same routine. The start point $q_0$ is chosen on the line that is in the direction of eigenvector of the saddle and through the saddle, which also should satisfy that the return point $p_0$ of its backward time integration over a time period of the saddle is within a specified small distance $\epsilon$ to the eigenvector. Next, the new start point $q_1$ is chosen on the line between $q_0$ and $p_0$ till its integration return point $p_1$ lies within the distance $\epsilon$ of $p_0$ on the manifold. By analogy, a sequence of integration return points of proper start points, $p_2, p_3, p_4, \ldots$, can be found, which composes the stable manifold. The accuracy of calculation for the manifolds has been proved in [75]. Moreover, the return point of the point on a manifold must lie on the manifold, so an intersection of the stable and unstable invariant manifolds implies an infinite number of intersections between the two manifolds. The intersections of stable and unstable manifolds of a saddle point, or intersections of manifolds of the same group of highly periodic saddles, are called homoclinic points, while the intersections between manifolds issued from different saddles are called heteroclinic points. Homoclinic and hereroclinic points may induce a chaotic attractor [76], and similarly both homoclinic and hereroclinic points can also result in a fractal boundary of basin of attraction [64]. Additionally, it should be pointed out that two different stable manifolds never intersect each other: because if not so, it will imply an infinite number of intersections between them, and then the saddle is one of the intersection points, which apparently does not hold. Likewise, the unstable manifolds are also in the same case.

A-5 To understand the complicated metamorphosis of boundary of basin of attraction, some critical concepts and theorems are introduced in the following. As well known, the coexistence of multiple attractors is a common phenomenon in a nonlinear dynamical system. All the initial points that approach to an attractor compose the basin of attraction of this attractor. Obviously, there is basin boundary for a basin of attraction, B. To verify the complex property of basin boundary, a boundary point is firstly defined as such a point whose every open neighbourhood possesses a non-empty intersection with B and at least one other basin. All the boundary points of B constitute the boundary of B that is written as $\partial \bar{B}$. The basin boundary is fractal if it contains a transversal homoclinic point. Moreover, there exist more complex properties for some basin boundaries, such as Wada point, Wada basin and Wada property [55–59, 65]. Those boundaries involve at least three coexisting basins of attraction. Several definitions and theorems are important to prove them. First, a boundary point is a Wada point if every open neighbourhood of the point has a non-empty intersection with at least three basins. The basin is called Wada basin if each boundary point is a Wada point, while it is called partial Wada basin if only partially boundary points are Wada points. Furthermore, the Wada property of attraction basin, which usually implies strong complexity for basin boundary in the sense of predictability, denotes that each boundary point of one basin is also the boundary point of all other basins. The Wada property is based upon a theorem in [55] to supply a sufficient condition for its existence: assume p is a periodic point on the boundary such that (i) the unstable manifold of p intersects every basin and (ii) the stable manifold of p is dense in each of the basin boundaries. It is easy to understand but difficult to verify it numerically. Nusse and York [57] supplied several effective theorems to address this issue, of which two theorems used in this paper are listed in the end of this section. Only by applying the Theorem 1, it is still difficult to validate the existence of Wada basin, because we have to find all the accessible hyperbolic points, but at least it can determine the existence of partial Wada point, while, according to Theorem 2, we only need to construct basin cell for the verification of Wada basin. In the two theorems and their corollaries, an accessibility hypothesis is considered as a premise, that is, every accessible basin boundary point is on the stable manifold of certain hyperbolic periodic point. In fact, the Theorem 2 implies that the accessibility hypothesis is equivalent to the existence of basin cell [57]. To understand the theorems about basin cell, it is necessary to introduce accessible point and the construction of basin cell. We say a point p in $\partial \bar{B}$ is accessible from basin B if a curve can be plotted starting from B such that p is the first boundary point of B that the curve hits. Secondly, basin cell Q of basin B is a compact trapping region, that is, a trajectory in B once enters into Q and will never leave again. Hence, a basin cell must contain an attractor. Basin cell is constructed by pieces of stable and unstable manifolds of a periodic saddle that situates on the boundary of a basin of attraction, for which some schematic diagrams are given in [57]. Here the description about basin cell is given: assume that a group of period-n saddles $P=\{ p_{ {i}}|1\le i\le n \}$ generates a basin cell C (with boundary $\partial C$), we say, $\partial C \cap W^{\mathrm{s}}(p_i), \partial C \cap W^{\mathrm{u}}(p_i)$ are the stable and unstable edges of the cell C, respectively, and the common point of a stable and an unstable manifolds is called a corner point, while a piece of unstable manifold of $p_{ {i}}$ that links $p_{ {i}}$ and a corner point is called a supporting arc, which does not contain any other point of C. Therefore, we call a basin cell developed by a period-n saddle as a 2n-sided cell.

Theorem 1

([57]) Let p be a $B_1$-accessible hyperbolic periodic point, and assume that the unstable manifold $W^{\mathrm{u}}(p)$ intersects each $B_k$, where $1 \le k \le N$. Then (a) every point z on $W^{\mathrm{s}}(p)$ is a Wada point with respect to the basins $B_k$ ($1 \le k \le N$), (b) if the orbit of p is the only $B_1$-accessible periodic orbit, then $\partial \bar{B}_1$ is a Wada basin boundary with respect to $B_k$ ($1 \le k \le N$).

Theorem 2

([57]) Let $P_1$ be a hyperbolic periodic orbit that generates a basin cell $C_1$. Let $B_k$ ($1 \le k \le N$) be N disjoint basins ($N\ge 3$), where $B_1$ is the basin of $C_1$. Assume that the unstable manifold $W^{\mathrm{u}}(P_k)$ intersects each basin $B_k$ ($1 \le k \le N$), then $\partial \bar{B}_1$ is a Wada basin boundary with respect to $B_k$ ($1 \le k \le N$).