Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints

Abstract

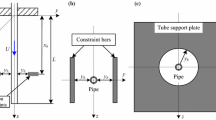
In this paper, the nonlinear dynamics of a cantilevered pipe conveying fluid interacting with two support walls on both sides is first investigated. The main goal of this study is to explore how the dynamics of a cantilevered pipe will perform in the presence of two support walls along the pipe axis. The interacting force is defined as impact in order to simulate the impacting effects for a pipe with various flow velocities. The impact force is modeled either by a cubic spring or by a trilinear spring. The nonlinear equations of motion are discretized via Galerkin’s method, and the discretized equations are solved by using a fourth-order Runge–Kutta method. Results show that the pipe would periodically impact the walls when the flow velocity is just beyond the critical value. When the flow velocity is sufficiently higher, however, the pipe may behave different patterns of contacting the walls, such as point contact and segments contact. Periodic, quasi-periodic motions, as well as chaotic oscillations are observed in such a pipe system.

Appendix

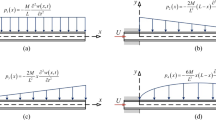
In this part, we will give the elements of the matrices mentioned in Sect. 3. As described above, the nonlinear terms in Eq. (5) may be written in Eq. (6). As can be seen that, the nonlinear terms are the multiplication of three terms, which are all related to the eigenfuncitons, such as ${\eta }^{\prime }{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }}$ and ${\eta }^{{\prime }{\prime }}\int _\xi ^1 {\int _0^\xi {{\eta }^{\prime }{\dot{{\eta }}^{{\prime }{\prime }}}\mathrm{d}\xi } \mathrm{d}\xi }$. After applying the Galerkin’s technique, the multiplication has the form of (13). After using the transforming scheme, Eq. (6) would be of that form of Eqs. (7), (8), and (9). Expressions of the elements of matrices in these equations are given below (taking ${\eta }^{\prime }{\eta }^{{\prime }{\prime }}{\eta }^{{\prime }{\prime }{\prime }}$, for example). As to the integrals of in some of the nonlinear terms, they could be applied on the corresponding terms when the transformation has been completed.

$$\begin{aligned} \mathbf{A}_L= & {} \left[ {{\begin{array}{lllll} {{\varphi }^{\prime }_1 }&{} {{\varphi }^{\prime }_2 }&{} \cdots &{} {{\varphi }^{\prime }_N } \\ \end{array} }} \right] _{1\times N} \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{B}_L= & {} \left[ {{\begin{array}{lllllllllllll} {{\varphi }^{{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }}_N }&{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }}_N }&{} &{} 0&{} &{} &{} \\ &{} &{} 0&{} &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N\times N^{2}} \end{aligned}$$

(14)

$$\begin{aligned} \mathbf{C}_L= & {} \left[ {{\begin{array}{llllllllllllllllllll} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N }&{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N }&{} &{} &{} &{} &{} &{} 0&{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N }&{} &{} &{} &{} &{} \\ &{} &{} &{} 0&{} &{} &{} &{} &{} &{} &{} &{} &{} \ddots &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} {{\varphi }^{{\prime }{\prime }{\prime }}_1 }&{} {{\varphi }^{{\prime }{\prime }{\prime }}_2 }&{} \cdots &{} {{\varphi }^{{\prime }{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N^{2}\times N^{3}} \end{aligned}$$

(15)

$$\begin{aligned} \mathbf{D}_T= & {} \left[ {{\begin{array}{llllll} {{q}^{\prime }_1 }&{} &{} &{} &{} \\ &{} {{q}^{\prime }_1 }&{} &{} 0&{} \\ &{} &{} {{q}^{\prime }_1 }&{} &{} \\ &{} 0&{} &{} \ddots &{} \\ &{} &{} &{} &{} {{q}^{\prime }_1 } \\ {{q}^{\prime }_2 }&{} &{} &{} &{} \\ &{} {{q}^{\prime }_2 }&{} &{} 0&{} \\ &{} &{} {{q}^{\prime }_2 }&{} &{} \\ &{} 0&{} &{} \ddots &{} \\ &{} &{} &{} &{} {{q}^{\prime }_2 } \\ &{} &{} \cdots &{} &{} \\ {{q}^{\prime }_N }&{} &{} &{} &{} \\ &{} {{q}^{\prime }_N }&{} &{} 0&{} \\ &{} &{} {{q}^{\prime }_N }&{} &{} \\ &{} 0&{} &{} \ddots &{} \\ &{} &{} &{} &{} {{q}^{\prime }_N } \\ \end{array} }} \right] _{N^{3}\times N^{2}}\end{aligned}$$

(16)

$$\begin{aligned} \mathbf{E}_T= & {} \left[ {{\begin{array}{lllll} {{q}^{{\prime }{\prime }}_1 }&{} &{} &{} 0 \\ &{} {{q}^{{\prime }{\prime }}_1 }&{} &{} \\ &{} &{} \ddots &{} \\ 0&{} &{} &{} {{q}^{{\prime }{\prime }}_1 } \\ {{q}^{{\prime }{\prime }}_2 }&{} &{} &{} 0 \\ &{} {{q}^{{\prime }{\prime }}_2 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {{q}^{{\prime }{\prime }}_2 } \\ 0&{} \cdots &{} \cdots &{} \\ {{q}^{{\prime }{\prime }}_N }&{} &{} &{} 0 \\ &{} {{q}^{{\prime }{\prime }}_N }&{} &{} \\ &{} &{} \ddots &{} \\ 0&{} &{} &{} {{q}^{{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N^{2}\times N}\end{aligned}$$

(17)

$$\begin{aligned} \mathbf{F}_T= & {} \left[ {{\begin{array}{l} {{q}^{{\prime }{\prime }{\prime }}_1 } \\ {{q}^{{\prime }{\prime }{\prime }}_2 } \\ \vdots \\ {{q}^{{\prime }{\prime }{\prime }}_N } \\ \end{array} }} \right] _{N\times 1} \end{aligned}$$

(18)

Substituting (13) to (18) into Eq. (9), left multiplying $\varphi _i \left( \xi \right)$ and integrating along the pipe, we would get the coefficients of the nonlinear terms.

$$\begin{aligned} \alpha _{ijkl}= & {} \int _0^1 {\left[ {u^{2}-\frac{3}{2}\gamma \left( {1-\xi } \right) } \right] \varphi _i } \varphi _j ^{\prime \prime }\varphi _k ^{\prime }\varphi _l ^{\prime }\mathrm{d}\xi \nonumber \\&-\,\frac{1}{2}\gamma \int _0^1 {\varphi _i } \varphi _j ^{\prime }\varphi _k ^{\prime }\varphi _l ^{\prime }\mathrm{d}\xi +3\int _0^1 {\varphi _i } \varphi _j ^{\prime }\varphi _k ^{\prime \prime }\varphi _l ^{\prime \prime \prime }\mathrm{d}\xi \nonumber \\&+\int _0^1 {\varphi _i } \varphi _j ^{\prime \prime }\varphi _k ^{\prime \prime }\varphi _l ^{\prime \prime }\mathrm{d}\xi \nonumber \\&-\int _0^1 {\varphi _i \varphi _j ^{\prime }\int _0^\xi {\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] \varphi _k ^{\prime }\varphi _l ^{\prime \prime \prime }\mathrm{d}\xi } } \mathrm{d}\xi \nonumber \\&+\int _0^1 {\varphi _i } \varphi _j ^{\prime }\int _0^\xi {\varphi _k ^{\prime \prime } \varphi _l^{{\prime }{\prime }{\prime }{\prime }}}\mathrm{d}\xi \mathrm{d}\xi \nonumber \\&+\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime }}\int _\xi ^1 \int _0^\xi \left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] \nonumber \\&\times \,\varphi _k ^{\prime }\varphi _l ^{{\prime } {\prime }{\prime }}\mathrm{d}\xi \mathrm{d}\xi \mathrm{d}\xi \nonumber \\&-\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime } }\int _\xi ^1 {\int _0^\xi {\varphi _k ^{{\prime }{\prime } }\varphi _l^{{\prime }{\prime }{\prime }{\prime }}\mathrm{d}\xi } } \mathrm{d}\xi \mathrm{d}\xi \nonumber \\&+\,\gamma \int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime }}\int _\xi ^1 {\varphi _k ^{\prime }\varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi \nonumber \\&-\,u^{2}\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime } }\int _\xi ^1 {\varphi _k ^{\prime }\varphi _l ^{{\prime }{\prime } }\mathrm{d}\xi } \mathrm{d}\xi \nonumber \\&-\int _0^1 {\varphi _i } \varphi _j ^{{\prime }{\prime }}\int _\xi ^1 {\varphi _k ^{{\prime }{\prime }}\varphi _l ^{{\prime }{\prime }{\prime }}\mathrm{d}\xi } \mathrm{d}\xi \end{aligned}$$

(19)

$$\begin{aligned} \beta _{ijkl}= & {} 2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{\prime }_j {\varphi }^{\prime }_k {\varphi }^{\prime }_l \mathrm{d}\xi }\nonumber \\&-\,2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{\prime }_j \int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime \prime }\mathrm{d}\xi } \mathrm{d}\xi } \nonumber \\&+\,2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{{\prime }{\prime }}_j \int _\xi ^1 {\int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime \prime }\mathrm{d}\xi } \mathrm{d}\xi } \mathrm{d}\xi }\nonumber \\&-\,2u\sqrt{\beta }\int _0^1 {\varphi _i {\varphi }^{{\prime }{\prime }}_j \int _\xi ^1 {{\varphi }^{\prime }_k \varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi }\end{aligned}$$

(20)

$$\begin{aligned} \gamma _{ijkl}= & {} \int _0^1 {\varphi _i {\varphi }^{\prime }_j \int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi }\nonumber \\&-\int _0^1 {\varphi _i {\varphi }^{{\prime }{\prime }}_j \int _\xi ^1 {\int _0^\xi {{\varphi }^{\prime }_k \varphi _l ^{\prime }\mathrm{d}\xi } \mathrm{d}\xi } \mathrm{d}\xi } \end{aligned}$$

(21)

Coefficients of the linear terms are defined as follows:

$$\begin{aligned} m_{ij}= & {} \int _0^1 {\varphi _i \varphi _j \mathrm{d}\xi } =\delta _{ij}\end{aligned}$$

(22)

$$\begin{aligned} c_{ij}= & {} \alpha \int _0^1 {\varphi _i \varphi _j ^{{\prime }{\prime } {\prime } {\prime } }\mathrm{d}\xi } +2u\sqrt{\beta }\int _0^1 {\varphi _i \varphi _j ^{\prime }\mathrm{d}\xi }\end{aligned}$$

(23)

$$\begin{aligned} k_{ij}= & {} \int _0^1 {\varphi _i \varphi _j ^{{\prime } {\prime } {\prime } {\prime } }\mathrm{d}\xi } +\int _0^1 {\left[ {u^{2}-\gamma \left( {1-\xi } \right) } \right] \varphi _i \varphi _j ^{{\prime }{\prime } }\mathrm{d}\xi }\nonumber \\&+\,\gamma \int _0^1 {\varphi _i \varphi _j ^{\prime }\mathrm{d}\xi } \end{aligned}$$

(24)

As to elements in $\mathbf{f}\left( \mathbf{q} \right)$, it is obtained by left multiplying $\varphi _i \left( \xi \right)$ and integrating along the pipe. That is:

$$\begin{aligned} f_i =\int _0^1 {\varphi _i f\left( {\sum _{s=1}^N {\varphi _s q_s } } \right) \mathrm{d}\xi }. \end{aligned}$$

(25)