Skip to main content
SpringerLink
Log in

Formulation and solution of space–time fractional Boussinesq equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

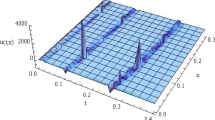
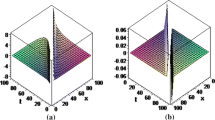
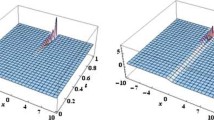
The fractional variational principles beside the semi-inverse technique are applied to derive the space–time fractional Boussinesq equation. The semi-inverse method is used to find the Lagrangian of the Boussinesq equation. The classical derivatives in the Lagrangian are replaced by the fractional derivatives. Then, the fractional variational principles are devoted to lead to the fractional Euler–Lagrange equation, which gives the fractional Boussinesq equation. The modified Riemann–Liouville fractional derivative is used to obtain the space–time fractional Boussinesq equation. The fractional sub-equation method is employed to solve the derived space-time fractional Boussinesq equation. The solutions are obtained in terms of fractional hyper-geometric functions, fractional triangle functions and a rational function. These solutions show that the fractional Boussinesq equation can describe periodic, soliton and explosive waves. This study indicates that the fractional order modulates the waves described by Boussinesq equation. We remark that more pronounced effects and deeper insight into the formation and properties of the resulting waves are added by considering the fractional order derivatives beside the nonlinearity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Baleanu, D., Tenreiro Machado, J.A., Luo, A.C.J. (eds.): Fractional Dynamics and Control. Springer, New York (2012)

    MATH  Google Scholar 

  2. Tarasov, V.E.: Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media. Springer, Heidelberg (2010)

    Google Scholar 

  3. Klafter, J., Lim, S.C., Metzler, R. (eds.): Fractional Dynamics: Recent Advances. World Scientific, Singapore (2012)

    MATH  Google Scholar 

  4. Petráš, I.: Fractional-Order Nonlinear Systems Modeling, Analysis and Simulation. Higher Education Press and Springer, Beijing and Berlin (2011)

    MATH  Google Scholar 

  5. El-Wakil, S.A., Abulwafa, E.M., El-Shewy, E.K., Mahmoud, A.A.: Time-fractional KdV equation for plasma of two different temperature electrons and ion. Phys. Plasmas 18(9), 092116 (2011)

    Article  Google Scholar 

  6. El-Wakil, S.A., Abulwafa, E.M., El-Shewy, E.K., Mahmoud, A.A.: Time-fractional study of electron acoustic solitary waves in plasma of cold electron and two isothermal ions. J. Plasma Phys. 78(6), 641–649 (2012)

    Article  Google Scholar 

  7. Tarasov, V.E.: Gravitational field of fractal distribution of particles. Celest. Mech. Dyn. Astron. 19(1), 1–15 (2006)

    Article  MathSciNet  Google Scholar 

  8. Tarasov, V.E.: Fractional generalization of gradient and Hamiltonian systems. J. Phys. A Math. Gen. 38, 5929–5943 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  9. Laskin, N., Zaslavsky, G.M.: Nonlinear fractional dynamics of lattice with long–range interaction. Phys. A Stat. Mech. Appl. 368(1), 38–54 (2006)

    Article  Google Scholar 

  10. Uchaikin, V.V.: Self-similar anomalous diffusion and levy-stable laws. Phys. Usp. 26, 821–849 (2003)

    Article  Google Scholar 

  11. Fujioka, J.: Lagrangian structure and Hamiltonian conservation in fractional optical solitons. Commun. Fract. Calc. 1(1), 1–14 (2010)

    MathSciNet  Google Scholar 

  12. Zeng, D.-Q., Qin, Y.-M.: The Laplace–Adomian–Pade technique for the seepage flows with the Riemann–Liouville derivatives. Commun. Fract. Calc. 3(1), 26–29 (2012)

    Google Scholar 

  13. Riewe, F.: Nonconservative Lagrangian and Hamiltonian mechanics. Phys. Rev. E 53(2), 1890–1899 (1996)

    Article  MathSciNet  Google Scholar 

  14. Riewe, F.: Mechanics with fractional derivatives. Phys. Rev. E 55(3), 3581–3592 (1997)

    Article  MathSciNet  Google Scholar 

  15. Agrawal, O.P.: Formulation of Euler–Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 272(1), 368–379 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  16. Agrawal, O.P.: Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A Math. theor. 40, 6287–6303 (2007)

    Article  MATH  Google Scholar 

  17. Baleanu, D., Muslih, S.I.: Lagrangian formulation of classical fields with in Riemann–Liouville fractional derivatives. Phys. Scr. 72(1), 119–123 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  18. Muslih, S.I., Baleanu, D., Rabei, E.: Hamiltonian formulation of classical fields with in Riemann–Liouville fractional derivatives. Phys. Scr. 73, 436–438 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  19. Baleanu, D., Muslih, S.I., Taş, K.: Fractional Hamiltonian analysis of higher order derivatives systems. J. Math. Phys. 47(10), 103503 (2006)

    Article  MathSciNet  Google Scholar 

  20. Baleanu, D.: About fractional quantization and fractional variational principles. Commun. Nonlinear Sci. Numer. Simul. 14(6), 2520–2523 (2009)

    Article  Google Scholar 

  21. Baleanu, D., Muslih, S.I.: On fractional variational principles. In: Sabatier, J., Agrawal, O.P., Tenreiro Machado, J.A. (eds.) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering, pp. 115–126. Springer, Dordrecht (2007)

    Chapter  Google Scholar 

  22. Klimek, M.: On Solutions of Linear Fractional Differential Equations of a Variational Type. The Publishing Office of Czestochowa University of Technology, Czestochowa (2009)

    Google Scholar 

  23. Herzallah, M.A.E., Baleanu, D.: Fractional-order Euler–Lagrange equations and formulation of Hamiltonian equations. Nonlinear Dyn. 58(1–2), 385–391 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  24. Huang, Z.L., Jin, X.L., Lim, C.W., Wang, Y.: Statistical analysis for stochastic systems including fractional derivatives. Nonlinear Dyn. 59(1–2), 339–349 (2010)

    Article  MATH  Google Scholar 

  25. El-Wakil, S.A., Abulwafa, E.M., Zahran, M.A., Mahmoud, A.A.: Time-fractional KdV equation: formulation and solution using variational methods. Nonlinear Dyn. 65(1), 55–63 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  26. El-Wakil, S.A., Abulwafa, E.M., Zahran, M.A., Mahmoud, A.A.: Formulation of some fractional evolution equations used in mathematical physics. Nonlinear Sci. Lett. A 2(1), 37–46 (2011)

    MathSciNet  Google Scholar 

  27. Tenreiro Machado, J.A., Kiryakova, V., Mainardi, F.: Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 16(3), 1140–1153 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  28. Almeida, R., Pooseh, S., Torres, D.F.M.: Fractional variational problems depending on indefinite integrals. Nonlinear Anal. 75(3), 1009–1025 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  29. Abulwafa, E.M., Elgarayhi, A.M., Mahmoud, A.A., Tawfik, A.M.: Formulation and solution of space–time fractional KdV–Burgers equation. Comput. Methods Sci. Technol. 19(4), 235–243 (2013)

    Article  Google Scholar 

  30. Almedia, R., Malinowska, A.B.: Fractional variational principle of Herglotz. Discrete Cont. Dyn. Syst. B 19(8), 2367–2381 (2014)

    Article  Google Scholar 

  31. Liu, H.-Y., He, J.-H., Li, Z.-B.: Fractional calculus for nanoscale flow and heat transfer. Int. J. Numer. Methods Heat Fluid Flow 24(6), 1227–1250 (2014)

    Article  MathSciNet  Google Scholar 

  32. Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus: Models and Numerical Methods. World Scientific, Hackensack (2012)

    Google Scholar 

  33. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier Science B.V., Amsterdam (2006)

    MATH  Google Scholar 

  34. Atanackoviç, T.M., Stankoviç, B.: Generalized wave equation in nonlocal elasticity. Acta Mech. 208(1), 1–10 (2009)

  35. Carpinteri, A., Cornetti, P., Sapora, A.: A fractional calculus approach to nonlocal elasticity. Eur. Phys. J. Spec. Top. 193(1), 193–204 (2011)

    Article  Google Scholar 

  36. Sapora, A., Cornetti, P., Carpinteri, A.: Diffusion problems on fractional nonlocal media. Cent. Eur. J. Phys. 11(10), 1255–1261 (2013)

    Article  Google Scholar 

  37. Tarasov, V.E.: Lattice model with power-law spatial dispersion for fractional elasticity. Cent. Eur. J. Phys. 11(11), 1580–1588 (2013)

    Article  MathSciNet  Google Scholar 

  38. Sapora, A., Cornetti, P., Carpinteri, A.: Wave propagation in nonlocal elastic continua modelled by a fractional calculus approach. Commun. Nonlinear Sci. Numer. Simul. 18(1), 63–74 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  39. Kolwankar, K.M., Gangal, A.D.: Local fractional Fokker–Planck equation. Phys. Rev. Lett. 80(2), 214–217 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  40. Cresson, J.: Non-differentiable variational principles. J. Math. Anal. Appl. 307(1), 48–64 (2005)

  41. Chen, W., Sun, H.G.: Multiscale statistical model of fully-developed turbulence particle accelerations. Mod. Phys. Lett. B 23(3), 449–452 (2009)

    Article  MATH  Google Scholar 

  42. Jumarie, G.: Modified Riemann–Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 51(9–10), 1367–1376 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  43. Jumarie, G.: Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Appl. Math. Lett. 22(3), 378–385 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  44. Wu, G.-C., Lee, E.W.M.: Fractional variational iteration method and its application. Phys. Lett. A 374(25), 2506–2509 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  45. Wu, G-c: A fractional variational iteration method for solving fractional nonlinear differential equations. Comput. Math. Appl. 61(8), 2186–2190 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  46. Bona, J.L., Chen, M., Saut, J.-C.: Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. I: derivation and linear theory. J. Nonlinear Sci. 12(4), 283–318 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  47. Bona, J.L., Chen, M., Saut, J.-C.: Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media: II. The nonlinear theory. Nonlinearity 17(3), 925–952 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  48. Kirby, J.T.: Boussinesq models and applications to nearshore wave propagation, surfzone processes and wave-induced currents. In: Lakhan, V.C. (ed.) Advances in Coastal Modeling, pp. 1–41. Elsevier, Amsterdam (2003)

    Chapter  Google Scholar 

  49. Jawad, A.J.M., Petković, M.D., Laketa, P., Biswas, A.: Dynamics of shallow water waves with Boussinesq equation. Sci. Iran. B 20(1), 179–184 (2013)

    Google Scholar 

  50. Mehdinejadiani, B., Jafari, H., Baleanu, D.: Derivation of a fractional Boussinesq equation for modelling unconfined groundwater. Eur. Phys. J. Spec. Top. 222(8), 1805–1812 (2013)

    Article  Google Scholar 

  51. Yıldırım, A., Sezer, S.A., Kaplan, Y.: Analytical approach to Boussinesq equation with space- and time-fractional derivatives. Int. J. Numer. Methods Fluids 66(10), 1315–1324 (2011)

    Article  MATH  Google Scholar 

  52. Abdel-Salam, E.A.-B., Yousif, E.A.: Solution of nonlinear space–time fractional differential equations using the fractional Riccati expansion method. Math. Probl. Eng. 2013, 846283 (2013)

    Article  MathSciNet  Google Scholar 

  53. El-Sayed, A.M.A., Behiry, S.H., Raslan, W.E.: A numerical algorithm for the solution of an intermediate fractional advection dispersion equation. Commun. Nonlinear Sci. Numer. Simul. 15(5), 1253–1258 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  54. Duan, J.-S., Rach, R., Baleanu, D., Wazwaz, A.-M.: A review of the Adomian decomposition method and its applications to fractional differential equations. Commun. Fract. Calc. 3(2), 73–99 (2012)

    Google Scholar 

  55. Elbeleze, A.A., Kiliçman, A., Taib, B.M.: Note on the convergence analysis of homotopy perturbation method for fractional partial differential equations. Abstr. Appl. Anal. 2014, 803902 (2014)

  56. Faraz, N., Khan, Y., Jafari, H., Yildirim, A., Madani, M.: Fractional variational iteration method via modified Riemann–Liouville derivative. J. King Saud Univ. Sci. 23(4), 413–417 (2012)

    Article  Google Scholar 

  57. Ul Hassan, Q.M., Mohyud-Din, S.T.: Exp-function method using modified Riemann–Liouville derivative for Burger’s equations of fractional-order. QSci. Connect 2013, 19 (2013)

  58. Zhang, S., Zhang, H.-Q.: Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 375(7), 1069–1073 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  59. Alzaidy, J.F.: The fractional sub-equation method and exact analytical solutions for some nonlinear fractional PDEs. Am. J. Math. Anal. 1(1), 14–19 (2013)

    Google Scholar 

  60. He, J.-H.: Semi-inverse method of establishing generalized variational principles for fluid mechanics with emphasis on turbo-machinery aerodynamics. Int. J. Turbo Jet-Engines 14(1), 23–28 (1997)

    Google Scholar 

  61. Zhang, S., Zong, Q.A., Liu, D., Gao, Q.: A generalized exp-function method for fractional Riccati differential equations. Commun. Fract. Calc. 1(1), 48–51 (2010)

    Google Scholar 

  62. Christov, C.I.: An energy-consistent dispersive shallow-water model. Wave Motion 34(2), 161–174 (2001)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Theoretical Physics Research Group, Physics Department, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt

    S. A. El-Wakil & Essam M. Abulwafa

Authors
  1. S. A. El-Wakil
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Essam M. Abulwafa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Essam M. Abulwafa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

El-Wakil, S.A., Abulwafa, E.M. Formulation and solution of space–time fractional Boussinesq equation. Nonlinear Dyn 80, 167–175 (2015). https://doi.org/10.1007/s11071-014-1858-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1858-3

Keywords

Mathematics Subject Classification

Search

Navigation