1 Introduction

Fractional-order systems have been intensively studied in various contexts [1]. In mechanical engineering, there were suggestions to apply it for various complex nonviscous, memory- effected damping effects like rubbing or composite material response including natural wooden composites. Finally, it was used to model visco-elastic properties [2–5]. Dynamic properties of beams and plates, characterized by multiple relaxation times, were also modelled by the fractional derivative in [1].

Important features of such systems include their dynamical memory of previous states, which could imply additional internal variables [6, 7]. Consequently, modelling of the system instantaneous states involves their time evolution history. Note that the memory effects combined with additional nonlinearities can be a source of hysteresis which is very common in engineering systems [1]. The fractional-order- damped rotor system with rubbing malfunction was proposed [8, 9].

On the other hand, randomly excited nonlinear systems show a number of interesting features such as stochastic Hopf bifurcation [10], period-doubling bifurcations [11] and a stochastic resonance phenomenon [12]. This resonance is characterized by the flow over the potential barrier. One of the simplest systems with such a barrier may be defined as a single degree-of-freedom, double-well Duffing potential. In such a system, the occurrence of a single-well escape is a result of competition between damping and excitation. Consequently, this escape can be associated with stochastic resonance (or coherence resonance [13]). This phenomenon is expected to be more complicated in higher system dimensions (or memory effect), which can be introduced by hidden variables of nonviscous damping [7].

Motivated by mechanical engineering applications, fractional damping effects were studied in the context of resonance conditions, synchronization effects and also appearance of chaotic solutions [14, 15]. It was found out [16] that the existence of the fractional-order derivative could affect not only damping, but also stiffness, which was characterized by equivalent damping and equivalent stiffness coefficients, respectively. The fractional calculus is going to have a fruitful field in many scientific areas. It would be adopted for the description of diffusion and wave propagation phenomenon, the system identification in robotics, telecommunications and also for control systems [17]. Recently, the phenomenon of vibrational resonance was also investigated in a wide parameter range of Duffing systems with fractional-order damping [18]. The authors [18] claimed that fractional-order damping can cause a change in a number of the stable steady states and then lead to single- or double-well resonance behaviour.

Cao et al. [19] investigated the fractionally damped system response using phase diagrams, bifurcation diagrams and Poincare maps in a wide range of the fractional order that changes from 0.1 to 2.0. Their analysis results show that the fractional-order- damped Duffing system could be treated as a bifurcation parameter. By continuing these studies, Chen et al. [20] and Hu et al. [21] analysed such a system with a bounded noise excitation term composed of harmonic excitation with an additional random phase. The authors investigated the appearance of bimodal amplitude through a corresponding probability density. This signalled the existence of a stochastic jump.

In this paper, we continue the investigations described in [20, 21]. However, in contrast to Ref. [21], we terminate the harmonic component and study the nonlinear Duffing system with a fractional derivative subjected to a random excitation force defined as generated with an additive white Gaussian noise term.

2 The model and equations of motion

Our discussion starts with the corresponding Duffing equation supplemented by additional fractional damping and random forcing

$$\begin{aligned} \frac{\mathrm{d}^2x}{\mathrm{d} t^2} + \beta \frac{\mathrm{d}^qx}{\mathrm{d} t^q} -x +x^3= f(t), \end{aligned}$$
(1)

where \(\mathrm{d}^qx/\mathrm{d} t^q\) is the Grünwald–Letnikov fractional derivative [1, 22] with an order \(q\)

$$\begin{aligned} \frac{\mathrm{d}^qx}{\mathrm{d} t^q}&= _a D^{q} x(t)\nonumber \\&= \lim _{\varDelta t \rightarrow 0} \left[ \!\! \frac{1}{(\varDelta t)^{q}} \sum _{j = 0}^{\left[ \frac{t-a}{\varDelta t} \right] } (-1)^j {q \atopwithdelims ()j\!} x(t \!-\! j\varDelta t) \!\!\right] \!. \end{aligned}$$
(2)

In Eq. 2, \(\left[ \frac{t-a}{\varDelta t} \right] \) means the integer part, where \(\varDelta t\) denotes the integration time step, and \(a\) is an arbitrary number smaller than \(t\). This defines the length of system memory. In the following analysis, we assumed \(a=0\), which corresponds to the memory length of whole trajectory. The binomial coefficients in the above sum can be expressed by the Euler’s Gamma function:

$$\begin{aligned} {q \atopwithdelims ()j}= \frac{q !}{j! (q - j)!}= \frac{ \varGamma (q+1)}{\varGamma (j+1) \varGamma ( q-j +1)}. \end{aligned}$$
(3)

Excitation force \(f(t)\) has been defined as stationary Gaussian additive white noise with standard deviation \(\sigma _f\) described by the corresponding autocorrelation function:

$$\begin{aligned} <f(t) f(t+\varDelta t')>&= 1/T_0 \int \limits _{0}^{T_0} f(t) f(t+\varDelta t') \mathrm{d} t \nonumber \\&= (\sigma _f)^2 \delta (\varDelta t'), \end{aligned}$$
(4)

where \(\delta (.)\) is the Dirac delta, \(\varDelta t'\) is an arbitrary time difference and \(T_0\) is a large time interval.

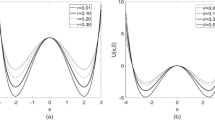
The considered potential describing the restore force in Eq. 1

$$\begin{aligned} V(x)= \frac{x^2}{2}-\frac{x^4}{4} \end{aligned}$$
(5)

is given in Fig. 1. Note that the dynamical model in Eq. 1 possesses damping and excitation terms.

Fig. 1
figure 1

Bistable potential \(V(x)\) (restore force (Eq. 1) \(F_x=-\mathrm{d} V(x)/\mathrm{d} x= x-x^3\)) used in the calculations (Eq. 5)

Full size image

The numerical algorithm used in the present calculations is created in analogy to the so-called Euler–Maruyama algorithm (see [23, 24], where the deterministic and stochastic integration parts are summed. In case of fractional-order derivative, the integration schema is given by the Newton–Leipnik algorithm [22] based on the Grünwald–Letnikov expansion (Eq. 2). Consequently, in the time discretized form \(t_n= n\varDelta t\) (for \(a=0\) used in calculations), the numerical integration is represented by the Newton–Leipnik–Maruyama algorithm:

$$\begin{aligned} \begin{aligned} x_{n}&=x_{n-1} + v_{n-1} \varDelta t, \\ z_{n}&=(\varDelta t)^{-q} \left( \sum \limits _{j=0}^{n}{c_j^{(q)} x(t_{n-j})}\right) , \\ v_{n}&= v_{n-1}+ \left( -\beta z_{n-1} +x_{n-1}-x_{n-1}^3\right) \\&\quad \quad (\varDelta t)+ \sigma _f f_n \sqrt{(\varDelta t)}, \end{aligned} \end{aligned}$$
(6)

where \(x_n\) and \(v_n\) are the time discretized displacement and velocity, \(z_n\) corresponds to the memory-dependent damping, \(f_n\) is a random number with a normal distribution and the unitary standard deviation and \(\sigma _f\) is a measure of the level of noise. Additionally, coefficients \(c_j^{(q)}\) satisfy the following recursive relations [22]:

$$\begin{aligned} c_0^{(q)}=1, \quad c_j^{(q)}=\left( 1 - \frac{1+q}{j} \right) c_{j-1}^{(q)}. \end{aligned}$$
(7)

Due to competition between dissipating and generating mechanical energy, these two terms lead to balancing the total energy at a particular level. This level could be higher or lower with respect to the energy barrier (\(\varDelta V=0.25\), see Fig. 1). This level signals also a vicinity of cross-well jump conditions in the dynamical system.

Consequently, as level \(\sigma _f\) increases, the system response (measured by a standard deviation \(\sigma _x\) of the displacement \(x\) fluctuations) would be of sufficiently larger magnitude to pass the system states through the potential barrier.

Evidently, such a jump corresponds to the bifurcation of single potential well vibration of a relatively small amplitude into cross-barrier oscillations of a fairly large amplitude.

3 Simulation results

By simulating the dynamical system (Eq. 1) with increasing noise level conditions, we followed the scenario of stochastic resonance [12, 25, 26]. For numerical calculations, the Matlab environment has been used with nondimensional parameters, where \(\beta =0.15\) is damping coefficient and excitation force represented by noise level is in range of \(\sigma _F \in (0 \div 0.3)\). The initial conditions were fixed as \(x_0=0.21, v_0=0.31\). The integration step \(\varDelta t=0.005\), simulation time interval in terms of estimated time instants \(t_n \in [0,800]\), where first \(400\) instants were cut off as a transient part.

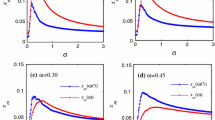
Figure 2 shows the signal-to-noise ratio versus increasing noise level \(\sigma _f\). Note that the calculations have been made for different orders of damping term \(q\). For each simulation in terms of \(q\), the averaged noise results have been plotted. The average includes its 10 different Gaussian noise realizations. It is obvious that the stochastic resonance, corresponding to the increase of maximum \(\sigma _x/\sigma _F\), is characterized by different noise level \(\sigma _f\) for different \(q\).

Fig. 2
figure 2

The displacement signals-to-noise ratio \(\sigma _x/\sigma _F\) versus noise intensity \(\sigma _F\) for different orders of derivative \(q=q_1\)

Full size image

On the way to a solution with the most frequent (coherent) jumps of the large amplitude, a single hop between potential wells occurs. This effect has been investigated in greater detail in Fig. 3, where we show the number of hops versus noise levels \(\sigma _f\) for various orders of derivative \(q\). Figure 3b illustrates the dependence of the solution transition (single hop appearance between the potential wells in simulation time) via a function of critical noise level versus an increasing order of derivative \(q\). The corresponding formula for plotting the curve presented in Fig. 3b can be expressed as a polynomial function, obtained in a standard approach by means of the least squares method:

$$\begin{aligned} \sigma _F(q)=-0.087q^2 +0.17q +0.0059. \end{aligned}$$
(8)

In Fig. 4, the mean of displacements \(<x>=1/T_0 \int x(t) \mathrm{d} t\) versus noise intensity \(\sigma _f\) for chosen orders \(q\) is plotted. Note, \(<x> \approx 0\) means that the system oscillates by hopping symmetrically through the potential barrier, while \(<x> \approx 1\) indicates that the oscillating system is trapped in one of the potential wells. Following Fig. 4a–c, one can see that as derivative order \(q\) increases, larger noise intensity is needed to reach cross-barrier oscillations. Certainly, larger \(q\) means larger damping, which stabilizes single well oscillations.

Fig. 3
figure 3

a Number of hops versus noise intensity \(\sigma _F\) for different orders of derivative \(q=q_1\); b critical curve of transitions begin between the potential wells via increasing orders of derivative \(q\) (dots)

Full size image
Fig. 4
figure 4

The mean of displacement \(<x>\) versus noise intensity \(\sigma _F\) for different orders of derivative \(q\). The other system parameters, the initial conditions and the simulation time interval are as in Fig. 3

Full size image

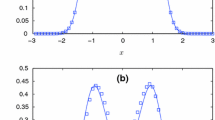
Figure 5 illustrates the selected cases of solutions shown in Fig. 2 focusing on their time evolutions. Especially, we present the phase portraits (Fig. 5a, c, e, g) and their corresponding time series (Fig. 5b, d, f, h) for increasing orders of fractional derivative \(q = 0.1\) (Fig. 5a, b), \(q = 0.3\) (Fig. 5c, d) and \(q = 0.6\) (Fig. 5e–h). The corresponding noise levels were \(\sigma _F=0.09\) and \(\sigma _F=0.3\), as in Fig. 5a–f and Fig. 5g, h, respectively.

Fig. 5
figure 5

The phase portraits (a, c, e, g) and their corresponding time series (b, d, f, h) in case of noise intensity \(\sigma _F=0.09\) for derivative orders \(q=0.1\) (a, b), \(q=0.3\) (c, d), \(q=0.6\) (e, f), and also \(q=0.6\) in case of noise intensity \(\sigma _F=0.3\) (g, h)

Full size image

Note that more localized motion in various fractional cases appear at the lower noise level (Fig. 5a–f) comparing to the frequent hopping solution comparing to the frequent hopping solution at the higher noise level (Fig. 5g, h). Long time behaviour is characterized by the increasing number of hops between potential wells with growing \(q\) (Fig. 3a). It is also worth to note a difference between Fig. 5a, b and Fig. 5e, f. For smaller \(q\) (\(q=0.1\) in Fig. 3a–b), a phase of coherent hop oscillations is visible, while for larger \(q\) (\(q=0.3\) and \(q=0.6\) in Fig. 5c, d, and Fig. 5e, f, respectively) only a single hop can be seen.

4 Conclusion

In summary, our main results indicate that the decreasing order of derivative \(q\) (Eq. 1) enhances effective damping and leads to a different response of the system analysed. Note that the present calculations were made for chosen system parameters but the final conclusion is of a general character. Namely, reaching cross-barrier oscillations in a stochastic condition and simultaneous appearance of stochastic coherence resonance can be easier for smaller \(q\) (see Fig. 2). This implies smaller damping as a result of the fractional order.