Chaos disappearance in a piecewise linear Bonhoeffer–van der Pol dynamics with a bistability of stable focus and stable relaxation oscillation under weak periodic perturbation

Abstract

This study elucidates the bifurcation structure causing chaos disappearance in a four-segment piecewise linear Bonhoeffer–van der Pol oscillator with a diode under a weak periodic perturbation. The parameter values of this oscillator are chosen such that stable focus and stable relaxation oscillation can coexist in close proximity in the phase plane if no perturbation is applied. Chaos disappearance occurs through a previously unreported novel and unconventional bifurcation mechanism. To rigorously analyze these phenomena, the diode in this oscillator is assumed to operate as a switch. In this case, the governing equation is represented as a constraint equation, and the Poincaré map is constructed as an one-dimensional map. By analyzing the Poincaré map, we clearly demonstrate why the stable relaxation oscillation that exists when no perturbation is applied disappears via chaotic oscillation when an extremely weak perturbation is applied.

Appendix

Here, we show that similar bifurcation structures demonstrated in the piecewise linear BVP oscillator under weak perturbation can be observed in a smooth BVP circuit; the governing equation of which is given by Eq. (1). This smooth model has been extensively studied.

Fig. 19

One-parameter bifurcation diagrams with $\theta _0=0.9$. a Case $\omega =1.35$ and b Case $\omega =0.3$

We set

$$\begin{aligned} k_1=0.9 \quad \mathrm{and}\quad B_0=0.21, \end{aligned}$$

(14)

and illustrate one-parameter bifurcation diagrams. To illustrate these diagrams, we define a novel Poincaré map $T_1$ as follows:

$$\begin{aligned}&T_{1}:R^2\longrightarrow R^2, \left( x\left( \frac{2\pi \theta _0}{\omega }\right) ,\; y\left( \frac{2\pi \theta _0}{\omega }\right) \right) ^{\top } \nonumber \\&\mapsto \varphi \left( \frac{2\pi \left( \theta _0+1\right) }{\omega };\ \left( x\left( \frac{2\pi \theta _0}{\omega }\right) ,\ y\left( \frac{2\pi \theta _0}{\omega }\right) \right) ^{\top }\right) \nonumber \\ \end{aligned}$$

(15)

where $\varphi (\tau ;\ (x_0,y_0)^{\top })=(x(\tau ), y({\tau }))^{\top }$ is a solution where the initial condition is $\Big (\tau _0,x_0,y_0\Big )=\Big (\frac{2\pi \theta _0}{\omega },x\Big (\frac{2\pi \theta _0}{\omega }\Big ), y\Big (\frac{2\pi \theta _0}{\omega }\Big )\Big )$. $\theta _0$ is real, which is introduced to simplify the discussion.

Fig. 20

Transient and stationary state of chaos disappearance that occur with $B_1=0.0024<B_{D1-\mathrm{smooth}}$ in the case $\omega =1.35$ and with the initial condition $(\tau _0,x_0,y_0)=(2\pi \theta _0/\omega ,1.128960834752346,0.309959180011088)$ and with $\theta _0=0.9$)

Fig. 21

a Case $\theta _0=0.9$. b Case $\theta _0=0$. c Case $\theta _0=0.1$. Special one-parameter bifurcation diagrams with $\omega =1.35$

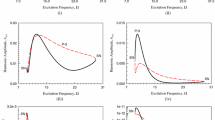
Figure 19a, b shows one-parameter bifurcation diagrams for $\omega =1.35$ and $\omega =0.3$ on the Poincaré map represented by Eq. (15), respectively, where $\theta _0=0.9$. Chaos disappearance is observed at $B_1\simeq 0.00255\cdots \equiv B_{D1-\mathrm{smooth}}$ for $\omega =1.35$, and at $B_1\simeq 0.00101\cdots \equiv B_{D2-\mathrm{smooth}}$ for $\omega =0.3$. In these figures, the initial point $(x_0,y_0)$ of the one-parameter bifurcation diagrams when $B_1=0$ is chosen such that $\dot{x}=0\ (x>0)$, i.e., $(x_0,y_0)=(1.128960834752346,0.309959180011088)$. The initial point is chosen at a location on the stable relaxation oscillation path in the absence of perturbation. Note that chaos disappearance occurs in the case $\omega =1.35$ even if $B_1=0.0024<B_{D1-\mathrm{smooth}}$ with $(\tau _0,x_0,y_0)= (2\pi \theta _0/\omega ,1.128960834752346,0.309959180011088)$ for $\theta _0=0.9$ as shown in Fig. 20, which is similar to chaos disappearance observed in the piecewise linear case, as presented in Fig. 9. In contrast, such chaos disappearance does not occur for $B_{1}<B_{D2-\mathrm{smooth}}$ with $\omega =0.3$ in the smooth case as far as the numerical results are concerned. Thus, the two distinctive routes to chaos disappearance are observed in the smooth dynamics of (1).

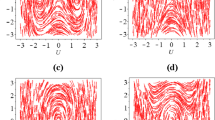
We can easily find chaos disappearance observed for $B_1<B_{D1-\mathrm{smooth}}$ in case $\omega =1.35$ presented in Fig. 20 by illustrating the special one-parameter bifurcation diagrams with changing $\theta _0$ in which the initial point is reset to a point on the stable relaxation oscillation path when no perturbation is applied, i.e., $(x_0,y_0)=(1.128960834752346,0.309959180011088)$ for every increasing bifurcation parameter $B_1$. In such special diagrams, the bifurcation structure is changed depending on the value of $\theta _0$. Changing $\theta _0$ changes the bifurcation parameter $B_1$ at which chaos disappears. The special one-parameter bifurcation diagrams are presented in Fig. 21. In contrast, the shape of these diagrams for $\omega =0.3$ do not depend on $\theta _0$, and they appear to be always the same as that in Fig. 19b.