1 Introduction

The safety level of most civil engineering structures is linked to the probability distribution of the loads they sustain while in service. In the case of dams, the main load is the volume of water stored behind the dam, which is controlled by inflow hydrograph and the spillway capacity. Spillways are designed to safely discharge the most likely values of river flows during the dam’s lifetime. The probability of having a flow larger than the spillway capacity defines the ‘accepted’ failure probability of the dam, which is kept as low as reasonably possible while considering the potential property damages and casualties. If a failure probability, p, is selected based on local legislation, then the spillway discharge which has a probability, p, of being exceeded is used as the design flow, i.e. the maximum discharge which can be safely handled by the spillway. Underestimation of the failure probability can result in unsafe structures and potentially catastrophic consequences while its overestimation can unnecessarily drive up the cost of these structures.

Several approaches have been used to calculate the design flow for a hydraulic structure:

  • Local stationary frequency analysis: annual flood peaks (or alternatively flood peaks above a fixed threshold) follow an arbitrary probability distribution for which the parameters are estimated using historical data. Parameters are assumed to be constant over time, and therefore the magnitude of the design flow for a given failure probability does not change over time (e.g. Gumbel 1958; Dunne and Leopold 1978; Singh and Strupczewski 2002).

  • Regional stationary frequency analysis: when observation series at the site of interest are inexistent or too short, the results of a stationary local frequency analysis are extrapolated to the target site using linear or non-linear regression; alternatively, observations at ‘similar’ sites can be used to estimate the parameters or a frequency distribution for which at least one parameter is regional (e.g. GREHYS 1996; Adamowski 2000; Seidou et al. 2006).

  • Non-stationary local flood frequency analysis: The assumption of stationary in both local and regional flood frequency analysis has been the norm for centuries and is still the basis for current engineering practice. However, more studies highlight that the shortfalls of stationary distributions have been published with the last few two decades (c.f. Leadbetter et al. 1983; Douglas et al. 2000). There are several reasons for flow distribution to change with time, such as change in meteorological inputs (climate change) or changes in the response of a watershed to precipitation due land-use change such as deforestation and/or urbanization. Non-stationary models have been recently proposed to account for a linear or a quadratic trend in some the parameters of extreme distributions (e.g. El Adlouni et al. 2007; Leclerc and Ouarda 2007).

  • Non-stationary regional flood frequency analysis: the principle is the same as for the regional frequency analysis, but some of the parameters are allowed to change with time (e.g. Cunderlik and Burn 2003; Cunderlik and Ouarda 2006; Leclerc and Ouarda 2007).

  • Deterministic modeling can be used when (a) a reliable model of the watershed is available and (b) meteorological inputs for that model are available or can be generated for a relatively long periods. Deterministic modeling is often used to determine the worst-case scenario without reference to a return period. The main strength of deterministic modeling is that it can readily handle any changes in input variables, such as precipitations and temperatures. Depending on the type of model used, deterministic modeling can also account for changes in land-use and human interventions on the river network. It can therefore reproduce most of the trends and cycles that are displayed in observed stream flows.

The four first approaches are clearly not suitable for providing realistic long-term distribution of flood peaks in a changing climate since stationary frequency distributions cannot be used since the statistical distributions of both precipitation and temperature are expected to change at a certain extent in the future (IPCC 2007). While the hypothesis of a linear or a quadratic trend in the parameters of a non-stationary distribution may hold for the near future, it is unrealistic for long-term projections for the simple reason that a linear trend tends toward infinite and will eventually reach unrealistic values after some time. For the case of deterministic rainfall-runoff modeling, it is well known that even with fairly accurate precipitation and temperature inputs, hydrologic models commonly miss the magnitude of the peaks (e.g. Nam et al. 2009). Usually, a hydrological model is considered ‘well calibrated’ if the Nash–Sutcliffe coefficient is above 0.7, or if the root mean square error (RMSE) of the peak flow is small compared with the mean flow. Both the Nash–Sutcliffe coefficient and the RMSE are not sensitive to a poor reproduction of extremes, if more frequent flows magnitudes are well simulated.

It is therefore hypothesized that a hydrological models that are forced with observed climate data will perform well in reproducing averaged flow over a large period D (e.g. a month), and will likely perform poorly for shorter periods. The objective of the paper is to prove that, for a given watershed and a given deterministic model calibrated on that watershed, there is a duration, D, in days and a non-stationary GEV distribution for which the parameters vary with the maximum annual D-day flow gives a better description of the exceedance probabilities stationary frequency analysis based on the simulated peaks. A demonstration of this is performed using 1970–2004 weather and flow data on the Kemptville Creek watershed, which is located in Ontario, Canada. The deterministic model used is SWAT (Soil and Water Assessment Tool), a well-known distributed physically based watershed model.

The outline of the paper is as follows: Section 2 introduces the Kemptville Creek watershed and the corresponding SWAT model. The stationary and non-stationary GEV models, the use of a non-stationary GEV model with the output of a deterministic model and the validation procedure are presented in Sect. 3. Results are presented and discussed in Sect. 4. Finally, conclusions and future directions are provided.

2 Study location and deterministic modeling

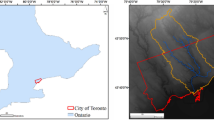
The methodology described above was applied to the Kemptville Creek watershed, which is located in Ontario, Canada. Kemptville Creek is a tributary of the Rideau River and has a drainage area of 409 km2 (c.f Fig. 1).

Fig. 1
figure 1

Location of the Kemptville Creek

Full size image

34 years or the Kemptville Creek discharges (1970–2004) were extracted from the HYDAT database and used to calibrate a SWAT model of the watershed. Daily precipitation, minimum temperature, maximum temperature data from the Environment Canada Station 6104025 (Kemptville) were used to ‘force’ the model, while soil and land-use data were downloaded from the Waterbase Project online resources (United Nations University 2010). SWAT model was calibrated using the 1970–1990 period and validated using the 1991–2004 period. Calibration and validation performance are presented in Table 1, while simulated and observed flows are plotted in Fig. 2.

Table 1 SWAT model evaluation statistics
Full size table
Fig. 2
figure 2

Observed and simulated flow

Full size image

3 Methodology

3.1 The stationary GEV distribution

The GEV distribution is used in this study to examine the flood frequency of the maximum daily flow values. The cumulative distribution function of the GEV is defined in Eq. 1.

$$ \begin{aligned} F_{\text{GEV}} (x) & = \exp \left[ { - \left( {1 - \frac{\kappa }{\alpha }\left( {x - \mu } \right)} \right)^{1/\kappa } } \right]\quad \kappa \ne 0 \\ x & = \left( {1 - \left( { - \ln (F_{\text{GEV}} (x))} \right)^{k} } \right)\frac{\alpha }{\kappa } + \mu \\ \end{aligned} $$
$$ = \exp \left[ { - \exp \left( { - \frac{{\left( {x - \mu } \right)}}{\alpha }} \right)} \right]\quad \kappa = 0 $$
(1)

Usually, the GEV distribution assumes data to be independent, identically distributed, and thus stationary (Leclerc and Ouarda 2007).

3.2 The non-stationary GEV distribution

This study will examine the case outlined in El Adlouni et al. (2007), where the location parameter, μ, and the scale parameter, α, are non-stationary.

$$ F_{\text{GEV}} (x) = \exp \left[ { - \left( {1 - \frac{\kappa }{\alpha \left( X \right)}\left( {x - \mu \left( X \right)} \right)} \right)^{1/\kappa } } \right] $$
(2)

where \( x = \left( {1 - \left( { - \ln (F_{\text{GEV}} (x))} \right)^{k} } \right)\frac{\alpha \left( X \right)}{\kappa } + \mu \left( X \right) \) and X is an external variable that modulates the parameters of the GEV distribution. In El Adlouni et al. (2007), α and μ were assumed to be linear or quadratic functions of time. In this paper, authors link α and μ to the maximum D-day average flow (denoted Q D ), as illustrated on Fig. 3.

Fig. 3
figure 3

Definition of the maximum D-day average flow

Full size image

Different models were tested in which the location parameter, μ, was assumed to be constant (i.e. μ(t) = a), to vary linearly with Q D [i.e. μ(t) = a + b × Q D (t)], or to vary linearly with time (i.e. μ(t) = a + b × t); similarly, α(t) = c, α(t) = c + d × Q D (t) and α(t) = c + d × t were included in the comparison. The shape parameter, κ, is assumed to be stationary. Table 2 lists all the models, which were included in the comparison.

Table 2 List of tested models
Full size table

3.2.1 Parameter estimation

Several methods have been proposed in El Adlouni et al. (2007) to estimate the parameters of the non-stationary GEV model; the maximum likelihood (ML), the generalized maximum-likelihood method (GML) and the Monte Carlo Markov Chain (MCMC) method. MCMC was preferred in this work because it can handle complex models and also because the ML and GML require complex theoretical developments and suffer from some limitations related to the optimization of a complex likelihood function over a changing support. MCMC is a Bayesian statistical method capable of sampling the posterior probability distributions of the parameters of a given model and which can be used instead of analytical methods when formulas are too complex to be tractable. MCMC is applied to the non-stationary GEV distribution with the Metropolis–Hasting algorithm following Stephenson (2002). The goal of the Metropolis–Hastings algorithm is to construct a Markov chain for which the equilibrium distribution is the posterior defined in Eq. 3. The generic Metropolis–Hasting algorithm can be written as follows:

  1. (i)

    Start with some initial parameter value θ0 and set i to 0.

  2. (ii)

    Given the parameter vector θ i , draw a candidate value θ i+1 from some proposal distribution.

  3. (iii)

    Compute the ratio R of the posterior density at the candidate and initial points, \( R = P(\theta_{i + 1} |{\mathbf{x}})/P(\theta_{i} |{\mathbf{x}}) \).

  4. (iv)

    With probability min(R, 1), accept the candidate parameter vector, else set θ i+1 = θ i .

  5. (v)

    Set i = i + 1 and return to step (ii).

Many versions of this algorithm have been proposed depending on the proposal distribution and the order in which the parameters are updated. In this paper, the five parameters of the non-stationary GEV distribution are updated successively with normal proposal distributions for a, b, c, d and κ. The variance parameters of the proposal distributions are tuned using a trial–error method to improve convergence speed. The Geweke (1992) test was chosen to assess the convergence of the MCMC chain because of its ease of interpretation. It is based on a test of equality of the means of the first part and the last part of a Markov chain. More details on MCMC algorithms convergence are presented in El Adlouni et al. (2006).

3.2.2 Model selection using Bayes factors

Bayes factors are powerful computational tools for comparing two competing models. They provide a weighted comparison of the likelihood of each model given observed data. The normalized Bayes factor, B kr as presented by Min and Hense (2006), compares the posterior log likelihood of the data, d, of a given model, M k, to that of the reference model, M r. This relationship is described in Eq. 2.

$$ B_{\text{kr}} = \frac{{l({\mathbf{d}}\left| {M_{\text{k}} } \right.)}}{{l({\mathbf{d}}\left| {M_{\text{r}} } \right.)}} $$
(3)

Bayes factors are an elegant way to compare competing models, but the calculation of \( l({\mathbf{d}}\left| {M_{\text{k}} } \right.) \) is rather tricky and is still the topic of intense research in applied statistics. In this paper, the authors chose to use one of the simplest methods of calculating Bayes factors from MCMC runs: the harmonic mean of the posterior distribution n as proposed by Newton and Raftery (1994), defined in Eq. 4.

$$ l(d,M_{\text{k}} ) = \frac{1}{N}\left( {\sum\limits_{m = 1}^{N} {\frac{1}{{f({\mathbf{Q}}|{\varvec{\theta}}_{m} }}} } \right) $$
(4)

where N is the length of the MCMC run, Q is the vector of observed data, \( \left\{ {{\varvec{\theta}}_{m} ,m = 1, \ldots ,N} \right\} \) is the series of parameters vectors generated by the MCMC run. The scale is presented in Table 3 used to interpret the value of a Bayes factor, B kr.

Table 3 Interpretation of Bayes factors
Full size table

In this paper, model M k is considered to be the best if B kr ≥ 1 for all possible values of r.

3.3 Comparison of the T-year floods using different models

Once the model which better fits the data has been chosen using the Bayes factors, the T-year floods of the selected non-stationary GEV model, \( Q_{T}^{\text{NSGEV}} \), are compared to the one of the stationary GEV model \( Q_{T}^{\text{GEV}} \) and the one obtained from observed data using the Weibull plotting position formula, \( Q_{T}^{\text{WEIB}} \). The comparison is performed on various time windows corresponding to the lifetime of a hypothetic structure. A time window is defined by its starting year and its length in years (20–50).

Given a time window of a length of L years starting at year y s , the T-year flood \( Q_{T}^{\text{NSGEV}} \) of the non-stationary GEV is calculated according to the algorithm presented in Fig. 4.

Fig. 4
figure 4

Algorithm used to calculate the T-year flood \( Q_{T}^{\text{NSGEV}} \) of the non-stationary GEV distribution

Full size image

The T-year flood, \( Q_{T}^{\text{GEV}} \), of the non-stationary GEV is calculated as follow:

  • Fit a GEV distribution to all the available flood peaks using ML

  • Set \( Q_{T}^{\text{GEV}} = F_{\text{GEV}}^{ - 1} \left( {1 - \frac{1}{T}} \right) \)

Given a time window of length ns stating at year y s , the empirical T-year flood can be calculated if L > T:

  • Sort the peak flows for years \( \left\{ {y_{s} ,y_{s} + 1, \ldots ,y_{s} + L - 1} \right\} \) in ascending order

  • Assign an empirical exceedance probability \( {\raise0.7ex\hbox{$i$} \!\mathord{\left/ {\vphantom {i {L + 1}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${L + 1}$}} \) equal to the observation at rank i in the sorted data

  • Using linear interpolation, find the value \( Q_{T}^{\text{WEIB}} \) corresponding to an empirical exceedance probability of \( 1 - \frac{1}{T} \).

4 Results and discussions

4.1 Stationary GEV distribution using simulated peaks

In order to assess the reliability of the simulated peaks, the T-year flood was calculated by fitting a stationary GEV distribution to the 34 years of observed peaks and the 34 years of simulated peaks. The 2-, 10-, 20-, 50-, 100- and 1,000-year flows were compared in Table 4. Results show a clear overestimation (up to 75%) of the higher return period floods and underestimation for the lower return period floods when simulated peaks are used. This highlights the risk of blindly using simulated peaks to perform for flood risk estimation.

Table 4 T-year floods using simulated and observed peaks
Full size table

4.2 Bayes factors

A total of 64 models were compared using Bayes factors, and the observations in the calibration period. The six best models are presented in Table 5, along with the stationary model and the models with time-varying parameters. The model with D = 9, location parameter varying with Q D and constant scale parameter was picked as the best among the 64 models. As the Bayes factor of the best model to model 1 (stationary model) is 204.77, it can be concluded that there is strong evidence that the selected model is better than the stationary GEV model. There is also a strong evidence that the selected model is better than model 2 (only the scale parameter varying with time: Bayes factor = 800) and model 3 (only the location parameter varying with time: Bayes factor = 14.7). There is a moderate evidence that the selected model is better than model 4 (location and scale parameter varying with time: Bayes factor = 4.52).

Table 5 Bayes factors for the six best models, and the models with time-varying parameters
Full size table

4.3 Comparison of T-years floods

The 2- and 10-year flood window calculated using the non-stationary GEV distribution, the stationary distribution using observed peaks, the stationary GEV distribution using simulated peaks and the Weibull plotting position on a 20-year sliding window is compared in Fig. 5. While the quantile calculated using the stationary GEV distribution remains constant (by construction), the ones calculated with the non-stationary GEV and the Weibull plotting position formula follow the same downward trend. The quantiles calculated with the Weibul plotting position formula come from the empirical distribution of the data and therefore are the closest estimation of the true distribution. Therefore, the non-stationary GEV provides estimates that are closer to the true risk than the stationary GEV distribution. The same results are presented on Fig. 6 for return periods of 20, 50, 100, 500 and 1,000 years, without the results from Weibull plotting position formula which cannot be computed as the return period is higher than the time window width. For all return periods, the non-stationary GEV distribution quantiles are consistently decreasing with time, just as the observed peaks. Figure 6 also illustrates the fact that using simulated peaks leads to a large overestimation of the flood risk on the Kemptville Creek for the 1970–2010 period.

Fig. 5
figure 5

2- and 10-year floods on a 20-year sliding window using the non-stationary GEV distribution, the stationary distribution and Weibull plotting position formula (W.P.P)

Full size image
Fig. 6
figure 6

Flood quantiles on a 20-year sliding window using the non-stationary GEV distribution, the stationary distribution and Weibull plotting position, for return periods 20, 50, 100 and 500 and 1,000 years

Full size image

These results clearly show that assuming that flood risk is constant leads to inadequate design of the hydraulic structures along Kemptville Creek. Therefore, new methods should be developed to better estimate flood quantiles and to be quickly considered in design codes.

4.4 Application to climate change scenarios

The methodology described in this paper can easily be extended to climate change scenarios simulations using downscaled CGM outputs. The only modification required comes from the fact that, for a given climate changes scenario (e.g. SRES A1) and a given GCM (e.g. CGCM3), statistical downscaling provides several equiprobable precipitation (minimum temperature and maximum temperature, respectively) time series. Forcing these time series in the rainfall-runoff model will result in several individual hydrographs to represent flows under a changed climate. Therefore, the max D-day average flow may be replaced by one of the following:

  1. 1.

    The mean of the max average D-day flows calculated from individual hydrographs.

  2. 2.

    The median of the max average D-day flows calculated from individual hydrographs.

  3. 3.

    Max average D-day flows calculated using the average hydrographs.

Two conditions have to be satisfied in order for the non-stationary GEV model to work: (1) there should be a period where both flow measurements and GCM predictors are available to calibrate and validate statistical downscaling equations and (2) there should be a minimum level of correlation between hydrograph downscaled climate data and observed flows to calibrate the parameters of the non-stationary GEV distribution. An application to the Kemptville Creek flows using the outputs of the third Generation Canadian General Circulation Model (CGCM3) under SERES A2 scenario is presented in the companion paper.

5 Conclusion

Several non-stationary GEV models with a time-varying location and scale parameters were compared to the Kemptville Creek watershed, which is located in Ontario, Canada. Several types of temporal variations were explored for the location and scale parameters, including linear relationships with time or SWAT-simulated maximum average flow over a D-day period. The models parameters were obtained using MCMCs, and the best model was picked using Bayes factors. Results show that (a) using the non-stationary GEV distribution with a location parameter linked to the maximum 9-day average flow provides a much better estimation of flood quantiles than applying a stationary frequency analysis to the simulated peak flows and (b) flood quantiles simulated using the non-stationary GEV distribution display the same trends as observed data on the study period.