1 Introduction

Increasingly, in the engineering profession, optimization methods and algorithms are becoming essential tools. However, employing these is in general time-consuming. This is due to the need for extensive computational power when deriving solutions through their enlistment, and rests as well in the nature of the properties of the employed methods and algorithms, themselves. The methods that are currently used (to very good effect) in deriving solutions to problems of optimization, are the gradient methods and the heuristic algorithms. Unfortunately, both procedures, in addition to their advantages, have some drawbacks either.

The advantages of employing gradient methods lies in their ability to enable the achieving of a rapid convergence to the nearest optimum—not always the global one. When used for deriving a solution to a multi-modal function through simple enlistment, very often such a local optimum is found. The disadvantages of employing these methods rests within the conditions of the objective function. This must be continuous. What is more, the Hessian function must be positive definite, while the calculations are performed with a single starting point, which, in turn, significantly restricts search area. Furthermore, the choice of the starting point has an impact on the convergence of the method, and may bring about the possibility of the results falling into a local extremes. In practice many procedures based on this paradigm, e.g. the Back-Propagation Algorithm or the Quasi-Newton methods for can be applied for various optimization tasks—in particular, for the artificial neural networks (ANN) training [26].

Metaheuristic procedures aimed at finding the global optimum (usually with a certain probability) have also been developed. To this group belong the Evolutionary Algorithms [17], the Simulated Annealing Algorithms [20], the Immunological Methods [2] and the swarm intelligence procedures [21]. The aforementioned heuristic algorithms require only knowing the formula of the cost (fitness) function, and are quite simple to implement using contemporary computing resources. Nowadays, the group of algorithms that belong within the category of swarm intelligence is very extensive. Among the latest nature-inspired metaheuristics are the Bat Algorithm [8] the Harmony Search [16], the Firefly Algorithm [7, 23], the Cuckoo Search [6, 27], the Flower Pollination Algorithm [22] and the Krill Herd Algorithm [4].

Heuristic methods are often used for neural network learning process, and they constitute an alternative methods to typical traditional gradient algorithms as, for instance, error Back-Propagation or Levenberg–Marquardt procedures. For certain types of a neural networks, these conventional methods cannot be used. This comes about due to the lack of the possibility of applying analytical derivative formulas, or because a small convergence is achieved within the learning algorithm. The Fuzzy Flip-Flop (FFF) neural network type is an example of both of aforementioned phenomena. For this type of networks, certain training algorithms have been applied, among them, the Bacterial Memetic Algorithm [19] and the Evolutionary Strategy [17]. For a typical network of a multilayer perceptron type, many heuristic optimization methods can be also employed. These range from the Genetic Algorithm, to the Evolutionary Algorithms and end with the swarm optimization procedures. An interesting example of the use of the heuristic method for learning ANN, is the procedure for the prediction of peak ground acceleration that is described in [11]. In this work, the authors applied a well-known derivatively-free global optimisation algorithm (based on a simulated annealing metaheuristic) so as to improve the neural networks efficiency. Other stimulating illustrations of employing metaheuristics for ANN learning procedure include the application of Artificial Bee Colony algorithm [14, 15], Differential Evolution [3] or plain Particle Swarm Optimization procedure [12, 13]. From the results found within scientific publications, it can be concluded that very often after using the heuristic algorithm, we obtain positive results much faster than when applying gradient methods [16].

The use of the Krill Herd Algorithm (KHA) have become very popular recently [5]. This is because it represents an effective modern optimisation and search procedure [4, 9]. This metaheuristic technique is based on the behaviour of a krill herd [10]. The purpose of this paper is to investigate the possibility of applying the KHA for parameters’ optimization purposes within ANN. In our work, the results of numerical studies performed on the typical benchmark dataset, were compared with other heuristic methods, and with a gradient algorithm.

The outline of this paper is as follows. Following this introduction, in Sect. 2, information about the Krill Herd Algorithm (KHA) is to be introduced, while in Sect. 3, that of the neural network and the tuning of its structure and parameters by means of the KHA will be presented. Subsequently, In Sect. 4, application examples will be presented. Finally, conclusion will be drawn in last part of this work.

2 Krill Herd Algorithm

In this chapter, the optimization algorithm covered by this paper will be briefly described. KHA is one of the newest optimization procedures that come with a heuristic character. Its main inspiration lays in following and imitating the biological swarming behaviour of the Antarctic Krill (Euphausia superba), found in the Southern Ocean. This algorithm was introduced in 2012 by Gandomi and Alavi [4].

The Krill metaheuristic is used in solving optimization tasks. This consists of finding the extreme point for the function f, called the ’fitness function’ or the ’cost function’. In essence KHA procedure is based on observing such behaviors in the herd as foraging and communicating with other members of the swarm. Therefore, the position of the particular individuals \((i=1,\ldots ,M)\) in the herd is described through the following equation:

$$\begin{aligned} \frac{\textit{dX}_i}{dt}=N_i+F_i+D_i, \end{aligned}$$
(1)

The Lagrangian model (1) contains three components: \(N_i\) denotes the motion induced by other individuals within the swarm, \(F_i\) is the foraging motion and \(D_i\) provides the physical diffusion of i-th krill. The movement effected by the presence of other krill can be described using the following formula:

$$\begin{aligned} N_i=N^{\textit{max}} \alpha _i+ \omega N_i^{\textit{old}}. \end{aligned}$$
(2)

In Eq. (2) individuals try to maintain a high density within the herd and move in a direction induced by the \(\alpha _i\) parameter. It is calculated taking into account local effects such as swarm density, and also a global character that is based on the best krill position. Here \(N^{max}\) denotes the maximum induced speed. Additionally, parameter \(\omega \), the induced motion inertia weight, is present. This quantity reveals the importance of the \(N_i^{old}\) values from the previous iteration, when determining the new value \(N_i\). Information on the values of the particular parameters listed here can be found in [4].

The foraging motion includes two main components:

$$\begin{aligned} F_i=V_f \beta _i +\omega _f F_i^{old}, \end{aligned}$$
(3)

where the first one represents a mechanism in which individual krill informs the other swarm members about a new food source location, while the other describes the swarm’s previous experience with respect to prior food location. Furthermore, quantity \(V_f\) describes the speed of searching for food, and has been established empirically in previous studies on KHA—to generally recommended value of 0.02 [4]. The location of a food source is the quantity that for KHA, is dependent upon the basis of the distribution of the fitness function and the individual krill position. It is given by the following equation:

$$\begin{aligned} X^{food}=\frac{\sum _{i=1}^{M}\frac{1}{f_i}X_i}{\sum _{i=1}^{M}\frac{1}{f_i}}. \end{aligned}$$
(4)

The physical diffusion part for each individual is an introduced random factor which is formulated as follows:

$$\begin{aligned} D_i=D^{max} \left( 1-\frac{I}{I_{max}} \right) \delta \end{aligned}$$
(5)

Here, I is the index of current iteration, \(I_{max}\) indicates a maximum number of iterations, \(D^{max}\in [0.002; 0.1]\) represents the maximal diffusion speed, while \(\delta \) constitutes the random directional vector, with its elements belonging to the interval \([-1; 1]\).

Finally, for each krill, its location at time \(t+\Delta t\) is determined as follows:

$$\begin{aligned} X_i(t+\Delta t)= X_i(t)+\Delta t \frac{dX_i}{dt } \end{aligned}$$
(6)

where \(\Delta t\) is the scaling factor alternating the speed of solution space exploration.

At the last stage of the KHA procedure, genetic operators are used [25]. Doing so, primarily classical mutation and crossover operators known from Genetic Algorithms are employed. In other studies [24], alternative operators based on Differential Evolution are also proposed.

In this research the crossover results in a change of the mth coordinate of ith krill as shown below by the formula:

$$\begin{aligned} x_{i,m} =\left\{ \begin{array}{c c c} x_{r,m} &{} \text {for}&{}\gamma \le Cr \\ x_{i,m} &{} \text {for}&{} \gamma > Cr\\ \end{array} \right. \end{aligned}$$
(7)

where \(Cr=0.2 \hat{K}_{i,best}\); \(r \in \{1,2,\ldots ,i-1,i+1,\ldots ,N \}\) denotes a random index, and \(\gamma \) is a random number from the interval [0, 1) generated according to the uniform distribution. In this approach the crossover operator is alternating a single individual.

The mutation modifies the mth coordinate of the ith krill in accordance with the formula:

$$\begin{aligned} x_{i,m} =\left\{ \begin{array}{c c c} x_{gbest,m}+ \mu (x_{p,m}-x_{q,m}) &{} \text {for} &{} \gamma \le Mu \\ x_{i,m} &{} \text {for} &{} \gamma > Mu \end{array} \right. \end{aligned}$$
(8)

where \(Mu=0.05 / \hat{K}_{i,best}\); \(p,q \in \{1,2,\ldots ,i-1,i+1,\ldots ,K \}\) and \(\mu \in [0,1)\).

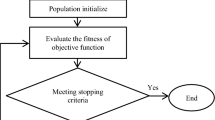
This phase is optional, implementation of these operators can be completely omitted or only one of them can be employed. As shown by certain preliminary tests [4], the KHA achieves the best results with an implemented differential crossover operator. Generally, the KHA procedure can be described by an introduced flowchart as in Fig. 1. Additional information about the KHA can be found in [18, 25].

Fig. 1
figure 1

Flowchart of the Krill Herd Algorithm

Full size image

3 KHAs Application for Tuning Neural Network’s Parameters

An optimization procedure based on the KHA described in section 2 has been applied for the training of an Artificial Neural Network (ANN), and the obtained results were compared with the ones obtained by using: Back Propagation (BP), the Genetic Algorithm (GA) and the Harmony Search (HS) taken from article [16]. In the KHA-based training method, all weights and biases from ANN translate into a vector. This represents the position of an individual krill. In our study, the initial conditions for a krill position are obtained using a random value generator with uniform distribution. Moreover, in the presented research, the parameters of KHA were adopted based on literature [4] and [18]. In particular, the following parameters were assumed: \(N^{max}=0.01, V_f=0.02, \omega =2.0, \omega _f=2.0\) and finally \(D^{max}=0.7\). In addition, for each example, the scaling factor associated with element dt was determined individually. Here the training process is terminated when maximal epoch number has been reached. In this study, it was set as 100.

For the purposes of ascertaining the fitness of the studied algorithms, as the value of the fitness function a Sum of Square Error over training (SSE) was considered. However for the classification task a more representative practice is using the Classification Error (CE), hence, naturally it was selected as a second quality measure:

$$\begin{aligned} {\textit{CE}}=\frac{\textit{err}_T}{P}100 \end{aligned}$$
(9)

where \(\textit{err}_T\) denotes the total number of misclassifications and P is the number of examples under classification. It should be clearly emphasized that the choice of both measures is not accidental. This because generating the minimum value of SSE error does not always entail a marked decrease in the CE error. This can be explained by considering the construction of a neural network. Here, the output layer is a set of neurons representing each of the considered classes. The result of classification is, hence, designated by way of an index of neurons of the highest output value, thus reducing—during the learning phase—the value of the output signals, which in turn decrees the overall SSE error, while not always having an impact on the CE error. To circumvent this, weighted (with factors 0.5) error containing both types of errors (SSE and CE) is being employed here.

4 Numerical Experiments

For the numerical verification of the proposed algorithm, classification for selected benchmark data sets was carried out. These data sets come from the well-known UCI Machine Learning Repository [1]. Detailed information related to the cardinality of the learning and testing samples, the number of classes, as well as the dimensionality and the structure of the ANN, can be found in Table 1.

Table 1 Data sets used for verification
Full size table

Additionally, it should be emphasized here that the last two sets are characterized by having a very large imbalance in the multiplicity of examples within the considered classes.

For the classification of the individual data sets, ANN were constructed. Their structure is based on the comparative study conducted in article [16]. Thus, all tested networks have three layers, and all neurons have an applied tanh transfer function. Moreover, input-output data values were normalized to be in the range \([-1, 1]\).

In order to generate a comparison with the other results, the data sets were divided up as follows: \(80~\%\) of all samples constituted learning data, while the rest represented the testing data. Naturally, these proportions were maintained for each class. For every data set, the main learning algorithm was executed 20 times, using the KHA procedure with the same parameters as described in the previous section. The exception here is a factor for a scaling step associated with \(\delta t\). This was individually set for each of the considered data sets, and was used as 2.0, 3.0, 3.7, 3.0 respectively.

All parameters used in this investigation were based on recommendations that were already provided in the literature [4, 18]. What is more, the selection variable factor was based on the pilot runs tests. In the case of the first two sets of benchmarks (ie. Iris and Ionosphere), the cardinality of the population was 50, while in other cases, this figure was set to 70 individuals.

In Table 2 all numerical results were included. Furthermore, the outcomes obtained were divided into two parts. The first of these is related to the neural network learning process, and therefore it contains information about the lowest SSE errors and the lowest CE errors, in addition to the number of iterations (epochs) in which these errors were archived. The second part of the table, consists of results for the testing phase obtained for the best networks—in case of all training algorithms. No standard deviations for referenced methods were included in cited references. However, in case of KHA they were enclosed in Table 2. It can be seen that method offer relatively stable performance on run-to-run basis.

Table 2 Results at learning and testing process
Full size table

5 Discussion of Results

For the well-known Iris Set, a neural network which perfectly classifies the elements of the test set was obtained. At the same time, the smallest CE error for training set was also observed in case of KHA. It amounts to \(0.41~\%\) which corresponds to one element of the 120 examples contained within this part of the data. Comparable performance can be achieved with the BP method however in this case 1254 training algorithm iterations are needed (while KHA achieves better result requiring only 30 iterations). Full convergence curve of the optimization process for KHA was illustrated by Fig. 2. It depicts mean error values obtained for the first 40 iterations of the learning algorithm calculated over 20 tests.

Fig. 2
figure 2

Mean error values obtained within 40 iterations of neural network learning process for classification of Iris Data Set

Full size image

The original Ionosphere Data contains 34 elements in the feature vector, but one coordinate in all cases was found to be equal to 9, therefore, it was removed from the data set. Accordingly, a neural network with a simple structure \(33{-}4{-}2\) was examined. In this particular case, the first class is represented by \(64~\%\) of the examples, so it can be seen that this data set is significantly unbalanced. In the learning process, the lowest SSE error type (within heuristic method groups) was achieved for KHA. This, amounted to 31.0. On the other hand, CE and testing errors were not so impressive. But, the time of learning that comes about through using the other methods (which take much time to bring about the desired result) possibly indicates that the structure of this data is very complex. In Fig. 3, convergence of the process of determining the weights of neural network was illustrated. The optimization process fairly quickly (in 80 iteration) reaches the final level, and further training, brings only a negligible increase in the quality of classification. At this point it is worth noting that such a fast train network can be a good starting point for a different heuristic strategy in particular related to the finding a local minimum.

The Glass Data set represent six types of glass. In this case, it must be emphasized that the first and second class contain \(70~\%\) of all the data’s examples. In Fig. 4 the convergence of neural networks learning process was presented. From the graph it can be seen, that within 20 iteration the learning process is saturated and further training practically does not change the quality of the neural classifier. In dealing with this set, the proposed algorithm obtained the smallest SSE error of learning, and, in addition, the training process lasted only 21 epochs. Moreover, the set’s CE error is smaller than in the case of employing GA, but greater than that of the other methods.

The last of the considered data sets was called Thyroid. In this case, a very hard classification problem has to be solved as the first class consists of \(92.57~\%\) examples. What is more, the neural network has been designed with a \(21{-}15{-}3\) structure. This results in that the optimized problem is represented by 378 parameters. As a performance measure mean optimization error calculated over 20 tests in Fig. 5 was shown. The shape of the curve on this chart is constant in some intervals. We suppose that the main reason for this, is the high dimensionality of the examined problems and the indicated distinguishing between learning and testing within the Thyroid Data Set. Here, the data set is distinguished between the learning set and testing. Consequently, in each test, the data set should not be divided in random ways. In these tests, we obtain the best results for the learning process, and with respect to the results of KHA testing, we achieved the best result of heuristic methods that were examined. This result should be particularly emphasized, given such a high dimensionality examined task. Most methods of heuristic algorithms can not deal with such complex tasks.

Fig. 3
figure 3

Mean error values obtained within 100 iterations of neural network learning process for classification of Ionosphere Data Set

Full size image
Fig. 4
figure 4

Mean error values obtained within 40 iterations of neural network learning process for classification of Glass Data Set

Full size image
Fig. 5
figure 5

Mean error values obtained within 60 iterations of neural network learning process for classification of Thyroid Data Set

Full size image

In summary, and in consideration of the results achieved in our work, it should be stressed out that the specific data that was used for the classification task was predominantly complex, multidimensional and multimodal. Despite this, neural classifiers were optimized by KH-based method in much less time than for other heuristic algorithms or the gradient method of BP. Indeed, in Table 2, for example we can see that in the case of the Iris dataset, the execution time is a half of that of the time of a learning process based on the GA method. Simultaneously the BP classic method took a vast amount of time: about 42 times more iterations then that of the proposed algorithm. Similar observations can be drawn for the other data collections.

In conclusion, proposed algorithm gives the best result among both heuristic and classical gradient procedures for Iris dataset. In the case of the other data collections, the obtained result is the best among all the heuristic methods examined. It must be said, however, that an exception here is the Ionosphere dataset. In this case the approach based on neural network classifier generates significant classification error. We cautiously deduce that is due to the large number of features found within the vector representing examined phenomenon.

6 Conclusions

Our study reveals that, although at first glance, seemingly quite complex KHA can be employed to obtain very quickly, satisfactory results for ANN training. Hence, we believe that the proposed method represents a promising tool for neural classification. With regards to its utilization, in some cases classical gradient method (BP) was shown to yield better results, but the iteration number of its execution was incomparably bigger.

Furthermore, this method can be used when working with many types of neural networks, especially those for which the gradient learning method cannot be applied or in situations wherein its use evokes poor results in terms of training procedure convergence. In particular KHA can be very useful in case of neural networks with unique transfer (activation) function or the ones with diverse set of functions used in neural network’s layers. FFF neural network constitutes an example of network possessing such properties.

The positive results generated through the application of the KHA procedure for supervised learning in the neural network domain, has been brought about by the fact that the applied metaheuristics is based on three main components. These are: the singular movement of individuals within the swarm as affected by the presence of other swarm members; the swarm’s individual and collective foraging movements; and the individual swarm member’s random diffusion within the swarm. These actions describe the mutual influence on the individual swarm member’s position, as well as the environmental impacts of the individual and the entire swarm. The first two actions contain both global and local optimisation functions. These components, working together, constitute an optimisation strategy, which improves the results of the KHA procedure. Additionally, a randomised search operation (given as random diffusion), and two evolutionary operators (mutation and crossover) are added to the main algorithm so as to create a powerful and effective optimization procedure. Because of the aforementioned elements, the algorithm is built upon an appropriate balancing between exploration and exploitation of solution space.

What is more, during the numerical study, we discovered that the KHA procedure showed a fairly sizeable sensitivity to some internal parameters. This issue was initially considered in [18]. We feel that this issue alone constitutes another advantage of the proposed approach.

Further studies will be focused upon discerning alternative fitness measures taking into account sample imbalance. Planned future experiments will also involve using datasets of a mixed-type nature. Furthermore, in a subsequent part of planned investigation, the KHA procedure designed for optimizing structure and parameters of an ANN of FFF type, will be developed. In this case, the proposed method will be employed for the prediction of both time series data and data streams. The main intent of these tests will be to demonstrate the advantages of applying the proposed method, with respect to utilizing other classic algorithms.