1 Introduction

Gearbox is a core component of variable-speed drive applied in machinery and its operation condition is crucial to other relevant parts or even the whole mechanical system. Any abnormal state of gearbox can cause serious damage or disaster. Therefore, the investigation on the running condition monitoring of gearbox is significant and has attracted the attentions of many scholars and technicians. To date, some methods and theories have been reported for the condition monitoring of gearbox, such as the side-band algorithm (Zappala et al. 2014) and latent nestling method (Urrego et al. 2013). In addition, the work in literature (Mohanty and Kar 2006) completed the multistage gearbox fault diagnosis in combination with the discrete wavelet transform and demodulation of motor current waveform. In Bafroui and Ohadi (2014), the wavelet entropy and Shannon entropy were used as the input characteristics of artificial neural networks (ANNs) in the fault detection of gearbox under the conditions of varying speeds.

Sensors have been used to obtain the state information of the monitored object. In the application of sensors for gearbox monitoring, the traditional way is to measure the vibration signal using an acceleration sensor (Hang et al. 2014). Alternatively, some scholars attempted to use other types of sensor to obtain useful information. For example, Hamilton et al. (2014) employed the active pixel sensors to monitor the lubrication system of gearbox. Acoustic emission sensor was adopted in Li et al. (2012) to extract the fault signals in split-torque gearbox. By employing the traction drive as the sensor and measuring the relation between the torque and position, recent work (Wolf et al. 2013) completed the evaluation of gearboxes for an electrified vehicle.

The extensive studies on sensor applications provide a valuable fundamental for the acquisition of accurate condition information. However, unnecessary increase of the quantity and type of sensors can lead to information redundancy (Hang et al. 2014; Altaf et al. 2014; Seraji and Serrano 2009) or even dimension disaster (Han et al. 2005). Hence, in the condition monitoring of mechanical equipment for some complex systems, it is necessary to select optimal sensors with appropriate numbers, types, and installation positions from the given sensor network to provide the most valuable information at the lowest cost. Here, it is called the sensor network optimization problem. Besides, the optimal design of sensor network is also an important guarantee of the performance improvement of condition monitoring and fault diagnosis systems (Cheng et al. 2010; Yang et al. 2013). For example, the frequency response and experimental modal analysis were used as the theoretical basis for the sensor network optimization of a power transmission system in previous work (Nimityongskul and Kammer 2009; Worden and Burrows 2001). With the finite element technology, a bearing vibration simulation model was established and applied to sensor optimal placement for the bearing fault diagnosis (Cao et al. 2012). In addition, the Bayesian networks and the frequency response theory were proposed for sensor optimal selection (Jin et al. 2012).

However, the above methods are applicable to the selection of sensors from the network which is composed of the same type sensors only. Their applications in the multi-type sensor network are limited. In practice, sensor network optimization often subjects to some constraints, such as the cost of sensors and requirements of performance indices of the testing system. So, the sensor network optimization belongs to the constrained optimization problem. According to the directed graph model, the problem of sensor network design was studied in Raghuraj et al. (1999), Venkatasubramanian et al. (2003) under the rule of fault observability and resolution, where a mixed-integer linear programming formulation was reported. Previous work (Bhushan and Rengaswamy 2000; Li and Upadhyaya 2011; Li et al. 2012) investigated the sensor distribution problem using fault diagnostic observability and reliability criteria based on directed graph symbols. Later, a new mathematical model was proposed under the constraints on fault detection rate and isolation rate (Azam et al. 2004). Korkali and Abur (2013) proposed the development of a practical and an effective strategy for rendering the transmission grid ‘ fault-observable ’ by the optimal sensor deployment technique. The aforementioned literatures proposed some thoughts to solve the optimization problem of heterogeneous sensors. However, the failure of sensors themselves and their influences on the model for fault diagnosis have not been considered.

Essentially, the sensor network optimization belongs to a 0–1 combinatorial integer optimization problem and it is also a NP-hard problem (Li et al. 2012). Some researchers have focused on various solving algorithms, such as the principal component analysis (Li and Upadhyaya 2011; Li et al. 2012), ANNs (Chow et al. 2011; Martin et al. 2005), and Bayesian networks (Jin et al. 2012; Pourali and Mosleh 2013). Recently, some swarm intelligent optimization algorithms, e.g., particle swarm optimization (Pan and Wei 2010; Kulkarni and Venayagamoorthy 2010), genetic algorithm (GA) (Liu et al. 2008; Casillas et al. 2013), ant colony optimization (Fu 2009), artificial bee colony algorithm (Mini et al. 2014), and artificial fish-swarm algorithm (Tao et al. 2013) have been applied to solve the problem and some promising results have been successfully achieved. As a novel swarm intelligent algorithm, the shuffled frog leaping algorithm (SFLA) is a genetic-based, heuristically cooperative search algorithm (Eusuff and Lansey 2003), and it has been widely employed in various optimization fields, such as the water distribution network design (Eusuff and Lansey 2003), parameter identification (Ahandani 2014), unit commitment problem (Barati and Farsangi 2014), distribution network reconfiguration problem (Jazebi et al. 2014), and so on. In accordance with the differences in the complexity of targeted applications and problems, some improved methods have been developed. For instance, a differential operator was introduced into the evolutionary process of SFLA to solve parameter identification problems in Ahandani (2014). A binary SFLA was proposed to solve the unit combination problem in Barati and Farsangi (2014). A new SFLA was presented for continuous-space optimization in Zhen et al. (2009), where the population is divided based on the principle of uniform performance of memeplexes (communities) and all the frogs participate in the evolvement by keeping the inertia learning behaviors and learning from better ones selected randomly. In addition, the work (Chen et al. 2013) proposed a hybrid algorithm which integrates the low-discrepancy sequences, improved SFLA, and sequential quadratic programming to solve the non-convex, multi-dimensional constraint of dynamic economic dispatch problem. More recently, a new multi-objective improved shuffled frog leaping algorithm has been proposed and successfully applied to investigate the distribution feeder reconfiguration problem from the reliability enhancement point of view (Kavousi-Fard and Akbari-Zadeh 2013).

It is well-known that, constructed by basic operators such as selection, crossover, and mutation, GA (Holland 1992) can adaptively search for the optimal solution of a problem by simulating the evolution process. Inspired by GA, a new improved discrete SFLA (ID-SFLA) with crossover operator and mutation operator is proposed in this paper. The ID-SFLA is then applied to derive an intelligent solution for sensor network optimization based on the fault-sensor dependence matrix and some constraints of condition monitoring system. The effectiveness of the reported algorithm is verified by extensive experimental studies.

The remaining parts of the paper are organized as follows. The mathematical model of sensor network optimization is developed in Sect. 2. Section 3 introduces the principle of SFLA and D-SFLA, and presents the steps and flow charts of ID-SFLA inserted GA’s operators. The superiority of ID-SFLA over conventional D-SFLA and GA is demonstrated by a comparative study. As an intelligent algorithm, it is then applied to obtain the optimal sensor set for the condition monitoring of gearbox based on fault diagnosis in Sect. 4. Experimental comparative investigations with GA and D-SFLA have been conducted. Sect. 5 concludes this paper.

2 Sensor network optimization model based on dependence matrix

2.1 Fault-sensor dependence matrix

Fault diagnosis or condition monitoring of any facility relies greatly on the information collected by the sensors. Improper sensor configuration and selection may lead to serious consequences because some faults cannot be detected or not sensitive to some sensors. So, the condition monitoring system, which is composed of various sensors, must ensure that it can effectively identify all the faults. Then, the correlation needs to be established between the failures mode set and sensors set, which is called fault-sensor dependence matrix (Bagajewicz et al. 2004). Assume that a system has n failure modes (or fault sources) which can be denoted as the set F = {F 1 ,F 2 ,…,F n }. The optional sensors number is m and can be denoted as the set S = {S 1 ,S 2 ,…,S m }. The fault-sensor dependence matrix of the system can be written as binary matrix D = [d ij ], as shown below:

figure a

where i = 1,2,…,m, j = 1,2,…,n. In this matrix, each column represents the faults which can be detected by a sensor and each row represents sensors which can detect a fault. When the fault F j can be detected or measured by the sensor S i , d ij  = 1 is defined, otherwise, d ij  = 0. The dependence matrix D clearly describes the connections of each fault (F j ) and a sensor (S i ). Thus, it indicates that the fault will affect the reading of the corresponding sensor. At the same time, D is the foremost basis of sensor network optimization for complex system.

2.2 Optimization objective and constraints

In the process of state monitoring and fault diagnosis to mechanical power and transmission system like gearbox, sensor network optimization (selection) is always frequently restricted by the price, location, and installation way of sensors. Especially, for the conditions with limited fund and close price of each sensor, the priority objective is to find a cost-optimal sensor set for mechanical equipment that provides a good estimate of the state of the system and detects and locates a pre-established set of faults.

Let X = {x i } = [x 1 , x 2 ,…, x m ]T be the column vector of binary elements as a candidate solution that denotes whether the ith sensor is selected (x i  = 1) or not selected (x i  = 0). Suppose that each sensor cost is c i . With this definition, the cost function becomes

$$ \begin{array}{*{20}c} { \hbox{min} } & {C(X) = \sum\limits_{i = 1}^{m} {c_{i} x_{i} } } \\ \end{array} . $$
(1)

The observability, detection rate, resolution, and isolation rate of failure mode are the important indexes of monitoring system (IEEE 2004), and they are used as the constraints of the sensor network optimization. The definitions are shown as follow:

  1. 1.

    Fault observability (FO) (Bagajewicz et al. 2004)

Fault observability refers to the ability that a fault can be effectively observed by one or more sensors of candidate set when it occurs. To ensure that all failure modes can be observed, the result of the dot product any column (F k ) of the fault-sensor dependence matrix and optional sensors set X must be at least equal to 1. If it is equal to zero, then it shows that the failure mode is not observed by the candidate set X. That is, the following equation is satisfied

$$ FO(k) = F_{k} \cdot X = \sum\limits_{i = 1}^{m} {x_{i} d_{ik} } \ge 1,\quad \forall k \in F. $$
(2)
  1. 2.

    Fault detection rate (FDR)

The fault in sensor itself will affect the reliability of the monitoring system. The symbol p(s i ) is used to represent the prior probability of sensor S i ’s failure and p(f j ) represents the prior probability of fault F j . If fault F j occurs, the prior probability detected by sensor S i would be denoted by the symbol p(fs ij ). Assume that each sensor is independent and they detect each fault in the form of parallel connection. According to the reliability theory of parallel model (Pandey and Sarkar 2002), the probability p(d j ) of correctly detecting each fault mode can be calculated as follows

$$ p\left( {d_{j} } \right) = 1 - \prod\limits_{i = 1}^{m} {\left[ {1 - p\left( {fs_{ij} } \right)\left( {1 - p\left( {s_{i} } \right)} \right)x_{i} d_{ij} } \right]} . $$
(3)

Within the prescribed time, the ratio of the total number of correctly detected fault to the number of incorrectly detected fault by the measuring system is defined as FDR. According to IEEE Standard 1522 (2004), FDR of actual measuring system must be not less than the given index D req . The mathematical form can be expressed as follows:

$$ FDR = \frac{{\sum\nolimits_{j = 1}^{n} {p\left( {f_{j} } \right)p\left( {d_{j} } \right)} }}{{\sum\nolimits_{j = 1}^{n} {p\left( {f_{j} } \right)} }} \ge D_{req} $$
(4)
  1. 3.

    Fault resolution (FR)

The different fault modes may have the same type of symptoms. Thus, in the design of the actual condition monitoring system, the selected sensors set must not only observe failure mode, but also distinguish the different mode. Thus, the term ‘resolution’ has been used to refer to the ability of determining exactly which process fault occurred, given the set of symptoms (Bagajewicz et al. 2004).

Consequently, more faults can be distinguished only if one of them has at least one sensor that is different or does not sense the other faults at all. Specifically, concerning two different fault modes F k and F l , their corresponding columns are b k and b l in the matrix D. This is achieved by imposing the following conditions

$$ FR = \hbox{max} (b_{k} \cdot X,b_{l} \cdot X) - (b_{k} \otimes X) \cdot (b_{l} \otimes X) \ge 1,\quad 1 \le k,l \le n,k \ne l $$
(5)

where the symbol ⊗ denotes Hadamark product of two vectors.

  1. 4.

    Fault isolation rate (FIR)

According to IEEE (2004), the definition of FIR is the rate of the correctly isolation fault number to all detected fault number within the prescribed time. In the actual measuring system, FIR must be not less than the given index I req . Considering the effects of sensor fault of itself, the constraint is described as follows:

$$ FIR = \frac{{\sum\limits_{j = 1}^{n} {\left[ {p\left( {f_{j} } \right)\prod\limits_{i = 1}^{m} {\left( {1 - p\left( {s_{i} } \right)x_{i} d_{ij} } \right)} } \right]} }}{{\sum\limits_{j = 1}^{n} {\left[ {p\left( {f_{j} } \right)\left( {1 - \prod\limits_{i = 1}^{m} {p\left( {s_{i} } \right)^{{x_{i} d_{ij} }} } } \right)} \right]} }} \ge I_{req} $$
(6)

To sum up, the mathematical description of the sensor placement optimization model is the synthesis of the objective and constraints as stated above. In fact, the satisfaction of required measuring indexes on FDR and FIR can bring the lowest cost of selected sensors combination from candidate set. Simultaneously, the system can ensure that all fault modes are observed and the given fault is correctly distinguished.

3 SFLA and its improvement

This section systematically introduces the framework of SFLA and its improvements. The comparison of calculation results based on different algorithms is presented.

3.1 SFLA

As a relatively new intelligent algorithm, the SFLA was firstly proposed by Eusuff and Lansey (2003). It is based on the memetic meta-heuristic to solve the water distribution network design by the analogy similarity of the frog foraging behavior and optimization problems. A brief review of the algorithm is shown below. More details can be referred to Eusuff and Lansey (2003).

An initial population of P virtual frogs is generated randomly in the R-dimensional feasible space (R variables) and each frog is the possible solution. A frog i is represented as U i  = (U i1,U i2,…,U iR ). Then, all frogs are sorted in a descending order in terms of their fitness values f(U i ) and the entire population is divided into m p memeplexes, each containing n p frogs and meeting P = m p  × n p . The evolutionary process of SFLA contains elements of local exploration and global information exchange as follows:

Local exploration First, the best fitness value in the entire population is recorded as the global optimal frog U g . Then, q frogs in each memeplex are selected with a selection strategy and a submemeplex is formed. For each submemeplex, the frogs with the worst and best performance of fitness are identified as U w and U b , respectively. The U w is updated as below:

$$ s = \left\{ {\begin{array}{*{20}l} {\hbox{min} [r(U_{b} - U_{w} ),s_{\hbox{max} } ]} \hfill & {U_{b} - U_{w} \ge 0} \hfill \\ {\hbox{max} [r(U_{b} - U_{w} ), - s_{\hbox{max} } ]} \hfill & {U_{b} - U_{w} < 0} \hfill \\ \end{array} } \right. $$
(7)

where s is the updated step size, r is a random number in the range [0, 1], and the parameter s max is the maximum step size allowed to be adopted by a frog after being infected. s max actually serves as a constraint to control the SFLA’s global exploration ability, and an appropriate value of s max is critical to the performance of SFLA (Eusuff and Lansey 2003). The new frog is then generated by

$$ U_{\text{w}}^{\prime } = U_{\text{w}} + s $$
(8)

The fitness value of the new frog \( U_{\text{w}}^{\prime } \) is computed. If f(\( U_{\text{w}}^{\prime } \)) is better than the old f(U w ), then U w is replaced by \( U_{\text{w}}^{\prime } \). Otherwise, the calculations in Eqs. (7) and (8) are repeated with respect to the global best frog, i.e., U b is replaced by U g . If no improvement becomes possible in this case, then a new frog is randomly generated to replace it. This operation is repeated until the required number of local iterations N l in all memeplexes is satisfied.

Global information exchange Once the local exploration is completed for all memeplexes, the frog populations are re-arranged in accordance with the new fitness values for a global information exchange. Then, the entire frogs are re-partitioned into m p memeplexes and a new local exploration starts again. The operation terminates when the global iteration numbers N g or the convergence criterion is satisfied.

After all the steps of SFLA are fulfilled, the global best frog is the optimal solution of the problem.

3.2 D-SFLA

In the above algorithm, the population update method is suitable to solve the problem with continuous variables, which is also known as continuous SFLA (C-SFLA). But the sensor network optimization is 0–1 discrete integer problem and the operations should be adjusted as follows:

Step 1 :

The initial virtual population is created as the form binary random frogs of R dimension, denoted as U B

Step 2 :

When the algorithm is in the process of local exploration, the binary frogs \( U_{g}^{B} \), \( U_{b}^{B} \), and \( U_{w}^{B} \) are first converted to the decimal frogs U g , U b , and U w , respectively. Then, the update operation in accordance with Eqs. (7) and (8) is carried out. At last, the updated decimal worst frog \( U_{\text{w}}^{\prime } \) is re-converted into the binary form \( U_{w}^{B\prime } \). Other operations are the same as the C-SFLA

The algorithm with these operations aims to solve the discrete variables problem and it is called discrete SFLA (D-SFLA).

3.3 ID-SFLA

In the update strategy of C-SFLA or D-SFLA, only the local optimum frog U b (\( U_{b}^{B} \)) or the global optimal frog U g (\( U_{g}^{B} \)) is used to update the worst frog U w (\( U_{w}^{B} \)), and the effective information of other frogs in the population is not fully used. So, it is easy to reduce the differences of the population, slow the rate of convergence of the algorithm, and fall into the local optimum and cause premature phenomenon.

In this paper, according to the characteristics of 0–1 problem, the crossover and mutation operators of GA (Holland 1992) are inserted into in the local exploration. So, the update strategy is defined as follows:

Step 1 :

To improve the convergence speed of algorithm, the \( U_{b}^{B} \) and \( U_{g}^{B} \) in each submemeplex are selected as two objectives of the crossover operator (Holland 1992). One or more points are randomly chosen as crossover positions, and then, the segments of each other are simply swapped. The fitness values of two new frog produced by this method are calculated respectively. The better performance of frogs is selected as \( U_{w}^{B\prime } \), which is ready for updating \( U_{w}^{B} \);

Step 2 :

If the fitness value f(\( U_{w}^{B\prime } \)) is superior to f(\( U_{w}^{B} \)), then \( U_{w}^{B\prime } \) replaces \( U_{w}^{B} \) and the local exploration in this submemeplex will stop. Otherwise, the local mean of q binary frogs in this submemeplex, denoted as the \( U_{la}^{B} \), is computed as shown in Fig. 1. The numbers of occurrence of 0 and 1 on each bit of binary frogs are counted. If the number of 0 is larger than the number of 1, i.e., b3, the value of corresponding bit of \( U_{la}^{B} \) is 0. Otherwise, i.e. b1, the value is 1. But, if the occurrence probability of 0 and 1 is the same, i.e. b4, the bit can be randomly generated as 0 or 1. The specific calculation result of \( U_{la}^{B} \) is shown in Fig. 1.

Fig. 1
figure 1

The result of U B la with q = 4 and R = 8

Full size image
Step 3 :

Calculate the Hamming distance between \( U_{la}^{B} \) and \( U_{w}^{B} \), the mutation operator is applied to \( U_{w}^{B} \). The farther their Hamming distance is, the greater the mutation probability of \( U_{w}^{B} \) is. After the mutation, a new frog \( U_{w}^{B\prime } \) is generated and it is ready for updating \( U_{w}^{B} \) again;

Step 4 :

If step 3 can produce a better result, then replaces \( U_{w}^{B} \) with the new \( U_{w}^{B\prime } \). Otherwise, the local exploration is stopped by randomly generating a new binary frog to replace \( U_{w}^{B} \).

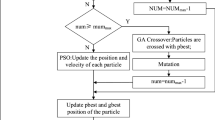
It is seen from the above steps that the parameter s max is an adaptive step size and it is no longer used in the ID-SFLA of inserted GA operators. In the basic C-SFLA or D-SFLA, the different values of s max can often lead to the different calculation results. So, in a way, the ID-SFLA can effectively reduce the influence of inappropriate parameter setting on the algorithm performance. But the other parameters are the same to the SFLA or D-SFLA. The flow charts of ID-SFLA are shown in Figs. 2 and 3.

Fig. 2
figure 2

The global exploration flow chart of ID-SFLA

Full size image
Fig. 3
figure 3

The flow chart of local exploration of ID-SFLA

Full size image

3.4 Verification with simulation studies

In order to verify the algorithm’s convergence and accuracy in problem solving, two examples are used for testing. In this paper, all the algorithms are programmed with the MATLAB (R2009a version) software and they are run with Windows XP operating system on a personal computer.

Example 1

Minimize the function

F(x) = −9x 1 + 3x 3 + 3x 5 + 12x 1 x 3 + 12x 1 x 4 + 48x 2 x 4 + 36x 2 x 6 + 60x 4 x 6 subject to

$$ \begin{array}{*{20}l} {x_{1} + x_{2} = 1} \hfill \\ {x_{3} + x_{4} = 1} \hfill \\ {x_{5} + x_{6} = 1} \hfill \\ {x_{i} \in \left\{ {0,1} \right\},\quad i = 1,2, \ldots ,6} \hfill \\ \end{array} $$
(9)

It is a relative simple 0–1 integer problem with 6 variables (R = 6) (Zhou et al. 1997). The parameter settings of D-SFLA are designated as follows: m p  = 5, n p  = 5, q = 4, N l  = 20, N g  = 20, and s max  = 3. In order to facilitate comparison, the parameter values of ID-SFLA are exactly the same to the setting of D-SFLA. The dependent parameters of GA are listed as follows. The population scale: M ga  = P = 25, crossover probability: p c  = 0.7, mutation probability: p m  = 0.03, and the maximum evolutional generation: T = 20. The length of chromosome is exactly equal to that of the frog dimension R. The three algorithms are run independently by 30 times and the corresponding results are shown in Table 1, where x* denotes the optimal solution, and F min is the minimum function value according to the x*. The fast, slow, and mean denote the fastest, the slowest, and the mean of iteration numbers, respectively. The mean convergence curves are shown in Fig. 4a.

Table 1 Comparison of calculation results of Example 1
Full size table
Fig. 4
figure 4

the mean convergence curves based on GA, D-SFLA, and ID-SFLA

Full size image

In this model, the fitness function of four intelligent algorithms is directly converted by the objective function. Zhou et al. (1997) adopts the tabu search algorithm (TSA) and only finds out one solution. On the contrary, the GA, D-SFLA, and ID-SFLA can all accurately seek out three solutions of x* and have a satisfactory global search ability. For such a relative simple question, there is not much difference in the convergence rates of D-SFLA and ID-SFLA, and they are higher than the GA. But the accuracy of the solutions from the three algorithms is exactly the same.

Example 2

The 0–1 knapsack problem is a classical integer linear programming problem and belongs to NP-hard (Martello et al. 2000). Its model is described as follows:

$$ {\text{Maximize }}Z = \sum\limits_{i = 1}^{d} {p_{i} } x_{i} $$

subject to

$$ \begin{array}{*{20}l} {\sum\limits_{i = 1}^{d} {w_{i} x_{i} \le V} } \hfill \\ {x_{i} \in \{ 0,1\} ,\quad i = 1,2, \cdots ,d} \hfill \\ \end{array} $$
(10)

where a subset of d given items has to be packed in a knapsack of capacity V. Each item has a profit p i and a weight w i . The problem is to select a subset of the items whose total weight does not exceed V and whose total profit is a maximum. Without loss of generality, assume that all input data are positive integers. Introduce the binary decision variables x i , where x i  = 1 if item i is selected and otherwise, x i  = 0.

Let d = 20, V = 878, W = {w i } = {92, 4, 43, 83, 84, 68, 92, 82, 6, 44, 32, 18, 56, 83, 25, 96, 70, 48, 14, 58}, and P = {p i } = {44, 46, 90, 72, 91, 40, 75, 35, 8, 54, 78, 40, 77, 15, 61, 17, 75, 29, 75, 63}.

It is a relatively complicated 0–1 integer problem with 20 variables (R = 20). The fitness functions of the three algorithms are converted by constructing the penalty function approach, which the constraints as penalty items are integrated into the original objective function (Radac et al. 2014). The parameters of the three algorithms are set as follows: m p  = 25, n p  = 25, q = 17, N l  = 50, N g  = 300, M ga  = 625, T = 300. The other parameter values are the same to the settings in Example 1. The calculation results are shown in Table 2. The mean convergence curves of the three intelligent algorithms are shown in Fig. 4b when N g  = 1–100.

Table 2 Comparison of calculation results of Example 2
Full size table

The standard solution of the above problem is Zmax = 1024. Table 2 and Fig. 4b show that for the complex problems, the speed and accuracy of convergence with D-SFLA have been affected heavily due to the limitation of its own local exploration mechanism. Its performances are the worst among the three algorithms and D-SFLA becomes unavailable already. But the performances of ID-SFLA are superior to D-SFLA and GA in all aspects. The comparison results show that the ID-SFLA as proposed in this paper is effective and superior.

4 Application on sensor network optimization of gearbox

According to the related theory and algorithms discussed above, the experimental model has been carried out on the sensor network optimization of condition monitoring system for a two-stage gearbox.

The faults set is F = {F 1 ,F 2 ,F 3 ,F 4 ,F 5 ,F 6 ,F 7 ,F 8 ,F 9 ,F 10 }, where F 1 —Fracture of gear tooth; F 2 —Wear-out of gear tooth; F 3 —Plastic deformation of gear tooth; F 4 —Surface fatigue of gear tooth; F 5 —Gear burns; F 6 —Imbalance of Gear shaft; F 7 —Misalignment of gear shaft; F 8 —Bearing failure; F 9 —Serious oil leakage of lubrication system; F 10 —Oil degradation of lubrication system. The prior probability set of 10 fault modes is {p(f j )} = {0.10, 0.18, 0.12, 0.12, 0.08, 0.05, 0.05, 0.20, 0.05, 0.05}. The candidate sensors set of the monitoring system is S = {S 1 ,S 2 ,S 3 ,S 4 ,S 5 ,S 6 ,S 7 ,S 8 ,S 9 ,S 10 ,S 11 ,S 12 ,S 13 ,S 14 ,S 15 ,S 16 ,S 17 ,S 18 }, where S 1 –S 6 are six different sensors which are used to monitor the various vibration signals of gearbox; S 1 —Acoustic emission sensor; S 2 —Ultrasonic sensor; S 3 —Eddy current displacement sensor; S 4 —Hall transducer sensor; S 5 —Micro-machined resonant acceleration sensor; S 6 —Magnetic grating transducer (sensor). Three sensors, S 7 –S 9 , are used to measure the gear shaft torque on the different positions of gearbox, and they indicate the slipring sensor, the rotating transformer sensor, and the infrared torque sensor, respectively. S 10 –S 12 are the three different sensors which are used to test the gearbox oil composition, and they are the viscosity sensor, the moisture sensor, and the particle sensor, respectively. S 13 –S 15 are respectively represented the wireless temperature sensors, the integrated temperature, and the digital sensor. S 16 –S 18 are different optical sensors, and they are designated based on the fiber, the grating, and the laser, respectively.

The schematic diagram about the initial locations of 18 sensors on the gearbox is shown in Fig. 5. The prior probability set of the 18 sensors’ failure is {p(s i )} = {0.02,0.03,0.05,0.01,0.02,0.01,0.04,0.03,0.01,0.02,0.01,0.03,0.02,0.03,0.025,0.02,0.01,0.015}. Referring to Zhong and Huang (2007), the matrix P_FS, which indicates the prior probability set {p(fs ij )}, is designated as follows:

Fig. 5
figure 5

The initial locations of 18 sensors on the gearbox

Full size image
$$ P\_FS = \left[ {\begin{array}{*{20}c} {0.98} & {0.99} & {0.99} & {0.98} & {0.98} & {.0.99} & {0.98} & {0.98} & {0.00} & {0.00} \\ {0.99} & {0.98} & {0.97} & {0.98} & {0.98} & {0.97} & {0.96} & {0.98} & {0.13} & {0.08} \\ {0.98} & {0.99} & {0.98} & {0.99} & {0.98} & {0.98} & {0.98} & {0.97} & {0.20} & 0 \\ {0.90} & {0.90} & {0.90} & {0.93} & {0.95} & {0.96} & {0.98} & {0.98} & {0.04} & 0 \\ {0.85} & {0.90} & {0.90} & {0.90} & {0.90} & {0.90} & {0.91} & {0.97} & 0 & {0.02} \\ {0.90} & {0.85} & {0.90} & {0.94} & {0.99} & {0.94} & {0.91} & {0.95} & {0.04} & {0.01} \\ {0.98} & {0.85} & {0.98} & {0.90} & {0.90} & {0.75} & {0.75} & {0.75} & 0 & 0 \\ {0.98} & {0.80} & {0.98} & {0.90} & {0.90} & {0.75} & {0.75} & {0.75} & 0 & {0.05} \\ {0.98} & {0.85} & {0.98} & {0.90} & {0.90} & {0.75} & {0.75} & {0.75} & {0.01} & 0 \\ 0 & {0.80} & {0.90} & {0.99} & {0.90} & 0 & 0 & {0.05} & 0 & {0.99} \\ 0 & {0.85} & {0.90} & {0.98} & {0.91} & 0 & {0.05} & 0 & 0 & {0.98} \\ 0 & {0.80} & {0.90} & {0.97} & {0.91} & 0 & 0 & {0.06} & 0 & {0.98} \\ {0.75} & {0.75} & 0 & {0.75} & {0.90} & 0 & {0.03} & 0 & {0.98} & {0.75} \\ {0.75} & {0.75} & {0.02} & {0.75} & {0.90} & 0 & 0 & 0 & {0.97} & {0.75} \\ {0.75} & {0.75} & 0 & {0.75} & {0.90} & 0 & 0 & {0.05} & {0.99} & {0.75} \\ {0.70} & {0.08} & {0.12} & 0 & {0.91} & 0 & 0 & 0 & 0 & {0.75} \\ {0.70} & {0.03} & 0 & 0 & {0.90} & 0 & {0.06} & 0 & {0.14} & {0.75} \\ {0.70} & {0.05} & 0 & {0.03} & {0.90} & 0 & 0 & 0 & 0 & {0.75} \\ \end{array} } \right] $$

In general, the cost of a sensor c i depends on two factors. One is the price itself and the other is the installation cost according to the complexity on the different positions of monitoring system. Based on this, the set of 18 sensors cost is {c i } = {1.0, 0.8, 0.6, 0.8, 0.7, 0.9, 0.5, 0.55, 0.9, 0.7, 1.0, 0.55, 0.65, 1.1, 0.4, 0.3, 0.5, 0.3} in this paper.

The specific index of the condition monitoring system for the gearbox has the following requirements: FDR is not less than 98 %; FIR is more than or equal to 95 %; all fault modes must be observed; when two or more fault modes are detected, F 4 must be correctly distinguished from F 2 and F 3 , F 6 is distinguished from F 7 , and F 8 is distinguished from F 9 and F 10 .

First of all, according to the field experiments and the correlation of actual fault and sensors on the different location positions, the fault-sensor dependence matrix D is established as shown below.

$$ D = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 1 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] $$

Then, two main problems should be solved in the sensor network optimization of gearbox with the intelligent algorithms, such as ID-SFLA and D-SFLA.

1. The preliminary setting of population scale Each frog corresponds to a possible sensors combination (solution) and its dimension R depends on the size of sensors set. In this paper, the number of the candidate sensors is 18. Thus, R = 18. In general, the frog population scale depends on the complexity of the concerned problem. The more complicated the problem is, the lager the scale is. According to the recommended value in the literature (Eusuff et al. 2006) and the actual computing cost, the part of the preliminary parameters of D-SFLA and ID-SFLA are set as m p  = 30, n p  = 30, q = 20, N l  = 50, N g  = 200, and consequently the scale is P = 900.

To facilitate the performance comparison of the three algorithms, the population scale M ga is equal to P and the evolution number T is equal to N g in GA. The other parameters are also the same to Example 2.

2. The construction of fitness function Due to the inequality constrains in the mode of sensor network optimization, a new fitness function needs be designed to guide the evolution process of the intelligent algorithms. The constraints, i.e. formulas (2) and (4)–(6) are integrated into the original objective function, i.e. formula (1), as the penalty items to complete unconstrained transformation and form a fitness function, i.e., a new objective function, as follows:

$$ \begin{aligned} \hbox{min} F\left( {X,Q} \right) & = C\left( X \right) + Q_{1k} \times \hbox{max} (0,1 - FO(k)) + Q_{2} \times \hbox{max} (0,D_{req} - FDR) + Q_{3} \times \hbox{max} (0,1 - FR) \\ & \quad + Q_{4} \times \hbox{max} (0,I_{req} - FIR) \\ \end{aligned} $$
(11)

where, k = 1,2,…,10, Q is the penalty factor and Q 1k  = Q 2  = Q 3  = Q 4  = 500 in this research.

The calculation results of the three algorithms are shown in Fig. 6 and Table 3. It can be seen that the ID-SFLA is obviously superior to the other two algorithms in terms of solving accuracy as well as solving speed and it has the excellent stability. But the solution based on GA is not available due to its low accuracy and large error. Although the accuracy of the solution based on D-SFLA has been improved, the success rate is still not high and the stability of the algorithm is poorer. According to statistics, in the 20 times of independent calculation process, the number of times of finding the minimum (F min  = 1.6) is only 10 and the success rate is 50 %. As further seen from Fig. 6b, the fastest speed is N g  = 2 and the slowest speed is N g  = 107 when it finds the optimal solution based on ID-SFLA method. It also reveals the effectiveness of ID-SFLA and the excellent ability to jump out of local optimum.

Fig. 6
figure 6

The convergence curves. a The average convergence curves of different algorithms; b the different convergence curves based on ID-SFLA

Full size image
Table 3 Calculation results of three algorithms
Full size table

According to the results of ID-SFLA, the minimum cost of the condition monitoring system on the gearbox is 1.6 and the optimal solution is x* = [0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0]T, which means that the selected sensors set is the {S 5 , S 7 , S 15 }. The FDR and FIR of actual monitoring system meet the requirements, as shown in Table 4. By calculation, FO and FR can also be satisfied. The number of actual chosen sensors is far less than the number of the candidate. The results of sensor placement optimization greatly reduce the test cost and the complexity of the measurable design. Meanwhile, it also demonstrates the effectiveness and superiority of the ID-SFLA, which is an intelligent algorithm for the sensor placement optimization model.

Table 4 Indicators of actual monitoring system on gearbox
Full size table

3. Result and effect of parameter selection It is known that the different problems probably require different parameter selections (or combinations). Like most heuristics approaches, the optimal parameter values usually cannot be obtained through theoretical calculations, but the relatively satisfactory (or better) values can be obtained from substantial experimental results. In this section, the effect of parameter selection on the results of the sensor network optimization problem is tested. Referring to the literature (Eusuff et al. 2006), the variation ranges of four parameters on ID-SFLA are listed as shown Table 5. As mentioned above, the global optimum value of the problem is F min  = 1.6. If ID-SFLA can search for F min  = 1.6 within N g  = 300, it is a successful search process. The mean computation time of ID-SFLA significantly increases with the values of parameter m p , n p and N l . But the success rate is more sensitive to the numbers of memeplexes, m p. The smaller the value of m p is, the lower the success rate becomes. When the m p is greater than or equal to 30, it has been maintained at 100. Considering the success rate and computation time, the ID-SFLA parameters as used in the above problem are reasonable.

Table 5 Results of ID-SFLA parameter selection testing for sensor network optimization of gearbox
Full size table

5 Conclusions

In this paper, a new improved discrete shuffled frog leaping algorithm (ID-SFLA) has been developed by introducing the crossover operator and mutation operator of GA into the update strategy of conventional SFLA. The results of two typical test functions show that the proposed ID-SFLA has excellent global optimization ability, faster convergence speed, and higher convergence precision than the existing one. Thanks to the adaptive step size of ID-SFLA, it is unnecessary to set up the parameter of the maximum step size s max like in C-SFLA or D-SFLA. Therefore, it can effectively avoid affecting the calculation result due to the improper setting of the parameter s max . Moreover, the model of sensor network optimization for the purpose of system state monitoring is established on the basis of fault-sensor dependence matrix of gearbox, which is used as the research objective. By comparing the optimal searching results of GA, D-SFLA, and ID-SFLA, it is found that the reported ID-SFLA can effectively solve the problem as compared with both GA and D-SFLA. The presented algorithm can be easily extended to other related domains as well.