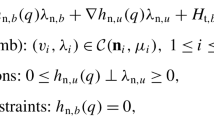The contact problem in Lagrangian systems subject to bilateral and unilateral constraints, with or without sliding Coulomb’s friction: a tutorial

Abstract

This work deals with the existence and uniqueness of the acceleration and contact forces for Lagrangian systems subject to bilateral and/or unilateral constraints with or without sliding Coulomb’s friction. Sliding friction is known to yield singularities in the system, such as Painlevé’s paradox. Our work aims at providing sufficient conditions on the parameters of the system so that singularities are avoided (i.e., the contact problem is at least solvable). To this end, the frictional problem is treated as a perturbation of the frictionless case. We provide explicit criteria, in the form of calculable upper bounds on the friction coefficients, under which the frictional contact problem is guaranteed to remain well-posed. Complementarity problems, variational inequalities, quadratic programs and inclusions in normal cones are central tools.

Appendices

Appendix A: Some convex analysis and complementarity theory tools

Let $f: \mathbb {R}^{n} \rightarrow \mathbb {R}\cup\{+\infty\}$ be a convex proper and lower semi-continuous function. Its subdifferential, denoted as $\partial f(\cdot)$, is the set of its subgradients. For a set $K$, its indicator function is $\varPsi_{K}(x)=0$ if $x \in K$ and $=+\infty$ if $x \notin K$. If $K \subset \mathbb {R}^{n}$ is a nonempty closed convex set, then its normal cone at $x$ is $N_{K}(x)=\{ z \in \mathbb {R}^{n} \mid z^{T}(y-x) \leq0\;\mbox{for all}\;y \in K\}=\partial\varPsi_{K}(x)$. If $K=\mathbb {R}^{n}$, then $N_{K}(x)=\{0\}$ for all $x$. The tangent cone $T_{K}(x)=\{z \in \mathbb {R}^{n} \mid z^{T}y \leq0\;\mbox{for all}\;y \in N _{K}(x)\}$. If $K=\{x \in \mathbb {R}^{n} \mid f(x) \geq0\}$ for $m$ continuously differentiable functions $f_{i}: \mathbb {R}^{n} \mapsto \mathbb {R}$ that satisfy the Mangasarian–Fromovitz constraint qualification [19], then $T_{K}(x)=\{v \in \mathbb {R}^{n} \mid v^{T} \nabla f_{i}(x) \geq0\ \mbox{for all}\;i\in\{1,\dots,m\}\; \mbox{such that}\;f_{i}(x)=0\}$. A linear complementarity problem $\mathrm{LCP}(q,M)$ with unknown $x \in \mathbb {R}^{n}$ is: $x \geq0$, $Mx+q \geq0$, $x^{T}(Mx+q)=0$. More compactly, $0 \leq x \perp Mx+q \geq0$. An LCP is said to be solvable if it has at least one solution. A matrix $M$ is a P-matrix if and only if the LCP has a unique solution for any $q$ [16]. A mixed linear complementarity problem (MLCP) is a problem of the form: find vectors $x,y$ such that $M_{11}x+M_{12}y+q _{1}=0$ and $0\leq x \perp M_{21}x+M_{22}y+q_{2} \geq0$ for given matrices $M_{ij}$ and vectors $q_{i}$. Let $C$ be a (unnecessarily convex) set of $\mathbb {R}^{n}$; then its dual set is $C^{*}=\{x \in \mathbb {R}^{n} \mid x^{T}z \geq0\;\mbox{for all}\;z \in C\}$, which is always a closed convex cone. Let $M \in \mathbb {R}^{n\times n}$ be a symmetric positive definite matrix defining the inner product $x^{\mathrm{T}} \, M \, x$. With this metric, the orthogonal projection of a vector $x \in \mathbb {R}^{n}$ on a convex set $K \subset \mathbb {R}^{n}$ is denoted as $\mathrm {proj}_{M}[K; x]=\operatorname {argmin}_{z \in K}\frac{1}{2}(z-x)^{T}M(z-x)$. The following equivalences are useful. Let $x \in \mathbb {R}^{n}$, $q \in \mathbb {R}^{n}$, $M \in \mathbb {R}^{n\times n}$, and $K$ be a closed convex cone. Then

$$ \begin{aligned}[b] Mx+q \in-N_{K}(x) \quad {\Leftrightarrow}\quad & K \ni x \perp Mx+q \in K^{*} \\ \quad {\Leftrightarrow}\quad &\bigl(\mbox{if}\;M=M^{T} \succeq0\bigr)\quad x= \operatorname {argmin}_{z \in K} \frac{1}{2}z^{T}Mz+q^{T}z \\ \quad {\Leftrightarrow}\quad &\bigl(\mbox{if}\;M=M^{T} \succ0\bigr)\quad x= \operatorname{proj}_{M}\bigl[K; -M ^{-1}q\bigr] \end{aligned} $$

(65)

Appendix B: Theorem 3.1.7 in [16] (excerpts)

Theorem 1

Let $M \in \mathbb {R}^{n \times n}$ be positive semidefinite, and let $q \in \mathbb {R}^{n}$ be arbitrary. The following statements hold:

• (a) If $z^{1}$ and $z^{2}$ are two solutions of the $\mathrm{LCP}(M,q)$, then $(z^{1})^{T}(q+Mz^{2})=(z^{2})^{T}(q+Mz^{1})$.

• (d) If $M$ is symmetric (and positive semidefinite), then $Mz^{1}=Mz ^{2}$ for any two solutions $z^{1}$ and $z^{2}$.

Appendix C: Theorem 3.8.6 in [16]

Theorem 2

Let $M \in \mathbb {R}^{n \times n}$ be copositive, and let $q \in \mathbb {R}^{n}$ be given. If the implication $[0 \leq v \perp Mv \geq0] \Rightarrow [v^{T}q \geq0]$ is valid, then the $\mathrm{LCP}(M,q)$ is solvable.

Let ${\mathcal{Q}}_{M}$ denote the solution set of the homogeneous LCP. This theorem can be restated equivalently as follows: If $M$ is copositive and $q \in{\mathcal{Q}}_{M}^{*}$, then $\mathrm{LCP}(M,q)$ is solvable.

Appendix D: Theorems 2.8 and 2.11 in [14]

Chen and Xiang [14] stated very useful criteria that guarantee that a positive definite or a P-matrix remains positive definite or P when it is subject to a small enough perturbation. We give here just an excerpt of the results in [14] and a corollary of it.

Theorem 3

If $M$ is a P-matrix, then all matrices $A$ such that $\beta_{2}(M) \lVert M-A \rVert_{2}<1$ are P-matrices, where $\beta_{2}(M):= \max_{d\in[0,1]^{n}} \lVert(I-D+DM)^{-1}D \rVert_{2}$, and $D=\operatorname{diag}(d)$. When $M$ is symmetric positive definite, $\beta_{2}(M)= \lVert M^{-1} \rVert_{2}$.

Theorem 4

Let $M \in \mathbb {R}^{n \times n}$ be a positive definite matrix. Then every matrix $A \in\{A \mid \vert \vert ( \frac{M+M^{T}}{2} ) ^{-1} \vert \vert _{2} \|M-A\|_{2} < 1 \}$ is positive definite.

The next corollary is proved in [10, Corollary 2].

Corollary 3

Let $A=B+C$, where $A$, $B$ and $C$ are $n \times n$ real matrices, and $B \succ0$, not necessarily symmetric. If $\|C\|_{2} < \frac{1}{\| ( \frac{B+B^{T}}{2} ) ^{-1}\|_{2}}$, then $A \succ0$.

Appendix E: KKT system: solvability and solution uniqueness

The KKT problem in (4) is ubiquitous in the study of mechanical systems with bilateral holonomic constraints. In this section, we analyze it from various points of view and we prove that it possesses some subtleties depending on which assumptions are made on the data. Let us consider the next three problems, where $M=M^{T} \in \mathbb {R}^{n \times n}$ and $M \succeq0$, $F \in \mathbb {R}^{n \times m}$, $N \in \mathbb {R}^{n \times m}$, $x \in \mathbb {R}^{n}$, $y \in \mathbb {R}^{m}$, $z \in \mathbb {R}^{n}$, $a \in \mathbb {R}^{n}$, $b \in \mathbb {R}^{m}$:

$$ \underbrace{\left ( \textstyle\begin{array}{c@{\quad}c} M & I \\ F^{T} & 0 \end{array}\displaystyle \right ) }_{\stackrel{\Delta}{=} \tilde{A} \in \mathbb {R}^{(n+m)\times2n}} \left ( \textstyle\begin{array}{c} x \\ z \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c} a \\ b \end{array}\displaystyle \right ) , $$

(66)

$$ \underbrace{\left ( \textstyle\begin{array}{c@{\quad}c} M & -F \\ F^{T} & 0 \end{array}\displaystyle \right ) }_{\stackrel{\Delta}{=} \bar{A} \in \mathbb {R}^{(n+m)\times(n+m)}} \left ( \textstyle\begin{array}{c} x \\ y \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c} a \\ b \end{array}\displaystyle \right ) , $$

(67)

and

$$ \underbrace{\left ( \textstyle\begin{array}{c@{\quad}c} M & N \\ F^{T} & 0 \end{array}\displaystyle \right ) }_{\stackrel{\Delta}{=} \hat{A} \in \mathbb {R}^{(n+m)\times(n+m)}} \left ( \textstyle\begin{array}{c} x \\ y \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c} a \\ b \end{array}\displaystyle \right ) . $$

(68)

The three systems (66), (67), and (68) correspond to various ways to consider the system in (4), where $x$ is for $\ddot{q}$, $z$ is for $-\nabla h_{\mathrm{n},b}(q)\lambda_{\mathrm{n},b}$, and $y$ is for $\lambda_{\mathrm{n},b}$.

• (i) Let us first consider (66) without any assumption on the form of $z$. From [6, Fact 2.10.22] we have $\operatorname{Im}( \tilde{A})=\operatorname{Im}\bigl( {\scriptsize\begin{matrix}{} M \cr F^{T} \end{matrix}} \bigr) +\operatorname{Im}\bigl( {\scriptsize\begin{matrix}{} I \cr 0 \end{matrix}} \bigr)$. Thus, a necessary and sufficient condition for (66) to possess a solution $(x, z)$ for any $a$ and $b$, equivalently, $\operatorname{rank}( \tilde{A})=n+m$ (which also follows from [6, Proposition 6.1.7(iii)]), is that $F^{T}$ has full rank $m$, that is, $F$ is of full column rank (this implies that $n \geq m$). The uniqueness of $(x, z)$ for any $a$ and $b$ holds if and only if $n=m$ and $\mathrm{rank}(\tilde{A})=2n$ (this may be proved from [6, Theorem 2.6.3(ii)]), in which case, $F$ is square and has full rank $n$. In this case, the solution is equal to $\tilde{A}^{\dagger}\bigl( {\scriptsize\begin{matrix}{} a \cr b \end{matrix}} \bigr)$, where $\tilde{A}^{\dagger}$ is the Moore–Penrose generalized inverse of $\tilde{A}$ [6, Proposition 6.1.7(viii)]. We see that $M$ plays no role in this system.

• (ii) Let us still consider (66) assuming that $z=-Fy$ for some $y$, that is, $z \in\operatorname{Im}(F)$. We have $(x,z) \in{ \mathrm {Ker}}( \tilde{A}) \Leftrightarrow Mx=-z$ and $x \in{ \mathrm {Ker}}(F^{T})$. Using $z \in\operatorname{Im}(F)$ and $x \in{ \mathrm {Ker}}(F^{T})$ and [6, Theorem 2.4.3], it follows that $x \perp z$. We also have $z \in\operatorname{Im}(M)$. Using that $\operatorname{Im}^{\perp}(M)={\mathrm {Ker}}(M)$, we deduce that $x \in{ \mathrm {Ker}}(M)$ because $M$ is symmetric positive semidefinite.¹³ Thus, $x \in{ \mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})$, and consequently $z=-Mx=0$. Thus, we have shown that $[(x,z) \in{ \mathrm {Ker}}(\tilde{A}) \mbox{ and } z \in\operatorname{Im}(F)] \Rightarrow[z=0\mbox{ and }x \in{ \mathrm {Ker}}(M) \cap {\mathrm {Ker}}(F^{T})]$, and the reverse implication also holds. Let $S=\{(x, z) \in \mathbb {R}^{2n} \mid z \in\operatorname{Im}(F)\}$. Then $\mathrm {Ker}( \tilde{A}) \cap S=\{(x, z) \in \mathbb {R}^{2n} \mid z=0\;\mbox{and}\;x \in {\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})\}$. We infer that ${\mathrm {Ker}}(M) \cap {\mathrm {Ker}}(F^{T})=\{0\} \Rightarrow \mathrm {Ker}(\tilde{A}) \cap S=\{0\}$. From (i) existence of solutions for system (66) holds for any $a$ and $b$ if and only if $\operatorname{rank}(\tilde{A})=n+m \Leftrightarrow\operatorname{rank}(F)=m$, hence $\operatorname{dim}(\mathrm {Ker}(\tilde{A}))=2n-n-m=n-m$. From the fact that $0 \leq\operatorname{dim}(\mathrm {Ker}(\tilde{A}) \cap S) \leq\min(n-m,n+m)=n-m$ [6, Fact 2.9.14], one infers that ${\mathrm {Ker}}(M) \cap {\mathrm {Ker}}(F^{T})=\{0\} \Rightarrow\operatorname{dim}(\mathrm {Ker}(\tilde{A}) \cap S)=0$, thus $n=m$. In this case it follows from (i) that the system has a unique solution for any $a$ and $b$. Conversely the existence of solutions for arbitrary $a$ and $b$ and $n=m$ imply uniqueness, as well as ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})=\{0\}$ since $F$ is square full rank $n$.

Let us now pass to the system (67). Remark that if $\bar{A}$ in (67) is invertible then $F$ necessarily has full rank $m$. This follows from the fact that $(x,y) \in \mathrm {Ker}(\bar{A})$ implies $x \in \mathrm {Ker}(M) \cap \mathrm {Ker}(F^{T})$ and $y \in \mathrm {Ker}(F)$, using similar arguments as in (ii). In particular, if there are more constraints than degrees of freedom (i.e., $m>n$), then $\bar{A}$ is not invertible, and likewise if $\mathrm{rank}(F)=r< m$.

• (iii) Consider now system (67). Let $\operatorname{rank}(F)=m$ (so $m\le n$), and $M$ be positive semidefinite. Then the existence and uniqueness of both $x$ and $y$ for arbitrary $a$ and $b$ (equivalently, nonsingularity of $\bar{A}$) holds if and only if ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})=\{0\}$ (proof by direct application of [8, p. 523] or by using the above expression of $\mathrm {Ker}(\bar{A})$).

The rank condition on $F$ appears to be in fact necessary and sufficient as alluded to few lines above:

• (iii′) System (67) has a unique solution $(x,y)$ for arbitrary $a$ and $b$ if and only if $\operatorname{rank}(F)=m$ and ${\mathrm {Ker}}(M) \cap {\mathrm {Ker}}(F^{T})=\{0\}$. This solution is equal to $\bar{A}^{-1}\bigl( {\scriptsize\begin{matrix}{} a \cr b \end{matrix}} \bigr)$.

The proof of (iii′) follows from [6, Theorem 2.6.3, Proposition 6.1.7], noting that $\bar{A}$ is square. It is sometimes wrongly stated that $\bar{A}$ is nonsingular if and only if $M$ and $F$ are both full-rank matrices [34], which is only a sufficient condition. In fact, from [6, Fact 6.4.20] we have:

$$ \begin{aligned}[b] \operatorname{rank}(\bar{A}) &= \operatorname{rank}(M)+2\operatorname{rank}(F)- \operatorname{dim}\bigl[\operatorname{Im}(M) \cap\operatorname{Im}(F)\bigr] \\ &\quad {}-\operatorname{dim}\biggl[\operatorname{Im} \left ( \textstyle\begin{array}{c} M \\ F^{T} \end{array}\displaystyle \right ) \cap\operatorname{Im} \left ( \textstyle\begin{array}{c} F \\ 0 \end{array}\displaystyle \right ) \biggr]. \end{aligned} $$

(69)

Formula (69) shows that we may dispense with positive definiteness conditions on $M$ and that the nonsingularity of $\bar{A}$ results from an interplay between the matrices ranges. Consider, for instance, $M=\bigl( {\scriptsize\begin{matrix}{} 1 & 0 \cr 0 & -1 \end{matrix}} \bigr)$ and $F=(1\;0)^{T}$, which yields $\operatorname{rank}(\bar{A})=3$. In contact mechanics, we wish to allow for situations where the constraints are redundant, so that ($\operatorname{rank}(F)=r< \min(m,n)$), but which are nevertheless compatible (i.e., $b\in\operatorname{Im}(F^{T})$) since otherwise the problem has no solution. Thus, the most relevant problem is that of determining $x$ and $y$ such that (67) holds for arbitrary $a$ with the additional assumption that $b\in\operatorname{Im}(F^{T})$. This problem is thus different from problems tackled in (ii) and (iii′) and corresponds to the problem tackled in [30, 31, 59].

• (iv) The necessary and sufficient condition for the existence of $x$ and $y$ with uniqueness of $x$ and $Fy$ such that (67) holds for arbitrary $a$ is that $b\in\operatorname{Im}(F^{T})$ and ${\mathrm {Ker}}(M) \cap {\mathrm {Ker}}(F^{T})=\{0\}$.

Proof

⇐

Existence of $x$ and $y$ : By contraposition, if not ($\forall a, \exists x \mbox{ and }y$ such that (67) holds), then there exists $a\in \mathbb {R}^{n}$ such that for all $x,y$, $F^{T}x \neq b$ (so $b\notin\operatorname{Im}(F^{T})$) or $Mx-Fy\neq a$ (so $\operatorname{Im}([M\;F])\neq \mathbb {R}^{n}$, that is, ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F ^{T})\neq\{0\}$.

Uniqueness of $x$ and $Fy$ : Suppose that $b\in\operatorname{Im}(F^{T})$ and ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})=\{0\}$.

If $(x_{1},y_{1})$ and $(x_{2},y_{2})$ are two solutions of (67), then $F^{T}(x_{1}-x_{2})=0$ and $M(x_{1}-x_{2})=F(y_{1}-y _{2})$. Hence, $(x_{1}-x_{2})\in{ \mathrm {Ker}}(F^{T})$ and $M(x_{1}-x_{2}) \in\operatorname{Im}(F)={\mathrm {Ker}}(F^{T})^{\bot}$. Hence, $(x_{1}-x_{2})^{T}M(x _{1}-x_{2})=0$, and since $M$ is symmetric positive semidefinite, this means $(x_{1}-x_{2})\in{ \mathrm {Ker}}(M)$. By hypothesis, ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})=\{0\}$, so we conclude that $x_{1}-x_{2}=0$, that is, $x$ is unique. It follows that $Fy_{1}=Fy_{2}$, so that $Fy$ is unique as well.

⇒

Suppose that for arbitrary $a$, there exist $x$ and $y$ such that (67) holds with uniqueness of $x$ and $Fy$. Then, in particular, $b\in\operatorname{Im}(F^{T})$. Let $x \in{ \mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})$, and let $(x^{\star}, y)$ be the unique solution of (67). Then $(x^{\star}+x, y)$ is also a solution of (67). Hence, $x=0$, so that ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})={0}$. □

In [31, p. 319], the condition $b\in\operatorname{Im}(F^{T})$ is stated as follows: acceleration constraints are compatible. In conclusion, four types of systems are considered: system (67) with unknowns $x$ and $y$ in (iii), system (66) with unknowns $x$ and $z$ in (i), system (66) with unknowns $x$ and $z$ and the constraints that $z \in\operatorname{Im}(F)$ in (ii), system (67) with unknowns $x$ and $y$ with uniqueness of $x$ and $Fy$ and arbitrary $a$ in (iv). To complete the picture, let us note that ${\mathrm {Ker}}(M) \cap{ \mathrm {Ker}}(F^{T})=\{0\} \Leftrightarrow(\operatorname{Im}(M)+\operatorname{Im}(F))=\mathbb {R}^{n} \Leftrightarrow\operatorname{Im}[(M\;F)]=\mathbb {R}^{n}$ using [6, Fact 2.9.10], and we recover directly an alternative way to formulate the condition involving the kernels, sometimes used in the literature [59] [30, Eq. (9)].

Problems like in (67) and (66) occur in frictionless systems. The next step is to consider systems of the form (68) for some matrix $N$. Such problems arise in the presence of Coulomb’s friction; see (36). Using [6, Fact 6.4.20], we get an extension of (69):

$$ \begin{aligned}[b] \operatorname{rank}(\hat{A}) & = \operatorname{rank}(M)+\operatorname{rank} \bigl(F^{T}\bigr)+\operatorname{rank}(N)- \operatorname{dim}\bigl[ \operatorname{Im}(M)\cap\operatorname{Im}(F)\bigr] \\ &\quad {}-\operatorname{dim}\biggl[ \operatorname{Im} \left ( \textstyle\begin{array}{c} M \\ F^{T} \end{array}\displaystyle \right ) \cap \operatorname{Im} \left ( \textstyle\begin{array}{c} N \\ 0 \end{array}\displaystyle \right ) \biggr]. \end{aligned} $$

(70)

System (68) has a unique solution $(x, y)$ for any $a$ and $b$ if and only if $\operatorname{rank}(\hat{A})=n+m$. We have:

$$ \begin{aligned}[b] & \operatorname{Im} \left ( \textstyle\begin{array}{c} M \\ F^{T} \end{array}\displaystyle \right ) \cap \operatorname{Im} \left ( \textstyle\begin{array}{c} N \\ 0 \end{array}\displaystyle \right ) \\ &\quad = \biggl\{ z \in \mathbb {R}^{n+m} \Bigm| \exists\;y_{1} \in \mathrm {Ker}\bigl(F^{T} \bigr), \exists\;y_{2} \in \mathbb {R}^{m} \mbox{such that}\; z= \left ( \textstyle\begin{array}{c} My_{1} \\ 0 \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c} Ny_{2} \\ 0 \end{array}\displaystyle \right ) \biggr\} \end{aligned} $$

(71)

and $\operatorname{Im}(M)\cap\operatorname{Im}(F)= \{z \in \mathbb {R}^{n} \mid \exists\;y_{1} \in \mathbb {R}^{n}, \exists\;y_{2}\in \mathbb {R}^{m} \mbox{such that}\;z=My_{1}=Fy _{2}\}$. It is clear from (70) that the well-posedness of a system depends on the interplay between $M$, $F$, and $N$. Even if all three matrices have full rank, then we may have $\operatorname{rank}(\hat{A}) < n+m$. Suppose that $\operatorname{rank}(M)=n$, and $\operatorname{rank}(F^{T}M^{-1}N)=m$ (implying that $m\leq n$). Then $\operatorname{Im}(M)\cap\operatorname{Im}(F)=\operatorname{Im}(F)$ and $\operatorname{Im}\bigl( {\scriptsize\begin{matrix}{} M \cr F^{T} \end{matrix}} \bigr) \cap\operatorname{Im}\bigl( {\scriptsize\begin{matrix}{} N \cr 0 \end{matrix}} \bigr) =\{0\}$ (since $F^{T}y_{1}=0=F^{T}M^{-1}Ny_{2}$). Therefore, from (70) we have $\operatorname{rank}(\hat{A})=n+m$.

Finally, we may rewrite (68) as (66) posing $z=Ny$. Then (i) applies, but (ii) usually is not except if $\operatorname{Im}(N) \subseteq \operatorname{Im}(F)$. Then given $z$, there exists a unique $y$ if and only if $N$ has full column rank $m$ ($\Rightarrow m \leq n$). Let $N=-F + P$ for some matrix $P$.

• (v) Assume that $F$ has full column rank $m$ (equivalently, $F^{T}F \in \mathbb {R}^{m \times m}$ is positive definite). Let us investigate conditions that guarantee that $N$ has full rank $m$ (equivalently, $N^{T}N \in \mathbb {R}^{m \times m}$ is positive definite). We have $N^{T}N=F^{T}F-F^{T}P-P^{T}F+P^{T}P$. A direct application of Corollary 3, with matrices $A,B,C$ chosen as $A=N^{T}N$, $B=F^{T}F$ and $C=-F^{T}P-P^{T}F+P^{T}P$, shows that a sufficient condition for $N^{T}N$ to be positive definite is that $\|-F^{T}P-P ^{T}F+P^{T}P\|_{2} < \frac{1}{\|(F^{T}F)^{-1}\|_{2}}$ or, equivalently, $\sigma_{\max}(-F^{T}P-P^{T}F+P^{T}P) < \sigma_{\min}(F^{T}F)$.

Let $M=0$. Then, using (70), it follows that $\operatorname{rank}( \hat{A})=2m$; hence, $\operatorname{rank}(\hat{A})=n+m$ if and only if $n=m$. This shows that, depending on the interplay between the ranges of the matrices in (70), system (68) may be solvable with uniqueness for any $a$ and $b$, for low-rank matrices $M$.

• (vi) Let us assume that $\operatorname{rank}(M)=n$ and study conditions such that the rank of $F^{T}M^{-1}N=-F^{T}M^{-1}F+F^{T}M^{-1}P$ is $m$. Then, as shown after (71), $\hat{A}$ has rank $n+m$, and system (68) has a unique solution for any $a$ and $b$. Using Corollary 3 with matrices $A,B,C$ chosen as $A=-F^{T}M^{-1}N$, $B=F^{T}M^{-1}F$ and $C=-F^{T}M^{-1}P$, we conclude that $\operatorname{rank}(F ^{T}M^{-1}N)=m$ if $\operatorname{rank}(F)=m$ and $\sigma_{\max}(-F^{T}M^{-1}P) < \sigma_{\min}(F^{T}M^{-1}F)$.

It is worth noting that the study of problem (68) may also be quite useful in the context of numerical analysis of differential algebraic equations (DAEs). Half-explicit methods involve such problems (for instance, $N$ may be the Jacobian of the constraints estimated at step $i+1$, whereas $F$ is the Jacobian estimated at step $i$) [56, §7.1], [24, §VII.6]; see also [13, 39, 45, 46] for various forms of numerical KKT systems.