Skip to main content
SpringerLink
Log in

Co-simulation method for solver coupling with algebraic constraints incorporating relaxation techniques

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

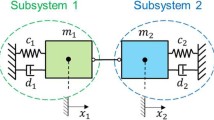
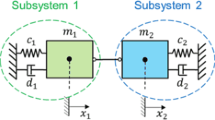
Abstract

Based on the stabilized index-2 formulation for multibody systems, a semi-implicit co-simulation approach for solver coupling with algebraic constraints has been presented by Schweizer and Lu (Multibody Syst. Dyn., 2014) for the case that constant approximation is used for extrapolating/interpolating the coupling variables. In the manuscript at hand, this method is generalized to the case that higher-order approximation is employed. Direct application of higher-order polynomials for extrapolating/interpolating the coupling variables fails. Using linear approximation polynomials, artificial oscillations in the Lagrange multipliers of the kinematical differential equations are observed. For quadratic and higher-order polynomials, the co-simulation becomes unstable. In this work, the key idea to obtain stable solutions without artificial oscillations is to apply a relaxation technique. A detailed stability and convergence analysis is presented in the paper for the case of higher-order approximation. In this context, the influence of the relaxation parameter on the stability and convergence behavior is investigated. Applicability and robustness of the stabilized index-2 co-simulation method incorporating higher-order approximation polynomials is demonstrated with different numerical examples. Using piecewise constant approximation polynomials for the coupling variables produces discontinuous accelerations and reaction forces in the subsystems at the macrotime points, which may entail problems for the subsystem integrator. With higher-order approximation polynomials, the coupling variables and in consequence the accelerations and reaction forces in the subsystems become continuous.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Ambrosio, J., Pombo, J., Rauter, F., Pereira, M.: A memory based communication in the co-simulation of multibody and finite element codes for pantograph-catenary interaction simulation. In: Bottasso, C.L. (ed.) Multibody Dynamics: Computational Methods and Applications, pp. 231–252. Springer, Berlin (2009)

    Google Scholar 

  2. Ambrosio, J., Pombo, J., Pereira, M., Antunes, P., Mosca, A.: A computational procedure for the dynamic analysis of the catenary-pantograph interaction in high-speed trains. J. Theor. Appl. Mech. 50(3), 681–699 (2012)

    Google Scholar 

  3. Anderson, K.S.: An order-\(n\) formulation for the motion simulation of general multi-rigid-body tree systems. Comput. Struct. 46(3), 547–559 (1993)

    Article  MATH  Google Scholar 

  4. Anderson, K., Duan, S.: A hybrid parallelizable low-order algorithm for dynamics of multi-rigid-body systems: Part I, Chain systems. Math. Comput. Model. 30(9–10), 193–215 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  5. Arnold, M.: Numerical methods for simulation in applied dynamics. In: Arnold, M., Schiehlen, W. (eds.) Simulation Techniques for Applied Dynamics. Springer, Berlin (2009)

    Chapter  Google Scholar 

  6. Arnold, M., Clauss, C., Schierz, T.: Error analysis and error estimates for co-simulation in FMI for model exchange and co-simulation in V2.0. Arch. Mech. Eng. 60(1), 75–94 (2013)

    Google Scholar 

  7. Busch, M., Schweizer, B.: Numerical stability and accuracy of different co-simulation techniques: Analytical investigations based on a 2-DOF test model. In: Proceedings of the 1st Joint International Conference on Multibody System Dynamics, IMSD 2010, Lappeenranta, Finland, 25–27 May (2010)

    Google Scholar 

  8. Busch, M., Schweizer, B.: An explicit approach for controlling the macro-step size of co-simulation methods. In: Proceedings of the 7th European Nonlinear Dynamics, ENOC 2011, Rome, Italy, 24–29 July (2011)

    Google Scholar 

  9. Busch, M., Schweizer, B.: Coupled simulation of multibody and finite element systems: an efficient and robust semi-implicit coupling approach. Arch. Appl. Mech. 82(6), 723–741 (2012)

    Article  MATH  Google Scholar 

  10. Carstens, V., Kemme, R., Schmitt, S.: Coupled simulation of flow-structure interaction in turbomachinery. Aerosp. Sci. Technol. 7, 298–306 (2003)

    Article  MATH  Google Scholar 

  11. Cuadrado, J., Cardenal, J., Morer, P., Bayo, E.: Intelligent simulation of multibody dynamics: Space-state and descriptor methods in sequential and parallel computing environments. Multibody Syst. Dyn. 4, 55–73 (2000)

    Article  MATH  Google Scholar 

  12. Daniel, W.J.T.: Analysis and implementation of a new constant acceleration subcycling algorithm. Int. J. Numer. Methods Eng. 40, 2841–2855 (1997)

    Article  MATH  Google Scholar 

  13. Daniel, W.J.T.: A study of the stability of subcycling algorithms in structural dynamics. Comput. Methods Appl. Mech. Eng. 156, 1–13 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  14. Daniel, W.J.T.: A partial velocity approach to subcycling structural dynamics. Comput. Methods Appl. Mech. Eng. 192, 375–394 (2003)

    Article  MATH  Google Scholar 

  15. Datar, M., Stanciulescu, I., Negrut, D.: A co-simulation framework for full vehicle analysis. In: Proceedings of the SAE 2011 World Congress, SAE Technical Paper 2011-01-0516, 12–14 April, Detroit, Michigan, USA (2011).

    Google Scholar 

  16. Datar, M., Stanciulescu, I., Negrut, D.: A co-simulation environment for high-fidelity virtual prototyping of vehicle systems. Int. J. Veh. Syst. Model. Test. 7, 54–72 (2012)

    Article  Google Scholar 

  17. Dörfel, M.R., Simeon, B.: Analysis and acceleration of a fluid-structure interaction coupling scheme. Numer. Math. Adv. Appl., 307–315 (2010)

  18. Eberhard, P., Gaugele, T., Heisel, U., Storchak, M.: A discrete element material model used in a co-simulated Charpy impact test and for heat transfer. In: Proceedings 1st Int. Conference on Process Machine Interactions, Hannover, Germany, 3–4 September (2008)

    Google Scholar 

  19. Eich, E.: Convergence results for a coordinate projection method applied to mechanical systems with algebraic constraints. SIAM J. Numer. Anal. 30(5), 1467–1482 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  20. Eich-Soellner, E., Führer, C.: Numerical Methods in Multibody Dynamics. Teubner, Stuttgart (1998)

    Book  MATH  Google Scholar 

  21. Friedrich, M., Ulbrich, H.: A parallel co-simulation for mechatronic systems. In: Proceedings of the 1st Joint International Conference on Multibody System Dynamics, IMSD 2010, Lappeenranta, Finland, 25–27 May (2010)

    Google Scholar 

  22. Gear, C.W., Gupta, G.K., Leimkuhler, B.J.: Automatic integration of the Euler-Lagrange equations with constraints. J. Comput. Appl. Math. 12&13, 77–90 (1985)

    Article  MathSciNet  Google Scholar 

  23. Gonzalez, F., Gonzalez, M., Cuadrado, J.: Weak coupling of multibody dynamics and block diagram simulation tools. In: Proceedings of the ASME 2009 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, IDETC/CIE 2009, San Diego, California, USA, August 30–September 2 (2009)

    Google Scholar 

  24. Gonzalez, F., Naya, M.A., Luaces, A., Gonzalez, M.: On the effect of multirate co-simulation techniques in the efficiency and accuracy of multibody system dynamics. Multibody Syst. Dyn. 25(4), 461–483 (2011)

    Article  MATH  Google Scholar 

  25. Gu, B., Asada, H.H.: Co-simulation of algebraically coupled dynamic subsystems without disclosure of proprietary subsystem models. J. Dyn. Syst. Meas. Control 126, 1–13 (2004)

    Article  Google Scholar 

  26. Hairer, E., Norsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I: Nonstiff Problems, 3rd edn. Springer, Berlin (2009)

    Google Scholar 

  27. Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 2nd edn. Springer, Berlin (2010)

    Google Scholar 

  28. Haug, E.J.: Computer-Aided Kinematics and Dynamics of Mechanical Systems. Allyn and Bacon, Needhom Heights (1989)

    Google Scholar 

  29. Hippmann, G., Arnold, M., Schittenhelm, M.: Efficient simulation of bush and roller chain drives. In: Proceedings of ECCOMAS Thematic Conference on Multibody Dynamics, Madrid, Spain, 21–24 June (2005)

    Google Scholar 

  30. Kübler, R., Schiehlen, W.: Two methods of simulator coupling. Math. Comput. Model. Dyn. Syst. 6, 93–113 (2000)

    Article  MATH  Google Scholar 

  31. Kübler, R., Schiehlen, W.: Modular simulation in multibody system dynamics. Multibody Syst. Dyn. 4, 107–127 (2000)

    Article  MATH  Google Scholar 

  32. Lacoursiere, C., Nordfeldth, F., Linde, M.: A partitioning method for parallelization of large systems in realtime. In: Proceedings of the 3rd Joint International Conference on Multibody System Dynamics and the 7th Asian Conference on Multibody Dynamics, IMSD 2014, ACMD 2014, Bexco, Busan, Korea, June 30–July 3 (2014)

    Google Scholar 

  33. Laflin, J.J., Anderson, K.S., Khan, I.M., Poursina, M.: Advances in the application of the divide-and-conquer algorithm to multibody system dynamics. J. Comput. Nonlinear Dyn., 9 (2014). doi:10.1115/1.4026072

  34. Lehnart, A., Fleissner, F., Eberhard, P.: Using SPH in a co-simulation approach to simulate sloshing in tank vehicles. In: Proceedings SPHERIC4, Nantes, France, 27–29 May (2009)

    Google Scholar 

  35. Liao, Y.G., Du, H.I.: Co-simulation of multi-body-based vehicle dynamics and an electric power steering control system. Proc. Inst. Mech. Eng. K, J. Multibody Dyn. 215, 141–151 (2001)

    Article  Google Scholar 

  36. Lubich, Ch.: Extrapolation integrators for constraint multibody systems. Impact Comput. Sci. Eng. 3, 213–234 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  37. Malczyk, P., Fraczek, J.: Evaluation of parallel efficiency in modeling of mechanisms using commercial multibody solvers. Arch. Mech. Eng. LVI(3), 237–249 (2009)

    Google Scholar 

  38. Meynen, S., Mayer, J., Schäfer, M.: Coupling algorithms for the numerical simulation of fluid-structure-interaction problems. In: ECCOMAS 2000: European Congress on Computational Methods in Applied Sciences and Engineering, Barcelona (2000)

    Google Scholar 

  39. Mraz, L., Valasek, M.: Parallelization of multibody system dynamics by additional dynamics. In: Proceedings of the ECCOMAS Thematic Conference Multibody Dynamics 2013, Zagreb, Croatia, 1–4 July (2013)

    Google Scholar 

  40. Naya, M., Cuadrado, J., Dopico, D., Lugris, U.: An efficient unified method for the combined simulation of multibody and hydraulic dynamics: Comparison with simplified and co-integration approaches. Arch. Mech. Eng. LVIII, 223–243 (2011)

    Article  Google Scholar 

  41. Negrut, N., Melanz, D., Mazhar, H., Lamb, D., Jayakumar, P.: Investigating through simulation the mobility of light tracked vehicles operating on discrete granular terrain. SAE Int. J. Passeng. Cars, Mech. Syst. 6, 369–381 (2013). doi:10.4271/2013-01-1191

    Article  Google Scholar 

  42. Pombo, J., Ambrosio, J.: Multiple pantograph interaction with catenaries in high-speed trains. J. Comput. Nonlinear Dyn. 7(4), 041008 (2012)

    Article  Google Scholar 

  43. Schäfer, M., Yigit, S., Heck, M.: Implicit partitioned fluid-structure interaction coupling. In: ASME, PVP2006-ICPVT11-93184, Vancouver, Canada (2006)

    Google Scholar 

  44. Schiehlen, W.: Multibody system dynamics: roots and perspectives. Multibody Syst. Dyn. 1, 149–188 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  45. Simeon, B.: Computational Flexible Multibody Dynamics: A Differential-Algebraic Approach. Springer, Berlin (2013)

    Book  Google Scholar 

  46. Schmoll, R., Schweizer, B.: Co-simulation of multibody and hydraulic systems: comparison of different coupling approaches. In: Proceedings of ECCOMAS Thematic Conference on Multibody Dynamics 2011, Brussels, Belgium, 4–7 July (2011)

    Google Scholar 

  47. Schweizer, B., Lu, D.: Predictor/corrector co-simulation approaches for solver coupling with algebraic constraints. ZAMM—J. Appl. Math. Mech. (2014). doi:10.1002/zamm.201300191

    Google Scholar 

  48. Schweizer, B., Lu, D.: Co-simulation methods for solver coupling with algebraic constraints: Semi-implicit coupling techniques. In: Proceedings of the 3rd Joint International Conference on Multibody System Dynamics and the 7th Asian Conference on Multibody Dynamics, IMSD 2014, ACMD 2014 Bexco, Busan, Korea, June 30–July 3 (2014)

    Google Scholar 

  49. Schweizer, B., Lu, D.: Stabilized index-2 co-simulation approach for solver coupling with algebraic constraints. Multibody Syst. Dyn. (2014). doi:10.1007/s11044-014-9422-y

    Google Scholar 

  50. Schweizer, B., Lu, D.: Semi-implicit co-simulation approach for solver coupling. Arch. Appl. Mech. (2014). doi:10.1007/s00419-014-0883-5

    Google Scholar 

  51. Schweizer, B., Li, P., Lu, D.: Explicit and implicit co-simulation methods: Stability and convergence analysis for different solver coupling approaches. J. Comput. Nonlinear Dyn. (2014). doi:10.1115/1.4028503

    Google Scholar 

  52. Schweizer, B., Li, P., Lu, D., Meyer, T.: Stabilized implicit co-simulation methods: Solver coupling based on constitutive laws. Arch. Appl. Mech. (2015). doi:10.1007/s00419-015-0999-2

    Google Scholar 

  53. Schweizer, B., Li, P., Lu, D., Meyer, T.: Stabilized implicit co-simulation method: Solver coupling with algebraic constraints for multibody systems. J. Comput. Nonlinear Dyn. (2015). doi:10.1115/1.4030508

    Google Scholar 

  54. Schweizer, B., Li, P., Lu, D.: Implicit co-simulation methods: stability and convergence analysis for solver coupling with algebraic constraints. ZAMM—J. Appl. Math. Mech. (2015). doi:10.1002/zamm.201400087

    Google Scholar 

  55. Spreng, F., Eberhard, P., Fleissner, F.: An approach for the coupled simulation of machining processes using multibody system and smoothed particle hydrodynamics algorithms. Theor. Appl. Mech. Lett. 3(1), 8–013005 (2013)

    Article  Google Scholar 

  56. Tomulik, P., Fraczek, J.: Simulation of multibody systems with the use of coupling techniques: a case study. Multibody Syst. Dyn. 25(2), 145–165 (2011)

    Article  MathSciNet  Google Scholar 

  57. Verhoeven, A., Tasic, B., Beelen, T.G.J., ter Maten, E.J.W., Mattheij, R.M.M.: BDF compound-fast multirate transient analysis with adaptive stepsize control. J. Numer. Anal. Ind. Appl. Math. 3(3–4), 275–297 (2008)

    MATH  Google Scholar 

  58. Zierath, J., Woernle, C.: Development of a Dirichlet-to-Neumann algorithm for contact analysis in boundary element systems and its application to MBS-BEM co-simulation. In: Samin, J.C., Fisette, P. (eds.) MULTIBODY DYNAMICS 2011, ECCOMAS Thematic Conference, Brussels, Belgium, 4–7 July (2011)

    Google Scholar 

  59. Zierath, J., Woernle, C.: Contact modelling in multibody systems by means of a boundary element co-simulation and a Dirichlet-to-Neumann algorithm. In: Oñate, E. (Series ed.) Computational Methods in Applied Sciences. Springer, Berlin (2012)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Institute of Applied Dynamics, Technical University Darmstadt, Otto-Berndt-Strasse 2, 64287, Darmstadt, Germany

    Bernhard Schweizer, Daixing Lu & Pu Li

Authors
  1. Bernhard Schweizer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Daixing Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bernhard Schweizer.

Appendices

Appendix A: Stability plots

1.1 A.1 Stability plots: relaxation parameter \(\omega_{R} =1\)

Fig. 15
figure 15

Stability plots for the stabilized index-2 co-simulation method: Relaxation parameter \({\omega}_{R} =1\), polynomial degrees \(k=0,1,2\)

Full size image

1.2 A.2 Stability plots: relaxation parameter \(\omega_{R} =0.7\)

Fig. 16
figure 16

Stability plots for the stabilized index-2 co-simulation method: Relaxation parameter \({\omega}_{R} =0.7\), polynomial degrees \({k}=0,1,2\)

Full size image

1.3 A.3 Stability plots: relaxation parameter \(\omega_{R} =0.5\)

Fig. 17
figure 17

Stability plots for the stabilized index-2 co-simulation method: Relaxation parameter \({\omega}_{R} =0.5\), polynomial degrees \({k}=0,1,2\)

Full size image

Appendix B: Convergence plots

Fig. 18
figure 18

Convergence plots for the stabilized index-2 co-simulation method (local and global errors of the position and velocity variables): Relaxation parameters \({\omega}_{R} =1\), \(\omega_{R} =0.7\), \(\omega_{R}=0.5\); polynomial degrees \({k}=0,1,2\)

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schweizer, B., Lu, D. & Li, P. Co-simulation method for solver coupling with algebraic constraints incorporating relaxation techniques. Multibody Syst Dyn 36, 1–36 (2016). https://doi.org/10.1007/s11044-015-9464-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-015-9464-9

Keywords

Search

Navigation