Trajectory tracking and vibration suppression of a 3-PRR parallel manipulator with flexible links

Abstract

To achieve high speed, flexible planar parallel manipulators (PPM) are typically designed with lightweight linkages, but hence suffer from unwanted structural vibration, diminishing positioning accuracy. To achieve high positioning accuracy, this paper addresses the vibration suppression of a PPM with three flexible linkages actuated by linear ultrasonic motors (LUSM). Based on the extended Hamilton’s principle, a rigid–flexible dynamic model of a proposed PPM is developed using the substructure approach and the assumed mode method (AMM). The assumed mode shapes of the flexible linkages are verified through the experimental modal tests. Then, two control algorithms are designed for tracking control of the end effector and vibration attenuation of the flexible linkages. The first approach is a two-timescale control based on singular perturbation principles, implemented as a joint motion control without additional actuators. The second approach is a dual-stage control method. In this control approach, a variable structural control (VSC) method is applied to realize motion tracking of the moving platform, while the strain and strain rate feedback control (SSRF) is developed to suppress the undesired vibration of the flexible linkages, using multiple distributed collocated lead zirconate titanate (PZT) transducers. Stability analysis of the two algorithms is investigated based on Lyapunov approach. Simulation results of these two approaches show that the dual-stage control method provides better vibration attenuation, and hence, faster settling time of the PPM is achieved.

Appendix

$$\begin{aligned} M_{P} =& M_{33} = \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} m_{P} & 0 & 0 \\ 0 & m_{P} & 0 \\ 0 & 0 & J_{\phi_{p}} \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(68)

$$\begin{aligned} J_{fp} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} - 1 & 0 & - 1 & 0 & - 1 & 0 \\ 0 & - 1 & 0 & - 1 & 0 & - 1 \\ e_{1y} & - e_{1x} & e_{2y} & - e_{2x} & e_{3y} & - e_{3x} \end{array} \right] \in R^{3 \times6} \end{aligned}$$

(69)

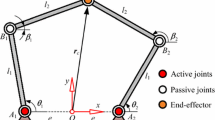
where $\bar{e}_{i} = (e_{ix},e_{iy}) = (x'_{C_{i}}\cos\phi_{P} - y'_{C_{i}}\sin \phi_{P},x'_{C_{i}}\sin\phi_{P} + y'_{C_{i}}\cos\phi_{P})$; $x'_{C_{i}}, y'_{C_{i}}$ represent the coordinates of C _i in moving coordinate frame X′PY′.

$$\begin{aligned} M =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} M_{11} & M_{12} & 0 & M_{14} \\ M_{12}^{T} & M_{22} & 0 & M_{24} \\ 0 & 0 & M_{33} & 0 \\ M_{14}^{T} & M_{24}^{T} & 0 & M_{44} \end{array} \right] \in R^{(9 + 3r) \times(9 + 3r)} \end{aligned}$$

(70)

$$\begin{aligned} M_{11} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} m_{S_1} + m_{B_1} + m_{1} & 0 & 0 \\ 0 & m_{S_2} + m_{B_2} + m_{2} & 0 \\ 0 & 0 & m_{S_3} + m_{B_3} + m_{3} \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(71)

$$\begin{aligned} M_{12} =& \left[ \begin{array}{@{}c@{\quad}c@{}} \frac{m_{1}L_{1}S_{1}}{2} - C_{1}\rho_{A_1}\sum_{j = 1}^{r} \int_{0}^{L_{1}} Y_{1j}q_{1j}\,dt & 0 \\ 0 & \frac{m_{2}L_{2}S_{2}}{2} - C_{2}\rho_{A_2}\sum_{j = 1}^{r} \int_{0}^{L_{2}} Y_{2j}q_{2j}\,dt \\ 0 & 0 \end{array}\right. \\ &\phantom{[}\quad{}\left.\begin{array}{@{}c@{}} 0\\ 0\\ \frac{m_{3}L_{3}S_{3}}{2} - C_{3}\rho_{A_3}\sum_{j = 1}^{r} \int_{0}^{L_{3}} Y_{3j}q_{3j}\,dt \end{array}\right] \in R^{3 \times3} \end{aligned}$$

(72)

$$\begin{aligned} M_{14} =& \left[\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} S_{1}\int_{0}^{L_{1}} \rho_{A_1}Y_{11}\,dx & \ldots& S_{1}\int_{0}^{L_{1}} \rho_{A_1}Y_{1r}\,dx & 0 & \ldots \\ 0 & \ldots& 0 & S_{2}\int_{0}^{L_{2}} \rho_{A_2}Y_{21}\,dx & \ldots\\ 0 & \ldots& 0 & 0 & \ldots \end{array}\right. \\ &\phantom{[}\quad{} \left.\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & \ldots& 0\\ S_{2}\int_{0}^{L_{2}} \rho_{A_2}Y_{2r}\,dx & 0 & \ldots& 0 \\ 0 & S_{3}\int_{0}^{L_{3}} \rho _{A_3}Y_{31}\,dx & \ldots& S_{3}\int_{0}^{L_{3}} \rho_{A_3}Y_{3r}\,dx \end{array}\right]\in R^{3 \times3r} \end{aligned}$$

(73)

$$\begin{aligned} M_{22} =& \left[ \begin{array}{@{}c@{\ \ }c@{}} \frac{m_{1}L_{1}^{2}}{3} + J_{B_1} + \int_{0}^{L_{1}} \rho_{A_1}(\sum_{j = 1}^{r} Y_{1j}q_{1j})^{2}\, dt & 0\\ 0 & \frac{m_{2}L_{2}^{2}}{3} + J_{B_2} + \int_{0}^{L_{2}} \rho_{A_2}(\sum_{j = 1}^{r} Y_{2j}q_{2j})^{2}\, dt \\ 0 & 0 \end{array}\right. \\ &\phantom{[}\quad{} \left.\begin{array}{@{}c@{}} 0\\ 0\\ \frac{m_{3}L_{3}^{2}}{3} + J_{B_3} + \int_{0}^{L_{3}} \rho_{A_3}(\sum_{j = 1}^{r} Y_{3j}q_{3j})^{2}\,dt \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(74)

$$\begin{aligned} M_{24} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} M_{24}^{1} & 0 & 0 \\ 0 & M_{24}^{2} & 0 \\ 0 & 0 & M_{24}^{3} \end{array} \right] \in R^{3 \times3r} \end{aligned}$$

(75)

$$\begin{aligned} M_{24}^{i} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} \int_{0}^{L_{i}} \rho_{A_i}xY_{i1}\,dx + J_{B_i}Y'_{i1}(0) & \ldots& \int_{0}^{L_{i}} \rho_{A_i}xY_{ir}\,dx + J_{B_i}Y'_{ir}(0) \end{array} \right] \in R^{1 \times r} \end{aligned}$$

(76)

$$\begin{aligned} M_{44} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} M_{44}^{1} & 0 & 0 \\ 0 & M_{44}^{2} & 0 \\ 0 & 0 & M_{44}^{3} \end{array} \right] \in R^{3r \times3r} \end{aligned}$$

(77)

$$\begin{aligned} M_{44}^{i} =& \left[\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \int_{0}^{L_{i}} \rho_{A_i}Y_{i1}^{2}\,dx + J_{B_i}Y_{i1}^{\prime 2}(0) & \ldots& 0 \\ \vdots& \ldots& \vdots\\ 0 & \ldots& \int_{0}^{L_{i}} \rho_{A_i}Y_{ir}^{2}\,dx + J_{B_i}Y_{ir}^{\prime 2}(0) \end{array} \right] \in R^{r \times r} \end{aligned}$$

(78)

$$\begin{aligned} C =& \left[\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & C_{12} & 0 & C_{14} \\ 0 & C_{22} & 0 & C_{24} \\ 0 & 0 & 0 & 0 \\ 0 & - C_{24}^{T} & 0 & 0 \end{array} \right] \in R^{(9 + 3r) \times(9 + 3r)} \end{aligned}$$

(79)

$$\begin{aligned} C_{12} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} C_{12}^{1} & 0 & 0 \\ 0 & C_{12}^{2} & 0 \\ 0 & 0 & C_{12}^{3} \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(80)

$$\begin{aligned} C_{12}^{i} =& - \frac{m_{i}L_{i}C_{i}\dot{\beta}_{i}}{2} - C_{i} \rho_{A_i}\sum_{j = 1}^{r} \int _{0}^{L_{i}} Y_{ij}\dot{q}_{ij}\,dt - S_{i}\dot{\beta}_{i}\rho_{A_i}\sum _{j = 1}^{r} \int_{0}^{L_{i}} Y_{ij}q_{ij}\,dt,\quad (i = 1,2,3) \\ \end{aligned}$$

(81)

$$\begin{aligned} C_{22} =& \left[ \begin{array}{@{}c@{\quad}c@{}} \int_{0}^{L_{1}} \rho_{A_1}(\sum_{j = 1}^{r} Y_{1j}q_{1j})(\sum_{j = 1}^{r} Y_{1j}\dot{q}_{1j})\,dt & 0 \\ 0 & \int_{0}^{L_{2}} \rho_{A_2}(\sum_{j = 1}^{r} Y_{2j}q_{2j})(\sum_{j = 1}^{r} Y_{2j}\dot{q}_{2j})\,dt \\ 0 & 0 \end{array}\right. \\ &\phantom{[}\quad{} \left.\begin{array}{@{}c@{}} 0\\ 0\\ \int_{0}^{L_{3}} \rho_{A_3}(\sum_{j = 1}^{r} Y_{3j}q_{3j})(\sum _{j = 1}^{r} Y_{3j}\dot{q}_{3j})\,dt \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(82)

$$\begin{aligned} C_{14} =& - \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \dot{\beta}_{1}C_{1}\int_{0}^{L_{1}} \rho_{A_1}Y_{11}\,dx & \ldots& \dot{\beta}_{1}C_{1}\int_{0}^{L_{1}} \rho_{A_1}Y_{1r}\,dx & 0 & \ldots \\ 0 & \ldots& 0 & \dot{\beta}_{2}C_{2}\int_{0}^{L_{2}} \rho_{A_2}Y_{21}\,dx & \ldots\\ 0 & \ldots& 0 & 0 & \ldots\\ \end{array}\right. \\ &\phantom{-[}\quad{} \left.\begin{array}{@{}c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{}} 0 & 0 & \ldots& 0 \\ \dot{\beta}_{2}C_{2}\int_{0}^{L_{2}} \rho_{A_2}Y_{2r}\,dx & 0 & \ldots& 0 \\ 0 & \dot{\beta}_{3}C_{3}\int_{0}^{L_{3}} \rho_{A_3}Y_{31}\,dx & \ldots& \dot{\beta}_{3}C_{3}\int_{0}^{L_{3}} \rho_{A_3}Y_{3r}\,dx \end{array} \right] \in R^{3 \times3r} \\ \end{aligned}$$

(83)

$$\begin{aligned} C_{24} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} C_{24}^{1} & 0 & 0 \\ 0 & C_{24}^{2} & 0 \\ 0 & 0 & C_{24}^{3} \end{array} \right] \in R^{3 \times3r} \end{aligned}$$

(84)

$$\begin{aligned} C_{24}^{i} =& \Biggl[\dot{\beta}_{i} \int_{0}^{L_{i}} \rho_{A_i}Y_{i1}\sum _{j = 1}^{r} Y_{ij}q_{ij} \,dx\quad \ldots\quad \dot{\beta}_{i}\int_{0}^{L_{i}} \rho_{A_i}Y_{1r}\sum_{j = 1}^{r} Y_{ij}q_{ij}\,dx \Biggr] \in R^{1 \times r} \end{aligned}$$

(85)

$$\begin{aligned} K =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & K_{f} \end{array} \right] \in R^{(9 + 3r) \times(9 + 3r)} \end{aligned}$$

(86)

$$\begin{aligned} K_{f} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} K_{f}^{1} & 0 & 0 \\ 0 & K_{f}^{2} & 0 \\ 0 & 0 & K_{f}^{3} \end{array} \right] \in R^{3r \times3r} \end{aligned}$$

(87)

$$\begin{aligned} K_{f}^{i} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} EI\int_{0}^{L_{i}} Y_{i1}^{\prime\prime 2}\,dx & \ldots& 0 \\ \vdots& \ldots& \vdots\\ 0 & \ldots& EI\int_{0}^{L_{i}} Y_{ir}^{\prime\prime 2}\,dx \end{array} \right] \in R^{r \times r} \end{aligned}$$

(88)

$$\begin{aligned} J_{\varGamma} =& [J_{f\rho}\quad J_{f\beta}\quad J_{fp} \quad J_{fw}]^{T} \in R^{(3r + 9) \times6} \end{aligned}$$

(89)

$$\begin{aligned} J_{f\rho} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1x} & a_{1y} & 0 & 0 & 0 & 0 \\ 0 & 0 & a_{2x} & a_{2y} & 0 & 0 \\ 0 & 0 & 0 & 0 & a_{3x} & a_{3y} \end{array} \right] \in R^{3 \times6} \end{aligned}$$

(90)

where $\bar{a}_{i} = (a_{ix},a_{iy}) = (\cos\alpha_{i},\sin\alpha_{i})$

$$ J_{f\beta} = \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} - b_{1y} & b_{1x} & 0 & 0 & 0 & 0 \\ 0 & 0 & - b_{2y} & b_{2x} & 0 & 0 \\ 0 & 0 & 0 & 0 & - b_{3y} & b_{3x} \end{array} \right] \in R^{3 \times6} $$

(91)

where $\bar{b}_{i}\,{=}\,(b_{ix},b_{iy})\,{=}\,(L_{i}\cos\beta_{i} - \sin \beta_{i}\sum_{j = 1}^{r} Y_{ij}(L_{i})q_{ij},L_{i}\sin\beta_{i} + \cos \beta_{i}\sum_{j = 1}^{r} Y_{ij}(L_{i})q_{ij} )$

$$\begin{aligned} J_{fw} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} J_{fw}^{1} & 0 & 0 \\ 0 & J_{fw}^{2} & 0 \\ 0 & 0 & J_{fw}^{3} \end{array} \right] \in R^{3r \times6} \end{aligned}$$

(92)

$$\begin{aligned} J_{fw}^{i} =& \left[ \begin{array}{@{}c@{\quad}c@{}} - \sin\beta_{i} & \cos\beta_{i} \\ \vdots& \vdots\\ - \sin\beta_{i} & \cos\beta_{i} \end{array} \right] \in R^{r \times2} \end{aligned}$$

(93)

$$\begin{aligned} J_{p} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} \frac{b_{1x}}{\bar{a}_{1} \cdot \bar{b}_{1}} & \frac{b_{1y}}{\bar{a}_{1} \cdot\bar{b}_{1}} & \frac{e_{1x}b_{1y} - e_{1y}b_{1x}}{\bar{a}_{1} \cdot\bar{b}_{1}} \\ \frac{b_{2x}}{\bar{a}_{2} \cdot\bar{b}_{2}} & \frac{b_{2y}}{\bar{a}_{2} \cdot\bar{b}_{2}} & \frac{e_{2x}b_{2y} - e_{2y}b_{2x}}{\bar{a}_{2} \cdot \bar{b}_{2}} \\ \frac{b_{3x}}{\bar{a}_{3} \cdot\bar{b}_{3}} & \frac{b_{3y}}{\bar{a}_{3} \cdot\bar{b}_{3}} & \frac{e_{3x}b_{3y} - e_{3y}b_{3x}}{\bar{a}_{3} \cdot \bar{b}_{3}} \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(94)

$$\begin{aligned} J_{\beta} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} \frac{ - a_{1y}}{\bar{a}_{1} \cdot \bar{b}_{1}} & \frac{a_{1x}}{\bar{a}_{1} \cdot\bar{b}_{1}} & \frac{\bar{a}_{1} \cdot\bar{e}_{1}}{\bar{a}_{1} \cdot\bar{b}_{1}} \\ \frac{ - a_{2y}}{\bar{a}_{2} \cdot\bar{b}_{2}} & \frac{a_{2x}}{\bar{a}_{2} \cdot\bar{b}_{2}} & \frac{\bar{a}_{2} \cdot\bar{e}_{2}}{\bar{a}_{2} \cdot \bar{b}_{2}} \\ \frac{ - a_{3y}}{\bar{a}_{3} \cdot\bar{b}_{3}} & \frac{a_{3x}}{\bar{a}_{3} \cdot\bar{b}_{3}} & \frac{\bar{a}_{3} \cdot\bar{e}_{3}}{\bar{a}_{3} \cdot \bar{b}_{3}} \end{array} \right] \in R^{3 \times3} \end{aligned}$$

(95)

$$\begin{aligned} J_{pw} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} Y_{11}\sum_{j = 1}^{r} Y_{1j}(L_{1})q_{1j} & \ldots& Y_{1r}\sum_{j = 1}^{r} Y_{1j}(L_{1})q_{1j} & 0 & 0\\ 0 & 0 & 0 & Y_{21}\sum_{j = 1}^{r} Y_{2j}(L_{2})q_{2j} & \ldots\\ 0 & 0 & 0 & 0 & 0 \end{array}\right. \\ &\quad{}\left.\begin{array}{@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 0 \\ Y_{2r}\sum_{j = 1}^{r} Y_{2j}(L_{2})q_{j} & 0 & 0 & 0 \\ 0 & Y_{31}\sum_{j = 1}^{r} Y_{3j}(L_{3})q_{3j} & \ldots & Y_{3r}\sum_{j = 1}^{r} Y_{3j}(L_{3})q_{3j} \end{array} \right] \in R^{3 \times3r} \\ \end{aligned}$$

(96)

$$\begin{aligned} J_{\beta w} =& \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \frac{\cos(\alpha_{1} + \beta_{1})Y_{11}(L_{1})}{\bar{a}_{1} \cdot\bar{b}_{1}} & \ldots& \frac{\cos(\alpha_{1} + \beta_{1})Y_{1r}(L_{1})}{\bar{a}_{1} \cdot \bar{b}_{1}} & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{\cos(\alpha_{2} + \beta_{2})Y_{21}(L_{2})}{\bar{a}_{2} \cdot\bar{b}_{2}} & \ldots& \frac{\cos(\alpha_{2} + \beta_{2})Y_{2r}(L_{2})}{\bar{a}_{2} \cdot\bar{b}_{2}} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right. \\ &\quad{} \left.\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{\cos(\alpha_{3} + \beta_{3})Y_{31}(L_{3})}{\bar{a}_{3} \cdot\bar{b}_{3}} & \ldots& \frac{\cos(\alpha_{3} + \beta_{3})Y_{3r}(L_{3})}{\bar{a}_{3} \cdot \bar{b}_{3}} \end{array} \right] \in R^{3 \times3r} \end{aligned}$$

(97)