Skip to main content
SpringerLink
Log in

Efficient methodology for multibody simulations with discontinuous changes in system definition

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

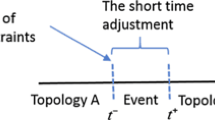
A new method is presented for accurately and efficiently simulating multi-scale multibody systems with discontinuous changes in system definitions as encountered in adaptive switching between models with different resolutions as well as models with different system topologies. An example of model resolution change is a transition of a system from a discrete particle model to a reduced order articulated multi-rigid body model. The discontinuous changes in system definition may be viewed as an instantaneous change (release or impulsive application of) the system constraints. The method uses a spatial impulse–momentum formulation in a divide and conquer scheme. The approach utilizes a hierarchic assembly–disassembly process by traversing the system topology in a binary tree map to solve for the jumps in the system generalized speeds and the constraint impulsive loads in linear and logarithmic cost in serial and parallel implementations, respectively. The method is applicable for systems in serial chain as well as kinematical loop topologies. The coupling between the unilateral and bilateral constraints is handled efficiently through the use of kinematic joint definitions. The equations of motion for the system are produced in a hierarchic sub-structured form. This has the advantage that changes in sub-structure definitions/models results in a change to the system equations only within the associated sub-structure. This allows for significant changes in model types and definitions without having to reformulate the equations for the whole system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Piedboeuf, J., Gonthier, Y., McPhee, J., Lange, C.: A regularized contact model with asymmetric damping and dwell-time dependent friction. Multibody Syst. Dyn. 11, 209–233 (2004)

    Article  MATH  Google Scholar 

  2. Bei, Y., Fregly, B.J.: Multibody dynamic simulation of knee contact mechanics. Med. Eng. Phys. 26(9), 777–789 (2004)

    Article  Google Scholar 

  3. Glocker, C., Pfeiffer, P.: Multiple impacts with friction in multibody systems. Nonlinear Dyn. 7, 471–497 (1995)

    Article  MathSciNet  Google Scholar 

  4. Pfeiffer, F.G.: Applications of unilateral multibody dynamics. Philos. Trans. Roy. Soc. Lond. 359(1789), 2609–2628 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  5. Pfieffer, F., Glocker, C.: Multibody Dyanmics with Unilateral Constraints. CISM Courses and Lectures, vol. 421, International Centre for Mechanical Sciences. Springer, New York (2000)

    Google Scholar 

  6. Stewart, D.E.: Rigid-body dynamics with friction and impact. SIAM Rev. 42(1), 3–39 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  7. Ambrósio, J.A.C., Pereira, M.S., Dias, J.P.: Crashworthiness analysis and design using rigid-flexible multibody dynamics with applications to train vehicles. Int. J. Num. Method. Eng. 40(4), 655–687 (1997)

    Article  MATH  Google Scholar 

  8. Ambrósio, J.A.C., Pereira, M.S., Dias, J.P.: Contact and impact models for vehicle crashworthiness simulation. Int. J. Crashworth. 8, 73–86 (2003)

    Article  Google Scholar 

  9. Barhorst, D.: Issues in computing contact forces for non-penetrating rigid bodyes. Algoritmica 10, 292–352 (1993)

    Article  Google Scholar 

  10. Keller, J.B.: Impact with friction. J. Appl. Mech. 53(1), 1–4 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  11. Lötstedt, P.: Mechanical systems of rigid bodies subject to unilateral constraints. SIAM J. Appl. Math. 42(2), 281–296 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  12. Trinkle, J., Zeng, D., Sudarsky, S., Lo, G.: On dynamic multi-rigid-body contact problems with Coulomb friction. Z. Angew. Math. Mech. 77(4), 267–279 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  13. Wu, S., Haug, E.J., Yang, S.M.: Dynamics of mechanical systems with Coulomb friction, stiction, impact and constraint addition–deletion. Mech. Mach. Theory 21(5), 401–425 (1986)

    Article  Google Scholar 

  14. Ferris, M.C., Mangasarian, O.L., Pang, J.S.: Complementarity: applications, algorithms and extensions. In: Applied Optimization, vol. 50. Kluwer Academic, Dordrecht (2001)

    Google Scholar 

  15. Brenan, K.E., Campbell, S.L., Petzold, L.R.: Numerical Solutions of Initial-value Problems in Differential-Algebraic Equations. North-Holland, New York (1989)

    Google Scholar 

  16. Anderson, K.S.: An order-n formulation for the motion simulation of general multi-rigid-body tree systems. Comput. Struct. 46(3), 547–559 (1993)

    Article  MATH  Google Scholar 

  17. Rosenthal, D.E.: An order n formulation for robotic systems. J. Astronaut. Sci. 38(4), 511–529 (1990)

    Google Scholar 

  18. Jain, A.: Unified formulation of dynamics for serial rigid multibody systems. J. Guid. Control Dyn. 14(3), 531–542 (1991)

    Article  MATH  Google Scholar 

  19. Featherstone, R.: The calculation of robotic dynamics using articulated body inertias. Int. J. Robot. Res. 2(1), 13–30 (1983)

    Article  Google Scholar 

  20. Anderson, K.S., Sadowski, M.J.: An efficient method for contact/impact problems in multibody systems: tree topologies. In: Proceedings of the Fourth International Symposium on Multibody Dynamics and Vibrations, ASME Design Engineering Technical Conference 2003, (DETC03), number DETC03/VIB-48338, Chicago, IL, 2–6 September 2003

  21. Seabra Pereira, M., Nikravesh, P.: Impact dynamics of multibody systems with frictional contact using joint coordinates and canonical equations of motion. Nonlinear Dyn. 9, 53–71 (1996)

    Article  MathSciNet  Google Scholar 

  22. Featherstone, R.: A divide-and-conquer articulated body algorithm for parallel O(log (n)) calculation of rigid body dynamics. Part 1: Basic algorithm. Int. J. Robot. Res. 18(9), 867–875 (1999)

    Article  Google Scholar 

  23. Mukherjee, R., Anderson, K.S.: An orthogonal complement based divide-and-conquer algorithm for constrained multibody systems. Nonlinear Dyn. 48(1–2), 199–215 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Featherstone, R.: Robot Dynamics Algorithms. Kluwer Academic, New York (1987)

    Google Scholar 

  25. Mukherjee, R., Anderson, K.S.: A logarithmic complexity divide-and-conquer algorithm for multi-flexible articulated body dynamics. J. Comput. Nonlinear Dyn. 2(1), 10–21 (2007)

    Article  MathSciNet  Google Scholar 

  26. Kim, S.S., VanderPloeg, M.J.: Generalized and efficient method for dynamic analysis of mechanical systems using velocity transforms. J. Mech. Transm. Autom. Des. 108(2), 176–182 (1986)

    Article  Google Scholar 

  27. Nikravesh, P.E.: Systematic reduction of multibody equations to a minimal set. Int. J. Nonlinear Mech. 25(2–3), 143–151 (1990)

    Article  MATH  Google Scholar 

  28. Forrest, L.R., Crozier, P.S., Stevens, M.J., Woolf, T.B.: Molecular dynamics simulation of dark-adapted rhodopsin in an explicit membrane bilayer: coupling between local retinal and larger scale conformational changes. J. Mol. Biol. 333, 493–514 (2003)

    Article  Google Scholar 

  29. Kane, T.R., Levinson, D.A.: Dynamics: Theory and Application. Mcgraw-Hill, New York (1985)

    Google Scholar 

  30. Flaherty, J.E., Loy, R.M., Ozturan, C., Shephard, M.S., Szymanski, B.K., Teresco, J.D., Ziantz, L.H.: Parallel structures and dynamic load balancing for adaptive finite element computations. Appl. Numer. Math. 26(1–2), 241–263 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  31. Featherstone, R.: A divide-and-conquer articulated body algorithm for parallel O(log (n)) calculation of rigid body dynamics. Part 2: Trees, loops, and accuracy. Int. J. Robot. Res. 18(9), 876–892 (1999)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical, Aeronautical, and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY, 12180, USA

    Rudranarayan M. Mukherjee & Kurt S. Anderson

Authors
  1. Rudranarayan M. Mukherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kurt S. Anderson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rudranarayan M. Mukherjee.

Additional information

R.M. Mukherjee is now at Jet Propulsion Laboratory, Pasadena, California

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mukherjee, R.M., Anderson, K.S. Efficient methodology for multibody simulations with discontinuous changes in system definition. Multibody Syst Dyn 18, 145–168 (2007). https://doi.org/10.1007/s11044-007-9075-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-007-9075-1

Keywords

Search

Navigation