1 Introduction

In engineering, many problems describing mechanical vibrations in elastic structures, such as for instance the vibrations of power transmission lines [13] and bridge cables [16], can be mathematically represented by initial-boundary-value problems for a wave or a beam equation. Understanding the transverse vibrations of beams is important to prevent serious failures of the structures. In order to suppress the undesired vibrations of the mechanical structures different kinds of dampers such as tuned mass dampers and oil dampers can be used at the boundary. Analysis of the transversally vibrating beam problems with boundary damping is still of great interest today, and has been examined for a long time by many researchers [12, 23, 25]. In order to obtain a general insight into the over-all behavior of a solution, having a closed form expression which represents a solution, can be very convenient. The Green’s function technique is one of the few approaches to obtain integral representations for the solution [10].

In many papers and books, the vibrations of elastic beams have been studied by using the Green’s function technique. A good overview can be found in e.g. [8, 9] and [7, 10, 24] for initial-value problems and for initial-boundary value problems, respectively. The initial-boundary value problem for a semi-infinite clamped bar has already been solved to obtain its Green’s function by using the method of Laplace tranforms [21]. To our best knowledge, we have not found any literature on the explicit construction of a Green’s function for semi-infinite beam with boundary damping.

The outline of the present paper is as follows. In Sect. 2, we establish the governing equations of motion. The aim of the paper is to give explicit formula for the Green’s function for the following semi-infinite pinned, slided, clamped and damped vibrating beams as listed in Table 1. In Sect. 3, we use the method of Laplace transforms to construct the (exact) solution and also derive closed form expressions for the Green’s functions for these problems. In Sect. 4, three classical boundary conditions are considered and the Green’s functions for semi-infinite beams are represented by definite integrals. For pinned and sliding vibrating beams, it is shown how the exact solution can be written with respect to even and odd extensions of the Green’s function. In Sect. 5, we consider transversally vibrating elastic beams with non-classical boundary conditions such as dampers. The analytical results for semi-infinite beams in this case are compared with numerical results on a bounded domain [0, L] with L large. The damping properties are given by the roots of denominator part in the Laplace approach, or equivalently by the characteristic equation. Numerical and asymptotic approximations of the roots of a characteristic equation for the beam-like problem on a finite domain will be calculated. It will be shown how boundary damping can be effectively used to suppress the amplitudes of oscillation. In Sect. 6, the concept of local energy storage is described. Finally some conclusions will be drawn in Sect. 7.

Table 1 Boundary conditions (BCs) for beams which are infinitely long in one direction
Full size table

2 Governing equations of motion

We will consider the transverse vibrations of a one-dimensional elastic Euler–Bernoulli beam which is infinitely long in one direction. The equations of motion can be derived by using Hamilton’s principle [17]. The function u(x, t) is the vertical deflection of the beam, where x is the position along the beam, and t is the time. Let us assume that gravity can be neglected. The equation describing the vertical displacement of the beam is given by

$$\ddot{u}+a^{2}\,u^{\prime \prime \prime \prime }={q \over \rho A} ,\quad 0<x<\infty ,\quad t>0,$$
(1)
$$u(x,0)=f(x),\quad \dot{u}(x,0)=g(x),\quad 0 \le x<\infty ,$$
(2)

where \(a^{2}=(EI/ \rho A)>0\). E is Young’s modulus of elasticity, I is the moment of inertia of the cross-section, \(\rho\) is the density, A is the area of the cross-section, and q is an external load. Here, f(x) represents the initial deflection and g(x) the initial velocity. Note that the overdot \(( \cdot )\) denotes the derivative with respect to time and the prime \(()^{\prime }\) denotes the derivative with respect to the spatial variable x.

In the book of Guenther and Lee [9], and Graff [8], the solution of the Euler–Bernoulli beam Eq. (1) with q = 0 on an infinite domain is obtained by using Fourier transforms, and is given by

$$u(x,t)=\int _{-\infty }^{\infty }\left[ K(\xi -x,t)f(\xi )+L(\xi -x,t)g(\xi )\right] \,\text {d} \xi ,$$
(3)

where

$$K(x,t)=\frac{1}{\sqrt{4\pi a\,t}}\sin \left( \frac{x^2}{4at}+{\pi \over 4}\right) ,$$
(4)

and

$$L(x,t)=\frac{x}{2a}\left[ S \left( \frac{x^2}{4at}\right) -C \left( \frac{x^2}{4at} \right) \right] +2\,tK(x,t).$$
(5)

Here the functions C(z) and S(z) are the Fresnel integrals defined by

$$C(z)= \int _{0}^{z}{\cos (s) \over {\sqrt{s}}}\text {d}s ,\quad \text {and }\;S(z)= \int _{0}^{z} {\sin (s) \over {\sqrt{s}}} \text {d}s .$$
(6)

In order to put the Eqs. (1) and (2) in a non-dimensional form the following dimensionless quantities are used:

$$\begin{aligned}&u(x,t)=\frac{u^*(x^*,t^*)}{L_{*}},\, x=\frac{x^*}{L_{*}},\, t=\frac{\kappa t^*}{L_{*}},\, \kappa =\frac{1}{L_{*}} {\sqrt{\frac{EI}{\rho A}}},\\&f(x)=\frac{f^*(x^*)}{L_{*}},g(x)=\,\frac{g^*(x^*)}{\kappa },q(x,t)=\frac{q^*(x^*,t^*) \rho A \kappa ^{2}}{L_{*}}, \end{aligned}$$

where \(L_{*}\) is the dimensional characteristic quantity for the length , and by inserting these non-dimensional quantities into Eqs. (1) and (2), we obtain the following initial-boundary value problem:

$$\ddot{u}(x,t)+u^{\prime \prime \prime \prime }(x,t)=q(x,t) ,\quad 0<x<\infty ,\quad t>0,$$
(7)
$$u(x,0)=f(x),\quad \dot{u}(x,0)=g(x),\quad 0 \le x<\infty ,$$
(8)

and the boundary conditions at x = 0 are given in Table 1. The asterisks indicating the dimensional quantities are omitted in Eqs. (7) and (8), and henceforth for convenience.

In the coming sections, we will show how the Green’s functions for semi-infinite beams with boundary conditions given at x = 0, can be obtained in explicit form.

3 The Laplace transform method

In this section, Green’s functions will be constructed by using the Laplace transform method in order to obtain an exact solution for the initial-boundary value problem Eqs. (7) and (8). Let us assume that the external force \(q(x,t)=\delta (x-\xi ) \otimes \delta (t)\) at the point \(x=\xi\) at time t = 0, \(\delta\) being Dirac’s function, and \(f(x)=g(x)=0\). The Green’s function \(G_{\xi }(x,t)\), \(\xi >0\), expresses the displacements along the semi-infinite beam.

We start by defining the Laplace operator as an integration with respect to the time variable t. The Laplace transform \(g_{\xi }\) of \(G_{\xi }\) with respect to t is defined as

$$g_{\xi }(x,p)={\mathcal {L}}\{G_{\xi } (x,t)\}=\int _{0}^{\infty } \text {e}^{-pt} G_{\xi } (x,t) \text {d}t,$$
(9)

where \(g_{\xi }\) is the Green’s function of the differential operator \(L=(\text {d}^{4}/\text {d}x^{4})+p^{2}\) on the interval \((0,\infty )\). The Green’s function \(g_{\xi }\) satisfies the following properties [14]:

  • [G1] The Green’s function \(g_{\xi }\) satisfies the fourth order ordinary differential equation in each of the two subintervals \(0< x< \xi\) and \(\xi<x< \infty\), that is, \(Lg_{\xi }=0\) except when \(x=\xi\).

  • [G2] The Green’s function \(g_{\xi }\) satisfies at x = 0 one of the homogeneous boundary conditions, as given in Table 1.

  • [G3] The Green’s function \(g_{\xi }\) and its first and second order derivatives exist and are continuous at \(x=\xi\).

  • [G4] The third order derivative of the Green’s function \(g_{\xi }\) with respect to x has a jump discontinuity which is defined as

    $$\lim _{\epsilon \rightarrow \ 0} \left[ g^{\prime \prime \prime }_{\xi }(\xi +\epsilon )-g^{\prime \prime \prime }_{\xi }(\xi -\epsilon )\right] =1.$$
    (10)

The transverse displacement u(x, t) of the beam can be represented in terms of the Green’s function as (see also [22]):

$$\begin{aligned} u(x,t)= & {} \int _{0}^{\infty } f(\xi ) \,\dot{G}_{\xi }(x,t)\,\text {d} \xi +\int _{0}^{\infty } g(\xi ) \,G_{\xi }(x,t)\, \text {d} \xi \\&\quad +\,\int _{0}^{t} \int _{0}^{\infty } q(\xi ,\tau )\,G_{\xi }(x,t-\tau ) \text {d} \xi \,\text {d} \tau . \end{aligned}$$
(11)

In the coming sections, we solve exactly the initial-boundary value problem for a beam on a semi-infinite interval for different types of boundary conditions.

4 Classical boundary conditions

4.1 Pinned end, \(u=u_{xx}=0\)

In this section, we consider a semi-infinite beam equation, when the displacement and the bending moment are specified at x = 0, i.e. \(u(0,t)=u_{xx}(0,t)=0\), and when the beam has an infinite extension in the positive x-direction.

By using the requirements [G1]–[G4], \(g_{\xi }\) is uniquely determined, and we obtain

$$\begin{aligned} g_{\xi }= & {} \frac{1}{8 \beta ^{3}} \left\{ \text {e}^{-\beta |x- \xi |} \left[ \text {cos} \beta (x- \xi ) + \text {sin} \beta |x- \xi |\right] \right. \\&\left. \quad +\, \text {e}^{-\beta (x+ \xi )} \left[ -\text {cos} \beta (x+ \xi ) - \text {sin} \beta (x+ \xi )\right] \right\} , \end{aligned}$$
(12)

where \(\beta ^{2}=p/2\). In order to invert the Laplace transform, we use the formula (see [3], page 93)

$${\mathcal {L}} ^{-1} \left[ \left( \sqrt{p^2}\right) ^{-1} \phi \left( \sqrt{p^2}\right) \right] =\int _{0}^{t} {\mathcal {L}} ^{-1} \{ \phi (\tau ) \} \,\text {d} \tau ,$$
(13)

and (see [19], page 279)

$${\mathcal {L}} ^{-1} \left[ p^{-1/2} \text {e}^{-\sqrt{pz}} \text {cos}(\sqrt{pz}) \right] ={ \frac{1}{\sqrt{\pi t}} \text {cos} \left( \frac{z}{2t}\right) },$$
(14)
$${\mathcal {L}} ^{-1} \left[ p^{-1/2} \text {e}^{-\sqrt{pz}} \text {sin}(\sqrt{pz}) \right] ={ \frac{1}{\sqrt{\pi t}} \text {sin} \left( \frac{z}{2t}\right) },$$
(15)

where \(z=\frac{|x\pm \xi |}{\sqrt{2}}\). The Green’s function yields

$$G_{\xi } (x,t)= - \int _{0}^{t} \left[ K(\xi -x,\tau )-K(\xi +x,\tau ) \right] \text {d} \tau ,$$
(16)

where the kernel function is defined by

$$K(x,\tau )={\frac{1}{\sqrt{4 \pi \tau }}} \, \text {sin} \left( {\frac{x^2}{4 \tau }}+{\frac{\pi }{4}} \right) .$$
(17)

When we assume for Eqs. (7) and (8) that the external loading is absent (q = 0), and that the initial displacement f(x) and the initial velocity g(x) are nonzero, one can find the solution of the pinned end semi-infinite beam in the form of Eq. (3) as

$$\begin{aligned} u(x,t)= & {} \int _{0}^{\infty } \left[ [ K(\xi -x,t)-K(\xi +x,t)]f(\xi )\right. \\&\left. \quad +\,[ L(\xi -x,t)-L(\xi +x,t)]g(\xi ) \right] \,\text {d} \xi , \end{aligned}$$
(18)

where K and L are given by Eqs. (4) and (5).

It should be observed that Eq. (18) could have been obtained by using Eq. (3) and the boundary conditions \(u=u_{xx}=0\) at x = 0. From which it simply follows that f and g should be extended as odd functions in their argument, and then by simplifying the so-obtained integral, one obtains Eq. (18).

On the other hand, when we consider that the external loading is nonzero, for example, \(q=\delta (x-\xi ) \otimes \delta (t)\), and the initial disturbances are zero (\(f=g=0\)), the solution of pinned end semi-infinite beam can be written in a non-dimensional form. By substituting the following dimensionless quantities in Eq. (16)

$$v=\frac{x}{\xi },\; s=\frac{t}{\xi ^{2}},\; \sigma =\frac{t}{\tau },\; g(v,s)=\frac{G_{\xi }}{\xi }.$$
(19)

We obtain

$$\begin{aligned} g(v,s)= & {} -\sqrt{\frac{s}{4\pi }} \int _{1}^{\infty } \left[ \text {sin} \left( {\frac{\sigma (v-1)^2}{4s}}+{\frac{\pi }{4}} \right) \right. \\&\left. -\,\text {sin} \left( {\frac{\sigma (v+1)^2}{4s}}+{\frac{\pi }{4}} \right) \right] \frac{\text {d} \sigma }{\sigma ^{3/2}}. \end{aligned}$$
(20)

Figure 1 shows the shape of the semi-infinite one-sided pinned beam during its oscillation. It can be observed how the amplitude of the impulse at \(x=\xi\) is increasing and how the deflection curves start to develop rapidly from the boundary at x = 0 as new time variable s is increasing, where s is given by Eq. (19).

Fig. 1
figure 1

The Green’s function g(v, s) for a pinned end semi-infinite beam with the initial values \(g(v,0)=0,\,g_{s}(v,0)=0\), and the external force \(q(v,s)=\delta (v-1) \otimes \delta (s)\)

Full size image

4.2 Sliding end, \(u_{x}=u_{xxx}=0\)

In this section, we consider a semi-infinite beam equation for \(x>0\), when the bending slope and the shear force are specified at x = 0, i.e. \(u_{x}(0,t)=u_{xxx}(0,t)=0\). The same method which is used in Sect. 4.1 to obtain the Green’s function can also be applied for the sliding end semi-infinite beam. The Green’s function is given by

$$G_{\xi } (x,t)= \int _{0}^{t} \left[ K(\xi -x,\tau )+K(\xi +x,\tau ) \right] \text {d} \tau ,$$
(21)

and the transverse displacement u(x, t) of the beam without an external loading is given by

$$\begin{aligned} u(x,t)=&\int _{0}^{\infty } \left[ [ K(\xi -x,t)+K(\xi +x,t)]f(\xi )\right. \\&\left. +\,[ L(\xi -x,t)+L(\xi +x,t)]g(\xi ) \right] \,\text {d} \xi . \end{aligned}$$
(22)

Equation (22) also could have been obtained by using Eq. (3) and the boundary conditions \(u_{x}=u_{xxx}=0\) at x = 0. It follows that f and g should be extended as even functions in their argument, and then by simplifying the so-obtained integral, we obtain Eq. (22).

By using the same dimensionless quantities as in Sect. 4.1, the non-dimensional form of the solution for the sliding end semi-infinite beam is given by:

$$\begin{aligned} g(v,s)= & {} -\sqrt{\frac{s}{4\pi }} \int _{1}^{\infty } \left[ \text {sin} \left( {\frac{\sigma (v-1)^2}{4s}}+{\frac{\pi }{4}} \right) \right. \\&\left. \quad +\,\text {sin} \left( {\frac{\sigma (v+1)^2}{4s}}+{\frac{\pi }{4}} \right) \right] \frac{\text {d} \sigma }{\sigma ^{3/2}}. \end{aligned}$$
(23)

Similarly, Fig. 2 demonstrates the shape of the semi-infinite one-sided sliding beam during its oscillation. It can be seen how the amplitude of the impulse at \(x=\xi\) is increasing and how the deflection curve is developing from the boundary at x = 0 as the new time variable s is increasing.

Fig. 2
figure 2

The Green’s function g(v, s) for a sliding end semi-infinite beam with the initial values \(g(v,0)=0,\,g_{s}(v,0)=0\), and the external force \(q(v,s)=\delta (v-1) \otimes \delta (s)\)

Full size image

4.3 Clamped end, \(u=u_{x}=0\)

In this section, we consider a semi-infinite beam equation for \(x>0\), when the deflection and the slope are specified at x = 0, i.e. \(u(0,t)=u_{x}(0,t)=0\). The non-dimensional form for the Green’s function of the semi-infinite vibrating beam is now given by

$$\begin{aligned} g(v,s)=&-\sqrt{\frac{s}{4\pi }} \int _{1}^{\infty } \left[ \text {sin} \left( {\frac{\sigma (v-1)^2}{4s}}+{\frac{\pi }{4}} \right) \right. \\&-\,\text {sin} \left( {\frac{\sigma (v+1)^2}{4s}}+{\frac{\pi }{4}} \right) \\&\left. -\,\sqrt{2} \text {e}^{ -\sigma v/2s} \text {cos} \left( {\frac{\sigma (v^2-1)}{4s}} \right) \right] \frac{\text {d} \sigma }{\sigma ^{3/2}}. \end{aligned}$$
(24)

Figure 3 depicts the fading-out waves for the elastic beam which is clamped at the boundary. For the simple cases (i.e., for the pinned, sliding and clamped cases), we compared our results with some of the available, analytical results in the literature [20, 21]. Our results agreed completely with those results.

Fig. 3
figure 3

The Green’s function g(v, s) for a fixed (clamped) end semi-infinite beam with the initial values \(g(v,0)=0,\,g_{s}(v,0)=0\), and the external force \(q(v,s)=\delta (v-1) \otimes \delta (s)\)

Full size image

5 Non-classical boundary condition

5.1 Damper end, \(u_{xx} = 0\), \(u_{xxx}=-\tilde{\lambda } {u}_{t}\)

In this section, we consider a semi-infinite beam equation for \(x>0\), when the bending moment is zero and the shear force is proportional to the velocity (damper) at x = 0, i.e. \(EIu_{xx} =0,\;EIu_{xxx}=-\alpha {u}_{t}\). After applying the dimensionless quantities \(\tilde{\lambda }={\alpha L_{*}/ \sqrt{EI\rho A}}\) to the damper boundary conditions, it follows that \(u_{xx}=0\, ,u_{xxx}=-\tilde{\lambda } u_{t}\). We obtain the Green’s function for the semi-infinite beam in a similar way as shown in the previous cases. By using the requirements [G1]–[G4], \(g_{\xi }\) is uniquely determined, and we obtain

$$\begin{aligned} g_{\xi }=&\,\frac{1}{8 \beta ^{3}} \left\{ \text {e}^{-\beta |x- \xi |} [\text {cos} \beta (x- \xi ) + \text {sin} \beta |x- \xi |]\right. \\&+\, \text {e}^{-\beta (x+ \xi )} [-\text {cos} \beta (x+ \xi ) - \text {sin} \beta (x+ \xi )] \\&\left. + \frac{4\beta ^{3} \text {e}^{-\beta (x+ \xi )} }{2 \beta ^{3} + \tilde{\lambda } p}[\text {cos} \beta (x- \xi ) + \text {cos} \beta (x+ \xi )]\right\} , \end{aligned}$$
(25)

where \(\beta ^{2}=p/2\). In order to invert the Laplace transform, we use the formula (see [3], page 93)

$${\mathcal {L}} ^{-1} \left[ p^{-1} \phi (p) \right] =\int _{0}^{t} {\mathcal {L}} ^{-1} \{ \phi (\tau ) \} \,\text {d} \tau .$$
(26)

Here

$$\begin{aligned} \phi (p)& = \frac{p^{-1/2}}{2\sqrt{2}} {\text{e}}^{-\sqrt{p \eta }} [ {\text {cos}}(\sqrt{p\eta })+ {\text {sin}}(\sqrt{p\eta })] \\&-\,\frac{p^{-1/2}}{2\sqrt{2}} {\text {e}}^{-\sqrt{p \mu }} [ {\text{cos}}(\sqrt{p\mu })+ {\text {sin}}(\sqrt{p\mu })] \\&+ \,\frac{p^{-1/2}}{2\sqrt{2}}{\text {e}}^{-\sqrt{p \mu }} \frac{2 p^{3/2}}{p^{3/2}+\sqrt{2} {\tilde{\lambda }} p} [ {\text {cos}}(\sqrt{p\eta })+ {\text {cos}}(\sqrt{p\mu })], \end{aligned}$$
(27)

where \(\eta =\frac{(x+\xi )}{\sqrt{2}}\) and \(\mu =\frac{|x-\xi |}{\sqrt{2}}\). In Eq. (27), we use Eqs. (14) and (15) for the first two terms, and the following convolution theorem for the last term (see [3], page 92)

$${\mathcal {L}} ^{-1} \left[ \phi _{1} (p) \,\phi _{2} (p)\right] =f_{1}(t)*f_{2}(t) =\int _{0}^{t}{f_{1}(r)f_{2}(t-r)\text {d}r},$$
(28)

where

$$\phi _{1} (p)=\frac{p^{-1/2}}{2\sqrt{2}}[ \text {cos}(\sqrt{p\eta })+ \text {cos}(\sqrt{p\mu })],$$
(29)
$$\phi _{2} (p)=\text {e}^{-\sqrt{p \mu }} \frac{2 p^{3/2}}{p^{3/2}+\sqrt{2} \tilde{\lambda } p}.$$
(30)

For the inverse Laplace transform of Eq. (29), we use the following formula (see [2], page 106)

$${\mathcal {L}} ^{-1} \left[ p^{-1/2} \text {cos}(\sqrt{p \eta }) \right] ={ \frac{1}{\sqrt{ \pi t}} \text {sin} \left( \frac{\eta }{4t}+{\frac{\pi }{4}} \right) },$$
(31)

and for the inverse Laplace transform of Eq. (30), we use the following formulas (see [1], pages 245–246)

$${\mathcal {L}} ^{-1} \left[ \text {e}^{-\sqrt{p \mu }} \right] ={ \frac{\sqrt{\mu }}{2 \sqrt{ \pi }} t^{-3/2} \text {e}^{-\mu /4t} }, {\text {Re}}(\mu )>0,$$
(32)
$$\begin{aligned}&{\mathcal {L}} ^{-1} \left[ \frac{\text {e}^{-\mu \sqrt{p}}}{ \sqrt{p} + \tilde{\lambda } \sqrt{2} } \right] = \frac{\text {e}^{-\mu ^{2}/4t}}{\sqrt{ \pi t}} \\&-\tilde{\lambda } \sqrt{2} \text {e}^{ \mu \tilde{\lambda } \sqrt{2} +2 \tilde{\lambda } ^{2} t} {\text {erfc}} \left( \frac{\mu }{2 \sqrt{t}}+\tilde{\lambda } \sqrt{2t} \right) , \end{aligned}$$
(33)

where the error function is defined as

$${\text {erfc}}(x) = \frac{2}{\sqrt{\pi }} \int _x^{\infty } \text {e}^{-t^2}\, \text {d}t.$$
(34)

Then, the Green’s function is given by

$$\begin{aligned} G _{\xi } (x,t)= & {} - \int _{0}^{t} \frac{1}{2 \sqrt{ \pi \tau }} \left[ \text {sin} \left( \frac{(x-\xi )^2}{4 \tau }+\frac{\pi }{4} \right) -\text {sin} \left( \frac{(x+\xi )^2}{4 \tau }+\frac{\pi }{4} \right) \right] \text {d} \tau - \int _{0}^{t} \int _{0}^{\tau } \left[ \text {sin} \left( \frac{(x-\xi )^2}{8 (\tau -r)}+\frac{\pi }{4} \right) \right. \\&\left. \quad +\, \text {sin} \left( \frac{(x+\xi )^2}{8 (\tau -r)}+\frac{\pi }{4} \right) \right] \left[ \text {e}^{-(x+\xi )^2 / 8r} \frac{(x+\xi -4 \tilde{\lambda } r)}{4 \pi r \sqrt{r(\tau -r)}} + \frac{2 \tilde{\lambda }^{2}}{\sqrt{2 \pi (\tau -r)} } \text {e}^{ \tilde{\lambda } (x+\xi )+2\tilde{\lambda }^{2} r } {\text {erfc}} \left( \frac{(x+\xi +4 \tilde{\lambda } r)}{2 \sqrt{2r}}\right) \right] \text {d}r \text {d}\tau . \end{aligned}$$
(35)

When we assume that the external loading is nonzero, for example, \(q(x,t)=\delta (x-\xi ) \otimes \delta (t)\), and the initial disturbances are zero (\(u(x,0)=f(x)=0,\,u_{t}(x,0)=g(x)=0\)), the solution for the semi-infinite beam with damping boundary can be written in a non-dimensional form by substituting the following dimensionless quantities in Eq. (35):

$$\begin{aligned}&v=\frac{x}{\xi },\; {s}=\frac{t}{\xi ^{2}},\;\tilde{s}=\frac{\tau }{\xi ^{2}},\; \sigma =\frac{t}{\tau }\;,\varphi =\frac{\tau }{r},\;\tilde{\lambda }=\frac{\lambda }{\xi }, \\&g(v,s)=\frac{G_{\xi }}{\xi }, \end{aligned}$$

we obtain

$$\begin{aligned} g(v,s)= & {} - \int _{1}^{\infty } \frac{\sqrt{s}}{2 \sqrt{ \pi \sigma ^{3}}} \left[ \text {sin} \left( \frac{(v-1)^2 \sigma }{4 s}+\frac{\pi }{4} \right) -\,\text {sin} \left( \frac{(v+1)^2 \sigma }{4 s}+\frac{\pi }{4} \right) \right] \text {d} \sigma - \int _{1}^{\infty } \int _{1}^{\infty } \left[ \text {sin} \left( \frac{\sigma \varphi (v-1)^2}{8s (\varphi -1)}+\frac{\pi }{4} \right) \right. \\&\left. \quad +\, \text {sin} \left( \frac{\sigma \varphi (v+1)^2}{8s (\varphi -1)}+\frac{\pi }{4} \right) \right] \left[ \text {e}^{-\sigma \varphi (v+1)^2 / 8s} \left( \frac{ \sigma \varphi (v+1)-4 {\lambda } s}{4 \pi \sigma ^2 \varphi \sqrt{\varphi -1}}\right) + \frac{ {\lambda }^{2}\sqrt{2 s^3}}{\sqrt{\pi \sigma ^5 \varphi ^3 (\varphi -1)} } \text {e}^{ {\lambda } (v+1)+ \frac{ 2 {\lambda }^{2} s}{ \sigma \varphi } } {\text {erfc}} \left( \frac{\sigma \varphi (v+1)+4 {\lambda } s}{2 \sqrt{2s \sigma \varphi }}\right) \right] \text {d} \varphi \text {d} \sigma . \end{aligned}$$
(36)

Figure 4 shows the shape for the semi-infinite beam with boundary damping during its oscillation. It is observed how the vibration is suppressed due to using a damper (\(\lambda =1\)) at the boundary x = 0.

Fig. 4
figure 4

The Green’s function g(v, s) for a semi-infinite beam with boundary damping (\(\lambda =1\)) for the initial values \(g(v,0)=0,\,g_{s}(v,0)=0\), and the external force \(q(v,s)=\delta (v-1) \otimes \delta (s)\)

Full size image

Figure 5 depicts the Green’s function of the semi-infinite beam for varying boundary damping parameters \({\lambda }\) at s = 0.8. As can be seen, the damping boundary condition starts to behave like free and pinned boundary condition when we take \({\lambda } \rightarrow 0\) and \({\lambda } \rightarrow \infty\), respectively.

For the damping case, we compare our solution in the next section with a long bounded beam by applying the Laplace transform method for a certain value of \(\lambda\).

Fig. 5
figure 5

The Green’s function g(v, s) for a semi-infinite beam with different boundary damping parameters for the initial values \(g(v,0)=0,\,g_{s}(v,0)=0\), and the external force \(q(v,s)=\delta (v-1) \otimes \delta (s)\) at s = 0.8

Full size image

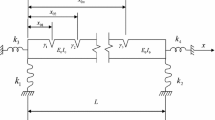
5.2 Damper-clamped ends, \(u_{xxx}(0,t)=-\tilde{\lambda } {u}_{t}(0,t)\), \(u_{xx}(0,t) =u(L,t) = u_{x}(L,t) = 0\)

In this section, we compare our semi-infinite results with results for a bounded domain [0, L] with L large. We can formulate the dimensionless initial boundary value problem describing the transverse vibrations of a damped horizontal beam which is attached to a damper at x = 0 as follows:

$$\ddot{u}(x,t)+u''''(x,t)=q(x,t) ,\quad 0<x<L,\;t>0,$$
(37)
$$u(x,0)=f(x),\quad \dot{u}(x,0)=g(x),\quad 0 \le x<L,$$
(38)

and boundary conditions,

$$\begin{aligned} u^{\prime \prime \prime }(0,t)= & {} -{\lambda } \dot{u}(0,t),\; u^{\prime \prime }(0,t) =0,\quad t\ge 0, \\ u(L,t)= & {} 0,\; u^{\prime }(L,t) = 0, \quad t\ge 0. \end{aligned}$$
(39)

We will also solve this problem by using the Laplace transform method which reduces the partial differential equation Eq. (37) to a non-homogeneous linear ordinary differential equation, which can be solved by using standard techniques [5, 11]. When we apply the Laplace transform method, which was defined in Eq. (9), to Eqs. (37)–(39), we obtain the following boundary value problem

$$\text {PDE:}\;U^{\prime \prime \prime \prime }(x,p)+p^{2}U(x,p)=Q(x,p),$$
(40)
$$\begin{aligned}\text {BCs:}&\;U^{\prime \prime \prime }(0,p)=-{\lambda }[pU(0,p)-f(0)], \\&U^{\prime \prime }(0,t) =0,\;U(L,p) =0,\; U^{\prime }(L,p) = 0, \end{aligned}$$
(41)

where U(x, p) and Q(x, p) are the Laplace transforms of u(x, t) and q(x, t), and p is the transform variable. Here, \(Q(x,p)=\delta (x-\xi )+p\,u(x,0)+\dot{u}(x,0)\). We assume that the initial conditions are zero, that is \(u(x,0)=f(x)=0\) and \(\dot{u}(x,0)=g(x)=0\).

The general solution of the homogeneous equation, that is, Eq. (40) with \(Q(x,p)=0\), is given by

$$\begin{aligned} U(x,\beta )= & {}\, C_{1}(\beta )\cos (\beta x)+ C_{2}(\beta )\sin (\beta x) \\&\quad +\,C_{3}(\beta )\cosh (\beta x)+C_{4}(\beta )\sinh (\beta x), \end{aligned}$$
(42)

where \(C_{j}(\beta )\) are arbitrary functions for \(j=1\ldots 4\). For simplicity, we consider \(p^{2}=-\beta ^{4}\), so that \(p=\mp i \beta ^{2}\). We consider only the case \(p= i \beta ^{2}\) for further calculations, because the case \(p=-i \beta ^{2}\) will also lead to the same p.

The particular solution of the non-homogeneous equation Eq. (40) can be defined by using the method of variation of parameters. We rewrite the general solution as follows:

$$\begin{aligned} U(x,\beta )= & {} \,K_{1}(\beta )\cos (\beta x)+ K_{2}(\beta )\sin (\beta x) \\&\quad +\,K_{3}(\beta )\cosh (\beta x)+K_{4}(\beta )\sinh (\beta x) \\&\quad +\,{\frac{1}{2\beta ^{3}}} \int ^{x}_{0} Q(s,\beta )[\sin (\beta (s-x))-\sinh (\beta (s-x))]\text {d}s, \end{aligned}$$
(43)

where \(Q(s,\beta )=\delta (s-\xi )\). \(K_{j}(\beta )\) for \(j=1\ldots 4\) can be determined from the boundary conditions and the solution of Eqs. (40) and (41) is given by

$$\begin{aligned} U(x,\beta )=&\int ^{L}_{0} Q(s,\beta )H_{1}(s,\beta :x)\text {d}s \\&+ \int ^{x}_{0} Q(s,\beta )H_{2}(s,\beta :x)\text {d}s, \end{aligned}$$
(44)

where

$$\begin{aligned} H_{1}(s,\beta :x):= & {} \frac{1}{4 \beta ^{3} h_{\lambda L}(\beta )} [\varTheta _{1}(x)\varUpsilon _{1}(s,\beta ) \\&\quad +\,\varTheta _{2}(x)\varUpsilon _{2}(s,\beta )+\varTheta _{3}(x)\varUpsilon _{3}(s,\beta )] , \end{aligned}$$
(45)
$$\varTheta _{1}(x):= \cos (\beta x)+\cosh (\beta x),$$
(46)
$$\begin{aligned} \varUpsilon _{1}(s,\beta ):= & {} [\sin (\beta (L-s))-\sinh (\beta (L-s))] \\&\quad \beta [\cos (\beta L)+\cosh (\beta L)] \\&\quad -\,[\cos (\beta (L-s))-\cosh (\beta (L-s))] \\&\quad \beta [\sin (\beta L)+\sinh (\beta L)], \end{aligned}$$
(47)
$$\varTheta _{2}(x):= \sin (\beta x),$$
(48)
$$\begin{aligned} \varUpsilon _{2}(s,\beta ):= & {} [\sin (\beta (L-s))-\sinh (\beta (L-s))] \\&\quad [2 \lambda i \cosh (\beta L)+\beta (\sin (\beta L)-\sinh (\beta L))] \\&\quad -\,[\cos (\beta (L-s))-\cosh (\beta (L-s))] \\&\quad [2 \lambda i \sinh (\beta L)-\beta (\cos (\beta L)+\cosh (\beta L))], \end{aligned}$$
(49)
$$\varTheta _{3}(x):= \sinh (\beta x),$$
(50)
$$\begin{aligned} \varUpsilon _{3}(s,\beta ):= & {} [\sin (\beta (L-s))-\sinh (\beta (L-s))] \\&\quad [2 \lambda i \cos (\beta L)-\beta (\sin (\beta L)-\sinh (\beta L))] \\&\quad -\,[\cos (\beta (L-s))-\cosh (\beta (L-s))] \\&\quad [2 \lambda i \sin (\beta L)+\beta (\cos (\beta L)+\cosh (\beta L))], \end{aligned}$$
(51)
$$\begin{aligned} h_{\lambda L}(\beta ):& = \beta [1+\cos (\beta L)\cosh (\beta L)] \\&\quad +\, \lambda i [\cosh (\beta L) \sin (\beta L)-\sinh (\beta L) \cos (\beta L)], \end{aligned}$$
(52)
$$H_{2}(s,\beta :x):=\, {\frac{1}{2 \beta ^{3}}}[\sin (\beta (s-x))-\sinh (\beta (s-x))],$$
(53)

In order to obtain the solution of Eqs. (37)–(39), the inverse Laplace transform of U(x, p) will be applied by using Cauchy’s residue theorem, that is,

$$\begin{aligned} u(x,t)&={\frac{1}{2 \pi i }}\int _{\gamma -i\infty }^{\gamma +i\infty } \text {e}^{pt} U (x,p) \text {d}p, \\&= \sum _{n} \text {Res}(\text {e}^{pt}U(x,p),\,p= p_{n}), \end{aligned}$$
(54)

for \(\gamma > 0\). Here \(\text {Res}(\text {e}^{pt}U(x,p),\,p= p_{n})\) is the residue of \(\text {e}^{pt}U(x,p)\) at the isolated singularity at \(p=p_{n}\). The poles of U(x, p) are determined by the roots of the following characteristic equation

$$h_{\lambda L}(\beta ):=0,$$
(55)

which is a ”transcendental equation” defined in Eq. (52). The zeros of \(h_{\lambda L}(\beta )\) for \(\lambda =0\), which reduces the problem to the clamped-free beam, have been considered in [15]. By using Rouché’s theorem, it can be shown that the number of roots of \(h_{\lambda L}(\beta ):=0\) (\(\lambda >0\)) is equal to the same number of roots of \(h_{ L}(\beta ):=0\) (\(\lambda =0\)). For the proof of Rouché’s theorem, the reader is refered to Ref. [4]. Equation (55) has infinitely many roots [18]. By using the relation \(p=i \beta ^{2}\), we can determine the roots of p, which are defined in complex conjugate pairs, such that \(p_{n}=p_{n}^{re}\mp i p_{n}^{im}\), where \(n\in {\mathbb {N}}\) and \(p_{n}^{re},\, p_{n}^{im}\in {\mathbb {R}}\). So, the damping rate and oscillation rate are given by \(p_{n}^{re}:=-2 \beta _{n}^{re}\beta _{n}^{im}\) and \(p_{n}^{im}:=(\beta _{n}^{re})^2-(\beta _{n}^{im})^2\), respectively.

In order to construct asymptotic approximations of the roots of \(h_{\lambda L}(\beta )\), we first multiply Eq. (55) by L, and define \(\tilde{\beta }=\beta L\) and \(\tilde{\lambda }=\lambda L\). Hence, we obtain

$$\begin{aligned} h_{\tilde{\lambda } }(\tilde{\beta })&\equiv \tilde{\beta } [1+\cos (\tilde{\beta })\cosh (\tilde{\beta })] \\&\quad + \tilde{\lambda } i [\cosh (\tilde{\beta }) \sin (\tilde{\beta })-\sinh (\tilde{\beta }) \cos (\tilde{\beta })]=0. \end{aligned}$$
(56)

Next, multiplying \(h_{\tilde{\lambda } }(\tilde{\beta })\) by \(({2})/({\tilde{\beta } \,\text {e}^{\tilde{\beta }}})\), the characteristic equation yields

$$\cos ({\tilde{\beta } })={\mathcal {O}}(|\tilde{\beta } |^{-2})+i \left( \frac{\tilde{\lambda } }{\tilde{\beta } }\left[ \cos (\tilde{\beta })-\sin (\tilde{\beta })\right] + {\mathcal {O}}(|\tilde{\beta } |^{-3}) \right) ,$$
(57)

or

$$\cos ({\tilde{\beta } })={\mathcal {O}}(|\tilde{\beta } |^{-1}),$$
(58)

which is valid in a small neighbourhood of \(k=(n-\frac{1}{2})\) for all \(n>0\). After applying Rouché’s theorem (see [6]), the following asymptotic solutions for \(\beta _{n}\) and \(p_{n}\) are obtained

$$\beta _{n}=\mp \frac{1}{L} \left[ k\pi +{\mathcal {O}}(|n |^{-2}) +i \left( \frac{\lambda L}{k\pi }+{\mathcal {O}}(|n |^{-2})\right) \right] ,$$
(59)
$$p_{n}= \frac{-2 \lambda }{L}+ {\mathcal {O}}(|n |^{-1}) +i \left( \frac{(k\pi )^4-(\lambda L)^2}{(k L \pi )^2}+{\mathcal {O}}(|n |^{-1})\right) ,$$
(60)

which are valid and represent the asymptotic approximations of the damping rates of the eigenvalues for sufficiently large \(n\in {\mathbb {N}}\).

The first twenty roots \(\beta _{num,n}\) and \(p_{num,n}\), which are computed numerically by using Maple, and the first twenty asymptotic approximations of the roots of the Eq. (55) are listed in Table 2. For higher modes, it is found that the asymptotic and numerical approximations of the damping rates are very close to each other, and the numerical damping rates, which are the real part of \(p_{num,n}\), converges to −0.2.

Table 2 Numerical approximations of the solutions \(\beta _{n}\) and \(p_{n}\) of the characteristic equation Eq. (55) for the case \(L=10\) and \(\lambda =1\)
Full size table

The characteristic equation Eq. (55) has three unique real-valued roots; p = 0 is one of these roots. Note that p = 0 is not a pole of U(x, p). That is why, the only contribution to the inverse Laplace transform is the first integral of Eq. (44). The implicit solution of the problem Eqs. (37)–(39) is given by

$$\begin{aligned} u(x,t)&=\,\text {e}^{p_{-1}t}H(x,p_{-1})+\text {e}^{p_{0}t}H(x,p_{0}) \\&\quad +\sum _{n=1}^{N} \text {e}^{p_{n}^{re}t}\left( \left[ H(x,p_{n})+\overline{H(x,p_{n})}\right] \cos \left( p_{n}^{im}t\right) \right. \\&\left. \quad +\,i\left[ H(x,p_{n})-\overline{H(x,p_{n})}\right] \sin \left( p_{n}^{im}t\right) \right) , \end{aligned}$$
(61)

where \(\overline{H(x,p_{n})}\) is the complex conjugate of \({H(x,p_{n})}\), and \({H(x,p_{n})}\) is given by

$${H(x,p_{n})}:=\frac{R(x,p_{n})}{\partial _{p}{(\varOmega (p_{n}))|_{p=p_{n}}} },$$
(62)

where

$$\begin{aligned} {R(x,p_{n})}:=&\,[\varTheta _{1}(x)\varUpsilon _{1}(s,\beta _{n})+\varTheta _{2}(x)\varUpsilon _{2}(s,\beta _{n}) \\&+\,\varTheta _{3}(x)\varUpsilon _{3}(s,\beta _{n})], \end{aligned}$$
(63)
$${\partial _{p}{(\varOmega (p_{n}))|_{p=p_{n}}} }=\left( \frac{\partial {\varOmega (\beta _{n})}}{\partial _{\beta _{n}}} \frac{\partial _{\beta _{n}}}{\partial _{p_{n}}} \right),$$
(64)
$$\varOmega (\beta _{n}):= 4 \beta _{n}^{3}\, h_{\lambda L}(\beta _{n}).$$
(65)

By using the relation \(p_{n}=i \beta _{n}^{2}\), \(\beta _{n}:=\beta _{n}^{re}+i \beta _{n}^{im}\) is defined by

$$\beta _{n}^{re}=\frac{\sqrt{p_{n}^{im}+\sqrt{(p_{n}^{re})^2+(p_{n}^{im})^2}}}{\sqrt{2}},$$
(66)

and

$$\beta _{n}^{im}=\frac{-p_{n}^{re} \sqrt{2}}{2\sqrt{p_{n}^{im}+\sqrt{(p_{n}^{re})^2+(p_{n}^{im})^2}}}.$$
(67)

The numerical approximations of the roots which are listed in Table 2 can be substituted into Eq. (61) to obtain explicit approximations of the problem Eqs. (37)–(39). Figure 6 shows the comparison of the numerical and exact solutions of a damper-clamped ended finite beam (L = 10) and a damper ended semi-infinite beam with \(\lambda =1\) for the zero initial values and the external force \(q(x,t)=\delta (x-1)\otimes \delta (t)\) at times t = 0.4 and t = 0.8. It can be seen that the numerical results in Fig. 6a, b are similar to the analytical (exact) results in Fig. 6c when the number of modes become sufficiently large.

Fig. 6
figure 6

The comparison of the numerical and exact solutions of a damper-clamped ended finite beam (L = 10) and a damper ended semi-infinite beam with \(\lambda =1\) for the zero initial values and the external force \(q(x,t)=\delta (x-1) \otimes \delta (t)\) at times t = 0.4 and t = 0.8. a The first ten oscillation modes as approximation of the solution of u(x, t) for a damper-clamped ended finite beam, b the first forty oscillation modes as approximation of the solution of u(x, t) for a damper-clamped ended finite beam, c the Green’s function g(v, s) for a one-sided damper ended semi-infinite beam

Full size image

6 The energy in the damped case

In this section, we derive the energy of the transversally free vibrating homogeneous semi-infinite beam (q = 0)

$$\ddot{u}(x,t)+u^{\prime \prime \prime \prime }(x,t)=0 ,\quad 0<x<\infty ,\quad t>0,$$
(68)

subject to the boundary conditions \(u_{xx}(0,t) = 0\), and \(u_{xxx}(0,t)=-\tilde{\lambda } {u}_{t}(0,t)\). By multiplying Eq. (68) with \(\dot{u}\), we obtain the following expression

$$\left\{ {1 \over 2}\,(\dot{u}^2+u^{\prime \prime 2})\right\} _{t}+\{\dot{u} u^{\prime \prime \prime }+\dot{u}^{\prime } u^{\prime \prime }\}_{x}=0 ,$$
(69)

By integrating Eq. (69) with respect to x from x = 0 to \(x=\infty\) and with respect to t from t = 0 to t = t, respectively, we obtain the total mechanical energy E(t) in the interval \((0,\infty )\). This energy E(t) is the sum of the kinetic and the potential energy of the beam, that is,

$$E(t)={1 \over 2}\int ^{\infty }_{0}(\dot{u}^2+u''\,^2)\text {d}x.$$
(70)

The time derivative of the energy E(t) is given by

$$\dot{E}(t)=-\tilde{\lambda } \dot{u}^2(0,t),$$
(71)

where \(\tilde{\lambda }\) is the boundary damping parameter. And so, it follows from Eq. (71) that :

$$E(t)=E(0)-{\tilde{\lambda }} \,\int ^{t}_{0}{u_{s}}^2(0,s)\text {d}s.$$
(72)

When the damping parameter \(\tilde{\lambda }>0\), it follows from Eq. (72) that energy of the system is dissipated. If \(\tilde{\lambda }=0\), then \(E(t)=E(0)\), which represents conservation of energy.

7 Conclusion

In this paper, an initial-boundary value problem for a beam equation on a semi-infinite interval has been studied. We applied the method of Laplace transforms to obtain the Green’s function for a transversally vibrating homogeneous semi-infinite beam, and examined the solution for various boundary conditions. In order to validate our analytical results, explicit numerical approximations of the damping and oscillating rates were constructed by using the Laplace transform method to finite domain. It has been shown that the numerical results approach the exact results for sufficiently large domain length and for sufficiently many number of modes. The total mechanical energy and its time-rate of change can also be derived.

This paper provides an understanding of how the Green’s function for a semi-infinite beam can be calculated analytically for (non)-classical boundary conditions. The method as given in this paper can be used for other boundary conditions as well.