Study of non-uniform viscoelastic nanoplates vibration based on nonlocal first-order shear deformation theory

Abstract

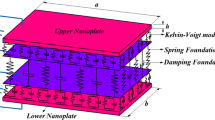
In this paper, vibration features of variable thickness rectangular viscoelastic nanoplates are studied. In order to consider the small-scale and the transverse shear deformation effects, governing differential equations and relevant boundary conditions are adopted based on the nonlocal elasticity theory in relation to first-order shear deformation theory of plates. The numerical solution for the nanoplate vibration frequencies is proposed applying the differential quadrature method, as a simple, effective and precise numerical tool. The present formulation and solution method are validated showing their fast convergence rate and comparison of results, in limited cases, using the available literature. Excellent agreement between the obtained and available results is observed. The effects of structural damping coefficient, boundary conditions, aspect ratio, nonlocal and variable thickness parameters on viscoelastic nanoplates vibration behaviour are studied in detail.

Appendices

Appendix 1: DQM brief view

Consider a continuous function f(x, y) consists of two different coordinates x and y. Based on DQM, the rth order derivative of f relative to x and the (r + s)th order derivative of f with respect to x and y are estimated as [39, 40]

$$\begin{aligned} \left. {\frac{{\partial^{r} f}}{{\partial x^{r} }}} \right|_{{(x_{i} ,y_{j} )}} & = \sum\limits_{m = 1}^{{N_{x} }} {A_{im}^{(r)} f(x_{m} ,y_{j} )} = \sum\limits_{m = 1}^{{N_{x} }} {A_{im}^{(r)} f_{mj} } , \\ \left. {\frac{{\partial^{(r + s)} f}}{{\partial x^{r} \partial y^{s} }}} \right|_{{(x_{i} ,y_{j} )}} & = \sum\limits_{n = 1}^{{N_{y} }} {\sum\limits_{m = 1}^{{N_{x} }} {A_{im}^{(r)} \bar{A}_{jn}^{(s)} f(x_{m} ,y_{n} )} } = \sum\limits_{n = 1}^{{N_{y} }} {\sum\limits_{m = 1}^{{N_{x} }} {A_{im}^{(r)} \bar{A}_{jn}^{(s)} f_{mn} } } \\ \end{aligned}$$

(38a, b)

where N _x and N _y are the number of grid points along the x and y-directions, respectively. $A_{ij}^{(r)}$ and $\bar{A}_{ij}^{(r)}$ express weight coefficients relevant to the rth order derivative in the x- and y-directions, respectively. Based on the law of Shu [40], the weight coefficients in the ξ-direction (ξ = x or y) are determined as follows.

If r = 1, i.e., for the 1st order derivative,

$$A_{ij}^{(1)} = \frac{{M^{(1)} (\xi_{i} )}}{{(\xi_{i} - \xi_{j} )M^{(1)} (\xi_{j} )}}\quad \, for\quad i \ne j\quad and\quad \, i,j = 1,2, \ldots ,N_{\xi }$$

(39)

and

$$A_{ii}^{(1)} = - \sum\limits_{j = 1(j \ne i)}^{{N_{\xi } }} {A_{ij}^{(1)} } \quad \, for\quad i = j\quad and\quad i = 1,2, \ldots ,N_{\xi }$$

(40)

where $M^{(1)} (\xi_{i} )$ is the 1st order derivative of $M(\xi_{i} )$, expressed as follows

$$M(\xi ) = \prod\limits_{j = 1}^{{N_{\xi } }} {(\xi - \xi_{j} )} , \, M^{(1)} (\xi_{k} ) = \prod\limits_{j = 1(j \ne k)}^{{N_{\xi } }} {(\xi_{k} - \xi_{j} )}$$

(41a, b)

If r = 2, i.e., for the 2nd order derivative,

$$A_{ij}^{(2)} = 2A_{ij}^{(1)} \left( {A_{ii}^{(1)} - \frac{1}{{\xi_{i} - \xi_{j} }}} \right)\quad for\quad i \ne j\quad and\quad i,j = 1,2, \ldots ,N_{\xi }$$

(42)

and

$$A_{ii}^{(2)} = - \sum\limits_{j = 1(j \ne i)}^{{N_{\xi } }} {A_{ij}^{(2)} } \quad for\quad i = 1,2, \ldots ,N_{\xi }$$

(43)

If r > 2, i.e., for the higher order derivatives, the weight coefficients are determined via the following simple recursive ratios

$$A_{ij}^{(3)} = \sum\limits_{k = 1}^{{N_{\xi } }} {A_{ik}^{(1)} } A_{kj}^{(2)} ,\quad A_{ij}^{(4)} = \sum\limits_{k = 1}^{{N_{\xi } }} {A_{ik}^{(1)} } A_{kj}^{(3)} \quad for\quad i,j = 1,2, \ldots N_{\xi }$$

(44a, b)

An important item in the application of DQM, is the mode of grid points selection. It has been shown that the grid point distribution, which is based on the well accepted Gauss–Chebyshev–Lobatto points [40], provides sufficient and precise results. According to this grid point’s distribution, the grid point’s coordinates are as follows

$$\begin{aligned} \xi_{i} & = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\pi \left( {i - 1} \right)}}{{N_{\xi } - 1}}} \right]} \right\}, \quad i = 1,2, \ldots ,N_{\xi } \\ \eta_{j} & = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\pi \left( {j - 1} \right)}}{{N_{\eta } - 1}}} \right]} \right\},\quad j = 1,2, \ldots ,N_{\eta } \, \\ \end{aligned}$$

(45a, b)

Appendix 2: Exact solution for uniform viscoelastic nanoplates

For constant-thickness viscoelastic nanoplates with fully simply supported edges, one may derive the nonlocal equations of motion as follows

$$\begin{aligned} & \frac{{\partial^{2} \psi^{x} }}{{\partial \xi^{2} }} + \chi \left( {Q_{12} + Q_{33} } \right)\frac{{\partial^{2} \psi^{y} }}{\partial \xi \partial \eta } + \chi^{2} Q_{33} \frac{{\partial^{2} \psi^{x} }}{{\partial \eta^{2} }} - Q_{44} \left( {\psi^{x} + \frac{\partial W}{\partial \xi }} \right) \\ & \quad +\, \frac{{\Omega^{2} }}{{1 + ig^{ * } \Omega }}\left[ {\psi^{x} - \gamma^{2} \left( {\frac{{\partial^{2} \psi^{x} }}{{\partial \xi^{2} }} + \chi^{2} \frac{{\partial^{2} \psi^{x} }}{{\partial \eta^{2} }}} \right)} \right] = 0 \\ \end{aligned}$$

(46)

$$\begin{aligned} & Q_{33} \frac{{\partial^{2} \psi^{y} }}{{\partial \xi^{2} }} + \chi \left( {Q_{12} + Q_{33} } \right)\frac{{\partial^{2} \psi^{x} }}{\partial \xi \partial \eta } + \chi^{2} Q_{22} \frac{{\partial^{2} \psi^{y} }}{{\partial \eta^{2} }} - Q_{55} \left( {\psi^{y} + \chi \frac{\partial W}{\partial \eta }} \right) \\ & \quad +\, \frac{{\Omega^{2} }}{{1 + ig^{ * } \Omega }}\left[ {\psi^{y} - \gamma^{2} \left( {\frac{{\partial^{2} \psi^{y} }}{{\partial \xi^{2} }} + \chi^{2} \frac{{\partial^{2} \psi^{y} }}{{\partial \eta^{2} }}} \right)} \right] = 0 \\ \end{aligned}$$

(47)

$$Q_{44} \left( {\frac{{\partial \psi^{x} }}{\partial \xi } + \frac{{\partial^{2} W}}{{\partial \xi^{2} }}} \right) + \chi Q_{55} \left( {\frac{{\partial \psi^{y} }}{\partial \eta } + \chi \frac{{\partial^{2} W}}{{\partial \eta^{2} }}} \right) + \frac{{\bar{I}\Omega^{2} }}{{1 + ig^{ * } \Omega }}\left[ {W - \gamma^{2} \left( {\frac{{\partial^{2} W}}{{\partial \xi^{2} }} + \chi^{2} \frac{{\partial^{2} W}}{{\partial \eta^{2} }}} \right)} \right] = 0$$

(48)

Employing the Navier method, the solution of the above equations can be written as

$$\begin{aligned} W & = \sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 1}^{\infty } {\bar{W}_{mn} \sin \left( {m\pi \xi } \right)\sin \left( {n\pi \eta } \right)} } \\ \psi^{x} & = \sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 1}^{\infty } {\bar{\psi }_{mn}^{x} \cos \left( {m\pi \xi } \right)\sin \left( {n\pi \eta } \right)} } \\ \psi^{y} & = \sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 1}^{\infty } {\bar{\psi }_{mn}^{y} \sin \left( {m\pi \xi } \right)\cos \left( {n\pi \eta } \right)} } \\ \end{aligned}$$

(49a{-}c)

Substituting for W, $\psi^{x}$ and $\psi^{y}$ from Eq. (49) into Eqs. (46)–(48), yields

$$\left( {\left[ {\begin{array}{*{20}l} {\Theta_{11} } &\quad {\Theta_{12} } &\quad {\Theta_{13} } \\ {\Theta_{21} } &\quad {\Theta_{22} } &\quad {\Theta_{23} } \\ {\Theta_{31} } &\quad {\Theta_{32} } &\quad {\Theta_{33} } \\ \end{array} } \right] - \bar{\Omega }\left[ {\begin{array}{*{20}l} {\Xi_{11} } &\quad 0 & \quad 0 \\ 0 & \quad {\Xi_{22} } & \quad 0 \\ 0 & \quad 0 & \quad {\Xi_{33} } \\ \end{array} } \right]} \right)\left\{ {\begin{array}{*{20}l} {\bar{\psi }_{mn}^{x} } \\ {\bar{\psi }_{mn}^{y} } \\ {\bar{W}_{mn} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$

(50)

where

$$\begin{aligned} \Theta_{11} & = Q_{44} + \left( {m\pi } \right)^{2} + \left( {n\pi } \right)^{2} \chi^{2} Q_{33} ,\,\Theta_{22} = Q_{55} + \left( {m\pi } \right)^{2} Q_{33} + \left( {n\pi } \right)^{2} \chi^{2} Q_{22} , \\ \Theta_{33} & = \left( {m\pi } \right)^{2} Q_{44} + \left( {n\pi } \right)^{2} \chi^{2} Q_{55} ,\,\Theta_{21} = \Theta_{12} = nm\pi^{2} \chi \left( {Q_{12} + Q_{33} } \right), \\ \Theta_{31} & = \Theta_{13} = m\pi Q_{44} ,\;\Theta_{32} = \Theta_{23} = n\pi \chi Q_{55} ,\;\Xi_{11} = \Xi_{22} = 1 + \gamma^{2} \left[ {\left( {m\pi } \right)^{2} + \left( {n\pi } \right)^{2} \chi^{2} } \right], \\ \Xi_{33} & = \bar{I}\Xi_{11} = \bar{I}\left\{ {1 + \gamma^{2} \left[ {\left( {m\pi } \right)^{2} + \left( {n\pi } \right)^{2} \chi^{2} } \right]} \right\} \\ \end{aligned}$$

(51a{-}h)

in which $\bar{\Omega }$ is defined by $\bar{\Omega } = {{\Omega^{2} } \mathord{\left/ {\vphantom {{\Omega^{2} } {\left( {1 + ig^{ * } \Omega } \right)}}} \right. \kern-0pt} {\left( {1 + ig^{ * } \Omega } \right)}}.$ The non-dimensional eigenfrequency $(\varpi = i\Omega )$ can be written as

$$\varpi = - \frac{{g^{ * } \bar{\Omega }}}{2} \pm i\sqrt {\bar{\Omega } - \left( {\frac{{g^{ * } \bar{\Omega }}}{2}} \right)^{2} } = - \omega_{n} \left( {\zeta \pm i\sqrt {1 - \zeta^{2} } } \right)$$

(52)

The dimensionless frequency of undamped vibration $(\omega_{n} )$ and the damping ratio $(\zeta )$ are expressed as

$$\omega_{n} = \sqrt {\bar{\Omega }} , \quad \zeta = \frac{1}{2}g^{ * } \sqrt {\bar{\Omega }}$$

(53a, b)