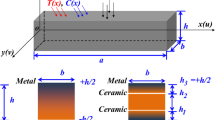
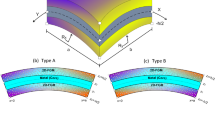
Appendix
The matrices in Eq. (25) are written as
$$ {\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{pp} } & 0 & 0 & 0 & 0 \\ 0 & {{\mathbf{M}}_{rr} } & 0 & 0 & 0 \\ 0 & 0 & {{\mathbf{M}}_{gg} } & 0 & {{\mathbf{M}}_{gq} } \\ 0 & 0 & 0 & {{\mathbf{M}}_{ff} } & {{\mathbf{M}}_{fq} } \\ 0 & 0 & {{\mathbf{M}}_{qg} } & {{\mathbf{M}}_{qf} } & {{\mathbf{M}}_{qq} } \\ \end{array} } \right], $$
(28)
where
$$ {\mathbf{M}}_{pp} = \left( {\rho_{f} h_{f} + \frac{{\rho_{c} h_{c} }}{2}} \right)\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upxi \upxi }}^{\text{T}} {\text{d}}x{\text{d}}y} } , $$
(29)
$$ {\mathbf{M}}_{rr} = \left( {\rho_{f} h_{f} + \frac{{\rho_{c} h_{c} }}{2}} \right)\int_{0}^{a} {\int_{0}^{b} {{\mathbf{\varsigma \varsigma }}^{\text{T}} {\text{d}}x{\text{d}}y} } , $$
(30)
$$ {\mathbf{M}}_{gg} = \left( {\frac{{\rho_{f} h_{f} h_{c}^{2} }}{4} + \frac{{\rho_{c} h_{c}^{3} }}{24}} \right)\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upchi \upchi }}^{\text{T}} {\text{d}}x{\text{d}}y} }, {\mathbf{M}}_{gq} = \frac{{\rho_{f} h_{c} h_{f}^{2} }}{2}\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upchi}}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } , $$
(31)
$$ {\mathbf{M}}_{ff} = \left( {\frac{{\rho_{f} h_{f} h_{c}^{2} }}{4} + \frac{{\rho_{c} h_{c}^{3} }}{24}} \right)\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upeta \upeta }}^{\text{T}} {\text{d}}x{\text{d}}y} } ,{\mathbf{M}}_{gq} = \frac{{\rho_{f} h_{c} h_{f}^{2} }}{2}\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upeta}}\frac{{\partial {\varvec{\upzeta}}}}{\partial y}^{\text{T}} {\text{d}}x{\text{d}}y} } , $$
(32)
$$ {\mathbf{M}}_{qq} = \left( {\rho_{f} h_{f} + \frac{{\rho_{c} h_{c} }}{2}} \right)\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upzeta \upzeta }}^{\text{T}} {\text{d}}x{\text{d}}y} } + \frac{{\rho_{f} h_{f}^{3} }}{3}\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial {\varvec{\upzeta}}}}{\partial x}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x} + \frac{{\partial {\varvec{\upzeta}}}}{\partial y}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial y}} \right){\text{d}}x{\text{d}}y} } , $$
(33)
$$ {\mathbf{M}}_{qg} = {\mathbf{M}}_{gq}^{\text{T}} ,{\mathbf{M}}_{qf} = {\mathbf{M}}_{fq}^{\text{T}} . $$
(34)
$$ {\mathbf{C}}_{\Delta p} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{C}}_{qq} } \\ \end{array} } \right], $$
(35)
where
$$ {\mathbf{C}}_{qq} = \frac{{\gamma p_{\infty } M_{\infty }^{2} }}{{\sqrt {M_{\infty }^{2} - 1} }}\frac{{M_{\infty }^{2} - 2}}{{M_{\infty }^{2} - 1}}\frac{1}{{U_{\infty } }}\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upzeta \upzeta }}^{\text{T}} {\text{d}}x{\text{d}}y} } . $$
(36)
$$ {\mathbf{K}}_{\Delta p} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{K}}_{\Delta p}^{qq} } \\ \end{array} } \right], $$
(37)
where
$$ {\mathbf{K}}_{\Delta p}^{qq} = \frac{{\gamma p_{\infty } M_{\infty }^{2} }}{{\sqrt {M_{\infty }^{2} - 1} }}\int_{0}^{a} {\int_{0}^{b} {{\varvec{\upzeta}}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } . $$
(38)
$$ {\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{pp} } & {{\mathbf{K}}_{pr} } & {{\mathbf{K}}_{pg} } & {{\mathbf{K}}_{pf} } & {{\mathbf{K}}_{pq} } \\ {{\mathbf{K}}_{rp} } & {{\mathbf{K}}_{rr} } & {{\mathbf{K}}_{rg} } & {{\mathbf{K}}_{rf} } & {{\mathbf{K}}_{rq} } \\ {{\mathbf{K}}_{gp} } & {{\mathbf{K}}_{gr} } & {{\mathbf{K}}_{gg} } & {{\mathbf{K}}_{gf} } & {{\mathbf{K}}_{gq} } \\ {{\mathbf{K}}_{fp} } & {{\mathbf{K}}_{fr} } & {{\mathbf{K}}_{fg} } & {{\mathbf{K}}_{ff} } & {{\mathbf{K}}_{fq} } \\ {{\mathbf{K}}_{qp} } & {{\mathbf{K}}_{qr} } & {{\mathbf{K}}_{qg} } & {{\mathbf{K}}_{qf} } & {{\mathbf{K}}_{qq} } \\ \end{array} } \right], $$
(39)
where
$$ \begin{aligned} K_{pp} & = (h_{c} Q_{c11} + A_{t11} + A_{b11} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial \xi^{T} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad+ (h_{c} Q_{c66} + A_{t66} + A_{b66} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial \xi^{T} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + (A_{t16} + A_{b16} )\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{\partial \xi }{\partial x}\frac{{\partial \xi^{T} }}{\partial y} + \frac{\partial \xi }{\partial y}\frac{{\partial \xi^{T} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } \\ \end{aligned} $$
(40)
$$ \begin{aligned} K_{pr} & = (A_{t16} + A_{b16} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial \varsigma^{T} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + (h_{c} Q_{c12} + A_{t12} + A_{b12} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial \varsigma^{T} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + (A_{t26} + A_{b26} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial \varsigma^{T} }}{\partial y}{\text{d}}x{\text{d}}y} }\\ & \quad + (h_{c} Q_{c66} + A_{t66} + A_{b66} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial \varsigma^{T} }}{\partial x}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(41)
$$ \begin{aligned} K_{pg} & = \frac{{h_{c} }}{2}(A_{b11} - A_{t11} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial {\varvec{\upchi}}^{T} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}(A_{b16} - A_{t16} )\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{\partial \xi }{\partial x}\frac{{\partial {\varvec{\upchi}}^{T} }}{\partial y} + \frac{\partial \xi }{\partial y}\frac{{\partial {\varvec{\upchi}}^{T} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}(A_{b66} - A_{t66} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial {\varvec{\upchi}}^{T} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(42)
$$ \begin{aligned} K_{pf} & = \frac{{h_{c} }}{2}(A_{b16} - A_{t16} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial {\varvec{\upeta}}^{T} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ &\quad + \frac{{h_{c} }}{2}(A_{b12} - A_{t12} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial {\varvec{\upeta}}^{T} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ &\quad + \frac{{h_{c} }}{2}(A_{b66} - A_{t66} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial {\varvec{\upeta}}^{T} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}(A_{b26} - A_{t26} )\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial {\varvec{\upeta}}^{T} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(43)
$$ \begin{aligned} {\mathbf{K}}_{pq} & = \left[ {\frac{{h_{c} (A_{t11} - A_{b11} )}}{2} - B_{b11} - B_{t11} } \right]\\ &\quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial^{2} \zeta^{T} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {\frac{{h_{c} (A_{t26} - A_{b26} )}}{2} - B_{b26} - B_{t26} } \right] \\ &\quad \times\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial^{2} \zeta^{T} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {\frac{{h_{c} (A_{t12} - A_{b12} )}}{2} - B_{b12} - B_{t12} } \right] \\ &\quad \times\int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial^{2} \zeta^{T} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {\frac{{h_{c} (A_{t16} - A_{b16} )}}{2} - B_{b16} - B_{t16} } \right] \\ &\quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial^{2} \zeta^{T} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + [h_{c} (A_{t66} - A_{b66} ) - 2(B_{b66} + B_{t66} )] \\ &\quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial y}\frac{{\partial^{2} \zeta^{T} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + [h_{c} (A_{t16} - A_{b16} ) - 2(B_{b16} + B_{t16} )] \\ &\quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{\partial \xi }{\partial x}\frac{{\partial^{2} \zeta^{T} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(44)
$$ \begin{aligned} {\mathbf{K}}_{rr} & = (h_{c} Q_{c66} + A_{t66} + A_{b66} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial {\mathbf{\varsigma }}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad+ (A_{t26} + A_{b26} )\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial {\varvec{\upxi}}}}{\partial x}\frac{{\partial {\varvec{\upxi}}^{\text{T}} }}{\partial y} + \frac{{\partial {\varvec{\upxi}}}}{\partial y}\frac{{\partial {\varvec{\upxi}}^{\text{T}} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } \\ & \quad + (h_{c} Q_{c22} + A_{t22} + A_{b22} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upxi}}}}{\partial y}\frac{{\partial {\varvec{\upxi}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(45)
$$ \begin{aligned} {\mathbf{K}}_{rg} & = \frac{{h_{c} }}{2}(A_{b16} - A_{t16} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y}} \\ & \quad + \frac{{h_{c} }}{2}(A_{b66} - A_{t66} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}(A_{b12} - A_{t12} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y}} \\ & \quad + \frac{{h_{c} }}{2}(A_{b26} - A_{t26} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(46)
$$ \begin{aligned} {\mathbf{K}}_{rf} & = \frac{{h_{c} }}{2}(A_{b66} - A_{t66} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ &\quad + \frac{{h_{c} }}{2}(A_{b26} - A_{t26} )\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial y} + \frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}(A_{b22} - A_{t22} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(47)
$$ \begin{aligned} {\mathbf{K}}_{rq} & = \left[ {\frac{{h_{c} (A_{t16} - A_{b16} )}}{2} - B_{b16} - B_{t16} } \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {\frac{{h_{c} (A_{t22} - A_{b22} )}}{2} - B_{b22} - B_{t22} } \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {\frac{{h_{c} (A_{t26} - A_{b26} )}}{2} - B_{b26} - B_{t26} } \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {\frac{{h_{c} (A_{t12} - A_{b12} )}}{2} - B_{b12} - B_{t12} } \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + [h_{c} (A_{t26} - A_{b26} ) - 2(B_{b26} + B_{t26} )] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + [h_{c} (A_{t66} - A_{b66} ) - 2(B_{b66} + B_{t66} )] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\mathbf{\varsigma }}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(48)
$$ \begin{aligned} {\mathbf{K}}_{gg} & = h_{c} Q_{c55} \int_{0}^{a} {\int_{0}^{b} {{\varvec{\upchi \upchi }}^{\text{T}} {\text{d}}x{\text{d}}y} }\\ & \quad + \frac{{h_{c}^{2} }}{4}\left( {A_{b11} + A_{t11} + \frac{{h_{c} Q_{c11} }}{3}} \right)\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c}^{2} }}{4}(A_{b16} + A_{t16} )\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial y} + \frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c}^{2} }}{4}\left( {A_{b66} + A_{t66} + \frac{{h_{c} Q_{c66} }}{3}} \right)\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial {\varvec{\upchi}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(49)
$$ \begin{aligned} {\mathbf{K}}_{gf} & = \frac{{h_{c}^{2} }}{4}(A_{b16} + A_{t16} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} }\\ & \quad + \frac{{h_{c}^{2} }}{4}\left( {A_{b12} + A_{t12} + \frac{{h_{c} Q_{c12} }}{3}} \right)\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c}^{2} }}{4}(A_{b26} + A_{t26} )\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} }\\ & \quad + \frac{{h_{c}^{2} }}{4}\left( {A_{b66} + A_{t66} + \frac{{h_{c} Q_{c66} }}{3}} \right)\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(50)
$$ \begin{aligned} {\mathbf{K}}_{gq} & = - h_{c} Q_{c55} \int_{0}^{a} {\int_{0}^{b} {{\varvec{\upchi}}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t11} - B_{b11} - \frac{{h_{c} (A_{t11} + A_{b11} )}}{2}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + h_{c} \left[ {B_{t16} - B_{b16} - \frac{{h_{c} (A_{t16} + A_{b16} )}}{2}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t12} - B_{b12} - \frac{{h_{c} (A_{t12} + A_{b12} )}}{2}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t16} - B_{b16} - \frac{{h_{c} (A_{t16} + A_{b16} )}}{2}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + h_{c} \left[ {B_{t66} - B_{b66} - \frac{{h_{c} (A_{t66} + A_{b66} )}}{2}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t26} - B_{b26} - \frac{{h_{c} (A_{t26} + A_{b26} )}}{2}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upchi}}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(51)
$$ \begin{aligned} {\mathbf{K}}_{ff} & = h_{c} Q_{c44} \int_{0}^{a} {\int_{0}^{b} {{\varvec{\upeta \upeta }}^{\text{T}} {\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c}^{2} }}{4}\left[ {A_{b66} + A_{t66} - \frac{{h_{c} Q_{c66} }}{3}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial x}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c}^{2} }}{4}(A_{b26} + A_{t26} )\int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial {\varvec{\upeta}}}}{\partial x}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial y} + \frac{{\partial {\varvec{\upeta}}}}{\partial y}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c}^{2} }}{4}\left( {A_{b22} + A_{t22} + \frac{{h_{c} Q_{c22} }}{3}} \right)\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial y}\frac{{\partial {\varvec{\upeta}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(52)
$$ \begin{aligned} {\mathbf{K}}_{fq} & = - h_{c} Q_{c44} \int_{0}^{a} {\int_{0}^{b} {{\varvec{\upeta}}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t16} - B_{b16} - \frac{{h_{c} (A_{t16} + A_{b16} )}}{2}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + h_{c} \left[ {B_{t66} - B_{b66} - \frac{{h_{c} (A_{t66} + A_{b66} )}}{2}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t26} - B_{b26} - \frac{{h_{c} (A_{t26} + A_{b26} )}}{2}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial x}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t12} - B_{b12} - \frac{{h_{c} (A_{t12} + A_{b12} )}}{2}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + h_{c} \left[ {B_{t26} - B_{b26} - \frac{{h_{c} (A_{t26} + A_{b26} )}}{2}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \frac{{h_{c} }}{2}\left[ {B_{t22} - B_{b22} - \frac{{h_{c} (A_{t22} + A_{b22} )}}{2}} \right]\int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upeta}}}}{\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(53)
$$ \begin{aligned} {\mathbf{K}}_{qq} & = h_{c} Q_{c55} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upzeta}}}}{\partial x}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad + h_{c} Q_{c44} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upzeta}}}}{\partial y}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {D_{t11} + D_{b11} + h_{c} (B_{b11} - B_{t11} ) + \frac{{h_{c}^{2} (A_{t11} + A_{b11} )}}{4}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{2} {\varvec{\upzeta}}}}{{\partial x^{2} }}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {D_{t22} + D_{b22} + h_{c} (B_{b22} - B_{t22} ) + \frac{{h_{c}^{2} (A_{t22} + A_{b22} )}}{4}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{2} {\varvec{\upzeta}}}}{{\partial y^{2} }}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + \left[ {D_{t12} + D_{b12} + h_{c} (B_{b12} - B_{t12} ) + \frac{{h_{c}^{2} (A_{t12} + A_{b12} )}}{4}} \right]\\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{2} {\varvec{\upzeta}}}}{{\partial x^{2} }}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }}{\text{d}}x{\text{d}}y} } \\ & \quad + 4\left[ {D_{t66} + D_{b66} + h_{c} (B_{b66} - B_{t66} ) + \frac{{h_{c}^{2} (A_{t66} + A_{b66} )}}{4}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{2} {\varvec{\upzeta}}}}{\partial x\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad + 2\left[ {D_{t16} + D_{b16} + h_{c} (B_{b16} - B_{t16} ) + \frac{{h_{c}^{2} (A_{t16} + A_{b16})}}{4}} \right] \\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial^{2} {\varvec{\upzeta}}}}{{\partial x^{2} }}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y} + \frac{{\partial^{2} {\varvec{\upzeta}}}}{\partial x\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial x^{2} }}} \right){\text{d}}x{\text{d}}y} } \\ & \quad + 2\left[ {D_{t26} + D_{b26} + h_{c} (B_{b26} - B_{t26} ) + \frac{{h_{c}^{2} (A_{t26} + A_{b26} )}}{4}} \right]\\ & \quad \times \int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial^{2} {\varvec{\upzeta}}}}{\partial x\partial y}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{{\partial y^{2} }} + \frac{{\partial^{2} {\varvec{\upzeta}}}}{{\partial y^{2} }}\frac{{\partial^{2} {\varvec{\upzeta}}^{\text{T}} }}{\partial x\partial y}} \right){\text{d}}x{\text{d}}y} } , \\ \end{aligned} $$
(54)
$$ \begin{aligned} {\mathbf{K}}_{rp} = {\mathbf{K}}_{pr}^{\text{T}} ,\quad {\mathbf{K}}_{gp} = {\mathbf{K}}_{pg}^{\text{T}} ,\quad {\mathbf{K}}_{fp} = {\mathbf{K}}_{pf}^{\text{T}} ,\quad {\mathbf{K}}_{qp} = {\mathbf{K}}_{pq}^{\text{T}} ,\quad {\mathbf{K}}_{gr} = {\mathbf{K}}_{rg}^{\text{T}} \hfill \\ {\mathbf{K}}_{fr} = {\mathbf{K}}_{rf}^{\text{T}} ,\quad {\mathbf{K}}_{qr} = {\mathbf{K}}_{rq}^{\text{T}} ,\quad {\mathbf{K}}_{fg} = {\mathbf{K}}_{gf}^{\text{T}} ,\quad {\mathbf{K}}_{qg} = {\mathbf{K}}_{gq}^{\text{T}} ,\quad {\mathbf{K}}_{qf} = {\mathbf{K}}_{fq}^{\text{T}} , \hfill \\ \end{aligned} $$
(55)
$$ {\mathbf{K}}_{\Delta T} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\mathbf{K}}_{\Delta T}^{qq} } \\ \end{array} } \right], $$
(56)
where
$$ \begin{aligned} {\mathbf{K}}_{\Delta T}^{qq} & = - F_{Tx} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upzeta}}}}{\partial x}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}{\text{d}}x{\text{d}}y} } \\ & \quad- F_{Tx} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial {\varvec{\upzeta}}}}{\partial y}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial y}{\text{d}}x{\text{d}}y} } \\ & \quad - F_{Txy} \int_{0}^{a} {\int_{0}^{b} {\left( {\frac{{\partial {\varvec{\upzeta}}}}{\partial x}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial y} + \frac{{\partial {\varvec{\upzeta}}}}{\partial y}\frac{{\partial {\varvec{\upzeta}}^{\text{T}} }}{\partial x}} \right){\text{d}}x{\text{d}}y} } . \\ \end{aligned} $$
(57)