Skip to main content
SpringerLink
Log in

Magneto-thermoelastic plane wave at the interface of pre-stressed water-aluminum-epoxy composite using Green and Lindsay’s model

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

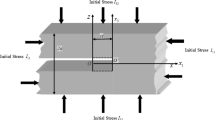
The reflection and refraction of magneto-thermoelastic plane wave at the interface of water-aluminum-epoxy composite in Green and Lindsay’s theory under initial stress has been investigated. Numerical computations are performed for the developed amplitude ratios of P-, SV- and thermal magneto-thermoelastic waves. For the values of relevant physical constants of water-aluminum-epoxy composite, the system of developed equations is solved by the application of the MATLAB software at different angles of incidence and the numerical computations are put graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

λ, μ :

Lame’s constants

ρ :

Density

σ :

Poisson’s ratio

c v :

Specific heat at constant strain

s ij :

Components of stress tensor

T:

Absolute temperature

T0 :

Reference temperature chosen so that |T − T0/T0| ≪ 1

P :

Initial pressure (s yy  − s xx )

e ij :

Components of strain tensor

K:

Thermal conductivity

J:

Current density vector

μ e :

1/[2(1 + σ)] magnetic permeability

ɛ e :

Electric permittivity

H:

Initial uniform magnetic intensity vector

h:

Induced magnetic field

H0 :

Magnetic field component

E:

Induced electric field vector

D:

Electric displacement vector

B:

Magnetic displacement vector

F :

Lorentz force

δ ij :

Kronecker delta

τ T :

Thermoelastic coupling constant

u i :

Components of displacement vector

τ 0, τ :

Relaxation times

t :

Time

e :

Cubical dilatation

Ω :

1/2( ∂v/∂x − ∂u/∂y)rotational component

α t :

Coefficient of linear thermal expansion

γ:

3λ + 2μ)α t

k :

Wave number

ω :

Angular frequency

c :

ω/k

c 21 :

(λ + 2μ +μ e H 20  + P)/ρ

c 22 :

μ − P/2)/ρ

c 23 :

K/ρc v

c 2 :

1/μ e ɛ e Light speed squared

References

  1. Cagniard L (1952) Comp Rend 234:1706–1713

    Google Scholar 

  2. Kaliski S (1965) Wave equations of thermo-electro-magnetoelasticity. Proc Vib Probl Pol Acad Sci 6(3):231–265

    MATH  MathSciNet  Google Scholar 

  3. Lord HW, Shulman Y (1967) A generalized dynamical theory of thermoelasticity. J Mech Phys Solids 15:299–309

    Article  MATH  ADS  Google Scholar 

  4. Green AE, Lindsay KA (1973) Thermoelasticity. J Elast 2:1–7

    Article  Google Scholar 

  5. Green AE, Naghdi PM (1991) A re-examination of the basic postulates of thermo-mechanics. Proc R Soc Lond A 432:171–194

    Article  MATH  MathSciNet  ADS  Google Scholar 

  6. Green AE, Naghdi PM (1992) On undamped heat waves in an elastic solid. J Therm Stresses 15:253–264

    Article  MathSciNet  ADS  Google Scholar 

  7. Green AE, Naghdi PM (1993) Thermoelasticity without energy dissipation. J Elast 31:189–208

    Article  MATH  MathSciNet  Google Scholar 

  8. Deresiewicz H (1960) Effect of boundaries on waves in thermoelastic solids: reflection of plane waves from a plane stress free boundary. J Mech Phys Solids 8:164–185

    Article  MATH  MathSciNet  ADS  Google Scholar 

  9. Gutenberg B (1944) Relation of reflected and refracted seismic waves. Bull Seismol Soc Am 34:85–102

    Google Scholar 

  10. Dey S, Addy SK (1977) Reflection of plane waves under initial stresses at a free surface. Int J Non Linear Mech 12:372–381

    Article  Google Scholar 

  11. Sinha SB, Elsibai KA (1997) Reflection and refraction of thermoelastic waves at an inter-face of two semi-infinite media with two relaxation times. J Therm Stresses 20:129–145

    Article  MathSciNet  Google Scholar 

  12. Jeffreys H (1930) The thermodynamics of elastic solids. Proc Cambridge Philos Soc 26:101–106

    Article  MATH  ADS  Google Scholar 

  13. Knott CG (1899) Reflection and refraction of elastic waves with seismological applications. Philos Mag 48:64–97

    Article  MATH  Google Scholar 

  14. Othman MIA, Song Y (2008) Reflection of magneto-thermoelastic waves with two relaxation times and temperature dependent elastic moduli. Appl Math Model 32:483–500

    Article  MATH  MathSciNet  Google Scholar 

  15. Daehnke A, Rossmanith HP (2009) Reflection and refraction of plane stress waves at interfaces modelling various rock joints. Geomech Geoeng 1(2):111–231

    Google Scholar 

  16. Chakraborty N, Singh MC (2011) Reflection and refraction of a plane thermoelastic wave at a solid–solid interface under perfect boundary condition, in presence of normal initial stress. Appl Math Model 35(11):5286–5301

    Article  MATH  MathSciNet  Google Scholar 

  17. Singh MC, Chakraborty N (2013) Reflection and refraction of P-, SV- and thermal wave, at an initially stressed solid–liquid interface in generalized thermoelasticity. Appl Math Model 37:463–475

    Article  MathSciNet  Google Scholar 

  18. Kaur R, Sharma JN (2012) Study of reflection and transmission of thermoelastic plane waves at liquid- solid interface. J Int Acad Phys Sci 16(2):109–116

    Google Scholar 

  19. Kumar R, Garg SK, Ahuja S (2013) Propagation of plane waves at the interface of an elastic solid half-space and a microstretch thermoelastic diffusion solid half-space. Latin Am J Solids Struct 10(6):1081–1108

    Article  Google Scholar 

  20. Sharma K, Bhargava RR (2014) Propagation of thermoelastic plane waves at an imperfect boundary of thermal conducting viscous liquid/generalized thermoelastic solid. Afrika Matematika 25(1):81–102

    Article  MATH  MathSciNet  Google Scholar 

  21. Lotfy K (2011) Transient disturbance in a half-space under generalized magneto-thermoelasticity with a stable internal heat source under three theories. Multidiscip Model Mater Struct 7(1):73–90

    Article  Google Scholar 

  22. Biot MA (1965) Mechanics of incremental deformations. Wiley, New York

    Google Scholar 

Download references

Acknowledgments

The authors are thankful to unknown reviewers for their valuable comments. This research has not received any specific grant from funding agency in the public, commercial, or not-for-profit sectors.

Conflict of interest

None declared.

Author information

Authors and Affiliations

  1. Department of Physics, GNA University, Hargobindgarh, Phagwara, Chotti Baradari, 163/1, Jalandhar, 144022, India

    Rajneesh Kakar

  2. Department of Electronics, SBBS University, Padhiana, Chotti Baradari, 163/1, Jalandhar, 144022, India

    Shikha Kakar

Authors
  1. Rajneesh Kakar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shikha Kakar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajneesh Kakar.

Appendix

Appendix

$$ c_{1}^{2} = \frac{{(\lambda + 2\mu + \mu_{e} {\rm H}_{0}^{2} + P)}}{\rho } = \frac{2\mu }{\rho }\left( {1 + a + \frac{\lambda }{2\mu } + \frac{{\mu_{e} {\rm H}_{0}^{2} }}{2\mu }} \right) $$
$$ c_{1}^{{{\prime }2}} = \frac{{(\lambda^{{\prime }} + \mu_{e}^{{\prime }} H_{0}^{{{\prime }2}} )}}{{\rho^{{\prime }} }} $$
$$ c_{2}^{2} = \frac{{\left( {\mu - \frac{P}{2}} \right)}}{\rho } = \frac{{\mu \left( {1 - a} \right)}}{\rho } $$
$$ \beta = \frac{P}{{\rho c_{2}^{2} }} = \frac{2a}{1 - a} $$
$$ c_{3}^{2} = \frac{\rm K}{{\rho c_{v} }} $$
$$ c_{3}^{{{\prime }2}} = \frac{{{\rm K}^{{\prime }} }}{{\rho^{{\prime }} c_{v}^{{\prime }} }} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kakar, R., Kakar, S. Magneto-thermoelastic plane wave at the interface of pre-stressed water-aluminum-epoxy composite using Green and Lindsay’s model. Meccanica 50, 3087–3102 (2015). https://doi.org/10.1007/s11012-015-0189-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-015-0189-x

Keywords

Search

Navigation