Photo-disintegration of the iron nucleus in fractured magnetite rocks with magnetostriction

Abstract

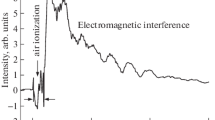
There has been considerable interest in recent experiments on iron nuclear disintegrations observed when rocks containing such nuclei are crushed and fractured. The resulting nuclear transmutations are particularly strong for the case of magnetite rocks, i.e. loadstones. We argue that the fission of the iron nucleus is a consequence of photo-disintegration. The electro-strong coupling between electromagnetic fields and nuclear giant dipole resonances are central for producing observed nuclear reactions. The large electron energies produced during the fracture of piezomagnetic rocks are closely analogous to the previously discussed case of the fracture of piezoelectric rocks. In both cases electro-weak interactions can produce neutrons and neutrinos from energetic protons and electrons thus inducing nuclear transmutations. The electro-strong condensed matter coupling discussed herein represents new many body collective nuclear photo-disintegration effects.

Appendix: Weak interactions

In years past we have been working on electro-weak interaction inverse beta decay [29–31] including electromagnetic interactions with collective plasma modes of motion. We have applied this theory to electron capture in a water plasma to explain observed nuclear transmutations on the cathode of a chemical cell [32].

1.1 Electron capture

Employing the electro-weak interaction wherein a heavy electron is captured by a nucleus to produce an added neutron and a neutrino, the electron capture rate for fully ionized plasmas can be computed if physical kinetic theory is employed in the following manner. (i) Consider the following reactions

$$(\hbox{general}) \quad e^{-} + \ ^A_ZX \rightarrow \ ^A_{(Z-1)}X +{\nu_e} \quad ({\hbox{special case}}) \quad {{\tilde{e}}^-}+{p^{+}} \rightarrow n+{\nu_{e}}, $$

(66)

wherein $\tilde{e}^-$ is an electron dressed by an external electromagnetic field. (ii) In the vacuum, the scattering amplitude for small relative velocity $v$ between the electron and the target is described by a complex scattering length

$$\begin{aligned} \mathcal{F}=a+ib, \end{aligned}$$

(67)

yielding an elastic and a total cross section given respectively by

$$\begin{aligned} \sigma _{el}=4\pi (a^2+b^2) \quad \sigma _{tot}=\frac{4\pi {\mathfrak {I}m \mathcal{F}}}{k}=\frac{4\pi \hbar b}{\mu v} \end{aligned}$$

(68)

wherein $\mu =mM/(m+M)$ is the reduced mass of the electron. (iii) The electron capture rate per scattering center in a two component neutral plasma is then

$$\begin{aligned} \Gamma =\left( \lim _{v\rightarrow 0} v\sigma _{tot}\right) \bar{n} =\left( \frac{4\pi \hbar b}{\mu }\right) \bar{n} . \end{aligned}$$

(69)

(iv) The density of electrons with positions $\{\bf{r}_j\}$ sitting right on top of a given nucleus at position $\{\bf{R}\}$ is described by an equilibrium correlation function,

$$\begin{aligned} \bar{n}=\left\langle \sum _j \delta ( \bf{R}-\bf{r}_j ) \right\rangle . \end{aligned}$$

(70)

Within the context of kinetic theory, which was not quite the many body quantum field theoretical approach taken in the original work [29], the central results are here given by Eqs. (69) and (70). It is the evaluation of Eq. (70) which has caused some controversy between us and with other workers at the University of Rome.

1.2 Electron correlation density $\bar{n}$

The computation of $\bar{n}$ made by the Rome University group [33] employed the zero temperature Hydrogen atomic bound state wave function at the origin

$$\begin{aligned} \bar{n}=\left| \psi _{bound}(0) \right| ^2=\frac{1}{\pi a_B^3}\ , \end{aligned}$$

(71)

wherein $a_B$ is the Bohr radius. Employing Eq. (5.3), Maiani et al. [33] calculated a rate smaller than that of our previous theory [29] by two orders of magnitude. We advised [34] the Rome group to calculate the correlation function in Eq. (70) employing a statistical ensemble at temperatureT ~ 5,000 K as in our previous theoretical work [29] but the Rome group took no notice of our reply to their calculation. We then pointed out more strongly that computing the rate using the ground state of Hydrogen was absurd because in the experiment the water plasma was so hot that it lighted up the laboratory. If the erroneous ground state computation of the Maiani et al. Eq. (71) held true, then the optical radiation would be virtually zero rather than blindingly bright. We further went on to show the Rome group how they should have approximately computed $\bar{n}$ for finite temperature. We employed Coulomb scattering state wave functions [35] for the fully ionized hot experimental [31] plasma. We found a substantially enhanced neutron production rate. The scattering wave function should replace the bound state wave function for estimates of the enhanced neutron production rate on water plasma drenched cathodes of chemical cells. Our purpose was to point out the source of this difference so that the physical principles may be resolved. Let us here present that calculation.

One must—for the physical plasma—employ the equation for $\bar{n}$ the hot temperature fully ionized dilute neutral plasma result for protons and electrons

$$\begin{aligned} \bar{n}_T=n\left\langle |\psi_{\bf{k}}(0)|^2\right\rangle, \end{aligned}$$

(72)

wherein $T$ is the temperature, $n$ is the number of electrons per unit volume averaged over the entire volume, $\psi_{\bf{k}}({\bf{r}})$ is the Coulomb scattering wave function normalized to a non-scattering plane wave $\psi^{0}_{\bf{k}}({\bf{r}})=\exp (i{\bf{k\cdot r}})$ and the thermal average is with respect to the Maxwell velocity distribution

$$\begin{aligned} \exp \left( -\frac{\hbar ^2 k^2}{2\mu k_BT}\right) = \exp \left( -\frac{\mu v^2}{2k_BT}\right) . \end{aligned}$$

(73)

The standard mathematical expression [36] for the scattering of an electron off a proton is given by

$$ \psi_{\bf{k}} ({\bf{r}})= e^{i\bf{k\cdot r}}\left[e^{\pi /2ka_B} \Gamma \left( 1-\frac{i}{ka_B}\right) \times _1F_1\left( \frac{i}{ka_B};1;\frac{kr-\bf{k\cdot r}}{ka_B}\right) \right]. $$

(74)

wherein $\Gamma (z)$ is the Gamma function and $_1F_1(\xi ;\zeta ;z)$ the confluent hypergeometric function. If $r\rightarrow 0$, then

$$ |\psi_{\bf{k}} (0)|^2=\frac{(2\pi e^2/\hbar v)}{1-exp(-(2\pi e^2/\hbar v))}\ . $$

(75)

The non-relativistic average, employing Eqs. (72), (73) and (75), has been computed -as by Bahcall [37]: $(v\ll c)$; i.e.

$$ \bar{n}_T=\frac{2\pi e^2 n}{\hbar }\left\langle\frac{1}{v}\right\rangle =n\left( \frac{e^2}{\hbar }\right) \sqrt{\frac{2\mu }{\pi k_BT}}\ . $$

(76)

Our final result for the kinetic model of a dilute neutral plasma consisting of electron and protons is the following:

$$ \Gamma _{T}= \left( \frac{4\pi \hbar b}{\mu }\right) \bar{n}_T, b\approx \frac{1}{8\pi ^2}\left( \frac{\hbar }{\mu c}\right) \left( \frac{G_F\mu ^2}{\hbar c}\right) ^2 \times \left(g_V^2+3g_A^2\right) \left(\gamma ^2-\gamma ^2_{threshold}\right), $$

(77)

wherein $G_F$ is the Fermi weak interaction coupling strength, $g_V$ and $g_A$ are respectively the vector and axial vector coupling strengths and

$$ \gamma = \left(\frac{m}{m_e}\right) ;\quad\gamma _{threshold} \sim 2.8 $$

(78)

We note in passing that the rate proportional to the inverse velocity occurs both theoretically and experimentally [38] also in the radiative corrections to $p\bar{p}$ annihilation near threshold.

At a physical temperature T ~ 5000 K, we recover our original $\Gamma$ value [29] two orders of magnitude higher for the kinetic model electron capture than that which was incorrectly computed by the Rome group.

1.3 Erroneous Maiani screening lengths

Most recently, the Rome group objected to our kinetic calculation on the grounds that we did not include Debye screening lengths into the fully ionized plasma kinetic calculation. An attempt to include Debye was carried out by Maiani et al. [39] who incorrectly found that the Coulomb potential is screened to within less than an Angstrom. This estimate is not sound, since it is very well known [40, 41] that the regime of validity demands that the Debye screening length is valid only if the thermal kinetic energy far exceeds the Coulomb potential energy; i.e.

$$\begin{aligned} k_BT \gg \frac{e^2}{L} > \frac{e^2}{\Lambda _D }, \end{aligned}$$

(79)

wherein $L$ is the mean spacing between charged particles and $\Lambda _D$ is the Debye screening length. At a temperature of $T\sim 5000\ ^oK$, Maiani et al. estimate $\Lambda _D \sim 10^{-8}\ \hbox{cm}$ which clearly violates the required Eq. (79) by a very large margin. The physical reason why the Rome group estimate for the Debye screening length is incorrect can be stated as follows: For the effective potential between two charges to be screened one must put many other charges between the original two charges. With a screening length on the scale of Angstroms such packing of additional charges is not possible for an electrolytic cell. The remainder of this Appendix is devoted to explaining in more detail, the screened Coulomb potential.

1.3.1 General theory of coulomb screening

If in an overall charge neutral isotropic system there are weak statistical fluctuations in the charge density $\rho (\bf{r})$, then due to photon exchange there will be a fluctuation energy

$$\begin{aligned} U[\rho ]=\frac{1}{2}\int \int \rho (\bf{r})\rho (\bf{r}^\prime ) V\big (|\bf{r}-\bf{r}^\prime |\big )\rm{d}^3 \bf{r}\rm{d}^3 \bf{r}^\prime , \end{aligned}$$

(80)

whence there will be a potential between charges given by

$$\begin{aligned} V(r)&= 4\pi \int \frac{e^{i\bf{k\cdot r}}}{k^2\varepsilon (k)} \left[ \frac{d^3\bf{k}}{(2\pi )^3}\right] \\ V(r)&= \frac{2}{\pi }\int \left[ \frac{\sin (kr)}{kr}\right] \ \frac{dk}{\varepsilon (k)}, \end{aligned}$$

(81)

wherein $\varepsilon (k)$ is the wave number dependent dielectric response function. For the vacuum, the dielectric response function is unity leading to the Coulomb potential $V_{\hbox{Coulomb}}(r) = 1/r$. For the general condensed matter situation, there will exist a screening function $S(r)$ which modifies the Coulomb potential to

$$\begin{aligned} V(r)&= \frac{1}{r} S(r), \\ S(r)&= \frac{2}{\pi } \int\limits_0^\infty \sin (kr) \left[ \frac{dk}{k \varepsilon (k)}\right] . \end{aligned}$$

(82)

The wave number dependent dielectric response function may also be found from the screening function via

$$\begin{aligned} \frac{1}{k\varepsilon (k)}= \int\limits_0^\infty \sin (kr)S(r)dr. \end{aligned}$$

(83)

The general Coulomb screening length

$$\begin{aligned} \Lambda =\frac{1}{\kappa } \quad ({\hbox{screening\ length}}) \end{aligned}$$

(84)

can be defined by either of two limits

$$\begin{aligned} \varepsilon (k)&= 1+\frac{\kappa ^2}{k^2}\ \ \ {\hbox{as}} \ \ \ k\rightarrow 0, \\ S(r)&= e^{-\kappa r} \quad {\hbox{as}} \quad r\rightarrow \infty . \end{aligned}$$

(85)

Equivalently rigorous formulas for the screening length are

$$\lim _{k\rightarrow 0} k^2\varepsilon (k)=\kappa ^2, \int V(r)d^3{\bf{r}}=\frac{4\pi }{\kappa ^2} =4\pi \int\limits_0^\infty r^2 V(r)dr. $$

(86)

The above rigorous results allow for the thermodynamic evaluation of the screening length $\Lambda =\kappa ^{-1}$.

1.3.2 Thermodynamic expression for $\kappa$

For an uncharged object in the thermodynamic limit of large volumes, the pressure function $P(T,\mu _1, \cdots \mu _f)$ of temperature and chemical potentials represents a complete thermodynamic description via

$$\begin{aligned} dP=sdT+\sum _{a=1}^f n_a d\mu _a \end{aligned}$$

(87)

wherein $s$ represents the entropy per unit volume and $n_a$ represents the number per unit volume of the $a^{th}$ chemical species with charge $z_a e$. For a mobile electron within the condensed matter system we choose $z_{\hbox{electron}}=-1$ as the charge convention. For a large sub-volume $V$ of the condensed matter system, the grand canonical ensemble number fluctuation theorem reads

$$\begin{aligned} \overline{\Delta N_a \Delta N_b} =V k_BT \left( \frac{\partial ^2 P}{\partial \mu _a \partial \mu _b}\right) _T. \end{aligned}$$

(88)

Since the object is charge neutral we have on average

$$\begin{aligned} \overline{Q}=e\sum _{a=1}^f z_a \overline{N_a} =0. \end{aligned}$$

(89)

However the charge does fluctuate according to

$$\begin{aligned} \overline{Q^2}=e^2\sum _{a=1}^f \sum _{b=1}^f z_a z_b \overline{\Delta N_a\Delta N_b}. \end{aligned}$$

(90)

In virtue of Eqs. (88) and (90) one has the charge fluctuation result

$$\begin{aligned} \overline{Q^2}=k_BTV e^2\sum _{a,b} z_a z_b \left( \frac{\partial ^2 P}{\partial \mu _a \partial \mu _b}\right) _T. \end{aligned}$$

(91)

On the other hand, for a uniform charging of the volume $V$ requires an energy computed from Eq,(80) employing $\rho =(Q/V)$

$$\begin{aligned} U_Q=\frac{1}{2}\left( \frac{Q^2}{V}\right) \left(\frac{4\pi }{\kappa ^2}\right)=\frac{Q^2}{2C_s}\ , \end{aligned}$$

(92)

wherein $C_s$ is the self capacitance of the volume; i.e.

$$\begin{aligned} C_s= \frac{V \kappa ^2}{4\pi } \end{aligned}$$

(93)

and Eq. (86) has been invoked. The Boltzmann factor $\exp (-U_Q/k_BT)$ yields a Gaussian distribution of charge values with dispersion

$$\begin{aligned} \overline{Q^2}=k_B T C_s=\frac{k_B TV\kappa ^2 }{4\pi }. \end{aligned}$$

(94)

Comparing Eqs. (91) and (94), one finds the central result of this section:

Theorem

The inverse screening length is determined by the thermodynamic equation of state:

$$\begin{aligned} \kappa ^2=4\pi e^2 \sum _{a,b} z_a z_b \left( \frac{\partial ^2 P}{\partial \mu _a \partial \mu _b}\right) _T. \end{aligned}$$

(95)

Depending on the equation of state we have qualitatively different kinds of screening derived from our central theorem. If we take the pressure of degenerate electrons, then we have Thomas-Fermi screening lengths. If the charged particles are dilute and classical, then the screening is that of Debye–Huckel, i.e. for the charge species of particles that are dilute

$$\begin{aligned} \left( \frac{\partial ^2 P}{\partial \mu _a \partial \mu _b}\right) _T =\frac{\delta _{ab} n_a}{k_BT} \qquad ({\hbox{dilute\ and\ classical}}), \end{aligned}$$

(96)

leading to the Debye screening of interest here

$$\begin{aligned} \kappa ^2=\frac{4\pi e^2}{k_BT}\sum _a z_a^2n_a . \end{aligned}$$

(97)

The validity of the classical Eq. (97) requires the inequality $k_BT \gg e^2\kappa$. Hence, the graph presented in their paper is meaningless for most of the densities [$n \ge 10^{18}/cm^3$] considered there.

1.3.3 Summary

Screening does not appreciably change our previous conclusions on the rates of electron captures in fully ionized plasmas as they appear in physical water cathode surface layers. The Rome group is in disagreement with our results only because they employed the Debye screening length in an unphysical regime of very short screening lengths where the Debye theory does not apply. This is amplified in our discussion of Sect. 7.3.