Abstract
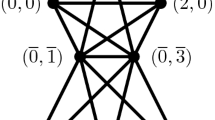
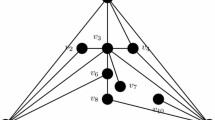
Let R be a commutative ring, let Z(R) be the set of all zero-divisors of R and Reg(R) = R\Z(R). The regular graph of R, denoted by G(R), is a graph with all elements of Reg(R) as the vertices, and two distinct vertices x, y ∈ Reg(R) are adjacent if and only if x+y ∈ Z(R). In this paper we show that if R is a commutative Noetherian ring and 2 ∈ Z(R), then the chromatic number and the clique number of G(R) are the same and they are 2n, where n is the minimum number of prime ideals whose union is Z(R). Also, we prove that all trees that can occur as the regular graph of a ring have at most two vertices.
Similar content being viewed by others
References
S. Akbari, D. Kiani, F. Mohammadi and S. Moradi, The total graph and regular graph of a commutative ring, J. Pure Appl. Algebra, 213 (2009), 2224–2228.
D. F. Anderson and A. Badawi, The total graph of a commutative ring, J. Algebra, 320 (2008), 2706–2719.
M. F. Atiyah and I. G. Macdonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Company, 1969.
J. A. Bondy and U. S. R. Murty, Graph Theory with Applications, Elsevier Publishing Company, New York, 1976.
J. A. Huckaba, Commutative Rings with Zero Divisors, Marcel Dekker, New York, 1988.
R. Y. Sharp, Steps in Commutative Algebra, Second Edition, Cambridge University Press, 2000.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by László Fuchs
Rights and permissions
About this article
Cite this article
Akbari, S., Heydari, F. The regular graph of a commutative ring. Period Math Hung 67, 211–220 (2013). https://doi.org/10.1007/s10998-013-7039-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10998-013-7039-1