Skip to main content
SpringerLink
Log in

Quantification in Some Non-normal Modal Logics

  • Published:
Journal of Philosophical Logic Aims and scope Submit manuscript

Abstract

This paper offers a semantic study in multi-relational semantics of quantified N-Monotonic modal logics with varying domains with and without the identity symbol. We identify conditions on frames to characterise Barcan and Ghilardi schemata and present some related completeness results. The characterisation of Barcan schemata in multi-relational frames with varying domains shows the independence of BF and CBF from well-known propositional modal schemata, an independence that does not hold with constant domains. This fact was firstly suggested for classical modal systems by Stolpe (Logic Journal of the IGPL 11(5), 557–575, 2003), but unfortunately that work used only models and not frames.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

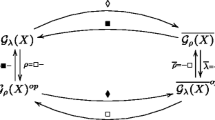
  1. In Section 3 the reader can find two tables and a figure classifying the main systems and schemata.

  2. For this reason, throughout the paper we will use interchangeably the expressions “Kripke frame/model”, “relational frame/model”, and “1-relational frame/model”.

  3. The strong version, on the other hand, is as follows [24]:@@@@

    Things here are the same as in Eq. 1, except that ϕ is required to be true in w ′ if and only if w ′ is related with w by any relation R j . The technical motivation of this second choice is that the resulting semantics is appropriate for any (non-normal) modal logics including the classical ones, i.e., the weakest ones that only consist of RE, ⊩A⇔B/⊩□A⇔□B. On the contrary, the version with Eq. 1 validates, among others, RM, i.e., ⊩A→B/⊩□A→□B, which opens the door to stronger logics below system K. However, multi-relational models based on the clause (2) make the semantics different from Kripke’s, despite the structural similarity of how worlds are connected in frames.

  4. When clear form the context, we also omit the reference to the model. The truth set of a closed formula does not depend on any interpretation and assignment.

  5. Indeed \(\phantom {\dot {i}\!}\phantom {\dot {i}\!}\vdash _{\textsf {Q}^{\circ }_{=} . \textsf {MN}} \bot \to \neg A\) ex falso quodlibet, \(\phantom {\dot {i}\!}\phantom {\dot {i}\!}\vdash _{\textsf {Q}^{\circ }_{=} . \textsf {MN}} \Box \bot \to \Box \neg A\) by RM, \(\phantom {\dot {i}\!}\phantom {\dot {i}\!}\vdash _{\textsf {Q}^{\circ }_{=} . \textsf {MN}} \Diamond A \to \Diamond \top \) by contraposition.

References

  1. Arló-Costa, H. (2002). First order extensions of classical systems of modal logic. Studia Logica, 71, 87–118.

    Article  Google Scholar 

  2. Arló-Costa, H. (2011). Quantified modal logic. In Gupta, A., & van Benthem, J. (Eds.) Logic and philosophy today, Vol. 2. London: College Publications.

  3. Arló-Costa, H. L., & Pacuit, E. (2006). First-order classical modal logic. Studia Logica, 84(2), 171–210.

    Article  Google Scholar 

  4. Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal logic: Cambridge University Press.

  5. Brauner, T., & Ghilardi, S. (2007). First-order modal logic. In Blackburn, P., van Benthem, J., & Wolter, F. (Eds.) Handbook of modal logic: Elsevier.

  6. Calardo, E., & Rotolo, A. (2014). Variants of multi-relational semantics for propositional non-normal modal logics. Journal of Applied Non-Classical Logics, 24 (4), 293–320.

    Article  Google Scholar 

  7. Chellas, B. (1980). Modal logic: an introduction: Cambridge University Press.

  8. Corsi, G. (2002). A unified completeness theorem for quantified modal logics. Journal of Symbolic Logic, 67(4), 1483–1510.

  9. Elgesem, D. (1997). The modal logic of agency. Nordic Journal of Philosophical Logic, 2, 1– 46.

    Google Scholar 

  10. Fagin, R., Halpern, J. Y., Moses, Y., & Vardi, M.Y. (1995). Reasoning about knowledge: MIT Press.

  11. Fitting, M., & Mendelsohn, R. L. (1998). First order modal logic. London: Kluwer Academic Publishers.

    Book  Google Scholar 

  12. Gabbay, D. (1976). Investigations in modal and tense logics with applications to problems in philosophy and linguistics. Reidel.

  13. Gabbay, D., Shehtman, V., & Skvortsov, D. (2009). Quantification in nonclassical logic. Number v. 1 in Studies in logic and the foundations of mathematics. Elsevier.

  14. Garson, J. (2001). Quantification in modal logic. In Gabbay, D., & Guenthner, F. (Eds.) Handbook of philosophical logic. 2nd edn.: Kluwer.

  15. Garson, J. (2005, October). Unifying quantified modal logic. Journal of Philosophical Logic, 34(5), 621–649.

  16. Gasquet, O., & Herzig, A. (1996). From classical to normal modal logic. In Wansing, H. (Ed.) Proof theory of modal logic (pp. 293–311). Dordrecht: Kluwer.

  17. Goble, L. (2001). Multiplex semantics for deontic logic. Nordic Journal of Philosophical Logic, 5(2), 113–134.

    Article  Google Scholar 

  18. Goble, L. (2003). Preference semantics for deontic logic part I–Simple models. Logique et Analyse, 46, 383–418.

    Google Scholar 

  19. Goble, L. (2004a). Preference semantics for deontic logic — Part II: Multiplex models. Logique et Analyse, 47, 113–134.

  20. Goble, L. (2004b). A proposal for dealing with deontic dilemmas. In Lomuscio, A., & Nute, D. (Eds.) Deontic logic, volume 3065 of lecture notes in computer science (pp. 74–113). Berlin - Heidelberg: Springer.

  21. Goble, L. (2005). A logic for deontic dilemmas. Journal of Applied Logic, 3 (3–4), 461–483.

    Article  Google Scholar 

  22. Goldblatt, R. (1992). Logics of time and computation (2. ed.). Number 7 in CSLI lecture notes Stanford. CA: Center for the Study of Language and Information.

    Google Scholar 

  23. Goldblatt, R. (2011). Quantifiers, propositions and identity: admissible semantics for quantified modal and substructural logics: Cambridge University Press.

  24. Governatori, G., & Rotolo, A. (2005). On the axiomatization of Elgesem’s logic of agency and ability. Journal of Philosophical Logic, 34(4), 403–431.

  25. Hansen, H. H. (2003). Monotonic modal logics. Master’s thesis, ILLC, Universiteit van Amsterdam, Amsterdam.

  26. Jennings, R. E., & Schotch, P. K. (1981a). Non-Kripkean Deontic logic. In Hilpinen, R. (Ed.) New studies in deontic logic: norms, actions, and the foundations of ethics (pp. 149–162). Dordrecht, Holland: D. Reidel Publishing Company.

  27. Jennings, R. E., & Schotch, P. K. (1981b). Some remarks on (weakly) weak modal logics. Notre Dame J. Formal Logic, 22(4), 309–314.

  28. Jones, A., & Carmo, J. (2002). Deontic logic and contrary-to-duties. In Gabbay, D., & Guenthner, F. (Eds.) Handbook of philosophical logic. 2nd edn. Dordrecht; Boston: Kluwer Academic Publishers.

  29. Kracht, M., & Wolter, F. (1999). Normal monomodal logics can simulate all others. Journal of Symbolic Logic, 64(1), 99–138.

    Article  Google Scholar 

  30. Kripke, S. (1963). Semantical considerations on modal logic. Acta Philosophica Fennica, 16, 83–94.

    Google Scholar 

  31. Kripke, S. (1980). Naming and necessity: Blackwell Publishers.

  32. Montague, R. (1970). Universal grammar. Theoria, 36(3), 373–98.

    Article  Google Scholar 

  33. Parikh, R. (1985). The logic of games and its applications. Annals of Discrete Mathematics, 24, 111–140.

    Google Scholar 

  34. Pauly, M. (2002). A modal logic for coalitional power in games. Journal of Logic and Computation, 12, 149–166.

    Article  Google Scholar 

  35. Scott, D. (1970). Advice in modal logic. In Hilpinen, R. (Ed.) Philosophical problems in logic (pp. 143–173). Dordrecht: Reidel.

  36. Segerberg, K. (1971). An Essay in Classical Modal Logic (Uppsala Universitet ed.) Vol. 13. Filosofiska Studier: Uppsala.

  37. Segerberg, K. (1992). Getting started: beginnings in the logic of action. Studia Logica, 51(3/4), 347–378.

    Article  Google Scholar 

  38. Stolpe, A. (2003). QMML: quantified minimal modal logic and its applications. Logic Journal of the IGPL, 11(5), 557–575.

    Article  Google Scholar 

  39. Waagbø, G. (1992). Quantified modal logic with neighborhood semantics. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 38, 491–499.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. CIRSFID - University of Bologna, Bologna, Italy

    Erica Calardo & Antonino Rotolo

Authors
  1. Erica Calardo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Antonino Rotolo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antonino Rotolo.

Additional information

Partially supported by the UNIBO project FARB 2012 Mortality Salience, Legal and Social Compliance, and Economic Behaviour: Theoretical Models and Experimental Methods and by the EU H2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 690974 for the project MIREL: MIning and REasoning with Legal texts.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Calardo, E., Rotolo, A. Quantification in Some Non-normal Modal Logics. J Philos Logic 46, 541–576 (2017). https://doi.org/10.1007/s10992-016-9410-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10992-016-9410-1

Keywords

Search

Navigation