Abstract
Quasi-Newton and truncated-Newton methods are popular methods in optimization and are traditionally seen as useful alternatives to the gradient and Newton methods. Throughout the literature, results are found that link quasi-Newton methods to certain first-order methods under various assumptions. We offer a simple proof to show that a range of quasi-Newton methods are first-order methods in the definition of Nesterov. Further, we define a class of generalized first-order methods and show that the truncated-Newton method is a generalized first-order method and that first-order methods and generalized first-order methods share the same worst-case convergence rates. Further, we extend the complexity analysis for smooth strongly convex problems to finite dimensions. An implication of these results is that in a worst-case scenario, the local superlinear or faster convergence rates of quasi-Newton and truncated-Newton methods cannot be effective unless the number of iterations exceeds half the size of the problem dimension.
Similar content being viewed by others
References
Conn, A.R., Gould, N.I.M., Toint, P.L.: Trust-Region Methods. SIAM, Philadelphia (2000)
Fletcher, R.: Practical Methods of Optimization, 2nd edn. Wiley, Hoboken (2000)
Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer Series in Operations Research, Berlin (2006)
Broyden, C.G.: Quasi-Newton methods and their application to function minimization. Math. Comput. 21, 368–381 (1967)
Huang, H.Y.: Unified approach to quadratically convergent algorithms for function minimization. J. Optim. Theory Appl. 5(6), 405–423 (1970)
Broyden, C.G.: The convergence of a class of double-rank minimization algorithms: 2. The new algorithm. IMA J. Appl. Math. 6(3), 222–231 (1970)
Fletcher, R.: A new approach to variable metric algorithms. Comput. J. 13(3), 317–322 (1970)
Goldfarb, D.: A family of variable-metric methods derived by variational means. Math. Comput. 24(109), 23–26 (1970)
Shanno, D.F.: Conditioning of quasi-Newton methods for function minimization. Math. Comput. 24(111), 647–656 (1970)
Davidon, W.C.: Variance algorithm for minimization. Comput. J. 10(4), 406–410 (1968)
Fiacco, A.V., McCormick, G.P.: Nonlinear Programming. Wiley, New York (1968)
Murtagh, B.A., Sargent, R.W.H.: A constrained minimization method with quadratic convergence. In: Optimization. Academic Press, London (1969)
Wolfe, P.: Another variable metric method. Working paper (1968)
Davidon, W.C.: Variable metric method for minimization. Technical report. AEC Research and Development Report, ANL-5990 (revised) (1959)
Fletcher, R., Powell, M.J.D.: A rapidly convergent descent method for minimization. Comput. J. 6(2), 163–168 (1963)
Hull, D.: On the huang class of variable metric methods. J. Optim. Theory Appl. 113(1), 1–4 (2002)
Nocedal, J.: Updating quasi-Newton matrices with limited storage. Math. Comput. 5, 773–782 (1980)
Liu, D.C., Nocedal, J.: On the limited-memory BFGS method for large scale optimization. Math. Program. 45, 503–528 (1989)
Meyer, G.E.: Properties of the conjugate gradient and Davidon methods. J. Optim. Theory Appl. 2(4), 209–219 (1968)
Polak, E.: Computational Method in Optimization. Academic Press, Cambridge (1971)
Ben-Tal, A., Nemirovski, A.: Lecture notes: optimization iii: Convex analysis, nonlinear programming theory, nonlinear programming algorithms. Georgia Institute of Technology, H. Milton Stewart School of Industrial and System Engineering. http://www2.isye.gatech.edu/~nemirovs/OPTIII_LectureNotes.pdf (2013)
Shanno, D.F.: Conjugate gradient methods with inexact searches. Math. Oper. Res. 3(3), 244–256 (1978)
Dixon, L.C.W.: Quasi-newton algorithms generate identical points. Math. Program. 2(1), 383–387 (1972)
Nocedal, J.: Finding the middle ground between first and second-order methods. OPTIMA 79— Mathematical Programming Society Newsletter, discussion column (2009)
Nemirovskii, A.S., Yudin, D.B.: Problem Complexity and Method Efficiency in Optimization. Wiley, New York (1983). First published in Russian (1979)
Nesterov, Y.: Introductory Lectures on Convex Optimization, A Basic Course. Kluwer Academic Publishers, Berlin (2004)
Nesterov, Y.: A method for unconstrained convex minimization problem with the rate of convergence \(O({1}/{k^2})\). Dokl. AN SSSR (translated as Soviet Math. Docl.) 269, 543–547 (1983)
Nesterov, Y.: On an approach to the construction of optimal methods of minimization of smooth convex functions. Ekonom. i. Mat. Mettody 24, 509–517 (1988)
Nesterov, Y.: Smooth minimization of nonsmooth functions. Math. Program. Ser. A 103, 127–152 (2005)
Nesterov, Y.: Gradient methods for minimizing composite objective function. Université Catholique de Louvain, Center for Operations Research and Econometrics (CORE). No 2007076, CORE discussion papers (2007)
Bioucas-Dias, J.M., Figueiredo, M.A.T.: A new TwIST: two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 16(12), 2992–3004 (2007)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2, 183–202 (2009)
Tseng, P.: On accelerated proximal gradient methods for convex-concave optimization. unpublished manuscript (2008)
Gregory, R.T., Karney, D.L.: A Collection of Matrices for Testing Computational Algorithms. Wiley, New York (1969)
Acknowledgments
The authors would like to thank the anonymous reviewers of an earlier submission of this manuscript. The first author thanks Lieven Vandenberghe for interesting discussions on the subject. The second author thanks Michel Baes and Mike Powell for an inspirational and controversial discussion on the merits of global iteration complexity versus locally fast convergence rates in October 2007 at OPTEC in Leuven. Grants The work of T. L. Jensen was supported by The Danish Council for Strategic Research under Grant No. 09-067056 and The Danish Council for Independent Research under Grant No. 4005-00122. The work of M. Diehl was supported by the EU via FP7-TEMPO (MCITN-607957), ERC HIGHWIND (259166), and H2020-ITN AWESCO (642682).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ilio Galligani.
Appendices
Appendix 1: Proof of Theorem 2.2
Proof
We will follow the approach [26, The. 2.1.13] but for finite-dimensional problems (this is more complicated as indicated in [26, p. 66]). Consider the problem instance
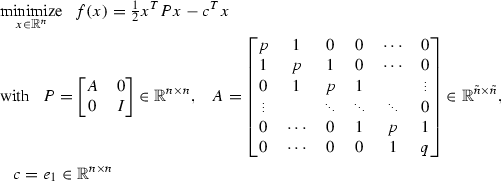
where \({\tilde{n}}\le n\) and the initialization \(x_0 = 0\). We could also have generated the problem \({\bar{f}}({\bar{x}}) = f({\bar{x}} + \bar{x}_0)\) and initialized it at \({\bar{x}}_0\) since this is just a shift of sequences of any first-order method. To see this, let \(k\ge 1\) and \({\bar{x}} \in {\bar{x}}_0 + {\bar{F}}_k\) be an allowed point for a first-order method applied to a problem with objective \({\bar{f}}\) using \({\bar{x}}_0\) as initialization. Let \(x = {\bar{x}} + {\bar{x}}_0\), then
Consequently \(x \in F_k = {\bar{F}}_k\) and we can simply assume \(x_0 = 0\) in the following.
We select \(p = 2+\mu \) and \(q=(p+\sqrt{p^2-4})/2\) with the bounds \(1\le q \le p\). Then:
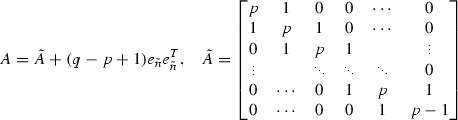
The value \(q-p+1\ge 0 \) for \(\mu \ge 0\). The eigenvalues of the matrix \({\tilde{A}}\) are given as [34]
The smallest and largest eigenvalues of A are then bounded as
With \(\mu \le 1\), we have \(\lambda _\mathrm{min}(P) = \lambda _\mathrm{min} (A)\) and \(\lambda _\mathrm{max}(P) = \lambda _\mathrm{max} (A)\). The condition number is given by \(Q=\frac{L}{\mu } = \frac{p+3}{p-2}=\frac{5+\mu }{\mu }\ge 6\), and the solution is given as \(x^\star = P^{-1} e_1\). The inverse \(A^{-1}\) can be found in [34], and the ith entry of the solution is then
where
Since q is a root of the second-order polynomial \(y^2-p y+1\), we have \(s_i = q^i,\forall i\ge 0\). Using \(Q = \frac{p+3}{p-2} \Leftrightarrow p = 2\frac{Q+\frac{3}{2}}{Q-1}\) and then
A simple calculation of \(\beta \) in (17) can for instance be \(\beta = \frac{\frac{3}{2} + \sqrt{{\textstyle \frac{1}{2}}+ 5 Q}}{\sqrt{Q}} \Big \vert _{Q=8} \simeq 2.78\), which is sufficient for any \(Q \ge 8\). However, solving the nonlinear equation yields that \(\beta =1.1\) is also sufficient for any \(Q \ge 8\). Since \(\nabla f(x) = P x - c\), the set \(F_k\) expands as:
Since P is tridiagonal and \(x_0 = 0\), we have
Considering the relative convergence
Fixing \({\tilde{n}}=2k\), we have for \(k = {\textstyle \frac{1}{2}}{\tilde{n}} \le {\textstyle \frac{1}{2}}n\)
and inserting (17) yields
\(\square \)
Remark We note that it is possible to explicitly state a smaller \(\beta \) and hence a tighter bound, but we prefer to keep the explanation of \(\beta \) simple.

Appendix 2: Proof of Corollary 3.3
For this proof, we note that the multiplication \({\bar{H}}_k \nabla f(x_k)\) can be calculated efficiently via Algorithm 1 [3, Alg. 7.4]. From Algorithm 1, we obtain that with \({\bar{H}}_k^0 = \gamma _k I\) and using (6),
and then recursively inserting
The iterations are then given as
and L-BFGS is a first-order method. \(\square \)
Rights and permissions
About this article
Cite this article
Jensen, T.L., Diehl, M. An Approach for Analyzing the Global Rate of Convergence of Quasi-Newton and Truncated-Newton Methods. J Optim Theory Appl 172, 206–221 (2017). https://doi.org/10.1007/s10957-016-1013-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-016-1013-z