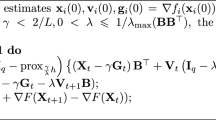Distributed Price Adjustment Based on Convex Analysis

Abstract

In this paper, we suggest a distributed process of price adjustment toward a partial market equilibrium. As the main contribution, our algorithm of price adjustment is computationally efficient and decentralized. Its convergence properties are crucially based on convex analysis. The proposed price adjustment corresponds to a subgradient scheme for minimizing a special nonsmooth convex function. This function is the total excessive revenue of the market’s participants and its minimizers are equilibrium prices. As the main result, the algorithm of price adjustment is shown to converge to equilibrium prices. Additionally, the market clears on average during the price adjustment process, i.e., by historical averages of supply and demand. Moreover, a global rate of convergence is obtained. We endow our algorithm with decentralized prices by introducing the trade design with price initiative of producers. The latter suggests that producers settle and update their individual prices, and consumers buy at the lowest purchase price.

Appendix

This Appendix is devoted to the proof of Lemma 4.1. For that, we first present the quasi-monotone subgradient method for nonsmooth convex minimization from [1]. As already mentioned, the price adjustment process (PA) can be seen as an implementation of this scheme. Here, in addition to [1], the quasi-monotone subgradient method is modified in order to incorporate varying step sizes for different goods. Using this fact, we prove Lemma 4.1 in the second part of “Appendix”.

1.1 Quasi-monotone Subgradient Method

Consider the following minimization problem:

$$\begin{aligned} \min _{x \in X} f(x), \end{aligned}$$

(32)

where $X \subset \mathbb {R}^n$ is a closed convex set with nonempty interior $\text{ int }\,X$, and f is a convex function on $\mathbb {R}^n$. Moreover, let f be representable as a maximum of concave functions, i.e.,

$$\begin{aligned} f(x) = \max _{a \in A} {\varPhi }(a) + \varphi (x,a), \end{aligned}$$

(33)

where $A \subset \mathbb {R}^m$ is a closed and convex set, $\varphi (\cdot ,a)$ is a convex function on $\mathbb {R}^n$ for every $a \in A$, and ${\varPhi }, \varphi (x,\cdot )$ are concave functions on $\mathbb {R}^m$ for every $x \in X$. Denote by a(x) one of the optimal solutions of the maximization problem in (33). Then, $\nabla f(x) := \nabla _x \varphi (x, a(x))$ is a subgradient of f at x. Recall that for an arbitrary subgradient $\nabla f(x)$ at $x \in X$ of a convex function f we have:

$$\begin{aligned} f(y) \ge f(x) + \langle \nabla f(x), y-x\rangle , \quad y \in X. \end{aligned}$$

(34)

Using the representation (33), we also have:

$$\begin{aligned} \min _{x \in X} f(x) = \min _{x \in X} \max _{a \in A} \left[ {\varPhi }(a) + \varphi (x,a) \right] = \max _{a \in A} \left[ {\varPhi }(a) + \min _{x \in X} \varphi (x,a)\right] . \end{aligned}$$

The latter maximization problem is called adjoint to (32) with the adjoint variable $a \in A$.

For the set X, we assume to be known a prox-function d(x).

Definition 5.1

$d\,{:}\,X \mapsto \mathbb {R}$ is called a prox-function for X if the following holds:

• $d(x) \ge 0$ for all $x \in X$ and $d(x[0]) = 0$ for certain $x[0] \in X$;

• d is strongly convex on X with convexity parameter one:

  $$\begin{aligned} d(y) \ge d(x) + \langle \nabla d(x), y-x \rangle + \frac{1}{2} \Vert y-x\Vert ^2, \quad x,y \in X, \end{aligned}$$

  (35)

  where $\Vert \cdot \Vert$ is a norm on $\mathbb {R}^n$.

• Auxiliary minimization problem

  $$\begin{aligned} \min _{x \in X} \left\{ \langle z, x\rangle + \chi d(x) \right\} \end{aligned}$$

  (36)

  is easily solvable for $z \in \mathbb {R}^n, \chi > 0$.

For a sequence of positive parameters $\left\{ \chi [t] \right\} _{t \ge 0}$, we consider the following iteration:

Next Theorem 5.1 is crucial for the convergence analysis of the quasi-monotone subgradient method (SM). It estimates the duality gap for the minimization problem (32) and its adjoint problem evaluated at the historical averages.

For that, we define the penalty term $h_t$ and the remainder term $\rho _t, t \ge 0$, as follows:

$$\begin{aligned} h_t(a):= & {} - \min _{x \in X} \left\{ \varphi (x,a) + \frac{\chi [t]}{t+1} d(x) \right\} , \quad \rho _t := \frac{1}{t+1} \sum _{r=0}^{t} \frac{1}{2 \chi [r-1]} \left\| \nabla f(x[r])\right\| _*^2. \end{aligned}$$

Here, $\Vert \cdot \Vert _*$ is the conjugate norm to $\Vert \cdot \Vert$, i.e.,

$$\begin{aligned} \Vert s\Vert _* := \max _{s \in \mathbb {R}^n} \left\{ \langle s, x \rangle \,{:}\,\Vert x\Vert \le 1 \right\} , \quad s \in \mathbb {R}^n. \end{aligned}$$

(37)

Further, we define the average adjoint state $a[t] := \frac{1}{t+1} \sum \nolimits _{r=0}^{t} a(x[r]), \quad t \ge 0.$ Note that $a[t] \in A$, since A is convex. Theorem 5.1 is motivated by the estimating sequence technique (e.g., Section 2.2.1 in [3]).

Theorem 5.1

[1] Let the sequence $\left\{ x[t] \right\} _{t \ge 0}$ be generated by (SM) with nondecreasing parameters

$$\begin{aligned} \chi [t+1] \ge \chi [t], \quad t \ge 0. \end{aligned}$$

(38)

Then, for all $t \ge 0$ we have

$$\begin{aligned} f(x[t]) - {\varPhi }(a[t]) + h_t(a[t]) \le \rho _t. \end{aligned}$$

(39)

Additionally, we need the following simple result on the quadratic penalty for the general convex optimization problems. From now on, let us consider the maximization problem

$$\begin{aligned} {\varPhi }^* := \max _{\begin{array}{c} a \in A \end{array}} \left\{ {\varPhi }(a)\,{:}\,g_l(a) \le 0, l=1,\ldots , L \right\} , \end{aligned}$$

(40)

where $A \subset \mathbb {R}^m$ is a closed convex set, ${\varPhi }$ is a concave function, and $g_l(\cdot ), l=1,\ldots , L$ are convex functions on $\mathbb {R}^m$. We assume that the convex feasible set of the maximization problem (40) has a Slater point (e.g., [19]).

Lemma 5.1

For any $\kappa > 0$, we have

$$\begin{aligned} \mathop {\max }\limits _{a \in A} \left[ {\varPhi }(a) - \frac{\kappa }{2} \sum _{l=1}^{L} \left( g_l(a)\right) _+^2 \right] \le {\varPhi }^* + \frac{1}{2 \kappa } \sum _{l=1}^{L} \lambda _l^*, \end{aligned}$$

where $\lambda _l^*, l=1, \ldots , L$ are Lagrange multipliers for an optimal solution of (40).

1.2 Proof of Lemma 4.1

We start by proving that the price adjustment process (PA) is a variant of the quasi-monotone subgradient method (SM). For that, it enough to show that

• (1) the price forecast (25) can be obtained using the Euclidean prox-function,

• (2) $\mathcal {E}$ can be represented as the maximum of a parametric family of concave functions.

Firstly, we define the Euclidean prox-functions:

$$\begin{aligned} d_k(p) := \frac{1}{2} \sum _{j=1}^{n} \frac{1}{\zeta _k^{(j)}} \left( p^{(j)}\right) ^2, \quad k=1, \ldots , K, \end{aligned}$$

where $\zeta _k^{(j)}$ are positive scaling coefficients. The corresponding norms in Definition 5.1 and their conjugates according to (37) are

$$\begin{aligned} \Vert p\Vert ^2_k = \sum _{j=1}^{n} \frac{1}{\zeta _k^{(j)}} \left( p^{(j)}\right) ^2,\quad \Vert s\Vert ^2_{k*} = \sum _{j=1}^{n} \zeta _k^{(j)} \left( s^{(j)}\right) ^2, \quad k=1, \ldots , K. \end{aligned}$$

For $z_k[t] \in \mathbb {R}^n, \chi _k[t] > 0$, consider the auxiliary minimization problem of Step 3 in (SM):

$$\begin{aligned} \min _{p_1, \ldots , p_K \in \mathbb {R}^n_+} \left\{ \sum _{k=1}^{K} \langle z_k[t], p_k\rangle + \chi _k[t] d_k(p_k) \right\} . \end{aligned}$$

(41)

Its unique solution is the price forecast (25) defined in Step 3 of (PA):

$$\begin{aligned} p_k^{+(j)}[t]= \frac{\zeta ^{(j)}_k}{\chi _k[t]}\left( -z_k^{(j)}[t] \right) _+, \quad j= 1, \ldots , n,\quad k=1, \ldots , K. \end{aligned}$$

Secondly, it follows from (21) in Lemma 3.2, that the total excessive revenue is representable as a maximum of concave functions:

$$\begin{aligned} \mathcal {E}(p_1, \ldots , p_K) = \max _{\left( \alpha , {\widetilde{y}}, \beta , {\widetilde{x}} \right) \in \mathcal {A}} {\varPhi }\left( \alpha , {\widetilde{y}}, \beta , {\widetilde{x}} \right) + \varphi \left( p_1, \ldots , p_K, {\widetilde{y}}, {\widetilde{x}} \right) , \end{aligned}$$

where

$$\begin{aligned} \varphi \left( p_1, \ldots , p_K, {\widetilde{y}}, {\widetilde{x}} \right) = \sum _{k=1}^{K} \left\langle p_k, {\widetilde{y}}_k \right\rangle - \left\langle \min _{k=1, \ldots , K} p_k, \sum _{i=1}^{I} {\widetilde{x}}_i \right\rangle . \end{aligned}$$

Overall, we can apply Theorem 5.1 in order to get the following inequality:

$$\begin{aligned} \mathcal {E}(p_1[t], \ldots , p_K[t]) - {\varPhi }\left( \alpha [t], {\widetilde{y}}[t], \beta [t], {\widetilde{x}}[t] \right) + h_t\left( {\widetilde{y}}[t], {\widetilde{x}}[t]\right) \le \rho _t, \end{aligned}$$

(42)

where

$$\begin{aligned}&h_t\left( {\widetilde{y}}[t], {\widetilde{x}}[t]\right) \\&\quad = - \min _{p_1, \ldots , p_K \in \mathbb {R}^n_+} \left\{ \varphi \left( p_1, \ldots , p_K, {\widetilde{y}}[t], {\widetilde{x}}[t] \right) + \frac{1}{t+1} \sum _{k=1}^{K} \chi _k[t] d_k(p_k) \right\} , \\ \rho _t= & {} \frac{1}{t+1} \sum _{k=1}^{K} \sum _{r=0}^{t} \frac{1}{2 \chi _k[r-1]} \left\| \nabla _{p_k} \mathcal {E}(p_1[t], \ldots , p_K[t])\right\| _{k*}^2.\\ \end{aligned}$$

Let us relate the penalty term $h_t$ to Q[t] from Lemma 4.1. For that, we define the Euclidean prox-function $d(p) := \frac{1}{2} \sum _{j=1}^{n} \left( p^{(j)}\right) ^2.$ Note that

$$\begin{aligned}&h_t\left( {\widetilde{y}}[t], {\widetilde{x}}[t]\right) \ge - \min _{p \in \mathbb {R}^n_+} \left\{ \varphi \left( p, \ldots , p, {\widetilde{y}}[t], {\widetilde{x}}[t] \right) + \frac{1}{t+1} \sum _{k=1}^{K} \chi _k[t] d_k(p)\right\} \\&\quad =- \min _{p \in \mathbb {R}^n_+} \left\{ \left\langle p, \sum _{k=1}^{K} {\widetilde{y}}_k[t] - \sum _{i=1}^{I} {\widetilde{x}}_i[t] \right\rangle + \frac{1}{t+1} \sum _{k=1}^{K} \chi _k[t] d_k(p) \right\} \\&\quad \ge - \min _{p \in \mathbb {R}^n_+} \left\{ \left\langle p, \sum _{k=1}^{K} {\widetilde{y}}_k[t] - \sum _{i=1}^{I} {\widetilde{x}}_i[t] \right\rangle + \frac{\sum _{k=1}^{K} \chi _k[t]}{t+1} \frac{1}{\min _{k,j} \zeta _k^{(j)}} d(p) \right\} \\&\quad = \frac{t+1}{\sum _{k=1}^{K} \chi _k[t]} \min _{k,j} \frac{\zeta _k^{(j)}}{2} \sum _{j=1}^{n} \left( -\sum _{k=1}^{K} {\widetilde{y}}^{(j)}_k[t] + \sum _{i=1}^{I} {\widetilde{x}}^{(j)}_i[t] \right) _+^2 = \frac{C_2}{d_t} Q[t], \end{aligned}$$

where $C_2 = \min _{k,j} \frac{\zeta _k^{(j)}}{2}$. Now, we relate the remainder term $\rho _t$ to $b_t$ from Lemma 4.1. For that, let the constant $C_3 > 0$ bound the sequence of kth producer’s excess supplies:

$$\begin{aligned} \Vert \nabla _{p_k} \mathcal {E}(p_1[t], \ldots , p_K[t])\Vert ^2_{k*} \le 2 C_3, \quad t \ge 0, k=1, \ldots , K. \end{aligned}$$

(43)

The existence of $C_3$ in (43) follows from the compactness of production sets $\mathcal {Y}_k, k=1, \ldots , K$, and consumption sets $\mathcal {X}_i, i=1, \ldots , I$ (see Sect. 2). Then, it holds:

$$\begin{aligned} \rho _t =\frac{1}{t+1} \sum _{k=1}^{K} \sum _{r=0}^{t} \frac{1}{2 \chi _k[r-1]} \left\| \nabla _{p_k} \mathcal {E}(p_1[t], \ldots , p_K[t])\right\| _{k*}^2 \le C_3 b_t. \end{aligned}$$

Altogether, substituting this into (42), we get the right-hand side of (28) in Lemma 4.1.

Now, we estimate the duality gap in Lemma 4.1 from below. For that, we apply Lemma 5.1 and Theorem 3.4:

$$\begin{aligned} {\varPhi }[t] - \frac{C_2}{d_t} Q[t]= & {} {\varPhi }\left( \alpha [t], {\widetilde{y}}[t], \beta [t], {\widetilde{x}}[t] \right) - \frac{C_2}{d_t} \sum _{j=1}^{n} \left( -\sum _{k=1}^{K} {\widetilde{y}}^{(j)}_k[t] + \sum _{i=1}^{I} {\widetilde{x}}^{(j)}_i[t] \right) _+^2\\\le & {} \mathop {\max }\limits _{\left( \alpha , {\widetilde{y}}, \beta , {\widetilde{x}} \right) \in \mathcal {A}} {\varPhi }\left( \alpha , {\widetilde{y}}, \beta , {\widetilde{x}} \right) - \frac{C_2}{d_t} \sum _{j=1}^{n} \left( -\sum _{k=1}^{K} {\widetilde{y}}^{(j)}_k + \sum _{i=1}^{I} {\widetilde{x}}^{(j)}_i \right) _+^2 \\\le & {} \mathop {\mathop {\max }\limits _{\left( \alpha , {\widetilde{y}}, \beta , {\widetilde{x}} \right) \in \mathcal {A}}}\limits _{\sum \nolimits _{k=1}^{K} {\widetilde{y}}_k \ge \sum _{i=1}^{I} {\widetilde{x}}_i} {\varPhi }\left( \alpha , {\widetilde{y}}, \beta , {\widetilde{x}} \right) +\frac{d_t}{4C_2} \sum _{j=1}^{n} p^{*(j)} =\mathcal {E}^* + C_1 d_t, \end{aligned}$$

where $C_1 = \frac{\sum \nolimits _{j=1}^{n} p^{*(j)}}{{4C_2}}$ and $p^*$ is the vector of equilibrium prices. Note that Lagrange multipliers for the market feasibility constraint in the adjoint problem (A) coincide with minimizers $p^*$ of the total excessive revenue $\mathcal {E}$. $\square$