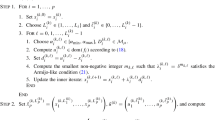Inexact Coordinate Descent: Complexity and Preconditioning

Abstract

One of the key steps at each iteration of a randomized block coordinate descent method consists in determining the update to a block of variables. Existing algorithms assume that in order to compute the update, a particular subproblem is solved exactly. In this work, we relax this requirement and allow for the subproblem to be solved inexactly, leading to an inexact block coordinate descent method. Our approach incorporates the best known results for exact updates as a special case. Moreover, these theoretical guarantees are complemented by practical considerations: the use of iterative techniques to determine the update and the use of preconditioning for further acceleration.

1 Introduction

Due to a dramatic increase in the size of optimization problems being encountered, first-order methods are becoming increasingly popular. These large-scale problems are often highly structured, and it is important for any optimization method to take advantage of the underlying structure. Applications where such problems arise, and where first-order methods have proved successful, include machine learning [1, 2], compressive sensing [3, 4], group lasso [5, 6], matrix completion [7, 8], and truss topology design [9].

Block Coordinate Descent (CD) methods seem a natural choice for these very large-scale problems due to their low memory requirements and low per-iteration computational cost. Furthermore, they are often designed to take advantage of the underlying structure of the optimization problem [10, 11], and many of these algorithms are supported by high probability iteration complexity results [9, 12–15].

More generally, as problem sizes increase, first-order methods are benefiting from revived interest. However, on very large problems, the computation of a single gradient step is expensive, and methods are needed that are able to make progress before a standard gradient algorithm takes a single step. For instance, a randomized variant of the Kaczmarz method for solving linear systems has recently been studied, equipped with iteration complexity bounds [16–18], and found to be surprisingly efficient. This method can be seen as a special case of a more general class of decomposition algorithms, block CD methods, which have recently gained much popularity [12–14, 19–22]. One of the main differences between various (serial) CD schemes is the way in which the coordinate is chosen at each iteration. Traditionally, cyclic schemes [23] and greedy schemes [9] were studied. More recently, a popular alternative is to select coordinates randomly, because the coordinate can be selected cheaply, and useful iteration complexity results can be obtained [14, 20, 21, 24].

Another current trend in this area is to consider methods that incorporate some kind of ‘inexactness,’ perhaps using approximate gradients, or using inexact updates. The notion of an ‘inexact oracle’ was introduced in [25], and complexity estimates for primal, dual, and fast gradient methods applied to smooth convex functions with that inexact oracle are obtained. Further to this work, the same authors describe an intermediate gradient method that uses an inexact oracle [26]. That work is extended in [27] to handle the case of composite functions, where a stochastic inexact oracle is also introduced. A method based on inexact dual gradient information is introduced in [28], while [2] considers the minimization of an unconstrained, convex, and composite function, where error is present in the gradient of the smooth term or in the proximity operator for the non-smooth term. Other works study first-order methods that use inexact updates when the objective function is convex, smooth and unconstrained [29], smooth and constrained [30] or for $\ell _1$-regularized quadratic least squares problem [31]. Finally, work in [32] considers an Inexact Coordinate Descent method for smooth functions, with simple constraints on the blocks of variables.

To the best of our knowledge, at present there are no randomized CD methods supported by high probability iteration complexity results that both (1) incorporate inexact updates and (2) can be applied to a general convex composite problem formulation. The purpose of this work is to bridge this gap.

The first part of this paper focuses on the theoretical aspects of ICD. The problem and our contributions are stated in Sect. 2. In Sect. 3, the assumptions and notation are laid out, and in Sect. 4, the ICD method is presented. In Sect. 5, iteration complexity results for ICD applied to (1) are presented in both the convex and strongly convex cases. Specialized complexity results covering the smooth case are presented in Sect. 6. The second part of the paper considers the practicality of an inexact update. Section 7 provides several examples of how to derive the formulation for the update step subproblem, as well as giving suggestions for algorithms that can be used to solve the subproblem inexactly. Numerical experiments are presented in Sect. 8, and we conclude in Sect. 9.

2 Problem and Contributions

If the block size is larger than one, then determining the update to use at a particular iteration in a block CD method can be computationally expensive. The purpose of this work is to reduce the cost of this step. To achieve this goal, we extend the work in [14] to include the case of an inexact update.

In this work, we study randomized block CD methods applied to the problem of minimizing a composite objective function. That is, a function formed as the sum of a smooth convex and a simple non-smooth convex term:

$$\begin{aligned} \min _{x \in \mathbb {R}^N} \{F(x) :=f(x) + \varPsi (x)\}. \end{aligned}$$

(1)

We assume that (1) has a minimum $(F^* > -\infty )$, f has (block) coordinate Lipschitz gradient, and $\varPsi$ is a (block) separable, proper, closed and convex extended real-valued function (all these concepts are defined precisely in Sect. 3).

Our algorithm—Inexact Coordinate Descent (ICD)—is supported by high probability iteration complexity results: For confidence level $0<\rho <1$ and error tolerance $\epsilon >0$, we give an explicit expression for the number of iterations k, that guarantee that the ICD method produces a random iterate $x_k$ for which $\mathbb {P}(F(x_k)-F^* \le \epsilon ) \ge 1-\rho .$ We will show that in the inexact case that it is not always possible to achieve a solution with small error and/or high confidence.

Our theoretical guarantees are complemented by practical considerations. In Sect. 4.3, we explain our inexactness condition in detail, and in Sect. 4.4 we give examples to show when the inexactness condition is implementable. Furthermore, in Sect. 7 we give several examples, derive the update subproblems, and suggest algorithms that could be used to solve the subproblems inexactly, and some encouraging computational results are presented in Sect. 8. Now, we summarize the main contributions of this work.

2.1 A New Algorithm: Inexact Coordinate Descent (ICD)

In this paper, we propose a new randomized CD method for solving very large convex and composite optimization problems of the form (1), namely the Inexact Coordinate Descent (ICD) method. ICD extends the work of Richtárik and Takáč in [14] (henceforth we refer to their method as Exact CD) in the following way. At each iteration of Exact CD, a block of coordinates i is chosen, and then, a certain subproblem is solved exactly to obtain the (exact) update to apply to the ith block of variables. On the other hand, at each iteration of ICD, that same subproblem is solved to obtain the update to apply to the ith block of variables, but for ICD we allow the subproblem to be solved approximately, leading to an inexact update. There are many reasons why incorporating inexactness is important; we list several now.

• It may be impossible or impractical to compute an exact update. In particular, sometimes the subproblems encountered within Exact CD do not have a closed-form solution, so it is impossible to exactly solve the subproblem/determine an exact update. Moreover, even if a closed-form solution exists, it can sometimes be computationally inefficient to form the exact solution. Therefore, allowing inexact updates extends the range of problems that can be solved using a CD method.

• Iterative methods can be used to compute the update. When a subproblem does have a closed-form solution, Exact CD requires a ‘direct method’ to form the update. For ICD, the update is allowed to be inexact, so iterative methods can be employed. This can be particularly important when the subproblems are linear systems. Indeed, while direct methods require expensive factorizations, for ICD one can employ iterative solvers such as the conjugate gradients method. Therefore, inexact updates, and iterative methods, give the user greater flexibility in how they solve the problem they are facing. (See Sects. 7 and 8 for further details.)

• Inexact updates can decrease the overall runtime. Usually, an inexact solution to a subproblem can be obtained in a shorter amount of time than an exact one. Using ICD, it is possible to determine the solution to (1) in a much shorter amount of time than for Exact CD.

• Inexact updates allow us to study how error propagates through the algorithm. Studying inexact updates is an interesting exercise from a theoretical perspective, because inexact updates allow us to study how error propagates through the algorithm as iterates progress.

2.2 High Probability Iteration Complexity Results

In this work, we also establish iteration complexity results to show that, with high probability (and also in expectation), ICD converges to an $\epsilon$-accurate solution of (1). In Table 1, we summarize some of the main new complexity results obtained in this paper for an inexact update and compare our new results with the complexity results for an exact update presented in [14]. The following notation is used in the table: By $\mu _\phi$, we denote the strong convexity parameter of function $\phi$ (with respect to a certain norm specified later), $\mu = (\mu _f + \mu _\varPsi )/(1 + \mu _\varPsi )$ and $\mathcal{R}_{w}(x_0)$ can be roughly considered to be the distance from $x_0$ to a solution of (1), measured in a specific weighted norm parameterized by the vector w (defined precisely in (10)). The constants are $c_1 = 2n \max \{\mathcal{R}_{w}^2(x_0),F(x_0)-F^*\}, \hat{c}_1 = 2\mathcal{R}_{w}^2(x_0)$, and $c_2 = 2n\mathcal{R}_{w}^2(x_0)/\epsilon$, and n is the number of blocks. Parameters $\alpha , \beta \ge 0$ control the level of inexactness (to be defined precisely in Sect. 4.2), and u and $\hat{u}$ are constants depending on $\alpha$, $\beta$ and $c_1$, and $\alpha$, $\beta$ and $\hat{c}_1$, respectively.

Table 1 Comparison of the iteration complexity results for CD methods using an exact or an inexact update

Table 1 shows that for fixed $\epsilon$ and $\rho$, an inexact method may require slightly more iterations than an exact one. However, it is expected that in certain situations, an inexact update will be significantly cheaper to compute than an exact update, leading to better overall running time.

2.3 Generalization of Existing Results

The ICD method developed in this paper extends the Exact CD method presented in [14], by allowing inexact updates to be utilized. Moreover, the new complexity results obtained in this paper for ICD generalize those for the exact method. Specifically, ICD allows inexact updates, corresponding to nonnegative inexactness parameters $\alpha , \beta \ge 0$. However, if we set the inexactness parameters to zero ($\alpha = \beta = 0$), then ICD enforces exact updates, and we recover the Exact CD method presented in [14] and its corresponding complexity results. This can be verified by inspecting Table 1. If we substitute $\alpha = \beta = 0$ (taking limits where appropriate, which also results in $u = \hat{u} = 0$) into our complexity results (the third column), then we recover the complexity results established in [14] (shown in the second column of Table 1). Furthermore, if $\beta = 0$ and $\alpha >0$, then the ‘log term’ for ICD is the same as for Exact CD, but the constant is different. On the other hand, in the strongly convex case, if $\alpha =0$ and $\beta > 0$, then the constants are the same for ICD and for Exact CD, but the ‘log terms’ are different.

3 Assumptions and Notation

In this section, we introduce the notation and definitions that are used throughout the paper. We follow the standard setup and notation used for block coordinate descent methods, as presented, for example, in [13] and [14].

Block structure of $\mathbb {R}^N$. The problem under consideration is assumed to have block structure, and this is modeled by decomposing the space $\mathbb {R}^N$ into n subspaces as follows. Let $U \in \mathbb {R}^{N \times N}$ be a column permutation of the $N \times N$ identity matrix and further let $U = [U_1,U_2,\dots ,U_n]$ be a decomposition of U into n submatrices, where $U_i$ is $N \times N_i$ and $\sum _{i=1}^n N_i = N$. Clearly (e.g., see [20] for a brief proof) any vector $x \in \mathbb {R}^N$ can be written uniquely as

$$\begin{aligned} \textstyle x = \sum \limits _{i=1}^n U_ix^{(i)},\quad \text {where}\;\; x^{(i)} :=U_i^Tx \in \mathbb {R}^{N_i}. \end{aligned}$$

(2)

For simplicity, we will sometimes write $x = (x^{(1)},x^{(2)},\dots ,x^{(n)})$ instead of (2).

Let $\langle \cdot ,\cdot \rangle$ denote the standard Euclidean dot product. We equip $\mathbb {R}^{N_i}$ with a pair of conjugate norms, induced by a quadratic form involving a symmetric, positive definite matrix $B_i$:

$$\begin{aligned} \Vert t\Vert _{(i)} :=\langle B_it,t \rangle ^{\frac{1}{2}}, \qquad \Vert t\Vert _{(i)}^* = \langle B_i^{-1}t,t \rangle ^{\frac{1}{2}}, \qquad t \in \mathbb {R}^{N_i}. \end{aligned}$$

(3)

Smoothness of f. We assume that the gradient of f is block Lipschitz, uniformly in x, with positive constants $l_1,\dots ,l_n$. So, for all $x \in \mathbb {R}^N$, $t \in \mathbb {R}^{N_i}$ and $i\in \{1,\dots ,n\}$, we have $\Vert \nabla _i f(x + U_i t) - \nabla _i f(x) \Vert _{(i)}^* \le l_i \Vert t\Vert _{(i)},$ where $\nabla _i f(x) :=U_i^T\nabla f(x) \in \mathbb {R}^{N_i}$ (see (2)). An important consequence of this Lipschitz continuity assumption is the following standard inequality [33, p. 57]:

$$\begin{aligned} f(x+U_i t) \le f(x) + \langle \nabla _i f(x), t\rangle + \tfrac{l_i}{2}\Vert t\Vert _{(i)}^2. \end{aligned}$$

(4)

Block separability of $\varPsi$. The function $\varPsi :\mathbb {R}^N \rightarrow \mathbb {R}\cup \{+\infty \}$ is assumed to be block separable. That is, for closed and convex functions $\varPsi _i: \mathbb {R}^{N_i} \rightarrow \mathbb {R}\cup \{+\infty \}$, we assume that $\varPsi$ can be decomposed as:

$$\begin{aligned} \textstyle \varPsi (x) = \sum \limits _{i=1}^n \varPsi _i (x^{(i)}). \end{aligned}$$

(5)

Norms on $\mathbb {R}^N$. For fixed positive scalars $w_1,\dots ,w_n$, let $w = (w_1,\dots ,w_n)$ and define a pair of conjugate norms in $\mathbb {R}^N$ by

$$\begin{aligned} \textstyle \Vert x\Vert _w^2 :=\sum \limits _{i=1}^n w_i \Vert x^{(i)}\Vert ^2_{(i)}, \qquad (\Vert y\Vert _w^*)^2 :=\sum \limits _{i=1}^n w_i^{-1} (\Vert y^{(i)}\Vert ^*_{(i)})^2. \end{aligned}$$

(6)

In our analysis, we often use $w = l$ (for $\varPsi \ne 0$) and/or $w = lp^{-1}$ (for $\varPsi =0$), where $l= (l_1,\dots ,l_n)$ and $p = (p_1,\dots ,p_n)$ denote vectors of Lipschitz constants and positive probabilities, respectively, and $lp^{-1} \equiv (l_1/p_1,\dots , l_n/p_n)$.

Strong convexity of F. A function $\phi : \mathbb {R}^N \rightarrow \mathbb {R}\cup \{+ \infty \}$ is strongly convex w.r.t. $\Vert \cdot \Vert _w$ with convexity parameter $\mu _{\phi }(w) > 0$, if, for all $x,y \in {{\mathrm{dom}}}\phi$,

$$\begin{aligned} \phi (y) \ge \phi (x) + \langle \phi ^{\prime }(x),y-x \rangle + \tfrac{\mu _{\phi }(w)}{2}\Vert y-x\Vert _w^2, \end{aligned}$$

(7)

where $\phi ^{\prime }$ is any subgradient of $\phi$ at x. The case with $\mu _{\phi }(w)= 0$ reduces to convexity. We will also make use of the following characterization of strong convexity. For all $x,y \in {{\mathrm{dom}}}\phi$ and $\lambda \in [0,1]$,

$$\begin{aligned} \phi \big (\lambda x + (1-\lambda ) y \big ) \; \le \; \lambda \phi (x) + (1-\lambda )\phi (y) - \tfrac{\mu _\phi (w)\lambda (1-\lambda )}{2}\Vert x-y\Vert _w^2. \end{aligned}$$

(8)

In some of the results presented in this work, we assume that F is strongly convex. Strong convexity of F may come from f or $\varPsi$ or both, and we will write $\mu _f(w)$ (respectively, $\mu _{\varPsi }(w)$) for the strong convexity parameter of f (resp. $\varPsi$), with respect to $\Vert \cdot \Vert _w$. Following from (4) and (7), we have

$$\begin{aligned} \mu _F(w) \ge \mu _f(w) + \mu _\varPsi (w),\quad \mu _f(l)\le 1, \quad \text {and} \quad \mu _f(lp^{-1}) \le 1. \end{aligned}$$

(9)

Level set radius. The set of optimal solutions of (1) is denoted by $X^*$, and $x^*$ is any element of that set. We define

$$\begin{aligned} \mathcal {R}_w(x) :=\max _y \max _{x^* \in X^*} \{ \Vert y - x^*\Vert _w : F(y) \le F(x) \}, \end{aligned}$$

(10)

which is a measure of the size of the level set of F given by x. We assume that $\mathcal {R}_w(x_0)$ is finite for the initial iterate $x_0$.

4 The Algorithm

Let us start by presenting the algorithm; a detailed description will follow. In the algorithm description, $\mathbb {R}_+^n$ denotes a vector in $\mathbb {R}^n$ with nonnegative entries. The vector $\delta _k = (\delta _k^{(1)},\dots ,\delta _k^{(n)}) \in \mathbb {R}_+^n$, relates to/controls the inexactness in the computed update (Step 3); this will be defined precisely in Sect. 4.2.

Remark 4.1

We make the following remarks regarding ICD (Algorithm 1).

• 1. In Step 4 of Algorithm 1, block $i \in \{1,\dots ,n\}$ is selected with probability $p_i>0$. For convex composite functions (i.e., $\psi (x) \ne 0$ in (1)), the probabilities must be uniform ($p_1 = \dots = p_n = \frac{1}{n}$), while for smooth functions (i.e., $\psi (x) = 0$ in (1)) the probability distributions can be more general.

• 2. Conditions on all the parameters of Algorithm 1 are made explicit in the theoretical results presented throughout the remainder of this paper.

4.1 Generic Description

Given iterate $x_k \in \mathbb {R}^N$, Algorithm 1 picks block $i \in \{1,\dots ,n\}$ with probability $p_i$, computes the update vector $T^{(i)}_{\delta _k}(x_k)\in \mathbb {R}^{N_i}$ (we describe how this is computed later) and then adds it to the ith block of $x_k$, producing the new iterate $x_{k+1}$. The iterates $\{x_k\}$ are random vectors, and the values $\{F(x_k)\}$ are random variables. The update vector depends on $x_k$, the current iterate, and on $\delta _k$, a vector of parameters controlling the ‘level of inexactness’ with which $T^{(i)}_{\delta _k}(x_k)$ is computed. The rest of this section is devoted to giving a precise definition of $T^{(i)}_{\delta _k}(x_k)$. From (1) and (4) we have, for all $x\in \mathbb {R}^N$, $i \in \{1,\dots ,n\}$ and $t\in \mathbb {R}^{N_i}$ the following upper bound on $F(x+U_i t)$:

$$\begin{aligned} F(x + U_it) = f(x+U_it) + \varPsi (x+U_i t) \le f(x) + V_i(x,t) + \varPsi _{-i}(x), \end{aligned}$$

(11)

where $\varPsi _{-i}(x) :=\sum _{j \ne i} \varPsi _j(x^{(j)})$ and

$$\begin{aligned} V_i(x,t) :=\langle \nabla _i f(x),t \rangle + \tfrac{l_i}{2}\Vert t\Vert _{(i)}^2 + \varPsi _i(x^{(i)}+t). \end{aligned}$$

(12)

The inexact update computed in Step 5 of Algorithm 1 is the inexact minimizer of the upper bound (11) on $F(x_k+U_it)$ (to be defined precisely below). However, since only the second term of this bound depends on t, the update is computed by minimizing, inexactly, $V_i(x,t)$ in t.

4.2 Inexact Update

The approach of this paper best applies to situations in which it is much easier to approximately minimize $t\mapsto V_i(x,t)$ than to either (1) approximately minimize $t\mapsto F(x+ U_i t)$ and/or (2) exactly minimize $t \mapsto V_i(x,t)$. For $x\in \mathbb {R}^N$ and $\delta = (\delta ^{(1)},\dots , \delta ^{(n)}) \ge 0$, we define $T_{\delta }(x) :=(T_{\delta }^{(1)}(x),\dots , T_{\delta }^{(n)}(x))\in \mathbb {R}^N$, to be any vector satisfying

$$\begin{aligned} V_i(x,T_{\delta }^{(i)}(x)) \le \min \left\{ V_i(x,0), \delta ^{(i)}+ \min _{t \in \mathbb {R}^{N_i}} V_i(x,t)\right\} , \quad i = 1,\dots ,n. \end{aligned}$$

(13)

(Here we allow for an abuse of notation — $\delta ^{(i)}$ is a scalar, rather than a vector in $\mathbb {R}^{N_i}$ as $x^{(i)}$ for $x\in \mathbb {R}^N$—because we wish to emphasize that the scalar $\delta ^{(i)}$ is associated with the ith block.) That is, we require that the inexact update $T_\delta ^{(i)}(x)$ to the ith block of x is (1) no worse than a vacuous update and that it is (2) close to the optimal update $T_0^{(i)}(x)=\arg \min _{t} V_i(x,t)$, where the degree of suboptimality/inexactness is bounded by $\delta ^{(i)}$.

The next lemma shows that (13) leads to a monotonic algorithm.

Lemma 4.1

For all $x\in \mathbb {R}^N, \delta \in \mathbb {R}^n_+$ and $i\in \{1,\dots ,n\}$, we have that $F(x + U_i T_{\delta }^{(i)}(x)) \le F(x)$.

Proof

By (11), $F(x+ U_i T_{\delta }^{(i)}(x)) \le f(x) + V_i(x, T_\delta ^{(i)}(x)) + \varPsi _{-i}(x)$. It remains to apply (13) and (12). $\square$

Furthermore, in this work we provide iteration complexity results for ICD, where $\delta _k=(\delta _k^{(1)},\dots ,\delta _k^{(n)})$ is chosen in such a way that the expected suboptimality is bounded above by a linear function of the residual $F(x_k)-F^*$. That is, we have the following assumption.

Assumption 4.1

For constants $\alpha ,\beta \ge 0$, and positive probabilities $p_1,\dots ,p_n$, $\delta _k= (\delta _k^{(1)},\dots , \delta _k^{(n)})$ satisfies

$$\begin{aligned} \textstyle \bar{\delta }_k :=\sum \limits _{i=1}^n p_i \delta _k^{(i)} \le \alpha (F(x_k)-F^*) + \beta . \end{aligned}$$

(14)

Notice that, for instance, Assumption 4.1 holds if we require that, for all blocks i and iterations k, $\delta _k^{(i)}\le \alpha (F(x_k)-F^*)+ \beta$.

The motivation for allowing inexact updates of the form (13) is that calculating exact updates is impossible in some cases (e.g., not all problems have a closed-form solution) and computationally intractable in others. Moreover, iterative methods can be used to solve for an inexact update $T_{\delta }^{(i)}(x)$, thus significantly expanding the range of problems that can be successfully tackled by CD. In this case, there is an outer CD loop, and an inner iterative loop to determine the update. Assumption 4.1 shows that the stopping tolerance on the inner loop must be bounded above via (14).

CD methods provide a mechanism to break up very large-/huge-scale problem into smaller pieces, which are a fraction of the total dimension. Moreover, often the subproblems that arise to solve for the update have a similar/the same form as the original huge-scale problem. (See the numerical experiments in Sect. 8, and the examples given in Sect. 7.) There are many iterative methods that cannot scale up to the original huge dimensional problem, but are excellent at solving the medium-scale update subproblems. ICD allows these algorithms to solve for the update at each iteration, and if the updates are solved efficiently, then the overall ICD algorithm running time is kept low.

4.3 The Role of $\alpha$ and $\beta$ in ICD

The condition (13) shows that the updates in ICD are inexact, while Assumption 4.1 gives the level of inexactness that is allowed in the computed update. Moreover, Assumption 4.1 allows us to provide a unified analysis; formulating the error/inexactness expression in this general way (14) gives insight into the role of both multiplicative and additive error, and how this error propagates through the algorithm as iterates progress.

Formulation (14) is interesting from a theoretical perspective because it allows us to present a sensitivity analysis for ICD, which is interesting in its own right. However, we stress that (13), coupled with Assumption 4.1, is much more than just a technical tool; $\alpha$ and $\beta$ are actually parameters of ICD (Algorithm 1) that can be assigned explicit numerical values in many cases.

We now explain (13), Assumption 4.1 and the role of parameters $\alpha$ and $\beta$ in slightly more detail. (Note that $\alpha$ and $\beta$ must be chosen sufficiently small to guarantee convergence of the ICD algorithm. However, we postpone discussion of the magnitude of $\alpha$ and $\beta$ until Sect. 4.5.) There are four cases.

• 1. Case I: $\alpha = \beta = 0$. This corresponds to the exact case where no error is allowed in the computed update.

• 2. Case II: $\alpha = 0, \beta >0$. This case corresponds to additive error only, where the error level $\beta >0$ is fixed at the start of Algorithm 1. In this case, (13) and (14) show that the error allowed in the inexact update $T_{\delta }^{(i)}(x_k)$ is on average $\beta$. For example, one can set $\delta _k^{(i)}= \beta$ for all blocks i and all iterations k, so that (14) becomes $\bar{\delta }_k = \sum _i p_i \beta = \beta$. The tolerance allowable on each block need not be the same; if one sets $\delta _k^{(i)}\le \beta$ for all blocks i and iterates k, then $\bar{\delta }_k \le \beta$, so (14) holds true. Moreover, one need not set $\delta _k^{(i)}>0$ for all i, so that the update vector $T_{\delta }^{(i)}(x_k)$ could be exact for some blocks ($\delta _k^{(i)}=0$) and inexact for others ($\delta _k^{(j)} >0$). (This may be sensible, for example, when $\varPsi _i(x^{(i)}) \ne \varPsi _j(x^{(j)})$ for some $i\ne j$ and that (12) has a closed-form solution for $T^{(i)}(x_k)$ but not for $T^{(j)}(x_k)$.) Furthermore, consider the extreme case where only one block update is inexact $T_{\delta }^{(i)}(x_k)$, ($T_{0}^{(j)}(x_k)$ for all $j\ne i$). If the coordinates are selected with uniform probability, then the inexactness level on block i can be as large as $\delta _k^{(i)}= n \beta$ and Assumption 4.1 holds.

• 3. Case III: $\alpha > 0, \beta = 0$. In this case, only multiplicative error is allowed in the computed update $T_{\delta }^{(i)}(x_k)$, where the error allowed in the update at iteration k is related to the error in the function value ($F(x_k)-F^*$). The multiplicative error level $\alpha$ is fixed at the start of Algorithm 1, and $\alpha (F(x_k) - F^*)$ is an upper bound on the average error in the update $T_{\delta }^{(i)}(x_k)$ over all blocks i at iteration k. In particular, setting $\delta _k^{(i)}\le \alpha (F(x_k)-F^*)$ for all i and k satisfies Assumption 4.1. As for Case II, one may set $\delta _k^{(i)}= 0$ for some block(s) i, or set $\delta _k^{(i)}> \alpha (F(x_k)-F^*)$ for some blocks i and iterations k as long as Assumption 4.1 is satisfied.

• 4. Case IV: $\alpha ,\beta > 0$. This is the most general case, corresponding to the inclusion of both multiplicative ($\alpha$) and additive ($\beta$) error. Assumption 4.1 is satisfied whenever $\delta _k^{(i)}$ obeys $\delta _k^{(i)}\le \alpha (F(x_k)-F^*)+\beta$. Moreover, as for Cases II and III, one may set $\delta _k^{(i)}= 0$ for some block(s) i, or set $\delta _k^{(i)}> \alpha (F(x_k)-F^*)$ for some blocks i and iterations k as long as Assumption 4.1 is satisfied. As iterations progress, the multiplicative error may become dominated by the additive error, in the sense that $\alpha (F(x_k)-F^*) \rightarrow 0$ as $k \rightarrow \infty$, so the upper bound on $\bar{\delta _k}$ tends to $\beta$.

Cases I–IV above show that the parameters $\alpha$ and $\beta$ directly relate to the stopping criterion used in the algorithm employed to solve for the update $T_{\delta }^{(i)}(x_k)$ at each iteration of ICD. The following section gives examples of algorithms that can be used within ICD, where $\alpha$ and $\beta$ can be given explicit numerical values and the stopping tolerances are verifiable.

4.4 Computing the Inexact Update

Here, we focus on the computation of the inexact update (Step 5 of Algorithm 1). We discuss several cases where Assumption 4.1 can be verified and thus provide specific instances to show that ICD is indeed implementable.

• 1. A primal–dual algorithm: Assume that we utilize a primal–dual algorithm to minimize $V_i(x_k,t)$. There are many such methods (e.g., stochastic dual coordinate ascent), and the structure/size of the subproblem dictates what choices are suitable. In such a case, the level of inexactness can be directly controlled by monitoring the duality gap. Hence, (13) is easy to satisfy for any choice of $\delta _k^{(i)}$. Indeed, we simply accept $T_{\delta _k}^{(i)}$, for which

  $$\begin{aligned} V_i(x_k,T_{\delta _k}^{(i)})) - V_i(x_k,T_0^{(i)}) \le V_i(x_k,T_{\delta _k}^{(i)})) - V_i^{\text {DUAL}}(x_k,T_{\delta _k}^{(i)}))\le \delta _k^{(i)}, \end{aligned}$$

  (15)

  where $V_i^{\text {DUAL}}(x_k,T_{\delta _k}^{(i)}))$ is the value of the dual at the point $T_{\delta _k}^{(i)}$. Moreover, if we set $\alpha =0$ and $\beta =\sum _i p_i \delta _k^{(i)}$, then Assumption 4.1 is satisfied.

• 2. $F^*$ is known: There are many problem instances when $F^*$ is known a priori, so the bound $F(x_k)-F^*$ is computable at every iteration, and subsequently multiplicative error can be incorporated into ICD (i.e, $\alpha >0$). This is the case, for example, when solving a consistent system of equations (solving a least squares problem that is known to have optimal value 0), where $F^*=0$, so that $F(x_k)-F^* = F(x_k)$.

• 3. A heuristic when $F^*$ is unknown: If $F^*$ is unknown, one can use a heuristic argument to incorporate multiplicative error into ICD. Suppose we have a point $x_k$ and we wish to compute $x_{k+1}$ via an inexact update. Clearly, $F(x_{k+1})\ge F^*$ for any $x_{k+1}$, so $F(x_k) - F(x_{k+1})\le F(x_k) - F^*.$ Obviously, we do not know $F(x_{k+1})$ until $x_{k+1}$ has been computed. Rather, in practice one could simply not set $\delta _k$, but compute some trial point $x_{k+1}'$ using an inexact update anyway. Then, by computing the difference $F(x_k) - F(x_{k+1}')$, we can check whether, in hindsight, the assumption was satisfied for the trial point $x_{k+1}'$ for some $\alpha >0$. We remark that, even though computing function values explicitly can be expensive, computing the difference of function values (i.e., $F(x_k) - F(x_{k+1})$) need not be. (See Sect. 7 for further details.)

4.5 Technical Result

The following result plays a key role in the complexity analysis of ICD. Indeed, the theorem adapts Theorem 1 in [14] to the setting of inexactness, and the proof follows similar arguments to those used in [14].

Theorem 4.1

Fix $x_0 \in \mathbb {R}^N$ and let $\{x_k\}_{k \ge 0}$ be a sequence of random vectors in $\mathbb {R}^N$ with $x_{k+1}$ depending on $x_k$ only. Let $\varphi :\mathbb {R}^N \rightarrow \mathbb {R}$ be a nonnegative function, define $\xi _k :=\varphi (x_k)$ and assume that $\{\xi _k\}_{k \ge 0}$ is non-increasing. Furthermore, let $0<\rho <1$, $\epsilon >0$ and $\alpha ,\beta \ge 0$ be such that one of the following two conditions holds:

• (i) $\mathbb {E}[\xi _{k+1}\;|\;x_k] \le (1+\alpha ) \xi _k - \tfrac{\xi _k^2}{c_1} + \beta$, for all $k\ge 0$, where $c_1>0$, $\tfrac{c_1}{2}\left( \alpha + \sqrt{\alpha ^2 + \tfrac{4\beta }{c_1 \rho }}\right) < \epsilon < \min \{(1+\alpha )c_1,\xi _0\}$ and $\sigma :=\sqrt{\alpha ^2 + \tfrac{4\beta }{c_1}} < 1$;

• (ii) $\mathbb {E}[\xi _{k+1}\;|\;x_k] \le \left( 1 + \alpha - \tfrac{1}{c_2}\right) \xi _k + \beta ,$ for all $k\ge 0$ for which $\xi _k \ge \epsilon$, where $\alpha c_2 < 1\le (1+\alpha )c_2$, and $\tfrac{\beta c_2}{\rho (1 - \alpha c_2)} < \epsilon < \xi _0$.

If (i) holds and we define $u :=\tfrac{c_1}{2}(\alpha + \sigma )$ and $v :=\frac{c_1}{\epsilon - \alpha c_1}$ and choose

$$\begin{aligned} K\ge v \log \left( \tfrac{\epsilon - \beta v}{\epsilon \rho - \beta v}\right) + \min \left\{ \tfrac{1}{\sigma } \log \left( \tfrac{\xi _0-u}{\epsilon -u} \right) , \tfrac{c_1}{\epsilon -u} -\tfrac{c_1}{\xi _0-u} \right\} + 2, \end{aligned}$$

(16)

(where the second term in the minimum is chosen if $\sigma =0$), or if (ii) holds and we choose

$$\begin{aligned} K \ge \tfrac{c_2}{1-\alpha c_2} \log \left( \tfrac{\xi _0 - \tfrac{\beta c_2}{1-\alpha c_2}}{\epsilon \rho - \tfrac{\beta c_2}{1-\alpha c_2}}\right) , \end{aligned}$$

(17)

then $\mathbb {P}(\xi _{K}\le \epsilon ) \ge 1- \rho$.

Proof

First, notice that the thresholded sequence $\{\xi _k^{\epsilon }\}_{k \ge 0}$, defined by

$$\begin{aligned} \xi _k^{\epsilon } :={\left\{ \begin{array}{ll} 0, &{} \text {if } \; \xi _k < \epsilon ,\\ \xi _k, &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

(18)

satisfies $\xi _k^{\epsilon } > \epsilon \Leftrightarrow \xi _k > \epsilon$. Therefore, $\mathbb {P}(\xi _k \ge \epsilon ) =\mathbb {P}(\xi _k^{\epsilon } \ge \epsilon ) \le \frac{\mathbb {E}[\xi _k^{\epsilon }]}{\epsilon }$ by Markov’s inequality. Thus, letting $\theta _k :=\mathbb {E}[\xi _k^{\epsilon }]$, it suffices to show that

$$\begin{aligned} \theta _K \le \epsilon \rho . \end{aligned}$$

(19)

(The rationale behind this ‘thresholding trick’ is that the sequence $\mathbb {E}[\xi _k^\epsilon ]$ decreases faster than $\mathbb {E}[\xi _k]$ and hence will reach $\epsilon \rho$ sooner.) Assume now that (i) holds. It can be shown (e.g., Theorem 1 of [14] with $\alpha =\beta = 0$) that

$$\begin{aligned} \mathbb {E}[\xi _{k+1}^{\epsilon }\;|\;x_k] \le (1+\alpha )\xi _{k}^{\epsilon } - \tfrac{(\xi _{k}^{\epsilon })^2}{c_1} + \beta , \quad \mathbb {E}[\xi _{k+1}^{\epsilon }\;|\;x_k] \le \left( 1 + \alpha - \tfrac{\epsilon }{c_1}\right) \xi _{k}^{\epsilon } + \beta . \end{aligned}$$

(20)

By taking expectations in (20) and using Jensen’s inequality, we obtain

$$\begin{aligned} \theta _{k+1}\le & {} (1+\alpha )\theta _k - \tfrac{\theta _k^2}{c_1} + \beta , \quad k\ge 0,\end{aligned}$$

(21)

$$\begin{aligned} \theta _{k+1}\le & {} \Big (1+\alpha -\tfrac{\epsilon }{c_1}\Big )\theta _k + \beta , \quad k\ge 0. \end{aligned}$$

(22)

Notice that (21) is better than (22) precisely when $\theta _k > \epsilon$. It is easy to see that $(1+\alpha )\theta _k - \tfrac{\theta _k^2}{c_1} + \beta \le \theta _k$ holds if and only if $\theta _k \ge u$. In other words, (21) leads to $\theta _{k+1}$, that is better than $\theta _k$ only for $\theta _k \ge u$. We will now compute $k=k_1$, for which $u <\theta _k \le \epsilon$. Inequality (21) can be equivalently written as

$$\begin{aligned} \theta _{k+1} - u \le (1-\sigma )(\theta _k - u) - \tfrac{(\theta _k-u)^2}{c_1}, \quad k \ge 0, \end{aligned}$$

(23)

where $\sigma <1$. Writing (21) in the form (23) eliminates the constant term $\beta$, which allows us to provide a simple analysis. (Moreover, this ‘shifted’ form leads to a better result; see the remarks after the Theorem for details.) Letting $\hat{\theta }_k :=\theta _k -u$, by monotonicity we have $\hat{\theta }_{k+1}\hat{\theta }_k \le \hat{\theta }_k^2$, whence

$$\begin{aligned} \tfrac{1-\sigma }{\hat{\theta }_{k+1}} - \tfrac{1}{\hat{\theta }_k} = \tfrac{(1-\sigma )\hat{\theta }_k - \hat{\theta }_{k+1}}{\hat{\theta }_{k+1}\hat{\theta }_k} \ge \tfrac{(1-\sigma )\hat{\theta }_k - \hat{\theta }_{k+1}}{\hat{\theta }_k^2} \overset{(23)}{\ge } \tfrac{1}{c_1}. \end{aligned}$$

(24)

If we choose $r\in \{1,\tfrac{1}{1-\sigma }\}$, then

$$\begin{aligned} \tfrac{1}{\hat{\theta }_k} \overset{(24)}{\ge } \left( \tfrac{r}{\hat{\theta }_{k-1}} + \tfrac{r}{c_1}\right) \ge \tfrac{r^k}{\hat{\theta }_0} + \tfrac{1}{c_1} \sum _{j=1}^{k} r^j = {\left\{ \begin{array}{ll}r^k \left( \tfrac{1}{\xi _0-u} + \tfrac{1}{c_1\sigma }\right) - \tfrac{1}{c_1\sigma }, &{} r=\tfrac{1}{1-\sigma }\\ \tfrac{1}{\xi _0-u} + \tfrac{k}{c_1}, &{} r=1.\end{array}\right. } \end{aligned}$$

In particular, using the above estimate with $r=1$ and $r=\tfrac{1}{1-\sigma }$ gives

$$\begin{aligned} \hat{\theta }_{k_1} \le \epsilon - u \qquad (\text {and hence } \theta _{k_1} \le \epsilon ) \end{aligned}$$

(25)

for

$$\begin{aligned} k_1 := \min \left\{ \left\lceil \log \left( \frac{\frac{1}{\epsilon -u} + \frac{1}{c_1\sigma }}{\frac{1}{\xi _0-u} + \frac{1}{c_1\sigma }}\right) / \log \left( \frac{1}{1-\sigma }\right) \right\rceil , \left\lceil \frac{c_1}{\epsilon -u} -\frac{c_1}{\xi _0-u} \right\rceil \right\} , \end{aligned}$$

(26)

where the left term in (26) applies when $\sigma >0$ only.

Applying the inequalities (i) $\lceil t \rceil \le 1 + t$; (ii) $\log (\tfrac{1}{1-t})\ge t$ (which holds for $0<t<1$; we use the inverse version, which is surprisingly tight for small t); and (iii) the fact that $t \mapsto \tfrac{C+t}{D+t}$ is decreasing on $[0,\infty [$ if $C\ge D > 0$, we obtain

$$\begin{aligned} k_1 \ge 1 + \min \left\{ \tfrac{1}{\sigma } \log \left( \tfrac{\xi _0-u}{\epsilon -u} \right) , \tfrac{c_1}{\epsilon -u} -\tfrac{c_1}{\xi _0-u} \right\} . \end{aligned}$$

(27)

Letting $\gamma :=1-\tfrac{\epsilon - \alpha c_1}{c_1}$ (notice that $0<\gamma <1$), for any $k_2\ge 0$ we have

$$\begin{aligned} \theta _{k_1 + k_2}&\overset{(22)}{\le } \gamma \theta _{ k_1 + k_2 - 1} + \beta \le \gamma ^{k_2} \theta _{k_1 } + \beta (\gamma ^{ k_2 -1} +\gamma ^{ k_2 -2}+ \cdots + 1) \nonumber \\&\overset{(25)}{\le } \gamma ^{k_2} \epsilon + \beta \tfrac{1-\gamma ^{k_2}}{1-\gamma } = \gamma ^{k_2}\left( \epsilon - \tfrac{\beta }{1-\gamma }\right) + \tfrac{\beta }{1-\gamma }. \end{aligned}$$

(28)

In (28), the second to last term can be made as small as we like (by taking $k_2$ large), but we can never force $\theta _{k_1 + k_2} \le \tfrac{\beta }{1-\gamma }$. Therefore, in order to establish (19), we need to ensure that $\tfrac{\beta c_1}{\epsilon - \alpha c_1} < \epsilon \rho$. Rearranging this gives the condition $\tfrac{c_1}{2}(\alpha + \sqrt{\alpha ^2 +\frac{4\beta }{c_1 \rho }}) < \epsilon$, which holds by assumption. Now we can find $k_2$, for which the right-hand side in (28) is at most $\epsilon \rho$:

$$\begin{aligned} k_2 :=\left\lceil \log \left( \frac{\epsilon - \tfrac{\beta }{1-\gamma }}{\epsilon \rho - \tfrac{\beta }{1-\gamma }}\right) / \log \left( \frac{1}{\gamma } \right) \right\rceil \le 1+ \frac{c_1}{\epsilon - \alpha c_1} \log \left( \frac{\epsilon - \frac{\beta c_1}{\epsilon - \alpha c_1}}{\epsilon \rho - \frac{\beta c_1}{\epsilon - \alpha c_1}}\right) . \end{aligned}$$

(29)

In view of (19), it is enough to take $K = k_1+k_2$ iterations. The expression in (16) is obtained by adding the upper bounds on $k_1$ and $k_2$ in (27) and (29).

Now assume that property (ii) holds. By a similar argument as that leading to (20), we obtain

$$\begin{aligned} \theta _K\le & {} \left( 1-\tfrac{1-\alpha c_2}{c_2}\right) \theta _{K-1} + \beta \le \textstyle \left( 1-\tfrac{1-\alpha c_2}{c_2}\right) ^K\theta _0 + \beta \sum \limits _{j=0}^{K-1}\left( 1-\tfrac{1-\alpha c_2}{c_2}\right) ^j \\\le & {} \left( 1-\tfrac{1-\alpha c_2}{c_2}\right) ^K\left( \theta _0 - \tfrac{\beta c_2}{1-\alpha c_2}\right) + \tfrac{\beta c_2}{1-\alpha c_2} \overset{(17)}{\le } \epsilon \rho . \end{aligned}$$

The proof follows by taking K given by (17). $\square$

Let us now comment on several aspects of the above result:

• 1. Usage. We will use Theorem 4.1 to finish the proofs of the complexity results in Sect. 5, with $\xi _k = \varphi (x_k) := F(x_k)-F^*$, where $\{x_k\}$ is the random process generated by ICD.

• 2. Monotonicity and Non-negativity. The monotonicity assumption in Theorem 4.1 is, for the choice of $x_k$ and $\varphi$ described in 1, satisfied by Lemma 4.1. Non-negativity is satisfied automatically since $F(x_k) \ge F^*$ for all $x_k$.

• 3. Best of two. In (26), we see that the first term applies when $\sigma >0$ only. If $\sigma = 0$, then $u=0$, and subsequently the second term in (26) applies, which corresponds to the exact case. If $\sigma >0$ is very small (so $u \ne 0$), the iteration complexity result still may be better if the second term is used.

• 4. Generalization. For $\alpha = \beta =0$, (16) recovers $\frac{c_1}{\epsilon }(1 + \log \frac{1}{\rho }) + 2 - \tfrac{c_1}{\xi _0}$, which is the result proved in Theorem 1(i) in [14], while (17) recovers $c_2 \log ((F(x_0)-F^*)/\epsilon \rho )$, which is the result proved in Theorem 1(ii) in [14]. Since the last term in (16) is negative, the theorem holds also if we ignore it. This is what we have done, for simplicity, in Table 1.

• 5. Two lower bounds on $\epsilon$. The inequality $\epsilon > \tfrac{c_1}{2}\left( \alpha + \sqrt{\alpha ^2 + \tfrac{4\beta }{\rho c_1}}\right)$ (see Theorem 4.1(i)) is equivalent to $\epsilon > \tfrac{\beta c_1}{\rho (\epsilon - \alpha c_1)}$. Note the similarity of the last expression and the lower bound on $\epsilon$ in part (ii) of the theorem. We can see that the lower bound on $\epsilon$ is smaller (and hence, is less restrictive) in (ii) than in (i), provided that $c_1=c_2$.

• 6. Two analyses. Analyzing the ‘shifted’ form (23) leads to a better result than analyzing (21) directly, even when $\beta = 0$. Consider the case $\beta =0$, so $\sigma =\alpha$ and $u=\alpha c_1$. From (24) $\theta _{k+1} \le A :=\alpha c_1 + (1-\alpha )/(\tfrac{1}{\theta _k-\alpha c_1} + \tfrac{1}{c_1}),$ whereas analyzing (21) directly yields $\theta _{k+1} \le B :=(1+\alpha )/(\tfrac{1}{\theta _k} + \tfrac{1}{c_1}).$ It can be shown that $A\le B$, with equality if $\alpha = 0$.

• 7. High accuracy with high probability. In the exact case, the iteration complexity results hold for any error tolerance $\epsilon >0$ and confidence $0<\rho <1$. However, in the inexact case, there are restrictions on the choice of $\rho$ and $\epsilon$, for which we can guarantee the result $\mathbb {P}(F(x_k)-F^*\le \epsilon )\ge 1-\rho$.

5 Complexity Analysis: Convex Composite Objective

The following function plays a central role in our analysis:

(30)

It will be useful to establish inequalities relating H evaluated at the vector of exact updates $T_0(x)$, and H evaluated at the vector of inexact updates $T_\delta (x)$.

Lemma 5.1

For all $x\in \mathbb {R}^N$ and $\delta \in \mathbb {R}^n_+$, we have the inequalities $H(x,T_0(x)) \le H(x,T_{\delta }(x)) \le H(x,T_0(x)) + \sum _{i=1}^n \delta ^{(i)}.$

Proof

We first observe that

The rest follows by applying (13) and, subsequently, (30). $\square$

The following Lemma is a restatement of Lemma 2 in [14], which provides an upper bound on the expected distance between the current and optimal objective value in terms of the function H.

Lemma 5.2

(Lemma 2 in [14]) For $x,T \in \mathbb {R}^N$, let $x_+(x,T)$ be the random vector equal to $x + U_i T^{(i)}$ with probability $\tfrac{1}{n}$ for each $i \in \{1,2,\dots ,n\}$. Then, $\mathbb {E}[F(x_+(x,T)) - F^* \;|\; x] \le \tfrac{1}{n}(H(x,T) - F^*) + \tfrac{n-1}{n}(F(x) - F^*).$

Note that, if $x = x_k$ and $T = T_{\delta }(x_k)$, then $x_+(x,T) = x_{k+1}$, as produced by Algorithm 1. The following lemma, which provides an upper bound on H, will be used repeatedly throughout the remainder of this paper.

Lemma 5.3

For all $x \in {{\mathrm{dom}}}F$ and $\delta \in \mathbb {R}^n_+$ (letting $\varDelta = \sum _i \delta ^{(i)}$), we have $H(x,T_{\delta }(x)) \le \varDelta + \min _{y \in \mathbb {R}^N} \left\{ F(y) + \tfrac{1-\mu _f(l)}{2}\Vert y-x\Vert _{l}^2\right\} .$

We note that this result and its proof are similar in style to that of Lemma 3 in [14]. In fact, the latter result is obtained from ours by setting $\varDelta \equiv 0$.

5.1 Convex Case

Now we need to estimate $H(x,T_{\delta }(x))-F^*$ from above in terms of $F(x)-F^*$. Again, this Lemma and its proof are similar in style to that of Lemma 4 in [14].

Lemma 5.4

Fix $x^* \in X^*$, $x \in {{\mathrm{dom}}}F$, $\delta \in \mathbb {R}^n_+$ and let $R = \Vert x-x^*\Vert _{l}$ and $\varDelta =\sum _i \delta ^{(i)}$. Then,

$$\begin{aligned} H(x,T_{\delta }(x)) - F^* \le \varDelta + {\left\{ \begin{array}{ll} (1-\frac{F(x) - F^*}{2R^2})(F(x) - F^*), &{} \text {if } F(x) - F^* \le R^2,\\ \frac{1}{2}R^2 < \frac{1}{2}(F(x) - F^*), &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Proof

Strong convexity is not assumed, so $\mu _f(l) = 0$. By Lemma 5.3,

$$\begin{aligned} H(x,T_{\delta }(x))\le & {} \varDelta + \min _{y\in \mathbb {R}^N}\{ F(y) + \tfrac{1}{2} \Vert y-x\Vert _{l}^2\}\\\le & {} \varDelta +\min _{\lambda \in [0,1]} \left\{ F(\lambda x^* + (1-\lambda )x) + \tfrac{\lambda ^2}{2} \Vert x-x^*\Vert _{l}^2\right\} \\\le & {} \varDelta + \min _{\lambda \in [0,1]} \left\{ F(x) - \lambda (F(x)-F^*)+ \tfrac{\lambda ^2}{2} R^2\right\} . \end{aligned}$$

Minimizing in $\lambda$ gives $\lambda ^* = \min \{1, \frac{F(x)-F^*}{R^2} \}$ and the result follows. $\square$

Remark 5.1

Lemmas 5.3 and 5.4 generalize the results in [14]. In particular, setting $\delta ^{(i)}= 0$ for all $i = 1,\dots ,n$ in Lemmas 5.3 and 5.4 recovers Lemmas 3 and 4 in [14].

We now state the main complexity result of this section, which bounds the number of iterations sufficient for ICD, used with uniform probabilities, to decrease the value of the objective to within $\epsilon$ of the optimal value, with probability at least $1-\rho$.

Theorem 5.1

Choose an initial point $x_0\in \mathbb {R}^N$, and let $\{x_k\}_{k\ge 0}$ be the random iterates generated by ICD applied to problem (1), using uniform probabilities $p_i=\frac{1}{n}$, and inexactness parameters $\delta _k^{(1)},\dots , \delta _k^{(n)}\ge 0$, that satisfy (14) for $\alpha ,\beta \ge 0$. Let $c_1 = 2n\max \{\mathcal {R}_{l}^2(x_0),F(x_0) - F^*\}$, and $c_2 = 2n\mathcal {R}_{l}^2(x_0)/\epsilon$. Choose target confidence $0<\rho <1$, and error tolerance $\epsilon >0$, so that one of the following two conditions hold:

• (i) $\tfrac{c_1}{2}(\alpha + \sqrt{\alpha ^2 + \tfrac{4\beta }{c_1 \rho }}) < \epsilon < F(x_0) - F^*$ and $\alpha ^2 + \tfrac{4\beta }{c_1 }<1$

• (ii) $\tfrac{\beta c_2}{\rho (1-\alpha c_2)} < \epsilon < \min \{\mathcal {R}_{l}^2(x_0),F(x_0) - F^*\}$, where $\alpha c_2 < 1$.

If (i) holds and we choose K as in (16), or if (ii) holds and we choose K as in (17), then $\mathbb {P}(F(x_K)-F^* \le \epsilon ) \ge 1-\rho$.

Proof

By Lemma 4.1, $F(x_k)\le F(x_0)$ for all k, so $\Vert x_k - x^*\Vert _{l} \le \mathcal {R}_{l}(x_0)$ for all k and $x^* \in X^*$. Let $\xi _k:=F(x_k) - F^*$. Using Lemmas 5.2 and 5.4, we have

$$\begin{aligned} \mathbb {E}[\xi _{k+1} \;|\; x_k]\le & {} \bar{\delta }_k + \tfrac{1}{n} \max \left\{ 1 - \tfrac{\xi _k}{2\Vert x_k - x^*\Vert _{l}^2},\tfrac{1}{2} \right\} \xi _k + \tfrac{n-1}{n}\xi _k \nonumber \\= & {} \bar{\delta }_k + \max \left\{ 1 - \tfrac{\xi _k}{2n\Vert x_k - x^*\Vert _{l}^2},1-\tfrac{1}{2n} \right\} \xi _k \end{aligned}$$

(31)

$$\begin{aligned}\le & {} \bar{\delta }_k + \max \left\{ 1 - \tfrac{\xi _k}{2n\mathcal {R}_{l}^2(x_0)},1-\tfrac{1}{2n} \right\} \xi _k. \end{aligned}$$

(32)

(i): $\mathbb {E}[\xi _{k+1}\;|\;x_k] \le \bar{\delta }_k + \left( 1 - \xi _k / c_1 \right) \xi _k \le (1+\alpha ) \xi _k - \xi _k^2 / c_1 + \beta$ follows from (32)+(14), and the result follows by applying Theorem 4.1(i). (ii): If $\xi _k \ge \epsilon$, then $\mathbb {E}[\xi _{k+1}\;|\;x_k] \le \bar{\delta }_k + \max \left\{ 1 - \tfrac{\epsilon }{2n\mathcal {R}_{l}^2(x_0)},1-\tfrac{1}{2n} \right\} \xi _k \le \left( 1 + \alpha - 1/ c_2 \right) \xi _k + \beta$ in view of (32) + (14). The result follows by applying Theorem 4.1(ii). $\square$

5.2 Strongly Convex Case

Let us start with an auxiliary result.

Lemma 5.5

Let F be strongly convex w.r.t $\Vert \cdot \Vert _{l}$ with $\mu _f(l) + \mu _{\varPsi }(l) >0$. Then, for all $x\in {{\mathrm{dom}}}F$ and $\delta \in \mathbb {R}^n_+$, with $\varDelta = \sum _i \delta ^{(i)}$, we have $H(x,T_{\delta }(x)) - F^* \le \varDelta + \left( \tfrac{1-\mu _f(l)}{1+\mu _\varPsi (l)}\right) (F(x)-F^*)$.

Proof

Let $\mu _f = \mu _f(l)$, $\mu _\varPsi = \mu _\varPsi (l)$ and $\lambda ^* = (\mu _f + \mu _\varPsi )/(1+\mu _\varPsi ) \le 1$. Then,

where $\xi =(1-\mu _f)\lambda ^2-(\mu _f+\mu _\varPsi )\lambda (1-\lambda )$. The last inequality follows from the fact that $(\mu _f +\mu _\varPsi )(1-\lambda ^*) - (1-\mu _f)\lambda ^* = 0$. It remains to subtract $F^*$ from both sides of the final inequality. $\square$

We can now estimate the number of iterations needed to decrease a strongly convex objective F within $\epsilon$ of the optimal value with high probability.

Theorem 5.2

Let F be strongly convex with respect to the norm $\Vert \cdot \Vert _{l}$ with $\mu _f(l) + \mu _\varPsi (l)>0$ and let $\mu :=\tfrac{\mu _f(l)+\mu _\varPsi (l)}{1+\mu _\varPsi (l)}$. Choose an initial point $x_0\in \mathbb {R}^N$ and let $\{x_k\}_{k\ge 0}$ be the random iterates generated by ICD applied to problem (1), used with uniform probabilities $p_i=\tfrac{1}{n}$ for $i=1,2,\dots ,n$ and inexactness parameters $\delta _k^{(1)},\dots ,\delta _k^{(n)}\ge 0$ satisfying (14), for $0\le \alpha < \frac{\mu }{n}$ and $\beta \ge 0$. Choose confidence level $0<\rho <1$ and error tolerance $\epsilon$ satisfying $\tfrac{\beta n}{\rho (\mu -\alpha n)} <\epsilon$ and $\epsilon < F(x_0)-F^*$. Then, for K given by (17), we have $\mathbb {P}(F(x_K) - F^* \le \epsilon ) \ge 1-\rho .$

Proof

Letting $\xi _{k} = F(x_k)-F^*$, we have

$$\begin{aligned} \mathbb {E}[\xi _{k+1}\;|\; x_k]&\overset{(\text {Lemma 5.2)}}{\le } \tfrac{1}{n} (H(x_k,T_{\delta _k}(x_k)) - F^*) + \tfrac{n-1}{n}\xi _k\\&\overset{(\text {Lemma 5.5})}{\le } \bar{\delta }_k + \tfrac{1}{n}\left( \tfrac{1-\mu _f(l)}{1+\mu _\varPsi (l)} \xi _k\right) + \tfrac{n-1}{n}\xi _k \overset{(14)}{\le } \left( 1 + \alpha -\tfrac{\mu }{n}\right) \xi _k + \beta . \end{aligned}$$

By (9), $\mu \le 1$, and the result follows from Theorem 4.1(ii) with $c_2 = \frac{n}{\mu }$. $\square$

6 Complexity Analysis: Smooth Objective

In this section, we provide simplified iteration complexity results when the objective function is smooth ($\varPsi \equiv 0$ so $F \equiv f$). Furthermore, we provide complexity results for arbitrary (rather than uniform) probabilities $p_i>0$.

6.1 Convex Case

For smooth functions, we have a closed-form expression for the update:

$$\begin{aligned} T_0^{(i)}(x) \overset{(12)+(13)}{=} \arg \min _{t \in \mathbb {R}^{N_i}} \{\langle \nabla _i f(x), t \rangle + \tfrac{l_i}{2}\Vert t \Vert _{(i)}^2\} = -\tfrac{1}{l_i}B_i^{-1} \nabla _i f(x). \end{aligned}$$

(33)

Substituting this into $V_i(x,\cdot )$ yields

$$\begin{aligned} V_i(x,T_0^{(i)}(x)) =\langle \nabla _i f(x),T_0^{(i)}(x) \rangle + \tfrac{l_i}{2}\Vert T_0^{(i)}(x) \Vert _{(i)}^2 = -\tfrac{1}{2l_i}(\Vert \nabla _i f(x)\Vert _{(i)}^*)^2. \end{aligned}$$

(34)

We can now estimate the decrease in f during one iteration of ICD:

$$\begin{aligned} f(x + U_i T_{\delta }^{(i)}(x)) - f(x)\overset{(4)}{\le } \langle \nabla _i f(x), T_{\delta }^{(i)}(x) \rangle + \tfrac{l_i}{2}\Vert T_{\delta }^{(i)}(x)\Vert _{(i)}^2 \overset{(12)}{=} V_i(x,T_\delta ^{(i)}(x)) \nonumber \\ \overset{(13)}{\le } \min \{0,\delta ^{(i)} + V_i(x,T_0^{(i)}(x))\} \overset{(34)}{=} \min \{0,\delta ^{(i)} - \tfrac{1}{2l_i}\big (\Vert \nabla _i f(x)\Vert _{(i)}^*\big )^2\}.\nonumber \\ \end{aligned}$$

(35)

The main iteration complexity result of this section can now be established.

Theorem 6.1

Choose an initial point $x_0\in \mathbb {R}^N$ and let $\{x_k\}_{k\ge 0}$ be the random iterates generated by ICD applied to the problem of minimizing f, used with probabilities $p_1,\dots ,p_n >0$ and inexactness parameters $\delta _k^{(1)},\dots , \delta _k^{(n)}\ge 0$ satisfying (14) for $\alpha ,\beta \ge 0$, where $\alpha ^2 +\tfrac{4\beta }{c_1}<1$ and $c_1 =2\mathcal {R}_{lp^{-1}}^2(x_0)$. Choose confidence level $0<\rho <1$, error tolerance $\epsilon$ satisfying $\tfrac{c_1}{2}(\alpha + \sqrt{\alpha ^2 + \tfrac{4\beta }{c_1 \rho }}) < \epsilon$ and $\epsilon < f(x_0)-f^*$, and let the iteration counter K be given by (16). Then, $\mathbb {P}(f(x_K) - f^* \le \epsilon ) \ge 1-\rho .$

Proof

We first estimate the expected decrease of the objective function during one iteration of the method:

$$\begin{aligned} \textstyle \mathbb {E}[f(x_{k+1})\;|\;x_k]= & {} \textstyle f(x_k) +\sum _{i=1}^n p_i [f(x_k+U_i T_{\delta _k}^{(i)}(x_k)) - f(x_k)]\nonumber \\&\overset{(35)}{\le } \textstyle f(x_k) + \sum _{i=1}^n p_i \left( \delta _k^{(i)} - \tfrac{1}{2l_i}\big (\Vert \nabla _i f(x_k)\Vert _{(i)}^*\big )^2\right) \nonumber \\&\overset{(6)}{=} \textstyle f(x_k) - \tfrac{1}{2}\big (\Vert \nabla f(x_k)\Vert _{lp^{-1}}^*\big )^2 + \sum _{i=1}^n p_i \delta _k^{(i)}\nonumber \\\le & {} f(x_k) - \tfrac{1}{2} \big (\Vert \nabla f(x_k)\Vert _{lp^{-1}}^*\big )^2 + \alpha (f(x_k)-f^*) + \beta . \end{aligned}$$

(36)

Note that $f(x_k)-f^*\le \max _{x^* \in X^*} \langle \nabla f(x_k) , x_k - x^*\rangle \le \Vert \nabla f(x_k)\Vert _{lp^{-1}}^* \mathcal {R}_{lp^{-1}}(x_0)$ because $f(x_k) \le f(x_0)$ $\forall k$. Substituting the previous into (36), we obtain $\mathbb {E}[f(x_{k+1})-f^*\;|\;x_k] \le f(x_k) - f^* - \tfrac{1}{2} \left( \tfrac{f(x_k) - f^*}{\mathcal {R}_{lp^{-1}}(x_0)}\right) ^2 + \alpha (f(x_k)-f^*) + \beta .$ It remains to apply Theorem 4.1(i). $\square$

6.2 Strongly Convex Case

In this section, we assume that f is strongly convex with respect to $\Vert \cdot \Vert _{lp^{-1}}$ with convexity parameter $\mu _f(lp^{-1})$. Using (7) with $x = x_k$ and $y = x^*$, and letting $h = x^*-x_k$, we obtain $f^* - f(x_k) \ge \langle \nabla f(x_k),h\rangle + \tfrac{\mu _f(lp^{-1})}{2}\Vert h\Vert _{lp^{-1}}^2 .$ By minimizing the right-hand side in h, we get

$$\begin{aligned} f(x_k)-f^* \le \tfrac{1}{2\mu _f(lp^{-1})}(\Vert \nabla f(x_k)\Vert _{lp^{-1}}^*)^2. \end{aligned}$$

(37)

We can now give an efficiency estimate for strongly convex objectives.

Theorem 6.2

Let f be strongly convex with respect to the norm $\Vert \cdot \Vert _{lp^{-1}}$, with convexity parameter $\mu _f(lp^{-1})>0$. Choose an initial point $x_0\in \mathbb {R}^N$, and let $\{x_k\}_{k\ge 0}$ be the random iterates generated by ICD, applied to the problem of minimizing f, used with probabilities $p_1,\dots ,p_n>0$, and inexactness parameters $\delta _k^{(1)},\dots , \delta _k^{(n)}\ge 0$, that satisfy (14) for $0\le \alpha < \mu _f(lp^{-1})$ and $\beta \ge 0$. Choose the confidence level $0<\rho <1$, let the error tolerance $\epsilon$ satisfy $\frac{\beta }{\rho (\mu _f(lp^{-1}) - \alpha )} < \epsilon < f(x_0)-f^*$, let $c_2 = 1/\mu _f(lp^{-1})$, and let iteration counter K be as in (17). Then, $\mathbb {P}(f(x_K) - f^* \le \epsilon ) \ge 1- \rho .$

Proof

The expected decrease of the objective function during one iteration of the method can be estimated as follows:

$$\begin{aligned} \mathbb {E}[f(x_{k+1}) - f^*|x_k]&\overset{(36)}{\le } (1+\alpha )(f(x_k) -f^*) - \tfrac{1}{2}(\Vert \nabla f(x_k)\Vert _{lp^{-1}}^*)^2 + \beta \\&\overset{(37)}{\le } (1+\alpha - \mu _f(lp^{-1}))(f(x_k) -f^*) + \beta . \end{aligned}$$

It remains to apply Theorem 4.1(ii) with $\varphi (x_k) = f(x_k) - f^*$. $\square$

7 Practical Aspects of an Inexact Update

In this section, the goal is to demonstrate the practical importance of employing an inexact update in the (block) CD method.

First, we remind the reader that, unless the block size is $N_i=1$, a closed-form expression for the update subproblem may not exist, so inexact updates provide a mechanism for overcoming this exact solvability issue. Furthermore, even if closed-form solutions do exist, such as for standard least squares or ridge-regression problems, it is not always computationally efficient to solve the subproblems exactly via a direct method. (See our computational experiments in Sect. 8.) We have also remarked that inexact updates allow iterative methods to be used to solve the update subproblem, so ICD extends the range of tools that can be used to tackle problems of the form (1).

Moreover, if the block size is $N_i=1$, then only the diagonal of the Hessian (of f) is taken into account, via the Lipschitz constants $L_i$ (and $B_i$ is a scalar.) However, if the Hessian is not well approximated by a diagonal matrix (i.e., if the problem is ill-conditioned), then coordinate descent methods can struggle and converge slowly. Therefore, if the block size is $N_i>1$, blocks of the Hessian can be incorporated via the matrix $B_i$, and even this small amount of curvature information can be very beneficial for ill-conditioned problems.

7.1 Solving Smooth Problems via ICD

Here, we assume that $\varPsi =0$, so the function $F(x) = f(x)$ is smooth and convex. Then, the overapproximation is

$$\begin{aligned} f(x_k+U_i t) \overset{(4)+ (3)}{\le } f(x_k) + \langle \nabla _i f(x_k), t\rangle + \tfrac{l_i}{2}\langle B_i t , t\rangle \equiv f(x_k) + V_i(x_k,t). \end{aligned}$$

(38)

By minimizing the right-hand side in (38) in t, we see that determining the update to block i at iteration k is equivalent to solving the system of equations

$$\begin{aligned} B_i t = - \tfrac{1}{l_i} \nabla _i f(x_k). \end{aligned}$$

(39)

Clearly, solving systems of equations is central to the block coordinate descent method in the smooth case.

Exact CD [9] requires the exact update (39), which depends on the inverse of an $N_i \times N_i$ matrix. A standard approach to solving for $t=T_0^{(i)}(x_k)$ in (39) is to form the Cholesky factors of $B_i$, followed by two triangular solves. This can be extremely expensive for medium $N_i$, or dense $B_i$.

Because $B_i$ is positive definite, a natural choice is to solve (38) using conjugate gradients (CG) [34]. (This is the method we adopt in the numerical experiments presented in Sect. 8.) It is widely accepted that using an iterative technique has many advantages over a direct method for solving systems of equations, so we expect that an inexact update can be determined quickly, and subsequently the overall ICD algorithm running time reduces. Moreover, applying a preconditioner to (38) can enable even faster convergence of CG. Finding good preconditioners is an active area of research; see, e.g., [35–37].

Quadratic. Consider now unconstrained quadratic minimization

$$\begin{aligned} \min _{x \in \mathbb {R}^N} f(x) = \tfrac{1}{2} \Vert A x - b\Vert _2^2, \end{aligned}$$

(40)

where $A \in \mathbb {R}^{M \times N}$, and $b \in \mathbb {R}^M$. In this case, (4) becomes

$$\begin{aligned} f(x + U_it) = \tfrac{1}{2}\Vert A(x+U_it) - b\Vert _2^2 = f(x) + \langle \nabla _i f(x) ,t \rangle + \tfrac{1}{2}\langle A_i^TA_it ,t \rangle , \end{aligned}$$

(41)

where $A_i = U_i A$. Comparing (41) with (38), we see that in the quadratic case, (41) is an exact upper bound on $f(x + U_it)$ if we choose $l_i = 1$ and $B_i = A_i^TA_i$ for all blocks i . The matrix $B_i$ must be positive definite, so $A_i$ is assumed to have full (column) rank.¹ Substituting $l_i = 1$ and $B_i = A_i^TA_i$ into (39) gives

$$\begin{aligned} A_i^TA_i t = - A_i^T(Ax-b). \end{aligned}$$

(42)

Therefore, when ICD is applied to a problem of the form (40), the update is found by inexactly solving (42).

7.2 Solving Non-smooth Problems via ICD

The non-smooth case is not as simple as the smooth case, because the update subproblem will have a different form for each non-smooth term $\varPsi$. However, we will see that in many cases, the subproblem will have the same, or similar, form to the original objective function. We demonstrate this through the use of the following concrete examples.

Group Lasso. A widely studied optimization problem arising in statistical learning is the group lasso problem, which has the form

$$\begin{aligned} \textstyle \min _{x \in \mathbb {R}^N} \tfrac{1}{2}\Vert Ax-b\Vert _2^2 + \lambda \sum \limits _{i=1}^n \sqrt{d_i} \Vert x^{(i)}\Vert _2, \end{aligned}$$

(43)

where $\lambda >0$ is a regularization parameter and $d_i$, for all i, is a weighting parameter that depends on the size of the ith block. Formulation (43) fits the structure (1) with $f(x) = \tfrac{1}{2} \Vert Ax-b\Vert _2^2$ and $\varPsi (x) = \sum _{i=1}^n \lambda \sqrt{d_i} \Vert x^{(i)}\Vert _2$. If we choose $B_i = A_i^TA_i$ (assuming $A_i^TA_i\succ 0$), then $l_i = 1$ for all i. Letting $r_k=b-A x_k$, we have

$$\begin{aligned} V_i(x_k,t)= & {} \langle \nabla _i f(x_k) , t \rangle + \tfrac{1}{2}\langle B_i t , t\rangle + \lambda \sqrt{d_i}\Vert x^{(i)}+t\Vert _2 \\= & {} \tfrac{1}{2}\Vert A_i t -r_k\Vert _2^2 - \tfrac{1}{2}\Vert r_k\Vert _2^2 + \lambda \sqrt{d_i}\Vert x^{(i)}+t\Vert _2. \end{aligned}$$

Note that

$$\begin{aligned} T_0^{(i)}= \arg \min _{t\in \mathbb {R}^{N_i}} V_i(x_k,t) = \arg \min _t \tfrac{1}{2}\Vert A_it-r_k\Vert _2^2 + \lambda \sqrt{d_i} \Vert x_k^{(i)}+t\Vert _2. \end{aligned}$$

(44)

We see that (44) has the same form as the original problem (43), but is of a smaller dimension ($N_i$ as opposed to N). One can apply any algorithm to approximately minimize (44). Our theory would hold if the method uses one of the stopping conditions described in Sect. 4.4.

8 Numerical Experiments

In this section, we present numerical results to demonstrate the practical performance of Inexact Coordinate Descent and compare the results with Exact Coordinate Descent. We note that a thorough practical investigation of Exact CD is given in [14], where its usefulness on huge-scale problems is evidenced. We do not intend to reproduce such results for ICD; rather, we investigate the affect of inexact updates compared with exact updates, which should be apparent on medium-scale problems. We do this the full knowledge that, if Exact CD scales well to very large sizes (shown in [14]), then so too will ICD.

Each experiment presented in this section was implemented in Matlab and run (under Linux) on a desktop computer with a Quad Core i5-3470CPU, 3.20GHz processor with 24GB of RAM.

8.1 Problem Description for a Smooth Objective

In this numerical experiment, we assume that the function $F =f$ is quadratic (40) and $\varPsi = 0$. Furthermore, as ICD can work with blocks of data, we impose block structure on the system matrix. In particular, we assume that the matrix A has block angular structure. Matrices with this structure frequently arise in optimization, from optimal control, scheduling and planning problems to stochastic optimization problems, and exploiting this structure is an active area of research [38–40]. To this end, we define

(45)

where $A \in \mathbb {R}^{M \times N}$, $C \in \mathbb {R}^{m \times N}$, $D \in \mathbb {R}^{\ell \times N}$, and $A_i \in \mathbb {R}^{M \times N_i}$. Moreover, we assume that each block $C_i \in \mathbb {R}^{M_i \times N_i}$, and the linking blocks $D_i\in \mathbb {R}^{\ell \times N_i}$. We assume that $\ell \ll N$ and that there are n blocks with $m = \sum _{i=1}^n M_i$, so $M = m + \ell$, and $N = \sum _{i=1}^n N_i$.

If $D = \mathbf {0}$, where $\mathbf {0}$ is the $\ell \times N$ zero matrix, then problem (40) is completely (block) separable, so it can be solved easily. The linking constraints D make problem (40) non-separable, so it is non-trivial to solve.

The system of equations (42) must be solved at each iteration of ICD (where $B_i = A_i^TA_i= C_i^TC_i+ D_i^TD_i$) because it determines the update to apply to the ith block. We solve this system inexactly using an iterative method. In particular, we use the conjugate gradient method (CG) in the numerical experiments presented in this section.

It is well known that the performance of CG is improved by the use of an appropriate preconditioner. To this end, we compare ICD using CG with ICD using preconditioned CG (PCG). If $M_i \ge N_i$ and rank($C_i) = N_i$, then the block $C_i^TC_i$ is positive definite, so we propose the preconditioner

$$\begin{aligned} \mathcal {P}_i:=C_i^TC_i\end{aligned}$$

(46)

(for the ith system). If $M_i< N_i$ then $\mathcal {P}_i$ is rank deficient and is therefore singular. In such a case, we perturb (46) by adding a multiple of the identity matrix and propose the non-singular preconditioner (with $\rho > 0$)

$$\begin{aligned} \hat{\mathcal {P}_i} = \mathcal {P}_i+ \rho I = C_i^TC_i+ \rho I. \end{aligned}$$

(47)

Applying the preconditioners (46) for $M_i\ge N_i$, and (47) for $M_i<N_i$, to (42), should result in the system having better spectral properties than the original, leading to faster convergence of the CG method.

Remark 8.1

The preconditioners (46) and (47) are likely to be significantly more sparse than $B_i$, and consequently we expect that these preconditioners will be cost-effective to apply in practice. To see this, note that the blocks $C_i$ are generally much sparser than the linking blocks $D_i$ so that $\mathcal {P}_i= C_i^TC_i$ is much sparser than $C_i^TC_i+D_i^TD_i$.

Experimental Parameters and Results. We now study the use of an iterative technique (CG or PCG) to determine the update used at each iteration of ICD and compare this approach with Exact CD. For Exact CD, the system (42) was solved by forming the Cholesky decomposition of $B_i$ for each i and then performing two triangular solves to find the exact update.²

In the first two experiments, simulated data were used to generate A and the solution vector $x_*$. For each matrix A, each block $C_i$ has approximately 20 nonzeros per column, and the density of the linking constraints $D_i$ is approximately $0.1\,\ell \,N_i$. The data vector b was generated from $b=Ax_*$, so the optimal value is known in advance: $F^* = 0$. The stopping condition and tolerance $\epsilon$ for ICD are: $F(x_K) -F^* = \tfrac{1}{2}\Vert Ax_K-b\Vert _2^2 < \epsilon = 0.1$.

The inexactness parameters are set to $\alpha = 0$ and $\beta = 0.1$. Moreover, each block was chosen with uniform probability $\frac{1}{n}$ in all experiments in this section.

In the first experiment, the blocks $C_i$ are tall, so the preconditioner $\mathcal {P}_i$ was used. In the second experiment, the blocks $C_i$ are wide, so the perturbed preconditioner $\hat{\mathcal {P}}_i= \mathcal {P}_i+\rho I$ (with $\rho = 0.5$) was used.³ For both preconditioners, the incomplete Cholesky decomposition was found using Matlab’s ‘ichol’ function with a drop tolerance set to 0.1. The results are given in Table 3, and all results are averaged over 20 runs.⁴

The terminology used in the tables is as follows. ‘Time’ represents the total CPU time in seconds from, and including, algorithm initialization, until algorithm termination. (For Exact CD, this includes the time needed to compute the Cholesky factors of $B_i$ once for each $i=1,\dots ,n$. For the inexact versions, this includes the time needed to form the preconditioners.) Furthermore, the term ‘block updates’ refers to the total number of block updates computed throughout the algorithm; dividing this number by n gives the number of ‘epochs,’ which is (approximately) equivalent to the total number of full-dimensional matrix–vector products required by the algorithm. The abbreviation ‘o.o.m.’ is the out of memory token.

In Table 2, we present a list of the parameters used in the numerical experiments. The results of the numerical experiments are presented in Table 3.

Table 2 Problem parameters used in the experiments, whose results are given in Table 3

Table 3 Results of Exact CD, and ICD with CG or PCG applied to (40) with structure (45) using simulated data

The results presented in Table 3 show that ICD with either CG or PCG outperforms Exact CD in terms of CPU time. When the blocks are of size $M_i \times N_i = 10^4 \times 10^3$, ICD is approximately 3 times faster than Exact CD. The results are even more striking as the block size increases. ICD was able to solve problems of all sizes, whereas Exact CD ran out of memory on the problems of size $10^7 \times 10^6$. Furthermore, PCG is faster than CG in terms of CPU time, demonstrating the benefits of preconditioning. These results strongly support the ICD method. For problems with wide blocks (10–15), ICD is able to solve all problem instances, whereas Exact CD gives the out of memory token on the large problems. When $\ell$ is small, ICD with PCG has an advantage over ICD with CG. However, when $\ell$ is large, the preconditioner $\hat{\mathcal {P}}_i$ is not as good an approximation to $A_i^TA_i$, and so ICD with CG is preferable.

Remark 8.2

Here, we remark on the numerical experiments.

• 1. For problems 7–9 and 13–15, Exact CD was out of memory. Exact CD requires the matrices $B_i = C_i^TC_i + D_i^TD_i$ for all i to be formed explicitly, and the Cholesky factors to be found and stored. Even if $A_i$ is sparse, $B_i$ need not be, and the Cholesky factor could be dense, making it very expensive to work with. Moreover, this problem does not arise for ICD with CG (and arises to a much lesser extent for PCG) because $B_i$ is never explicitly formed. Instead, only sparse matrix–vector products of the form $B_ix \equiv C_i^T(C_i x) + D_i^T(D_i x)$ are required. This is why ICD performs extremely well, even when the blocks are very large.

• 2. We note that, to avoid the o.o.m. token for Exact CD, instead of forming and storing all the Cholesky factors when initializing the algorithm, one could simply compute the Cholesky factor for each block as needed on the fly and then discard it. (However, this comes with a much increased computational cost).

Experiments with Real-World Data. Here, we test ICD on a quadratic objective (40) with the structure (45), where the matrices arise from real-world applications. In particular, we have taken several matrices from the Florida Sparse Matrix Collection [41] that have block angular structure (see Table 4). We have taken the transpose of the original matrix to ensure that the matrix is tall. Furthermore, in each case the upper block (recall (45)) is diagonal, so we have scaled each of the matrices so that $C = I$. Note that, in this case, $\mathcal {P}_i= I$ so there is no need for preconditioning. We compare Exact CD with ICD using CG. All the stopping conditions and algorithm parameters are as described earlier in this section.

Table 4 Block angular matrices from the Florida Sparse Matrix Collection [41]

The results for these matrices are given in Table 5. To determine n and $N_i$, we have simply taken the prime factorization of N. ICD with CG performs extremely well on these test problems. In most cases, ICD with CG needs more iterations than Exact CD to converge, yet ICD requires only a fraction of the CPU time needed by Exact CD.

Table 5 Exact CD and ICD with CG applied to a quadratic function with the block angular matrices described in Table 4

8.2 A Numerical Experiment for a Non-smooth Objective

Here, we consider the $l_1$-regularized least squares problem

$$\begin{aligned} \min _{x\in \mathbb {R}^N} \tfrac{1}{2} \Vert Ax - b\Vert _2^2 + \lambda \Vert x\Vert _1, \end{aligned}$$

(48)

where $A \in \mathbb {R}^{M \times N}$, $b \in \mathbb {R}^M$ and $\lambda >0$. Problem (48) fits into the framework (1) with $f(x) = \frac{1}{2} \Vert Ax - b\Vert _2^2$ and $\varPsi (x)= \lambda \Vert x\Vert _1 = \lambda \sum _{i=1}^n \Vert x^{(i)}\Vert _1$. The matrix A is sparse, with approximately 20 nonzeros per column. (We also ensure that each $A_i$ has full rank by adding an identity matrix padded with zeros to each block $A_i$.) We set $B_i = A_i^TA_i$ and $l_i = 1$ $\forall i$. (By construction $B_i$ is positive definite and it can be shown that this choice of $B_i$ and $l_i$ satisfies the overapproximation (4).) Further, for this experiment we use uniform probabilities, $p_i = \frac{1}{n}$ for all i, and we set $\alpha = 0$ and $\beta > 0$. The algorithm stopping condition is $F(x_k)-F^*< \epsilon = 10^{-4}$ (the data were constructed so that $F^*$ is known), and the regularization parameter was set to $\lambda = 0.01$.

The exact update for the ith block is computed via

$$\begin{aligned}&T_{0}^{(i)}\overset{(12)}{=} \arg \min _t \; -\langle A_i^Tr_k, t\rangle + \tfrac{1}{2}t^TA_i^TA_i t + \lambda \Vert x_k^{(i)}+ t\Vert _1\nonumber \\&\quad = \arg \min _t\tfrac{1}{2} \Vert A_it - r_k\Vert _2^2 - \tfrac{1}{2}\Vert r_k\Vert _2^2+ \lambda \Vert x_k^{(i)}+ t\Vert _1, \end{aligned}$$

(49)

where $r_k :=b-Ax_k$ and $\nabla _i f(x) = -A_i^Tr_k$. As long as $N_i>1$, (49) does not have a closed-form solution, which means that only an inexact update can be used in this case. Recall that the inexact update must satisfy (13), and for (49), we do not know the optimal value $V_i(x_k,T_0^{(i)})$. So, to ensure that (13) is satisfied, we simply find the inexact update using any algorithm that terminates on the duality gap. In particular, we use the BCGP algorithm [42] to solve for the update at each iteration of ICD. The BCGP algorithm is a gradient-based method that solves problems of the form (49) and terminates on the duality gap. (Condition (19) in [43] is used to compute the duality gap.) That is, we accept $T_{\delta _k}^{(i)}$ using a stopping condition of the same form as that given by (15).

We conduct two numerical experiments. In the first experiment, A is of size $0.5N \times N$, where $N = 10^5$. In this case (48) is convex (but not strongly convex.) This means that the complexity result of Theorem 5.1 applies. In the second experiment, A is of size $2N \times N$, where $N = 10^5$. In this case (48) is strongly convex, and Theorem 5.2 applies.

The purpose of these experiments is to investigate the effect of different levels of inexactness (different values of $\beta$) on the algorithm runtime. In particular, we used three different values: $\beta \in \{10^{-4},10^{-6},10^{-8}\}$. To make this a fair test, for each problem instance, the block ordering was fixed in advance. (i.e., before the algorithm begins, we form and store a vector whose kth element is a index between 1 and n that has been chosen with uniform probability, corresponding to the block to be updated at iteration k of ICD.) Then, ICD was run three times using this block ordering, once for each value of $\beta \in \{10^{-4},10^{-6},10^{-8}\}$. In all cases we use $\delta _k^{(i)}= \beta$ for all i and k. Figure 1 shows the results of experiments 1 ($M < N$) and 2 ($M > N$), respectively. The experiments were performed many times on simulated data, and the plots shown are a particular instance, which is representative of the typical behavior observed using ICD on this problem description. We see that when the same block ordering is used, all algorithms essentially require the same number of iterations until termination regardless of the parameter $\beta$, which is to be expected. The curves overlap in the first and third plots, showing that changing that value of $\beta$ does not affect the number of iterations needed by the algorithm. On the other hand, clearly, using a smaller value of $\beta$, corresponding to more ‘inexactness’ in the computed update, leads to a reduction in the algorithm running time, without affecting the ultimate convergence of ICD. This shows that using an inexact update (an iterative method) has significant practical advantages.

Fig. 1

Plots of the objective function value vs the number of iterations and cputime for problem (48). Left 2 plots: A is $0.5N \times N$. Right 2 plots: A is $2N \times N$. In all cases $N = 10^5$, $n = 10$ and $N_i = 10^4$ for all $i=1,\dots ,n$

9 Conclusions

In this paper, we have presented a new randomized coordinate descent method, which can be applied to convex composite problems of the form (1), which allows the update subproblems to be solved inexactly. We call this algorithm, the Inexact Coordinate Descent (ICD) method. We have analyzed ICD and have developed a complete convergence theory for it. In particular, we have presented iteration complexity results, which give the number of iterations needed by ICD to obtain an $\epsilon$-accurate solution, with high probability. Some of the benefits of inexact updates include: (1) a wider range of problems can be solved using inexact updates (because not all problems have a closed-form solution); (2) the user has greater flexibility in solving the subproblems, because iterative methods can be used; and (3) inexact updates are often cheaper and faster to obtain than exact updates, so the overall algorithm running time is reduced. Moreover, we have presented several numerical experiments to demonstrate the practical advantages of employing inexact updates.