Skip to main content
SpringerLink
Log in

A Primal–Dual Splitting Method for Convex Optimization Involving Lipschitzian, Proximable and Linear Composite Terms

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

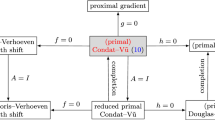
We propose a new first-order splitting algorithm for solving jointly the primal and dual formulations of large-scale convex minimization problems involving the sum of a smooth function with Lipschitzian gradient, a nonsmooth proximable function, and linear composite functions. This is a full splitting approach, in the sense that the gradient and the linear operators involved are applied explicitly without any inversion, while the nonsmooth functions are processed individually via their proximity operators. This work brings together and notably extends several classical splitting schemes, like the forward–backward and Douglas–Rachford methods, as well as the recent primal–dual method of Chambolle and Pock designed for problems with linear composite terms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Sidky, E.Y., Jørgensen, J.H., Pan, X.: Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle–Pock algorithm. Phys. Med. Biol. 57(10), 3065–3091 (2012)

    Article  Google Scholar 

  2. Mercier, B.: Topics in Finite Element Solution of Elliptic Problems. Lectures on Mathematics, vol. 63. Tata Institute of Fundamental Research, Bombay (1979)

    MATH  Google Scholar 

  3. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  4. Passty, G.B.: Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 72, 383–390 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  5. Eckstein, J.: Splitting methods for monotone operators with applications to parallel optimization. Ph.D. Thesis, MIT, Cambridge, MA (1989)

  6. Eckstein, J., Bertsekas, D.P.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55, 293–318 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  7. Combettes, P.: Solving monotone inclusions via compositions of nonexpansive averaged operators. Optimization 53(5–6), 475–504 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  8. Moreau, J.J.: Fonctions convexes duales et points proximaux dans un espace hilbertien. C. R. Math. Acad. Sci. 255, 2897–2899 (1962)

    MathSciNet  MATH  Google Scholar 

  9. Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. In: Bauschke, H.H., Burachik, R., Combettes, P.L., Elser, V., Luke, D.R., Wolkowicz, H. (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer, New York (2010)

    Google Scholar 

  10. Goldstein, T., Osher, S.: The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2(2), 323–343 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chambolle, A., Caselles, V., Cremers, D., Novaga, M., Pock, T.: An introduction to total variation for image analysis. In: Theoretical Foundations and Numerical Methods for Sparse Recovery. Radon Series Comp. Appl. Math, vol. 9, pp. 263–340. de Gruyter, Berlin (2010)

    Google Scholar 

  12. Becker, S., Candès, E., Grant, M.: Templates for convex cone problems with applications to sparse signal recovery. Math. Program. Comput. 3(3), 165–218 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  13. Monteiro, R.D.C., Svaiter, B.F.: Iteration-complexity of block-decomposition algorithms and the alternating minimization augmented Lagrangian method (2010). Preprint, submitted to Math. Program.

  14. Chambolle, A., Pock, T.: A first-order primal–dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  15. Esser, E., Zhang, X., Chan, T.: A general framework for a class of first order primal–dual algorithms for convex optimization in imaging science. SIAM J. Imaging Sci. 3(4), 1015–1046 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. Zhang, X., Burger, M., Osher, S.: A unified primal-dual algorithm framework based on Bregman iteration. J. Sci. Comput. 46(1), 20–46 (2010)

    Article  MathSciNet  Google Scholar 

  17. He, B.S., Yuan, X.M.: Convergence analysis of primal–dual algorithms for a saddle-point problem: from contraction perspective. SIAM J. Imaging Sci. 5, 119–149 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. Pesquet, J.C., Pustelnik, N.: A parallel inertial proximal optimization method. Pac. J. Optim. 8(2), 273–305 (2012)

    MathSciNet  MATH  Google Scholar 

  19. Briceño-Arias, L.M., Combettes, P.L.: A monotone + skew splitting model for composite monotone inclusions in duality. SIAM J. Optim. 21(4), 1230–1250 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Combettes, P.L., Dũng, D., Vũ, B.C.: Proximity for sums of composite functions. J. Math. Anal. Appl. 380(2), 680–688 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  21. Combettes, P.L., Pesquet, J.C.: Primal–dual splitting algorithm for solving inclusions with mixtures of composite, Lipschitzian, and parallel-sum type monotone operators. Set-Valued Var. Anal. 20(2), 307–330 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  22. Svaiter, B.F.: On weak convergence of the Douglas–Rachford method. SIAM J. Control Optim. 49(1), 280–287 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  23. Raguet, H., Fadili, J., Peyré, G.: Generalized forward–backward splitting (2011). Preprint. arXiv:1108.4404

  24. Vũ, B.C.: A splitting algorithm for dual monotone inclusions involving cocoercive operators. Adv. Comput. Math. (2011, to appear). Preprint. arXiv:1110.1697. doi:10.1007/s10444-011-9254-8

  25. Gabay, D.: Applications of the method of multipliers to variational inequalities. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary-Value Problems, Amsterdam, Netherlands (1983)

    Google Scholar 

  26. Tseng, P.: Applications of splitting algorithm to decomposition in convex programming and variational inequalities. SIAM J. Control Optim. 29, 119–138 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  27. Chen, H.G.: Forward–backward splitting techniques: theory and applications. Ph.D. Thesis, University of Washington, Seattle, WA (1994)

  28. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  29. Rockafellar, R.T.: Conjugate Duality and Optimization. SIAM, Philadelphia (1974)

    Book  MATH  Google Scholar 

  30. Robinson, S.M.: Composition duality and maximal monotonicity. Math. Program. 85, 1–13 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  31. Pennanen, T.: Dualization of generalized equations of maximal monotone type. SIAM J. Optim. 10, 809–835 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  32. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2011)

    Book  MATH  Google Scholar 

  33. Rockafellar, R.T.: Minimax theorems and conjugate saddle-functions. Math. Scand. 14, 151–173 (1964)

    MathSciNet  MATH  Google Scholar 

  34. McLinden, L.: An extension of Fenchel’s duality theorem to saddle functions and dual minimax problems. Pac. J. Math. 50, 135–158 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  35. Chaux, C., Pesquet, J.C., Pustelnik, N.: Nested iterative algorithms for convex constrained image recovery problems. SIAM J. Imaging Sci. 2(2), 730–762 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  36. Dupé, F.X., Fadili, M.J., Starck, J.L.: A proximal iteration for deconvolving Poisson noisy images using sparse representations. IEEE Trans. Image Process. 18(2), 310–321 (2009)

    Article  MathSciNet  Google Scholar 

  37. Fadili, J.M., Peyré, G.: Total variation projection with first order schemes. IEEE Trans. Image Process. 20(3), 657–669 (2011)

    Article  MathSciNet  Google Scholar 

  38. Chen, G., Teboulle, M.: A proximal-based decomposition method for convex minimization problems. Math. Program. 64, 81–101 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  39. Ogura, N., Yamada, I.: Non-strictly convex minimization over the fixed point set of an asymptotically shrinking nonexpansive mapping. Numer. Funct. Anal. Optim. 23(1–2), 113–137 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  40. Polyak, B.T.: Introduction to Optimization. Optimization Software, Inc., Publications Division, New York, USA (1987)

Download references

Acknowledgements

This work has been done at the author’s previous affiliation, the GREYC research center in Caen, France. The author wants to thank Jalal Fadili and Jean-Christophe Pesquet for stimulating discussions around splitting. He also thanks Isao Yamada for pointing out his article [39], which allowed to improve Lemma 4.3 in comparison with the result derived in a previous version of this manuscript. Moreover, the author is grateful to the anonymous referees and the associate editor for their valuable comments, which have contributed to the final preparation of the paper.

Author information

Authors and Affiliations

  1. GIPSA-Lab, CNRS—Grenoble Institute of Technology, 11 rue des Mathématiques, Campus BP46, 38402, St. Martin d’Hères Cedex, France

    Laurent Condat

Authors
  1. Laurent Condat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Laurent Condat.

Additional information

Communicated by Alexander S. Strekalovsky.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Condat, L. A Primal–Dual Splitting Method for Convex Optimization Involving Lipschitzian, Proximable and Linear Composite Terms. J Optim Theory Appl 158, 460–479 (2013). https://doi.org/10.1007/s10957-012-0245-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-012-0245-9

Keywords

Search

Navigation