1 Introduction

The search for therapy approaches that would avoid drug resistance is of tantamount importance in medicine. Two approaches that are currently being pursued in their experimental stages are immunotherapy and anti-angiogenic treatments. Immunotherapy tries to coax the body’s immune system to take action against the cancerous growth. Tumor anti-angiogenesis is a cancer therapy approach that targets the vasculature of a growing tumor. Contrary to traditional chemotherapy, anti-angiogenic treatment does not target the quickly duplicating and genetically unstable cancer cells, but instead the genetically stable normal cells. It was observed in experimental cancer that there is no resistance to the angiogenic inhibitors [1]. For this reason, tumor anti-angiogenesis has been called a therapy “resistant to resistance” that provides a new hope for the treatment of tumor-type cancers [2]. In the last 15 years, tumor anti-angiogenesis became an active area of research not only in medicine [3, 4], but also in mathematical biology [5–7], and several models of dynamics of angiogenesis have been described, e.g., by Hahnfeldt et al. [5] and d’Onofrio [6, 7]. In a sequence of papers [8–11], Ledzewicz and Schaettler completely described and solved corresponding to them, optimal control problems from a geometrical optimal control theory point of view. In most of the mentioned papers, the numerical calculations of approximate solutions are presented. However, in none of them are proved assertions that calculated numerical solutions that are really near the optimal one. The aim of this paper is an analysis of the optimal control problem from the Hamilton–Jacobi–Bellman point of view, i.e., using a dynamic programming approach, and to prove that, for calculated numerically solutions the functional considered takes an approximate value with a given accuracy.

2 Formulation of the Problem

In the paper, the following free terminal time T problem

$$ \text{(P):}\quad \mbox{minimize}\ J(p,q,u):=p(T)+\kappa \int_{0}^{T}u(t)\,dt $$
(1)

over all Lebesgue measurable functions u:[0,T]→[0,a]=U that satisfy a constraint on the total amount of anti-angiogenic inhibitors to be administered

$$ \int_{0}^{T}u(t)\,dt\leq A, $$
(2)

subject to

(3)
(4)

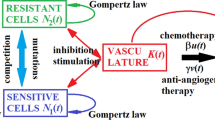
is investigated. The term \(\int_{0}^{T}u(t)\,dt\) is viewed as a measure for the cost of the treatment or related to side effects. The upper limit a in the definition of the control set U=[0,a] is a maximum dose at which inhibitors can be given. Note that the time T does not correspond to a therapy period. However, instead the functional (1) attempts to balance the effectiveness of the treatment with cost and side effects through the positive weight κ at this integral. The state variables p and q are, respectively, the primary tumor volume and the carrying capacity of the vasculature. Tumor growth is modelled by a Gompertzian growth function with a carrying capacity q, by (3), where ξ denotes a tumor growth parameter. The dynamics for the endothelial support is described by (4), where bp models the stimulation of the endothelial cells by the tumor and the term \(dp^{\frac{2}{3}}q\) models the endogenous inhibition of the tumor. The coefficients b and d are growth constants. The terms μq and Guq describe, respectively, the loss to the carrying capacity through natural causes (death of endothelial cells, etc.), and the loss due to extra outside inhibition. The variable u represents the control in the system and corresponds to the angiogenic dose rate, while G is a constant that represents the anti-angiogenic killing parameter. More details on the descriptions and the discussion of parameters in (1)–(4) can be found in [9, 10]. They analyzed the above problem using first-order necessary conditions for optimality of a control u given by the Pontryagin maximum principle and the second order: the so-called strengthened Legendre–Clebsch condition and geometric methods of optimal control theory.

3 Hamilton–Jacobi Approach

For problems (1)–(4), we can construct the following Hamiltonian:

$$ \hat{H}(p,q,y,u):=\kappa u-y_{1}\xi p\ln \biggl(\frac{p}{q} \biggr)+y_{2}\bigl(bp-\bigl(\mu +dp^{\frac{2}{3}}\bigr)q-Guq\bigr), $$

where y=(y 1,y 2). The true Hamiltonian is

$$ H(p,q,y):=\min_{u\in \lbrack 0,a]}\hat{H}(p,q,y,u). $$

In spite that \(\hat{H}\) is linear in u, the control may not be determined by the minimum condition (detailed discussions are in [8]). Following [8], to exclude discussions about the structure of optimal controls in regions where the model does not represent the underlying biological problem, we confine ourselves to the biologically realistic domain

$$ D:= \bigl\{ (p,q): 0<p\leq \bar{p}, 0<q\leq \bar{q} \bigr\} , $$

where \(\bar{p}= ( \frac{b-\mu }{d} )^{3/2}\), \(\bar{q}=\bar{p}\). Thus, the Hamiltonian H is defined in D×R 2. We shall call trajectories admissible iff they satisfy (3), (4) (with control u∈[0,a]), and are lying in D. Along any admissible trajectory, defined on [0,T], satisfying necessary conditions—maximum Pontryagin principle [12], we have

$$ H\bigl(p(T),q(T),y(T)\bigr)=0,\quad \text{i.e.}\ H\bigl(p(t),q(t),y(t)\bigr)\equiv 0 \ \text{in}\ [0,T]. $$

However, as the problems (1)–(4) are free final time, we cannot apply directly the dynamic programming approach. The main reason is that in the dynamic programming formulation, the value function must satisfy the Hamilton–Jacobi equation (the first-order PDE) together with the end condition in final time. Thus, the final time should be fixed, or at least it should belong to a fixed end manifold. To this effect, we follow the trick of Maurer [12] and transform problems (1)–(4) into a problem with fixed final time \(\tilde{T}=1\). The transformation proceeds by augmenting the state dimension and by introducing the free final time as an additional state variable. Define the new time variable τ∈[0,1] by

$$ t:=\tau \cdot T,\quad 0\leq \tau \leq 1. $$

We shall use the same notation p(τ):=p(τ⋅T), q(τ):=q(τ⋅T) and u(τ):=u(τ⋅T) for the state and the control variable with respect to the new time variable τ. The augmented state

$$ \tilde{p}=p\in R^{1},\qquad \tilde{q}=\binom{q}{r}\in R^{2}, \quad r=T, $$

satisfies the differential equations

As a consequence, we shall consider the following augmented control problem (P̃) on the fixed time interval [0,1]:

$$ \min J(\tilde{p},\tilde{q},u):=\min J(p,q,r,u)=\min \biggl( \tilde{p}(1)+r\kappa \int_{0}^{1}u(\tau )\,d\tau \biggr) $$

s.t.

(5)
(6)

We shall call the trajectories \((\tilde{p},\tilde{q})\) (with control u∈[0,a]) admissible if they satisfy (5), (6), and (p,q) are lying in D. The transformed problem (\(\tilde{\mathrm{P}}\)) on the fixed interval [0,1] falls into the category of control problems treated in [13]. Thus, we can apply the dynamic programming method developed therein.

The Hamiltonian for the problem (\(\tilde{\mathrm{P}}\)) becomes

where \(\tilde{y}=(y_{1},y_{2},y_{3})\).

Define \(\tilde{D}:=[0,1]\times D\) and on it define the value function for the problem (\(\tilde{\mathrm{P}}\))

$$ S(\tau ,p,q):=\inf \biggl( \tilde{p}(1)+r\kappa \int_{\tau }^{1}u(s)\,ds \biggr) , $$
(7)

where the infimum is taken over all admissible trajectories starting at \((\tau ,p,q)\in \tilde{D}\). If it happens that S is of C 1, then it satisfies the Hamilton–Jacobi–Bellman equation [13]:

$$ \frac{\partial }{\partial \tau }S(\tau ,p,q)+\min_{u\in \lbrack 0,a]} \tilde{H}\biggl( \tilde{p},\tilde{q},\frac{\partial }{\partial p}S,\frac{\partial }{\partial q}S,u\biggr)=0, $$
(8)

with a terminal value

$$ S(1,p,q)=p,\quad (p,q)\in D. $$
(9)

Since the problems of the type (8)–(9) are difficult to solve explicitly in the paper [14] introduced the so-called ε-value function. For any ε>0, we call a function (τ,p,q)→S ε (τ,p,q), defined in \(\tilde{D}\), an ε-value function iff

(10)
(11)

It is also well known that there exists a Lipschitz continuous ε-value function and that it satisfies the Hamilton–Jacobi inequality:

Conversely [14]:

Each Lipschitz continuous function w(τ,p,q) satisfying

(12)

is an ε-value function; i.e., it satisfies (10)–(11).

In the next section, we describe a numerical construction of a function w satisfying (12).

4 Numerical Approximation of Value Function

This section is an adaptation of the method developed by Pustelnik in his Ph.D. thesis [15] for the numerical approximation of value function for the Bolza problem from optimal control theory. The main idea of that method is an approximation of the Hamilton–Jacobi expression from (12) by a piecewise constant function. However, we do not know the function w. The essential part of the method is that we start with a quite arbitrary smooth function g and then shift the Hamilton–Jacobi expression with g by the piecewise constant function to get an inequality similar to that as in (12). Thus, let \(\tilde{D}\ni (\tau ,p,q)\rightarrow g(\tau ,p,q)\) be an arbitrary function of class C 2 in \(\tilde{D}\), such that g(1,p,q)=p, (p,q)∈D. For a given function g, we define in \(\tilde{D}\times R^{+}\times U (\tau ,\tilde{p},\tilde{q},u)\rightarrow G_{g}(\tau ,\tilde{p},\tilde{q},u)\) as

(13)

Next, we define the function \((\tau ,\tilde{p},\tilde{q})\rightarrow F_{g}(\tau ,\tilde{p},\tilde{q})\) as

$$ F_{g}(\tau ,\tilde{p},\tilde{q}):=\min \bigl\{ G_{g}(\tau ,\tilde{p},\tilde{q},u):u\in U \bigr\} . $$
(14)

Note that the function F g is continuous in \(\tilde{D}\) and even Lipschitz continuous in \(\tilde{D}\), and denote its Lipschitz constant by \(M_{F_{g}}\). By the continuity of F g and compactness of \(\overline{\tilde{D}}\), there exist k d and k g such that

$$ k_{d}\leq F_{g}(\tau ,\tilde{p},\tilde{q})\leq k_{g}\quad \text{for }(\tau , \tilde{p},\tilde{q})\in \tilde{D} \times R^{+}. $$

The first step of approximation is to construct the piecewise constant function h η,g which approximate the function F g . To this effect, we need some notations and notions.

4.1 Definition of Covering of \(\tilde{D}\)

Let η>0 be fixed and \(\{q_{j}^{\eta }\}_{j\in \mathbb{Z}}\) be a sequence of real numbers such that \(q_{j}^{\eta }=j\eta \), j∈ℤ (ℤ—set of integers). Denote

$$ J:=\bigl\{j\in \mathbb{Z}: \text{there is}\ (\tau ,\tilde{p}, \tilde{q})\in \tilde{D}\times R^{+}, j\eta <F_{g}(\tau ,\tilde{p},\tilde{q})\leq (j+1)\eta \bigr\}, $$

i.e.

$$ J:=\bigl\{j\in \mathbb{Z}: \text{there is}\ (\tau ,\tilde{p},\tilde{q} )\in \tilde{D}\times R^{+}, q_{j}^{\eta }<F_{g}( \tau ,\tilde{p},\tilde{q})\leq q_{j+1}^{\eta }\bigr\}. $$

Next, let us divide the set \(\tilde{D}\) into the sets \(P_{j}^{\eta ,g}\), j∈J, as follows:

$$ P_{j}^{\eta ,g}:= \bigl\{ (\tau ,\tilde{p},\tilde{q})\in \tilde{D}\times R^{+}:q_{j}^{\eta }<F_{g}( \tau ,\tilde{p},\tilde{q})\leq q_{j+1}^{\eta} \bigr\} ,\quad j \in J. $$

As a consequence, we have for all i,j∈J, i≠j, \(P_{i}^{\eta ,g}\cap P_{j}^{\eta ,g}=\varnothing \), \(\bigcup_{j\in J}P_{j}^{\eta ,g}=\tilde{D}\) an obvious proposition.

Proposition 4.1

For each \((\tau ,p,q)\in \tilde{D}\), there exists an ε>0, such that a ball with center (τ,p,q) and radius ε is either contained only in one set \(P_{j}^{\eta ,g}\), j∈J, or contained in a sum of two sets \(P_{j_{1}}^{\eta ,g}\), \(P_{j_{2}}^{\eta ,g}\), j 1,j 2∈J. In the latter case, |j 1−j 2|=1.

4.2 Discretization of F g

Define in \(\tilde{D}\times R^{+}\) a piecewise constant function

$$ h^{\eta ,g}(\tau ,\tilde{p},\tilde{q}):=-q_{j+1}^{\eta },\quad (\tau ,\tilde{p},\tilde{q})\in P_{j}^{\eta ,g},\ j\in J. $$
(15)

Then, by the construction of the covering of \(\tilde{D}\), we have

$$ -\eta \leq F_{g}(\tau ,\tilde{p},\tilde{q})+h^{\eta ,g}(\tau , \tilde{p},\tilde{q})\leq 0,\quad (\tau ,\tilde{p}, \tilde{q})\in \tilde{D}\times R^{+}, $$
(16)

i.e., the function (15) approximates F g with accuracy η.

The next step is to estimate integral of h η,g along any admissible trajectory by the finite sum of elements with values from the set {−η,0,η} multiplied by 1−τ i , 0≤τ i <1. Let \((\tilde{p}(\cdot ),\tilde{q}(\cdot ),u(\cdot ))\) be any admissible trajectory starting at the point \((0,p_{0},q_{0})\in \tilde{D}\). We show that there exists an increasing sequence of m points {τ i } i=1,…,m , τ 1=0, τ m =1, such that, for τ∈[τ i ,τ i+1],

$$ \bigl \vert F_{g}\bigl(\tau_{i},\tilde{p}( \tau_{i}),\tilde{q}(\tau_{i})\bigr)-F_{g}\bigl( \tau ,\tilde{p}(\tau ),\tilde{q}(\tau )\bigr)\bigr \vert \leq \frac{\eta }{2},\quad i=1,\ldots ,m-1. $$
(17)

Indeed, it is a direct consequence of two facts: absolute continuity of \(\tilde{p}(\cdot )\), \(\tilde{q}(\cdot )\) and continuity of F g . From (17), we infer that, for each i∈{1,…,m−1}, if \((\tau_{i},\tilde{p}(\tau_{i}),\tilde{q}(\tau_{i}))\in P_{j}^{\eta ,g}\) for a certain j∈J, then we have, for τ∈[τ i ,τ i+1),

$$ \bigl(\tau ,\tilde{p}(\tau ),\tilde{q}(\tau )\bigr)\in P_{j-1}^{\eta ,g} \cup P_{j}^{\eta ,g}\cup P_{j+1}^{\eta ,g}. $$

Thus, for τ∈[τ i ,τ i+1] along the trajectory \(\tilde{p}(\cdot )\), \(\tilde{q}(\cdot )\),

$$ h^{\eta ,g}\bigl(\tau_{i},\tilde{p}(\tau_{i}), \tilde{q}(\tau_{i})\bigr)-\eta \leq h^{\eta ,g}\bigl(\tau , \tilde{p}(\tau ),\tilde{q}(\tau )\bigr)\leq h^{\eta ,g}\bigl( \tau_{i},\tilde{p}(\tau_{i}),\tilde{q}(\tau_{i}) \bigr)+\eta , $$
(18)

and so, for i∈{2,…,m−1},

$$ h^{\eta ,g}\bigl(\tau_{i},\tilde{p}(\tau_{i}), \tilde{q}(\tau_{i})\bigr)-h^{\eta ,g}\bigl(\tau_{i-1}, \tilde{p}(\tau_{i-1}),\tilde{q}(\tau_{i-1})\bigr)= \eta_{\tilde{p}(\cdot ),\tilde{q}(\cdot )}^{i}, $$
(19)

where \(\eta_{\tilde{p}(\cdot ),\tilde{q}(\cdot )}^{i}\) is equal to −η or 0 or η. Integrating (18), we obtain, for each i∈{1,…,m−1},

and in consequence,

Now, we will present the expression

$$ \sum_{i\in \{1,\dots ,m-1\}}\bigl[h^{\eta ,g}\bigl( \tau_{i},\tilde{p}(\tau_{i}),\tilde{q}( \tau_{i})\bigr) (\tau_{i+1}-\tau_{i})\bigr] $$

in a different, more useful form. By performing simple calculations, we get the two following equalities:

(20)

From (20), we get

and next, we obtain

and, taking into account (19), we infer that

(21)

We would like to stress that (21) is very useful from a numerical point of view: We can estimate the integral h η,g(⋅,⋅,⋅) along any trajectory \(\tilde{p}(\cdot ),\tilde{q}(\cdot )\) as a sum of finite number of values, where each value consists of a number from the set {−η,0,η} multiplied by τ m −τ i .

The last step is to reduce the infinite number of admissible trajectories to finite one. To this effect, we say that for two different trajectories: \(( \tilde{p}_{1}(\cdot ),\tilde{q}_{1}(\cdot ) ) \), \(( \tilde{p}_{2}(\cdot ),\tilde{q}_{2}(\cdot ) ) \), the expressions

$$ \sum_{i\in \{ {2,\ldots ,m-1} \} }\eta_{\tilde{p}_{1}(\cdot ), \tilde{q}_{1}(\cdot )}^{i}( \tau_{m}-\tau_{i})+h^{\eta ,g}\bigl(\tau_{1}, \tilde{p}_{1}(\tau_{1}),\tilde{q}_{1}( \tau_{1})\bigr) (\tau_{m}-\tau_{1}) $$

and

$$ \sum_{i\in \{ {2,\ldots ,m-1} \} }\eta_{\tilde{p}_{2}(\cdot ),\tilde{q}_{2}(\cdot )}^{i}( \tau_{m}-\tau_{i})+h^{\eta ,g}\bigl(\tau_{1}, \tilde{p}_{2}(\tau_{1}),\tilde{q}_{2}( \tau_{1})\bigr) (\tau_{m}-\tau_{1}) $$

are identical iff

$$ \bigl( p_{1}(\tau_{1}),q_{1}(\tau_{1}) \bigr) = \bigl( p_{2}(\tau_{1}),q_{2}( \tau_{1}) \bigr) = ( p_{0},q_{0} ) $$
(22)

and

$$ \eta_{\tilde{p}_{1}(\cdot ),\tilde{q}_{1}(\cdot )}^{i}=\eta_{\tilde{p}_{2}(\cdot ),\tilde{q}_{2}(\cdot )}^{i}\quad \text{for all}\ i\in \{2,\ldots ,m-1\}. $$
(23)

The last one means that in the set B of all trajectories \(\tilde{p}(\cdot ),\tilde{q}(\cdot )\) we can introduce an equivalence relation r: We say that two trajectories \(( \tilde{p}_{1}(\cdot ),\tilde{q}_{1}(\cdot ) ) \) and \(( \tilde{p}_{2}(\cdot ),\tilde{q}_{2}(\cdot ) ) \) are equivalent iff they satisfy (22) and (23). We denote the set of all disjoint equivalence classes by B r . The cardinality of B r , denoted by ∥B r ∥, is finite and bounded from above by 3m+1.

Define

It is easy to see that the cardinality of X is finite.

Remark 4.1

One can wonder whether the reduction of an infinite number of admissible trajectories to finite one makes computational sense, especially if the finite number may mean 3m+1. In the theorems below, we can always take infimum and supremum over all admissible trajectories and the assertions will be still true. However, from a computational point of view, they are examples in which it is more easily and effectively to calculate infimum over finite sets.

The considerations above allow us to estimate the approximation of the value function.

Theorem 4.1

Let \(( \tilde{p}(\cdot ),\tilde{q}(\cdot) ) \) be any admissible pair such that

$$ \bigl( p(\tau_{1}),q(\tau_{1}) \bigr) = (p_{0},q_{0} ) . $$

Then we have the following estimate:

Proof

By inequality (16),

$$ -\eta \leq F_{g}(\tau ,\tilde{p},\tilde{q})+h^{\eta ,g}(\tau , \tilde{p},\tilde{q})\leq 0, $$

we have

$$ -\eta -h^{\eta ,g}(\tau ,\tilde{p},\tilde{q})\leq F_{g}(\tau , \tilde{p}, \tilde{q})\leq -h^{\eta ,g}(\tau ,\tilde{p},\tilde{q}). $$

Integrating the last inequality along any \(( \tilde{p}(\cdot ),\tilde{q} (\cdot ) ) \) in the interval [τ 1,τ m ], we get

Thus, by a well-known theorem [16],

Hence, we get two inequalities:

and

Both inequalities imply that

As a consequence of the above, we get

and thus the assertion of the theorem follows. □

Now, we use the definition of equivalence class to reformulate the theorem above in a way that is more useful in practice. To this effect, let us note that, by definition of the equivalence relation r, we have

$$ \underset{ ( \tilde{p}(\cdot ),\tilde{q}(\cdot )) \in B_{\mathbf{r} }}{\inf } \biggl\{ -\sum_{i=2,\dots ,m-1} \eta_{\tilde{p}(\cdot ),\tilde{q} (\cdot )}^{i}(\tau_{m}-\tau_{i}) \biggr \} =\underset{x\in X}{\inf } \biggl\{ -\sum_{i\in \{ 1,\dots ,m-1 \} }x^{i}( \tau_{m}-\tau_{i}) \biggr\} $$

and

$$ \underset{ ( \tilde{p}(\cdot ),\tilde{q}(\cdot )) \in B_{\mathbf{r}}}{\sup } \biggl\{ -\sum_{i=2,\dots ,m-1} \eta_{\tilde{p}(\cdot ),\tilde{q} (\cdot )}^{i}(\tau_{m}-\tau_{i}) \biggr \} =\underset{x\in X}{\sup } \biggl\{ -\sum_{i\in \{ 1,\dots ,m-1 \} }x^{i}( \tau_{m}-\tau_{i}) \biggr\} . $$

Taking into account (21), we get

and a similar formula for supremum. Applying that to the result of the theorem above, we obtain the following estimation:

(24)

Thus, we come to the main theorem of this section, which allows us to reduce an infinite dimensional problem to the finite dimensional one.

Theorem 4.2

Let η>0 be given. Assume that there is θ>0, such that

(25)

Then

(26)

is εoptimal value at (τ 1,p 0,q 0) for ε=2η+θ.

Proof

From the formulae (24), (25), we infer

Then, using the definition of value function (7), we get (26). □

Example 4.1

Let the total amount of anti-angiogenic inhibitors A=300 mg (2). Take for initial values of tumor p 0=15502 and vasculature q 0=15500, κ=1. With u=10 (we assume maximum dose at which inhibitors can be given a=75 mg), taking an approximate solution of (3), (4), we jump to singular arc [8], and then follow it (in discrete way) until all inhibitors available are being used up, then final p=9283.647 and q=5573.07. We construct a function g numerically such that g(0,p 0,q 0)=9283.647 and assumption (25) is satisfied with θ=0, η=0.1 and \(h^{\eta ,g}(\tau_{1}, \tilde{p}(\tau_{1}),\tilde{q}(\tau_{1}))=0\).

5 Conclusions

The paper treats the free final-time optimal control problem in cancer therapy through the ε-dynamic programming approach stating that every Lipschitz solution of the Hamilton–Jacobi inequality is an ε-optimal value of the cost of the treatment. Then a numerical construction of the ε-optimal value is presented. As a final result, a computational formula for the ε-optimal value is given.