Renormalization of Collective Modes in Large-Scale Neural Dynamics

Abstract

The bulk of studies of coupled oscillators use, as is appropriate in Physics, a global coupling constant controlling all individual interactions. However, because as the coupling is increased, the number of relevant degrees of freedom also increases, this setting conflates the strength of the coupling with the effective dimensionality of the resulting dynamics. We propose a coupling more appropriate to neural circuitry, where synaptic strengths are under biological, activity-dependent control and where the coupling strength and the dimensionality can be controlled separately. Here we study a set of $N\rightarrow \infty$ strongly- and nonsymmetrically-coupled, dissipative, powered, rotational dynamical systems, and derive the equations of motion of the reduced system for dimensions 2 and 4. Our setting highlights the statistical structure of the eigenvectors of the connectivity matrix as the fundamental determinant of collective behavior, inheriting from this structure symmetries and singularities absent from the original microscopic dynamics.

1 Introduction

Equilibrium statistical mechanics is static in nature, its program being the reduction of a thermodynamically-large system to a handful of relevant variables and their equations of state. A major subprogram of nonequilibrium statistical mechanics consists of reducing a thermodynamically-large system to a handful of relevant variables and their dynamical laws.

We can describe this schematically as understanding under which conditions the the diagram in Fig. 1 commutes, i.e. when taking either branch leads to the same result.

At the top left we have our thermodynamically-large system, which lives in dimension $N_H$, ruled by a high-dimensional dynamical law. At the bottom right we have a low-dimensional space, the reduced variables, which live in dimension $N_L$. On the left branch, we first perform a detailed, costly and precise simulation of every variable in the system, and then we project this high-dimensional solution down into the lower-dimensional space. On the right branch, instead, we first project down the equations of motion themselves, to obtain an effective dynamics on the lower-dimensional subspace. Then we evolve the effective dynamics in its low-dimensional space. If we get the same low-D trajectories (or equivalent trajectories in some appropriately-defined sense) as a result of both branches, then we can say we have reduced our system.

Examples abound of this program having been carried out successfully; for example, Kadanoff’s demonstration that the coarsened dynamics of lattice-gas cellular automata [1] showed sound waves, led to the realization that cellular automata could be used to implement hydrodynamics. Closer to the subject of this Paper is the demonstration [2] that strongly coupled phase oscillators (Kuramoto style) obey certain low-dimensional dynamics, an example we shall revisit later. Finally a related subject which we shall not treat in any detail is that of hydrodynamical truncations, such as, e.g., the derivation of the 3D Lorenz equations from the (infinite-dimensional) equations for Bénard–Marangoni convection [3,4,5]. However, more systematic studies of this last example, under the light of amplitude equations derived a la Ginzburg–Landau, [6,7,8] as well as the analysis of the spatiotemporal organization in pattern-forming reaction-diffusion equations with similar methods, carry the germ of much of the philosophy that we intend to apply in our case, namely, the judicious study of the way in which a few unstable modes enslave the dynamics of many others. Indeed, complex Ginzburg–Landau equations ubiquitously appear in such a description for many non-equilibrium processes near the onset of instability provided that the interaction of the thermodynamically abundant components of the system interact only locally [9,10,11].

Fig. 1

An abstract view of the “effective description” program in statistical mechanics

We shall carry out this program for a particular setting within the theory of neural networks. A number of studies have highlighted the recurrent intracortical connections as a major determinant of the patterns of global activity within the cerebral cortex. For example, the spontaneous activity of individual units in primary visual cortex is strongly coupled to global patterns evincing the underlying functional architecture [12]: during spontaneous activity in the absence of input, global modes are transiently activated that are extremely similar to modes engaged when inputs are presented. Similarly in motor control it has been shown both in motor reach actions [13] as well as in songbirds [14] that motor gestures result in the transient activation of extended patterns of coherent activity. We have previoiusly argued that homeostatic mechanisms, such as those seeking to balance excitation and inhibition, will result in many dynamical modes of the system posing themselves close to the boundary between stability and instability [15]. Near the onset of instability, the spatial layout of such dynamical modes is determined as eigenvectors of a connectivity matrix [16]; their transient activation is then consistent with the eigenvalue of such an eigenvector being driven through the instability line, and back [14, 17].

We will try to therefore take a point of view in which we have as our two ingredients a cortical circuit, and a pattern of intracortical connections between copies of the same circuit. We thus consider an extremely abstract idealization of the connectivity of the cerebral cortex, in which we have cortical micro-columns (thought of, generally, as the vertical direction) with a prescribed complex intra-columnar circuit, laid out on a surface (thought of, generally, as horizontal). In general we shall have the neurons distributed on the product of a space describing the cortical column (say the interval I) times a space describing the surface (say the two-d plane $\mathbb R^{2}$). In general we shall have connections abstracted so that there are only connections within a column, or between homologous elements across columns, within the same layer; i.e. only horizontal or vertical connections, never diagonal. (This is reminiscent of some high-throughput computing architectures used for massively-parallel computing, such as the Anton supercomputer [18]). In keeping with a long tradition in computational neuroscience, we shall model the intercolumnar connectivity as being random [19]. Therefore our model will be on one side highly structured (the given cortical circuit) and on the other side entirely structureless (the random connectivity across columns).

The structure of this paper is as follows. We shall first introduce definitions and general framework. Then we introduce a specific simple example that under some circumstances we can actually solve in pretty closed form: a set of coupled oscillators. We will address increasingly complicated subproblems based on the nature of the coupling matrix: first, we will control a single real eigenvalue of a normal matrix, will give us a global equation in two degrees of freedom. Then we will study two complex-conjugate eigenvalues; this will give us a global equation in 4 degrees of freedom. Then we will show that there are interesting issues associated to having a non-normal connectivity matrix, namely one whose eigenvectors are not orthogonal. Finally, we will examine the explicit form of the mapping between microscopic and macroscopic modes, and show how it changes the smoothness class of the dynamics, making the global mode dynamical system less regular than the microscopic one. A careful study of this change in regularity permits us to give an explicit, closed-form answer as to under which conditions in the microscopic dynamics the program outlined in Fig. 1 can be successfully completed. At the end, we shall have given an explicit set of microscopic dynamics for which a proper global dynamics exists, and we shall compute this global dynamics explicitly.

2 Historical Note

This paper is dedicated to the memory of Leo P. Kadanoff, who was the postdoctoral mentor of OP, and the PhD thesis advisor of MM. It would be hard to express how much Leo shaped, not just this field, but the very process of how the authors reason, how we choose worthy problems, and how we try to train the younger generation.

In particular, Leo always made emphasis on using simple, highly stylized models as caricatures of a more general natural phenomenon one tried to understand, always keeping in mind what is the underlying program one is trying to push forward. His use of spin blocking to bring to the forefront the notion of averaging only over fluctuations at a given scale is emblematic, jokingly dubbed by his close friend Ken Wilson as an idea that “...although absurd, will be the basis of generalizations which are not absurd” [20]. The elegance with which such a simple setting shows that universal quantities like critical exponents are not a property of the underlying system, but rather a property (in this case an eigenvalue) of a change-of-scale operator, is a trademark of his work in general. Following Leo’s teachings, we will in this Paper outline a general program, and then solve very explicitly one small example in the program as to illustrate exactly where the conceptual emphasis should go.

We’ll miss his contributions as colleague and teacher. We shall also miss his personality and even his mannerisms. Leo was an astoundingly quick thinker and had a deep understanding, not just of Physics, but also of how physicists go about trying to solve problems. So during scientific discussions he often could foresee well ahead what was coming, often leaving his disciples with the feeling of having just been X-rayed. In the rare occasions one managed to catch him by surprise at a key point in the argument, he would lean back, briefly stare at the celing and proffer a curt yet solid “Ha!”, which was a much-sought and vied-for high mark of approval among us. It deeply saddens us we may never again receive that particular honor.

3 Definitions

Let us now establish the notation to be used in further detail, shown schematically in Fig. 3.

Again, at the top left we have our thermodynamically-large system: many variables $\mathbf{x} \in {\mathbb R}^{N_H}$ ruled by a high-dimensional dynamical law $\dot{\mathbf{x}} = f(\mathbf{x})$ given by a vectorfield f in ${\mathbb R}^{N_H}$, stated as $f \in {\mathcal T}({\mathbb R}^{N_H})$. At the bottom right we have a low-dimensional space, the reduced variables, which live in ${\mathbb R}^{N_L}$. On the left branch we first evolve in $N_H$ and then we use a projection operator $\Pi$ to project the high-dimensional solution down into the lower-dimensional space. On the right branch, instead, we first project down the equations of motion, to obtain an effective dynamics F on the lower-dimensional subspace: $F \in {\mathcal T}({\mathbb R}^{N_L})$. We call the projector operator for the equations $\Phi$; then $F = \Phi \{f\}$. Then we evolve this simpler dynamics $\dot{X} = F(X)$. If we get the same trajectories (or equivalent trajectories in some well-defined sense) as a result of both branches, then we can say we have reduced our system.

In addition to this projection, we may want to lift back those low-dimensional solutions onto the original space, to obtain a high-dimensional solution of the original equations. We call the lift operator $\Psi$.

Fig. 2

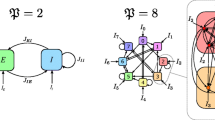
The abstraction of cortical structure we will employ here. Left a single cortical microcolumn consists of a circuit, where the degrees of freedom associated to each layer are coupled together via intracolumnar interactions. Each layer is labeled with a different letter. Right columns are replicated and indexed to form the cortical surface, and degrees of freedom are coupled laterally through lateral interactions staying within the same layer

Let’s start with a 3-D version to keep ideas clear, tracking Fig. 2. We say we have three layers x, y and z, and our differential equation connects them vertically to one another through a 3D vector field (f, g, h):

$$\begin{aligned} \dot{x}= & {} f(x,y,z)\\ \dot{y}= & {} g(x,y,z)\\ \dot{z}= & {} h(x,y,z) \end{aligned}$$

When replicated along N columns, we get N identical sets of uncoupled differential equations, one per column:

$$\begin{aligned} \dot{x}_i= & {} f(x_i,y_i,z_i)\\ \dot{y}_i= & {} g(x_i,y_i,z_i)\\ \dot{z}_i= & {} h(x_i,y_i,z_i) \end{aligned}$$

and then consider coupling all columns through layer x with a linear synaptic matrix M

$$\begin{aligned} \dot{x}_i= & {} f(x_i,y_i,z_i) + \sum _j M_{ij} x_j \nonumber \\ \dot{y}_i= & {} g(x_i,y_i,z_i)\\ \dot{z}_i= & {} h(x_i,y_i,z_i)\nonumber \end{aligned}$$

(1)

We’re left with N linearly coupled identical 3D equations in 3N variables. Much has been written about such systems, particularly in the area of coupled oscillators.

Fig. 3

Notation

A common way to study such systems is to define $M_{ij} = \lambda G_{ij}$, where $\lambda$ is a global coupling constant and $G_{ij}$ a graph connectivity matrix, whose elements are either 0 or 1, which can be used to describe the connections as occurring only along an underlying lattice. This is a standard setting in Physics, where the interaction strength is controlled by a physical constant and therefore affects all extant interactions in parallel. This approach leads to a changing effective dimensionality of the dynamical system, because as $\lambda$ is varied, all dynamical eigenvalues of the system move in unison, and hence the number of modes which can potentially enter the dynamics increases with increasing $\lambda$. We will take a different approach.

We shall assume the matrix M is under control from slow homeostatic processes, and that the stability of different eigenmodes is under biological control. To approach this goal in a graded fashion we shall begin by assuming that most of the eigensystem $(\lambda ^i,\mathbf{e}^i) \ni M \mathbf{e} = \lambda \mathbf{e}$ has strongly negative values. In addition we shall place the more specific hypothesis on the vector field (f, g, h) that when all eigenvalues $\lambda$ of M are sufficiently negative there exists a single, stable fixed point of the dynamics.

Then we shall allow either one single real eigenvalue or a couple of complex-conjugate eigenvalues to increase and approach the stability limits from the left.

A simple form of doing this is by first generating a base matrix $M_0$ with a given controlled spectrum. Following a long history of modeling studies, one can assume $M_0$ to be given by suitably-scaled i.i.d. Gaussian random variables [19] (See Sect. 6 below). Following this line of thought, in this work we shall either use $M_0$ as an $N \times N$ array of i.i.d Gaussians of variance 1 / N (spectrum in the unit disk in the complex plane, matrix almost surely non-normal) or the antisymmetric component of said $M_0$, $M_a = (M_0 - M^t_0)/\sqrt{2}$ (purely imaginary spectrum, matrix is normal). Then, a specific eigenvalue $\lambda _1$ (or pair of complex-conjugate eigenvalues) associated to an eigenvector $\mathbf e$ (again, pair of), is singled out and

$$\begin{aligned} M = M_{0/a} - \varLambda \mathbf{I} + (\varLambda + \lambda -\lambda _1) \mathbf{e_1}^t \mathbf{e_1} \end{aligned}$$

(2)

If our system has N columns and L layers, then its size is NL. The direction across layers is the rigidly-defined cortical circuit, and linear stability analysis may be performed on this circuit to obtain a Hessian matrix whose L eigenvalues determine the stability of one single column in isolation. The direction across columns is defined by an entirely unstructured random matrix, having N eigenvalue/eigenvector pairs defining the modes of behavior of the system. The system as a whole, then, has a stability structure given by NL eigenvalues that is a complex interplay of the structured column and the unstructured connections. For concreteness, assuming $L=3$, the system as a whole is given by a vectorfield of dimension 3N. The stability matrix of the whole system, namely the derivative matrix of the vectorfield, is then given by a matrix J of size $3N \times 3N$, which we can group as $3\times 3$ blocks of size $N \times N$, eight of which are diagonal:

$$\begin{aligned} J= \left[ \begin{array}{lll} \left[ {\partial {\dot{x}}_i \over \partial x_j }\right] &{}\quad \left[ {\partial {\dot{x}}_i \over \partial y_j }\right] &{}\quad \left[ {\partial {\dot{x}}_i \over \partial z_j }\right] \\ \left[ {\partial {\dot{y}}_i \over \partial x_j }\right] &{}\quad \left[ {\partial {\dot{y}}_i \over \partial y_j }\right] &{}\quad \left[ {\partial {\dot{y}}_i \over \partial z_j }\right] \\ \left[ {\partial {\dot{z}}_i \over \partial x_j }\right] &{}\quad \left[ {\partial {\dot{z}}_i \over \partial y_j }\right] &{}\quad \left[ {\partial {\dot{z}}_i \over \partial z_j }\right] \end{array}\right] = \left[ \begin{array}{ccc} M_{ij} + {\ \partial {f} \over \partial x } \delta _{ij} \ &{}\quad {\partial {f} \over \partial y}\delta _{ij} \ &{}\quad \ldots \\ {\partial {g} \over \partial x}\delta _{ij} &{}\quad {\partial {g} \over \partial y} \delta _{ij} &{}\quad \ldots \\ \ldots &{}\quad \ldots &{}\quad \ldots \end{array}\right] \end{aligned}$$

(3)

An explicit procedure for computing the eigenvalues of J from those of M will be discussed elsewhere.

Fig. 4

The eigenvalues of M in the complex plane. We shall construct M so that most eigenvalues have strongly negative real parts, around $-\varLambda$, while either one real or two complex-conjugate eigenvalues with real part $\lambda$ will be allowed to approach the imaginary axis

4 A Concrete Example: 2D Dynamics

We now consider a particular case which we can solve in pretty good detail, so as to concentrate on what are the central figures and concepts in this program. We will downgrade to the smallest non-trivial scenario, that of two layers so each column is a 2D differential equation; obviously it cannot do much more than have a number of fixed points and limit cycles. In what follows we will deal exclusively with the following

$$\begin{aligned} \begin{aligned} \dot{x}_i&= f(x_i) + y_i + \sum _j M_{ij} x_j \\ \dot{y}_i&= -x_i \end{aligned} \end{aligned}$$

(4)

where all the interesting dynamics has been subsumed into f(x).

For example, in the special case $f(x) = -x^3$ we have a van der Pol oscillator: taking the time derivative of the first equation, we obtain

$$\begin{aligned} \ddot{x}_i = -3\dot{x}_i x_i^2 - x_i + \sum _j M_{ij} \dot{x}_j \end{aligned}$$

We will show below we can evaluate the reduced dynamics for a Taylor series of f order-by-order, so some of what follows concentrates on $f(x)=x^\alpha$. But the main issue is the structure of M, whether it’s normal or non-normal; and whether we control a single real or two complex-conjugate eigenvalues.

As we shall see shortly, our procedure for obtaining the global dynamics from the microscopic dynamics involves both the right and the left eigenvectors of M. In general the matrix of left eigenvectors is the inverse of the matrix of right eigenvectors. However if M is normal, then the inverse reduces to the complex conjugate making their relationship much simpler. Therefore we shall explore first normal matrices and then examine the additional issues raised by non-normality. Within normal matrices we shall, as anticipated in Fig. 4, either control a single real eigenvalue or two complex-conjugate ones.

4.1 Single Real Eigenvalue, Normal Matrix

The simplest sub-case of Eq. (4) is that of a normal matrix M and a single real eigenvalue under control.

Antisymmetric matrices are normal. Thus consider M to be given by Eq. 2 with $M_a$, the antisymmetric component of a matrix of $N\times N$ i.i.d. Gausian variables of std $1/\sqrt{N}$; its eigenvalues are purely imaginary $\lambda = i \omega$ with imaginary component distributed like $p(\omega )\approx \sqrt{1-\omega ^2/4}$. Consider one of its null eigenvalues (one is guaranteed to exist if N is odd) and the corresponding eigenvector $\mathbf e$. Then define as per Eq. (2)

$$\begin{aligned} M_\lambda = M_a - \varLambda \mathbf{I} + (\varLambda + \lambda ) ( \mathbf{e e^\dag }) \end{aligned}$$

(5)

where $\mathbf e^\dag$ is the left (dual) eigenvector of $\mathbf e$. All eigenvalues of M, except for the null one we chose, get moved to $-\varLambda$, while the null one now has value $\lambda$.

Project Eq. (4) onto $\mathbf e$, defining $X \sqrt{N} = \mathbf{e^\dag \cdot x}$, so that X is of order 1, because $\mathbf{x \cdot x} \approx N$ while $\mathbf e \cdot e = 1$ so that $\mathbf{x \cdot e } \approx \sqrt{N}$ generically.

$$\begin{aligned} \begin{aligned} \dot{X} = \sum e^\dag _i \dot{x}_i&= -\frac{1}{\sqrt{N}} \sum e^\dag _i f(x_i) \ + Y + \lambda X \\ \dot{Y} = \sum e^\dag _i \dot{y}_i&= -X \end{aligned} \end{aligned}$$

(6)

Since we are considering a normal matrix and a real eigenvector, the right (dual) eigenvectors are the same as the right ones, transposed, so for the rest of this section we ignore the $\dag$. Evaluation of the $\sum e_i f(x_i)$ term is the key; assuming conversely that the projection of $x_i$ onto the space perpendicular to $\mathbf e$ is small (an assumption we shall revisit in detail below and elsewhere) we’d get an ansatz which is our first, naive approximation of the lift operator $\Psi$ (Fig. 3) which gives the microscopic variables as a function of the macroscopic ones $\mathbf{x} = \Psi [X]$:

$$\begin{aligned} \begin{aligned} x_i&\approx \sqrt{N} X e_i \\ y_i&\approx \sqrt{N} Y e_i \end{aligned} \end{aligned}$$

(7)

leading to

$$\begin{aligned} \begin{aligned} \dot{X}&= F(X) + Y + \mu X \\ \dot{Y}&= -X \end{aligned} \end{aligned}$$

(8)

where the coarse-graining operator $\Phi$, which transforms the microscopic dynamics to the coarsened dynamics

$$\begin{aligned} F \equiv \Phi [ f] \end{aligned}$$

is defined by

$$\begin{aligned} F(X) \equiv \frac{1}{\sqrt{N}} \sum _i e_i f( \sqrt{N} X e_i ) \end{aligned}$$

(9)

The first thing to notice is that $\Phi$ is linear in f, meaning we can try to apply it order-by-order in a Taylor expansion of f. Applying Eq. (9) to individual integer powers yields, in the large N limit, an evaluation of the moments of a Gaussian distribution:

$$\begin{aligned} \Phi [ x^\alpha ] = X^\alpha N^{{\alpha - 1}\over 2} \sum _i e_i^{\alpha +1} = {\left\{ \begin{array}{ll} \ \alpha !! \ X^\alpha &{}\quad \alpha \text { odd, } \\ \qquad 0 &{}\quad \alpha \text { even.} \end{array}\right. } \end{aligned}$$

(10)

The most important property to note is that the result is independent of which eigenvector $\mathbf{e}$ we chose, because under these circumstances the operator is self-averaging. Then, the power-law is unchanged except for a prefactor: the cubic $X^3$ nonlinearity gets renormalized by a factor of 3, $X^5$ by 15, $X^7$ by 105. Curiously this operator destroys all even nonlinearities. In subsequent work we shall prove that the even nonlinearities get absorbed in the overall shape of the center manifold, which we have assumed in the ansatz Eq. (7) to be linear in $x_i$. However the reduced equations (8) are not affected.

4.2 Complex-Conjugate Pair of Eigenvalues, Normal Matrix

As shown in Fig. 4, the second-simplest case is to control two complex-conjugate eigenvalues, as they can be controlled by a single parameter, their real part, while leaving their imaginary part unchanged.

We follow the previous section in using $M_a$, a normal matrix, as our base connectivity structure. Now we choose a pair of complex-conjugate eigenvalues. The corresponding eigenvectors are also complex conjugate. Choosing as $\mathbf{e}$ the one corresponding to the eigenvalue with positive imaginary part, the 2D subspace is spanned both by $\mathbf{e}$ and $\bar{\mathbf{e}}$, or by $\mathbf{e}_R \equiv \mathfrak {R}\mathbf{e}$ and $\mathbf{e}_I \equiv \mathfrak {I}\mathbf{e}$.

Following the previous section, and remembering that now the left eigenvector is the complex conjugate of the right eigenvector, $\mathbf{e}^\dag = \bar{\mathbf{e}}^t$ we define the coarse-grained variable X, now complex, as the normalized projection on $\mathbf{e}$:

$$\begin{aligned} X\sqrt{\dfrac{N}{2}} = \left( \mathbf{e}_{R}-\mathbf{e}_{I}i\right) \cdot \mathbf{x} \end{aligned}$$

Then the linear order approximation of the invariant manifold for the system:

$$\begin{aligned} \dot{x}_{i}= & {} y_{i}-x_{i}^{\alpha }+\underset{j}{\sum }M_{ij}x_{j}\\ \dot{y}_{i}= & {} -x_{i} \end{aligned}$$

gives us the linear order of $\Psi$

$$\begin{aligned} \mathbf{x}\approx & {} \sqrt{\dfrac{N}{2}}\left( X\left( \mathbf{e}_{R}+ i \mathbf{e}_{I} \right) +\bar{X}\left( \mathbf{e}_{R}-i \mathbf{e}_{I}\right) \right) \end{aligned}$$

Which, when applied to the base equation gives us the linear (naive) $\Phi$, for $\alpha$ odd:

$$\begin{aligned} \dot{X}= & {} Y-\ \alpha !! \ |X| ^{\alpha -1}X \ +\lambda X \\ \dot{Y}= & {} -X \end{aligned}$$

For $\alpha = 3$ this is a complex generalized van der Pol equation.

$$\begin{aligned} \dot{X}= & {} (\lambda - |X|^2) X + Y \\ \dot{Y}= & {} -X \end{aligned}$$

Notice the X equation is now a Hopf bifurcation normal form in a single complex variable, where $\mathrm{Imag}(\lambda )$ is the rotational frequency in the X complex plane, and $\mathrm{Real}(\lambda )$ is the control parameter, while the whole XY plane equation uses the same $\mathrm{Real}(\lambda )$ as a control parameter for a Hopf bifurcation in the real XY plane. Thus this equation contains 2 distinct frequencies, $\omega = 1$ from the base equation, and $\omega = \mathrm{Imag}(\lambda )$, the frequency of the eigenvector, from the complex X equation, and both cross the threshold of stability at the same time. Therefore, in this collective mode, a codimension-2 transition becomes generic, and the system in principle can bifurcate directly from a fixed point onto a torus. In this sense it is similar to a Takens–Bogdanoff normal form, only that it has two distinct and independent frequencies.

Thus the macroscopic equations are non-generic with respect to perturbations in the underlying microscopic dynamics in two ways: first, all even terms are destroyed, and second it can undergo a direct transition from a fixed-point to a torus.

4.3 Non-normal Matrices

In general, matrices are non-normal. Therefore to study general matrices we need to learn how to understand how non-normality affects our strategy.

In the non-normal case, evaluation of our $\Phi$ operator requires distinguishing between the left and right eigenvector in question, so Eq. (9) becomes

$$\begin{aligned} F(X) \equiv \sum _i e^L_i f( \sqrt{N} X e^R_i ) / \sqrt{N} \end{aligned}$$

(11)

which evidently demands that we understand the statistical structure not only of the right eigenvectors but also of the left (dual) ones. This is a somewhat vexing problem.

For normal matrices, eigenvectors are orthogonal and hence the matrix of left eigenvectors, the inverse of the matrix of right eigenvectors, can be simply obtained as the adjunct (complex conjugate transposed) of the right. However, when the matrix is not normal, the matrix of left eigenvectors has to be obtained the hard way, by inverting the matrix of right eigenvectors; the most important thing that happens is that the left eigenvectors are no longer normalized to $|e^\dag |=1$.

We now study what happens when, instead of choosing our base connectivity matrix to be the antisymmetric $M_a$, which is normal, we choose the standard random matrix $M_0$, which is non-normal. The eigenvalue expansion of $M_0$ is $E_R D E_L$ where D is a diagonal matrix with the eigenvalues on the diagonal, $E_R$ is the matrix of the right eigenvectors, and $E_L$, the matrix of left eigenvectors, satisfies $E_R E_L = I$.

While the matrix of right eigenvectors is, to lowest order, a matrix of i.i.d. Gaussian variables of standard deviation equal to $1/\sqrt{N}$, the matrix of left eigenvectors is not just substantially larger in magnitude, it is far from a Gaussian distribution. See Fig. 5.

Fig. 5

Histograms of the values of the elements of the matrix of left eigenvalues of $M_0$, a non-normal matrix of i.i.d. Gaussian variables. A histogram of the absolute values of the elements of the left eigenvalue matrix for the (nonsymmetric and nonnormal) i.i.d. Gaussian matrix. The values have a broad, heavy-tailed distribution broadly consistent with a power law tail

Quantitatively this stems from a simple reason. The right eigenvectors of $M_a$, by normality, must be a unitary matrix and thus all its eigenvalues lie on the unit circle in the complex plane. However, the right eigenvectors of $M_0$ are not orthogonal to one another, but they are still normalized to unity, reducing drastically the determinant of $E_R$. This reduction can only be due to the eigenvalues of $E_R$ lying inside the unit circle.

This effect is shown in Fig. 6.

Fig. 6

The eigenvalues of the matrix of right eigenvectors. Red normal case ($M_a$), they lie on the unit circle. Blue non-normal case ($M_0$), they form a funnel within the unit circle. This funnel is not uniform (i.e. no circle law) and the density increases for smaller radii; the smallest radius is proportional to $1/\sqrt{N}$. In this figure $N=1000$ and we have accumulated 10 instances (Color figure online)

The median determinant of an $N\times N$ Gaussian random matrix whose rows have been L2 normalized to 1 scales approximately like $\left( \frac{3}{5}\right) ^N$. On the other hand, the median determinant of the eigenvectors of said matrix go to zero much faster, with the log-linear plot displaying significant convexity. Furthermore, the probability distribution of the log said determinant is rather broad, as shown in Fig. 7.

Fig. 7

The determinant of the matrix of right eigenvalues (black) diminishes rapidly with dimension N. In fact it diminishes far faster than the determinant of a matrix of i.i.d. Gaussians whose rows have been normalized to 1 (red) (Color figure online)

5 Singularities

We have seen that our $\Phi$ operator can be applied to the vectorfield f order-by-order in a Taylor expansion. We now need to understand whether the resulting series converges and whether it can be resummed, in order to know whether we have succeeded in coarse-graining the dynamics. As we shall see, there exist f for which this can be done, and there exist f for which it can’t. In order to establish the boundary between them we need to understand how $\Phi$ affects the singularity structure of f.

It is a textbook point that in statistical mechanics the global behavior in the thermodynamic limit acquires singularities not present at finite N, which are phase transitions and other exotic objects. More technically, the partition function is assured smooth for finite N for local bounded interactions, but under some conditions acquires singular behavior for infinite N. As an exception, van Hove’s theorem assures us local interactions in a one-dimensional system cannot give rise to a phase transition at finite nonzero temperature.

In keeping with this general idea, in the soluble cases presented above, the $\Psi$ operator increases the singularity class of the vector field, by multiplying every odd term in the Taylor expansion with the double-factorial of the power.

Since the double factorial scales approximately like the square root of the factorial itself, this has peculiar consequences. If the function f has singularities, then $\Psi$ magnifies them so much that it may fail to converge at all. If the terms of the expansion of f decrease like 1 / n! (i.e. an exponential or sine), then the terms of F decrease like 1 / n!! (such as $\sin x^2$) and F is smooth.

The boundary case is when the terms in f decrease like 1 / n!!, in which case $\Psi$ generates a simple singularity. As an example,

$$\begin{aligned}&\Phi \left[ 1.2533\cdots * \tanh \left( {x \over 1.2533\cdots }\right) * \exp \big (+ x^2/2\big ) \right] \\&\quad =\, \Phi \left[ \sum _i { x^{2i+1}\over (2i+1)!!} \right] = \sum _i x^{2i+1} = { x \over { 1 - x^2 }} \end{aligned}$$

I.e. $\Phi$ acting on a function that increases like the inverse of a Gaussian generate poles at finite distance from the origin.

Thus the peculiar structure of $\Phi$ permits us to make general statements about under which vectorfields will the diagram of Fig. 3 commute.

6 Context

When pitted against the seemingly unfathomable depth of complexity within living beings, it is a natural “zero information” approach to modeling to assume the structure of interactions is, for all practical purposes of the modeler, structureless, a jumble of random numbers and noise. A classical embodiment of this line of thought are Kauffman nets [21, 22], a modelization of transcriptional regulation networks as random boolean nets that was instrumental in highlighting the intrinsically dynamical nature of cell differentiation. In this family of models, the complex web of transcriptional regulation is described as a random boolean network, its fixed-point attractors representing steady, self-consistent states of transcriptional activation that Kauffman equates to stable cell fate types; differentiation then being a process of climbing over metastable barriers separating basins of adjacent fixed points.

In neuroscience, a fruitful line of inquiry started with the Sompolinsky family of neural net models, which assume as a basis an interaction structure given by a Gaussian random matrix scaled to have a spectrum in the unit disk, and the overall excitatory/inhibitory balance set so the unit disk is displaced to the left until it osculates the imaginary axis [19]. These results have been particularly instrumental as a beachhead in the study of recurrent neural networks, which have otherwise proved to be resilient to analysis.

Using this connectivity as their basis, a long series of works shows that by careful tampering with such a structure one may achieve a number of useful ends, with a notable flurry of recent activity [23,24,25,26,27,28,29,30,31].

In previous work [15] it was shown that certain slow dynamics to evolve the connectivity structure itself, such as anti-Hebbian evolution, could result in drastic re-shaping of the eigenvalue distribution, where eigenvalues were flattened onto the imaginary axis, the edge of stability for the model.

In this Paper we shall work with a network that is not structureless as in the previous paragraphs, but rather has a “cross product” structure between a rigidly-defined object (the column) and a random-structure connectivity (across columns). This structure, though simplistic, can be viewed as a useful approximation to the structure of cortex, where the intracolumnar dynamics is largely defined by anatomy, while the recurrent intercolumnar dynamics may be usefully modeled as mostly random, within various degrees of geometrical restriction. The eigenspectrum of our system is therefore determined in equal measure by the rigid intracolumnar connectivity as well as the random intercolumnar interactions. As the aim of the current paper is to derive the coarse-grained dynamics (the “eigencolumn”) from the microscopic dynamics, we assumed a level of control over the spectrum which is bound to be somewhat unrealistic for biological structures. In further work, this restriction will be relieved gradually, as the setting allows for evaluating the interactions between multiple active “eigencolumns”. See Fig. 8 for a summary.

Fig. 8

The eigenspectra of the interaction matrix in three models. a The Sompolinsky–Abbott family of models assumes as it basic state a matrix of i.i.d. Gaussians of variance 1 / N (thus the spectrum is the unit disk) displaced to the left by $-1$ so that the spectrum osculates the imaginary axis. Various strategies for modifying the underlying connectivity allow this model to display a remarkably large variety of behaviors. b The “self-tuned-critical” model [15] allows a matrix like in a to be modified by anti-Hebbian interactions; the result of such a dynamics is to stably flatten the entire cloud of eigenvalues onto the imaginary axis. The price to pay for this stabilization is that the eigenvalue dynamics never stops evolving, as all eigenvalues ceaselessly flutter around the imaginary axis. c The model considered here, starts by pushing most of the eigenvalue cloud to the stable region in the left, leaving only a number of modes active. The aim of such a procedure is not to model a specific brain process, but rather to be able to derive the laws of motion of each collective mode from the microscopic dynamics, and subsequently to derive the interactions between multiple modes. Please carefully note that what is displayed is the spectrum of the interaction matrix; the spectrum of the system as a whole is determined both by this interaction matrix as well as the Hessian of the internal dynamics of each column as described in Eq. (3)

7 Conclusions

There are a number of points to be made at this juncture. First, that under certain circumstances this procedure converges properly and the diagram of Fig. 1 commutes: we can obtain in closed form the coarse-grained dynamics.

Second, our reduction procedure depends crucially on the structure of the eigenvectors. After more than 60 years of interest in eigenvalue statistical structure, and a tour-de-force theorem [32] for the circular law, a lot is now understood about them. Still remarkably little is known about the structure of the eigenvectors of such matrices, which display much less universality than the eigenvalues; [33] was one of the first studies of eigenvectors of nonnormal random matrices. Basic results link the PDF of entries in the eigenvector to the PDF of the matrix entries [34], and a fair amount of effort has been spent in understanding localization of eigenvectors in nearly-one-dimensional systems; see [35] for a recent review.

Simple numerical exploration leads us to conjecture that a great deal about the geometrical structure of the network gets encoded into the statistical structure of the eigenvalues. To illustrate why, let us consider a simple example: a 2D toroidal (periodic boundary conditions) lattice of size $M\times M$, in which elements are connected by a random Gaussian term if they are ${\le }3$ lattice units apart. There are 28 such near neighbors for each site. There are $N=M^2$ sites, and hence the interaction matrix is $N\times N = M^4$; this matrix is sparse because every row contains 29 nonzero elements (including the diagonal) no matter how large M is. Since the banded structure of the matrix exceeds $\sqrt{N}=M$ this construction narrowly escapes localization [35]. The spectrum of this matrix is still circular, following the strong universality results for the spectrum of sparse matrices; but the eigenvectors have a strongly interdependent statistical structure. The reason is simple: we are using $29 M^2$ random numbers are used in order to generate $M^2$ eigenvalues and $M^2$ eigenvalues with $M^2$ coefficients (minus one for normalization). Therefore the eigenvectors are not merely correlated: they are not statistically independent from one another, and they become more and more codependent the larger the value of M. Our reduction operator is extremely sensitive to these dependencies, and we conjecture that the ambient space in which the columns are embedded gets encoded into these interdependencies.

Third, this procedure generates symmetries where there were no symmetries to begin with. In the current case, the global dynamics is always an odd vector field. This can lead to curious situations, in which the dynamics of the individual column is unstable (say due to a $x^2$ or $x^4$ term), but the reduced dynamics is a globally attractive limit cycle.

Finally, in classical statistical mechanics a notorious feature is that the system as a whole can develop singularities such as phase transitions where the underlying system was perfectly smooth. Like in statistical mechanics, the global dynamics is of a slightly smaller regularity class than the microscopic dynamics, as multiplication by the double-factorial of N makes the Taylor expansion less convergent. For example, if the microscopic dynamics f has a pole, then F is nowhere-convergent and the dynamics is not coarse-grainable through the method presented in this Paper. If, on the other hand, f is holomorphic, it may stay holomorphic because the double factorial is approximately the square root of the factorial for sufficiently large arguments. On the other hand certain holomorphic functions get mapped onto functions with poles, increasing their singularity class.

We shall present elsewhere a more rigorous approach using center manifold reductions to a higher order than here, and show that it accurately captures numerical simulations. In further work we shall concentrate on controlling multiple modes and deriving their laws of interaction, as well as examining matrices M with more interesting structure, such as locality in an embedding ambient space.