Growth of Uniform Infinite Causal Triangulations

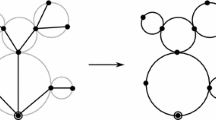
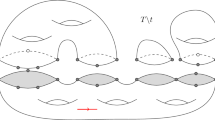
Abstract

We introduce a growth process which samples sections of uniform infinite causal triangulations by elementary moves in which a single triangle is added. A relation to a random walk on the integer half line is shown. This relation is used to estimate the geodesic distance of a given triangle to the rooted boundary in terms of the time of the growth process and to determine from this the fractal dimension. Furthermore, convergence of the boundary process to a diffusion process is shown leading to an interesting duality relation between the growth process and a corresponding branching process.

Appendices

Appendix A: Proofs of Basic Lemmas

1.1 A.1 Proof of Lemma 3.2

Let $\mathcal{F}_{n}=\sigma(M_{0},M_{1},\dots,M_{n})$. Recall that ξ _n =M _n+1−M _n . We thus have $M_{n} \in\mathcal{F}_{n}$ and $\xi_{n} \in\mathcal{F}_{n+1}$. On {M _n ≥1} one has

$$ \operatorname{E{}}(\xi_n|\mathcal{F}_n) =1\cdot\frac{1}{2} \biggl(1+\frac{1}{M_n} \biggr)-1\cdot \frac{1}{2} \biggl(1-\frac{1}{M_n} \biggr)=\frac{1}{M_n}. $$

(A.1)

Note also that

$$ \xi_n^2=1. $$

(A.2)

Consider $X_{n}=M_{n}^{2}-3n$. Let us prove that X _n is a martingale adapted to $\mathcal{F}_{n}$. Evidently $X_{n} \in\mathcal{F}_{n}$ and $\operatorname{E{}}|X_{n}|< \infty$. Therefore, we only need to check that $\operatorname{E{}}(X_{n+1}|\mathcal{F}_{n})=X_{n}$. Using (A.1)–(A.2) we have

Thus one gets

and therefore,

(A.3)

With any sequence of positive numbers {a _m } consider

$$B_n=\sum_{m=1}^n \frac{X_m-X_{m-1}}{a_m}. $$

Using the fact that X _n is a martingale, it is easy to check that B _n is also a martingale. One has

From (A.3), we get that if a _m =mlogm, then there exists a constant C>0 such that $\operatorname {E{}}B_{n}^{2}<C<\infty$. Therefore, using the L ^p convergence theorem (see e.g. Theorem 4.5 from Chap. 4 of [22]), one has that B _n converges a.s. Using Kroneker’s Lemma (see e.g. Lemma 8.5 from Chap. 1 of [22]), we see that $\frac{X_{n}}{n \log n}\to0$ a.s. and recalling the definition of X _n , one gets Lemma 3.2.

1.2 A.2 Proof of Lemma 3.3

This proof proceeds using a similar strategy as the previous proof. Consider

$$X_n=M_n-\sum_{i=1}^n \frac{1}{M_i}. $$

From (A.1) it follows that X _n is a martingale adapted to $\mathcal{F}_{n}$. Using the fact that |ξ _n |=1 and M _n ≥1 for any n, we have

$$ \operatorname{E{}}(X_{n+1}-X_n)^2 =\operatorname{E{}} \biggl(\xi_n-\frac{1}{M_{n+1}} \biggr)^2 \le4. $$

(A.4)

Consider further

$$B_n=\sum_{m=1}^n \frac{X_m-X_{m-1}}{a_m}. $$

Using the fact that X _n is a martingale, one has again that B _n is also a martingale and we have

Using (A.4), we get that if $a_{m}=\sqrt{m}\log m$, then $\sup_{n}\operatorname{E{}}B_{n}^{2}<\infty$. Using the L ^p convergence theorem, we observe that B _n converges a.s. Finally, using Kroneker’s Lemma as before, we see that $\frac{X_{n}}{\sqrt{n} \log n}\to0$ a.s. Recalling the definition of X _n , we get Lemma 3.3.

Appendix B: Convergence of Markov Chains to Diffusion Processes

To prove Theorem 4.1 we need a little background on stochastic differential equations and convergence to diffusion. The following definition and theorem can for instance be found in [23] Chaps. 5 and 8, where the latter is a rather good introduction to the topic which itself is based on [24–26].

Definition B.1

We say that X _t is a solution to the martingale problem for b and σ ², or simply X solves MP(b,σ ²) if

$$X_t -\int_0^t b(X_s) ds\quad\text{and}\quad X_t^2 -\int _0^t \sigma (X_s)^2 ds $$

are local martingales. Further, we say that the martingale problem is well-posed if there is uniqueness in distribution and no explosion.

Let us now consider a Markov chain $Y^{(h)}_{mh}$, m≥0, taking values in a set $\mathcal{X}_{h}\subset\mathbb{R}$ and having transition probabilities

$$p^h(x,A):=\mathbb{P} \bigl[Y^{(h)}_{(m+1)h}\in A \big| Y^{(h)}_{mh}=x \bigr], \quad x\in \mathcal{X}_h, \ A\subseteq\mathbb{R}. $$

Further, set $X_{t}^{(h)}=Y^{(h)}_{h [t/h]}$ and define

with B(x,ϵ)={y:|y−x|<ϵ}.

The following theorem (see e.g. [23], Theorem 8.7.1) proves convergence of the Markov chain to a limiting diffusion:

Theorem B.1

Suppose that b and σ are continuous functions for which the martingale problem is well-posed and for R<∞ and ϵ>0

• (1) $\lim_{h\to0}\sup_{|x|\leq R} |\sigma^{2}_{h}(x)-\sigma^{2}(x) |=0$

• (2) lim _h→0sup_|x|≤R |b _h (x)−b(x)|=0

• (3) $\lim_{h\to0}\sup_{|x|\leq R} \Delta_{h}^{\epsilon}(x)=0$

If $X^{(h)}_{0}\to x$ then we have $X^{(h)}_{t} \Rightarrow X_{t}$, in the sense of weak convergence on the functions space D[0,∞), where the continuous process X _t is diffusive and solves the following Itô’s equation

$$dX_t=b(X_t)dt + \sigma(X_t) dB_t, \quad X_0=x. $$

The following is a well-known theorem from stochastic calculus (see e.g. [23], Theorem 5.6.1) regarding random time changes of a stochastic process:

Theorem B.2

Let X _u be a solution of the martingale problem MP(b,σ ²) for u∈[0,∞), let g be a positive function and suppose that for all u∈[0,∞)

$$\tau_u = \int_0^u g(X_s) ds<\infty. $$

Define the inverse of τ _u by $\tau^{-1}_{s}=\inf\{ t: \tau_{t}>s\}$ and let $Y_{s}=X_{\tau^{-1}_{s}}$, then Y _s is a solution of MP(b/g,σ ²/g).