Network Complexity and Parametric Simplicity for Cargo Transport by Two Molecular Motors

Abstract

Cargo transport by two molecular motors is studied by constructing a chemomechanical network for the whole transport system and analyzing the cargo and motor trajectories generated by this network. The theoretical description starts from the different nucleotide states of a single motor supplemented by chemical and mechanical transitions between these states. As an instructive example, we focus on kinesin-1, for which a detailed single-motor network has been developed previously. This network incorporates the chemical transitions arising from ATP hydrolysis on both motor heads. In addition, both the chemical and the mechanical transition rates of a single kinesin motor were found to depend on the load force experienced by the motor. When two such motors are attached via their stalks to a cargo particle, they become elastically coupled. This coupling can be effectively described by an elastic spring between the two motors. The spring extension, which is given by the deviation of the actual spring length from its rest length, determines the mutual interaction force between the motors and, thus, affects all chemical and mechanical transition rates of both motors. As a result, cargo transport by two motors leads to a combined chemomechanical network, which is quite complex and contains a large number of motor cycles. However, apart from the single motor parameters, this complex network involves only two additional parameters: (i) the spring constant of the elastic coupling between the motors and (ii) the rebinding rate for an unbound motor. We show that these two parameters can be determined directly from cargo trajectories and/or trajectories of individual motors. Both types of trajectories are accessible to experiment and, thus, can be used to obtain a complete set of parameters for cargo transport by two motors.

1 Introduction

Molecular motors are biological machines that perform mechanical work on the nanometer scale within living organisms. We will be concerned with cytoskeletal motors that walk along cytoskeletal filaments and transport intracellular cargo such as vesicles or whole organelles [1–3]. Three superfamilies of such motors have been identified: kinesin, dyneins, and myosins. All of these motors are powered by the hydrolysis of adenosine triphosphate (ATP) into adenosine diphosphate (ADP) and inorganic phosphate (P). We will focus here on conventional kinesin or kinesin-1, which has been studied by many single molecule experiments, see, e.g., [4–7], and for which we have a good theoretical description on the single motor level [8, 9].

Conventional kinesin or kinesin-1 motors are tetramers consisting of two identical heavy chains, which fold into two enzymatic motor domains or heads, and two identical light chains, which mediate the binding to cargo particles in vivo [3]. Each motor head contains a nucleotide binding pocket for the binding and hydrolysis of ATP and a microtubule binding site, by which the head can attach to the filament. A rather flexible necklinker combines the two chains into dimeric or two-headed kinesin.

Single kinesin motors have been typically studied using bead assays, in which the motor is attached to a bead that can be manipulated by an optical trap, see, e.g. [4–6]. It is known that kinesin is a processive motor [10] that walks in discrete steps of 8 nm [11] towards the plus end of microtubuli [12]. On average, it makes about 100 steps [13] in a hand-over-hand fashion [14, 15] before it detaches from the filament. During each mechanical step, kinesin hydrolyzes one ATP molecule [16, 17]. The mechanical steps are fast and completed within 15 μs [4] whereas the chemical transitions take several ms [18, 19]. Furthermore, in the presence of a sufficiently large load force, kinesin performs frequent backward steps [4, 20].

As shown in [8, 9], all of these observations, which have been obtained by different experimental groups, can be described quantitatively by a network theory for single kinesin-1 motors. This theory is based on discrete motor states as defined by the nucleotide occupancy of the two motor heads as well as chemical and mechanical transitions between these states. One important property of these networks is that they involve several motor cycles, which provide the free energy transduction between ATP hydrolysis and mechanical work. As one varies the nucleotide concentrations and the external load force, the fluxes on these cycles change and different cycle fluxes dominate for different parameter regimes. In this sense, the chemomechanical networks of a single motor as introduced in [8, 9] contain several competing motor cycles.

In vivo, cargo transport is usually performed by small teams of motors that may belong to the same or to different motor species, see, e.g., [21–23]. Each motor of such a team has a finite run length, after which it unbinds from the filament. Furthermore, such an unbound motor is likely to rebind to the filament as long as the cargo is still connected to the filament by the other motors. As a consequence, the number of actively pulling motors is not fixed but fluctuates. The associated binding and unbinding processes are stochastic and have been shown, in previous theoretical studies, to play a crucial role for the overall transport properties of cargos that are transported by teams of identical motors [24, 25], by two teams of antagonistic motors that perform a stochastic tug-of-war [26, 27], and by an actively pulling team supported by a passively diffusing team [28, 29]. Experimental observations, both in vitro [30–35] and in vivo [36, 37] confirm the importance of stochastic motor binding and unbinding as predicted theoretically.

In our previous theoretical studies on cooperative cargo transport [24–28], the chemical and mechanical transitions of the single motors, which determine the free energy transduction of these motors, were not taken into account explicitly but only implicitly via the resulting force-velocity relationships. In the present study, we will introduce and study a more detailed theoretical description, in which we take the chemomechanical motor cycles of the individual motors into account. In this refined theory, each of the four motor heads of the two dimeric motors can bind ATP, hydrolyze it into ADP and P, and subsequently release the latter nucleotides, first P and then ADP. The reverse chemical reactions corresponding, e.g., to ADP binding and ATP synthesis, are also included as well as the coupling of these chemical reactions to the forward and backward mechanical steps. It is important to note that all of these transitions are stochastic as well. Furthermore, we impose cyclic balance conditions [9, 38] on all motor cycles, which ensures that the network description satisfies both the first and second the law of thermodynamics.

We focus on a pair of kinesin-1 motors and start from the chemomechanical network for a single motor as developed in [8, 9]. We couple the two motors by their stalks to a cargo particle and describe these two stalks as elastic springs. Since these two springs are only coupled via the cargo, which is taken to be rigid, we can replace them by one spring with an effective spring constant, the coupling parameter K. This elastic coupling generates a mechanical force between the two motors, as soon as one of these motors performs a mechanical forward or backward step. It is important to note that the force arising from a mechanical step of one motor affects the chemical and mechanical transition rates of both motors. As a result, we obtain a uniquely defined chemomechanical network for the motor pair. Even though this network is rather complex and contains a large number of motor cycles, it involves only two additional parameters: the coupling parameter K as well as the rebinding rate π _si of a single motor.

In the main part of this paper, the chemomechanical network of the motor pair is used to generate trajectories of the individual motors and, thus, of the cargo. These trajectories can always be decomposed into 1-motor and 2-motor runs, during which the cargo is actively pulled by one and two motors, respectively. During 1-motor runs, the cargo performs 8 nm steps whereas it performs 4 nm steps during 2-motor runs. These different step sizes can be distinguished by optical microscopy. Once the 1- and 2-motor runs of the cargo trajectories have been identified, the statistics of these runs can be used to extract reliable estimates of the two additional parameters of the motor pair as provided by the coupling parameter K and the rebinding rate π _si of a single motor. First, the rebinding rate π _si can be directly obtained from the average run time of the 1-motor runs. Second, the average run time of 2-motor runs is related to the termination rate of these runs, and this latter rate can be used to determine the coupling parameter K.

An alternative method to determine the two additional parameters is based on the statistical analysis of individual motor trajectories. From an experimental point, the observation of these latter trajectories is more demanding but is, in principle, feasible as has been recently shown for the individual heads of the dynein motor [39]. The rebinding rate π _si can again be obtained from the 1-motor runs, for which one of the individual motor traces is missing. Furthermore, the individual motor trajectories determine the time-dependent motor-motor separations, and the distribution of these separations can be used to deduce the coupling parameter K.

Our paper is organized as follows. In Sect. 2, we describe our network representation for single kinesin motors. Compared to [8], the force dependence of the chemical transitions is slightly modified. The theoretical description of the motor pair is introduced in Sect. 3: The basic force balance between the two motors is explained in Sect. 3.1, the combined network representation in Sect. 3.2. The combined network is then used to generate trajectories both of the individual motors and of the cargo. The corresponding simulation method is described in Sect. 4. The statistical properties of the cargo trajectories are analyzed in Sects. 5–7, where we discuss the dwell times of the cargo, the average run times of 1- and 2-motor runs as well as the relative frequency of these two types of runs. In Sect. 8, we show how to extract the two parameters π _si and K from these statistical properties of the cargo trajectories. The analysis of individual motor trajectories and the resulting distribution of motor-motor separations, which provide an alternative method to deduce the two parameters π _si and K, is discussed in Sect. 9. At the end, we summarize our results and give a brief outlook.

2 Single Motor Behavior

The dynamics of a single motor can be described by a continuous-time Markov process on a discrete state space or network [8, 9, 40], the nodes of which represent different chemical states of the two motor heads and the edges describe transitions between these states, see Fig. 1.

Fig. 1

Chemomechanical network of kinesin: The nucleotide binding pocket of each motor head can be empty (E), occupied by ATP (T), or occupied by ADP (D). In general, the two-headed motor can then attain 3²=9 states but two of these states, namely EE and TT, should not play any prominent role for the processive motion of kinesin, since, for these two states, both motor heads are strongly bound to the microtubule. Neglecting the states EE and TT, one arrives at the 7-state network shown here. The dashed line represents the mechanical stepping and the filled arrows indicate the direction of the ATP hydrolysis that takes place during the transitions |61〉, |34〉 and |57〉. The transition |25〉 corresponds to the mechanical forward step which implies the convention that the leading head of the dimeric motor is the one on the right, whereas the trailing head is the one on the left. Motor dissociation from the filament is only possible if the motor is in the DD state. The unbound motor state will be denoted by i=0 and represents an absorbing state as far as the directed walks of a single motor are concerned. The forward cycle $\mathcal{F}$ contains the mechanical forward step |25〉 and the backward cycle $\mathcal{B}$ the mechanical backward step |52〉. The thermal slip cycle $\mathcal{T}$ includes hydrolysis |57〉 and synthesis |16〉 of one ATP molecule without mechanical stepping

2.1 Motor States and Transitions

A single motor head can attain three states: Its nucleotide binding pocket can be empty (E), contain ATP (T) or ADP (D). Two motor heads can then occupy 3²=9 states, each of which is connected to four other states via chemical transitions that describe the binding or release of ATP or ADP as well as the combined process of ATP cleavage and the release of P. If the motor head is empty or contains ATP, it is strongly bound to the filament while it is only loosely bound to the filament if it contains ADP [41]. Thus, the two states EE and TT are characterized by two strongly bound heads and should be irrelevant for the processive motion of kinesin. Neglecting these two states, one arrives at the 7-state network as shown in Fig. 1 [8].

The seven states of the chemomechanical network in Fig. 1 will be labeled by i=1,…,7 and the transitions |ij〉 from state i to j are described by the transition rates ω _ij . In the network, the transition |ij〉 corresponds to a directed edge (or di-edge) whereas a non-directed edge will be denoted by 〈ij〉. In Fig. 1, the direction of the ATP hydrolysis is indicated by filled arrows and takes place during the transitions |61〉, |34〉 and |57〉. The mechanical step is marked by the dashed edge, which represents both the mechanical forward step |25〉 and the mechanical backward step |52〉. The motor can dissociate with unbinding rate ω ₇₀ from state i=7, in which both heads contain ADP and the motor is loosely bound to the filament [41], to the unbound motor state i=0, which represents an absorbing state as far as the directed stepping of the motor along the filament is concerned.

2.2 Motor Cycles and Dicycles

The network graph in Fig. 1 has six cycles $\mathcal {C}_{\nu}$, three of which are fundamental cycles in the sense of mathematical graph theory [42]: The forward cycle $\mathcal{F}=\langle12561 \rangle$, the backward cycle $\mathcal{B}=\langle45234 \rangle$ and the thermal slip cycle $\mathcal{T}=\langle16571 \rangle$. The directed cycles of dicycles $\mathcal{F}^{+}=|12561 \rangle$ and $\mathcal{B}^{+}=|45234 \rangle$ both involve the hydrolysis of a single ATP molecule couple to a single mechanical step whereas the dicycles $\mathcal{T^{+}}$ and $\mathcal{T^{-}}$ involve both the hydrolysis of one ATP molecule and the synthesis of such a molecule. The alternative forward cycle $\mathcal{F}_{DD}=\langle12571 \rangle$ and the two enzymatic slip cycles $\mathcal {E}=\langle1234561 \rangle$ and $\mathcal {E}_{DD}=\langle1234571 \rangle$ during which two ATP molecules are hydrolyzed without mechanical stepping, can be constructed as linear combinations of the fundamental cycles. By convention, a dicycle $\mathcal{C}_{\nu}^{+}$ is completed in the counter-clockwise direction.

The transition |25〉 corresponds to the mechanical forward step. Thus, we use the implicit convention in Fig. 1 that the leading head of the dimeric motor is the head on the right, whereas the trailing head is the one on the left. Therefore, the network contains pairs of states that can be transformed into each other by swapping the positions of the leading and the trailing head. It seems plausible to assume the chemical transition rates between the different motor states do not depend on the spatial ordering of the two heads. However, because each cycle is characterized by a certain balance condition and because the rates for forward and backward mechanical stepping are very different, at least one chemical transition of the cycle $\mathcal{B}$ must be different from the corresponding transition of the cycle $\mathcal{F}$. As in Ref. [8], we choose this transition to be |54〉, the rate of which is then determined by the balance conditions rather than by the rate of the transition |21〉.

2.3 Parametrization of Transition Rates

The transition rates ω _ij between two states i and j depend on the molar nucleotide concentrations [X], with X= ATP, ADP or P, and on the load force F. It will be convenient to express the force dependence in terms of the dimensionless force

(1)

which involves the step size ℓ=8 nm of the kinesin motor and depends on the thermal energy given by Boltzmann constant k _B times temperature T. We use the convention that positive and negative load forces F or $\bar{F}$ correspond to resisting and assisting forces, respectively.

In general, these rates can be parametrized in the factorized form

$$ \omega_{ij}\equiv\omega_{ij,0} \varPhi_{ij}(F) \quad\mbox{with } \varPhi_{ij}(F = 0) \equiv1 $$

(2)

and

(3)

where the units of the rate constants $\hat{\kappa}_{ij}$ and κ _ij are given by s⁻¹ μM⁻¹ and s⁻¹, respectively.

The force dependence of the transition rates is described by the factor Φ _ij (F). For chemical transitions, these factors are taken to have the form

(4)

which involves the dimensionless parameter χ _ij and the characteristic force $\bar{F}_{ij}'= \ell F_{ij}'/(k_{B}T)$. For $\bar{F}_{ij}'=0$, the expression in (4) reduces to the force-dependent factors Φ _ij (F) as used in [8]. The parameter $\bar{F}_{ij}'$ represents a force threshold for the influence of the external force onto the corresponding chemical transition as in [43]. For the mechanical transitions, we take the exponential dependence

(5)

(6)

The force dependence of the chemical transition rates can be adjusted by the load distribution factors χ _ij , which are taken to satisfy χ _ij =χ _ji with 0≤χ _ij ≤1, and the dependence of the mechanical rates is governed by θ with 0≤θ≤1. A good description of the experimental single motor data is obtained, if one chooses two different values, $\bar{F}_{1}'$ and $\bar{F}_{2}'$, for the force thresholds with $\bar{F}_{12}' = \bar{F}_{21}' = \bar {F}_{45}' = \bar{F}_{54}' \equiv\bar{F}_{1}'$ for the ATP binding and ATP release transition and $\bar{F}_{ij}'\equiv\bar{F}_{2}'$ for all other chemical rates. Likewise, two different values, χ ₁ and χ ₂, were chosen for the load distribution factors with χ ₁₂=χ ₂₁=χ ₄₅=χ ₅₄≡χ ₁ for the ATP binding and ATP release transition and χ _ij ≡χ ₂ for all other chemical rates [8].

An important issue is the dissociation of the motor from the filament. First, it is plausible that the motor unbinds primarily from state i=7, in which both heads contain ADP and are therefore loosely bound to the filament [41]. The state of the unbound motor will be labeled by i=0. Thus, motor dissociation is described by the transition from state i=7 to state i=0 in Fig. 1 [8]. Second, the unbinding rate ω ₇₀ should depend on force since the motor will unbind faster if it experiences a load force as can be concluded from the load force dependence of the run length as observed experimentally [6]. The latter force dependence is roughly exponential in agreement with transition state or Kramers theory. Thus, we will use the parameterization

$$ \omega_{70}=\kappa_{70} \exp\bigl(|F|/F_D\bigr) $$

(7)

which depends on the detachment force F _D [9]. In the steady state, the overall unbinding rate ε _si of the single motor from the filament is then given by [8]

(8)

where $P^{\rm{st}}_{7}$ describes the load-dependent steady state probability for the motor to occupy state i=7. Note that ε _si is the steady state flux from state i=7 to state i=0. Furthermore, the time scale 1/ε _si is equal to the average waiting time until adsorption in state i=0 if we put the motor back into state i=7 immediately after it has arrived at state i=0, compare [44].

2.4 Motor Dynamics

The motor dynamics is now described by the probabilities P _i =P _i (t) to find the motor in state i at time t, corresponding to a continuous-time Markov process on the chemomechanical network in Fig. 1. In order to reach a steady state, we consider the limit of a large transition rate ω ₀₇, i.e., we put the motor immediately back into state i=7 as soon as it reaches state i=0. The time evolution of these probabilities is governed by the master equation

(9)

The steady state is characterized by time-independent probabilities $P_{i} = P^{\mathrm{st}}_{i}$ with $\frac{d}{dt} P^{\mathrm{st}}_{i} = 0$. One then has to solve a system of linear equations as provided by ∑ _j≠i [P _j ω _ji −P _i ω _ji ]=0 for i=1,2,…,7, either by linear algebra or by graph-theoretical methods. As a result, one finds that the steady state probabilities $P^{\mathrm{st}}_{i}$ can be expressed as ratios of two polynomials, which are multilinear in the transition rates ω _ij as defined by (2) and depend on the external load forces F≡F _ext [38]. The steady state probabilities $P^{\mathrm{st}}_{i}$ to find the motor in state i is shown in Fig. 2(a) as a function of the external force for saturating ATP as well as low ADP and P concentrations. For small forces below the stall force F=F _st=7.2 pN [6], the states 5,6 and 7 dominate, for large forces above the stall forces, the motor primarily visits the states 2 or 3 of the backward cycle. Because of the large ATP concentration, the states 1 and 4 are rarely occupied for all values of the external load force.

Fig. 2

(a) Steady state probabilities $P^{\mathrm{st}}_{i}$ to find a single motor in state i as a function of external force F _ext for saturating ATP concentration [ATP]=1 mM and low ADP and P concentrations [ADP]=[P]=10 μM (semi-logarithmic plot). For small F _ext, the motor prefers to visit the states 5,6 and 7 and to complete the forward dicycles $\mathcal{F}^{+}$ and $\mathcal{F}_{DD}^{+}$. The probabilities $P^{\mathrm{st}}_{2}$ and $P^{\mathrm{st}}_{3}$ increase with increasing force F _ext and the motor becomes more likely to complete the backward dicycle $\mathcal{B}^{+}$. Because of the large ATP concentration, the motor stays in the states 1 and 4 for a relatively short time, and the corresponding probabilities $P^{\mathrm{st}}_{1}$ and $P^{\mathrm{st}}_{4}$ are small for all values of F _ext. (b) Motor velocity as a function of the external load force: Comparison between network calculations (full lines) and experimental data as reported in [45] (circles)

Using the steady state probabilities $P^{\mathrm{st}}_{i}$, we can calculate motor properties such as the motor velocity which is given by the excess flux along the |25〉 transition and, thus, by [8]

(10)

with the step size ℓ=8 nm as before. Note that both the mechanical transition rates ω ₂₅ and ω ₅₂ as well as the steady state probabilities $P^{\mathrm {st}}_{2}$ and $P^{\mathrm{st}}_{5}$ depend on the load force F _ext. Figure 2(a) shows that $P^{\mathrm{st}}_{2}$ strongly increases with increasing F _ext up to the stall force and then saturates for superstall forces. In contrast, the probability $P^{\mathrm{st}}_{5}$ is essentially constant for substall forces and strongly decays for superstall forces.

The motor velocity as a function of the external load force is shown in Fig. 2(b) for both large and small ATP concentration in good agreement with the experimental data in [45]. We use the transition rate constants derived in [8] except for the ATP binding rate $\hat{\kappa}_{12}$, the ADP release rate κ ₅₆ and the rate of the alternative pathway κ ₅₇=κ ₅₆/2. These latter rates were adjusted to the experimental data in [45]. For saturating ATP concentration, the motor velocity is proportional to ω ₅₆ whereas for small ATP concentration the limiting rate is the ATP binding rate ω ₁₂. As a result of this procedure, we found the parameter values as given in Table 1.

Table 1 Transition rate constants for the network in Fig. 1 adjusted to data in [45]; ^∗ value adopted from [8]; ^† value via balance conditions, see [40], such as $\hat{\kappa} _{65} = \hat{\kappa}_{12} \kappa_{25} \kappa_{56} \kappa _{61}/(\kappa_{21} \kappa_{52} K_{\mathrm{eq}} \hat{\kappa}_{16})$, with K _eq as found in [46] and with k _B T=4 pN nm at room temperature. The rate constants of the backward cycle are identified with the rates of the forward cycle, except κ ₅₄, which is determined by the balance condition; ^‡ value calculated via (8) and (26), respectively, using experimental data as explained below in Sect. 4.2. All rate constants κ _ij are given in units of 1/s, all rate constants ${\hat{\kappa}}_{ij}$ in units of 1/(μM s). Force factors are adjusted for the data in [45], detachment force F _D from [9], stall force F _st as measured in [6]. In addition to the single motor parameters displayed in this table, our theory involves only two parameters, the elastic coupling parameter K and the single motor rebinding rate $\pi_{\rm si}$, both of which can be deduced from the motor and cargo trajectories, see Sect. 8 below

Both force velocity curves decrease with increasing load force and vanish at the stall force F _st=7.2 pN. Inspection of Fig. 2(b) shows that, for saturating ATP concentration the motor velocity is hardly affected by assisting forces, i.e., by pulling the motor in the direction of motion, while for small ATP concentration the velocity already starts to decrease at small assisting forces. The single motor velocity v _si can be experimentally determined by measuring the average run length 〈x _si〉 and the average run time 〈t _si〉 of a single motor run. The single motor run time 〈t _si〉 is related to the overall unbinding rate ε _si via 〈t _si〉=1/ε _si and depends on the nucleotide concentrations, since the rate ε _si as defined in (8) depends on these concentrations via the steady state probability $P^{\mathrm {st}}_{7}$ for state 7. As explained above, the steady state probabilities $P^{\mathrm {st}}_{i}$ can be expressed as ratios of two polynomials, which are multilinear in the transition rates ω _ij as defined by (2). The single motor run time 〈t _si〉 as a function of the ATP-concentration is shown in Fig. 3. At small ATP-concentrations, the single motor run time is 〈t _si〉=1.84 s and decreases to 〈t _si〉=1.52 s at saturating ATP-concentrations for fixed concentrations of the hydrolysis products, [ADP]=[P]=10 μM.

Fig. 3

Average run time 〈t _si〉 of a single motor as a function of the ATP concentration (semi-logarithmic plot). The concentration of the hydrolysis products has been set to [ADP]=[P]=10 μM. The red data point represents the average value 〈t _si〉=(1.54±0.03) s, as calculated from the experimental data in [45] via 〈t _si〉=〈x _si〉/v _si

3 Coupled Motors

In order to obtain a detailed description for a pair of coupled motors, we describe each motor by its chemomechanical network and couple these two motors and, thus, the two networks by an elastic spring. Because of the elastic strain forces mediated by this spring, mechanical steps by one motor influence the transition rates of both motors if they are both connected to the filament. The elastic coupling may lead to interference effects: the two motors may stall each other or one motor may pull the other motor from the filament. However, we also expect a motor pair to cover larger distances compared to a single motor since a detached motor is still close to the filament and hence is able to rebind to the filament before the other motor detaches as well.

3.1 Theoretical Description

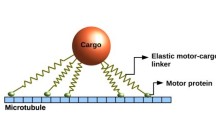
The motor system considered here consists of two kinesin motors which are attached to the same bead or cargo and walk on the same microtubule as indicated in the top row of Fig. 4. Because the stalk of the kinesin molecule is flexible, we consider this stalk to behave as a harmonic spring with spring constant κ and focus on the spring extensions parallel to the filament. The corresponding rest length L _∥ will be of the order of the stalk length, which is about 80 nm, if the separation between the cargo and the filament is about (17 ± 2) nm as observed in [47]. All our results as described below were obtained for L _∥=80 nm. The mutual interaction forces that the two motors and the cargo experience parallel to the filament are then described by two linear, harmonic springs attached to the bead or cargo as indicated in the middle row of Fig. 4.

Fig. 4

(Top row) Overall cargo run for two kinesin motors (blue), each of which has two motor heads. Both motors are attached to the same cargo (light gray) and walk along the same filament (black line); (Middle row) Reduced representation of the overall cargo run in terms of three ‘particles’ corresponding to the leading motor at position x _le, the trailing motor at position x _tr, and the cargo with center-of-mass position x _ca. These three ‘particles’ are connected via two linear springs with spring constant κ and rest length L _∥. (Bottom row) Reduced representation of the overall cargo run in terms of only two motor ‘particles’ connected by a single spring. As long as both motors are attached to the filament and, thus, active as indicated by the blue ‘balls’ they perform a 2-motor run, during which each mechanical step of one motor affects, via the elastic spring, the force experienced by both motors. After unbinding from the filament, an active motor becomes inactive as indicated by the white ‘balls’. If the cargo is pulled by only one active motor, the cargo performs a 1-motor run until (i) it either unbinds as well, leading to an unbound motor pair, or (ii) the inactive motor rebinds to the filament and the cargo starts another 2-motor run. We will denote the distances and times traveled during 2-motor runs by Δx ₂ and Δt ₂ and those during 1-motor runs by Δx ₁ and Δt ₁. Here and below, all quantities that refer to 1-motor and 2-motor runs will be labeled by subscript 1 and 2, respectively. Unbound cargo states, in which both motors are inactive, will be indicated by the subscript 0. We do not take diffusion of the unbound cargo state into account

The leading motor, which walks in front of the other motor, has position x _le on the filament and its states are labeled by i=i _le. Likewise, the trailing motor is located at position x _tr with states labeled by i=i _tr. The stalks of the two motors are anchored at the surface of the rigid bead or cargo. The distance between the two anchor points is assumed to be fixed in order to ensure that the motors do not interact sterically. As long as both motors are attached to the filament, we also preserve the ordering of the two motors with respect to the filament, i.e., the motors are not allowed to pass each other. In general, a reordering of motors is possible during 1-motor runs. Thus, rebinding of the detached motor may occur either in front or behind the active motor if we include the possibility that the cargo rotates during the 1-motor runs and the trailing and leading motors are interchanged. The rotational diffusion constant for a spherical particle with radius R in water is given by

(11)

at room temperature. Then, a rotation of the bead by π or 180° leads to a typical time scale t _rot with

(12)

which implies

(13)

which has to be compared to the run time of 1-motor runs. Typically, a single motor run takes only a few seconds [13]. As we will see in Sect. 3.3, the run time of a 1-motor run is always short compared to the run time of a single motor. For bead radii that are larger than 350 nm the expression in (13) exceeds the single motor run time. In the following, we will focus on relatively large beads, for which appreciable cargo rotation and, thus, interchange of the trailing and leading motor can be neglected.

3.1.1 Force Balance During 2-Motor Runs

Since each motor can unbind from and rebind to the filament, the cargo can be actively pulled by one, two or no motors corresponding to three different activity states. If both motors provide a connection between the cargo and the filament, the cargo performs a 2-motor run. During such a run, the cargo with center-of-mass position x _ca is subject to two forces arising from the two motors. The force that the leading motor exerts onto the cargo is given by

(14)

which is positive if x _le−x _ca>L _∥, i.e., if the leading spring pulls in the positive x-direction. Likewise, the force that the trailing motor exerts onto the cargo is

(15)

We now assume that, for given positions x _le and x _tr of the two motors, the elastic forces balance each other on time scales that are small compared to the time scales of the single motor transitions. This assumption allows us to eliminate the cargo position from the theory, as indicated in the bottom row of Fig. 4. Elastic force balance implies F _le,ca+F _tr,ca=0 or the average cargo position

(16)

Thus, after the forces have balanced, both springs have the same spring extension and the actual length of each spring is given by

(17)

and the elastic force acting on the leading motor is equal to

(18)

with effective spring parameters

(19)

Thus, a stretched spring with $x_{\mathrm{le}}- \bar{x}_{\mathrm{ca}}> L_{\parallel}$ generates a force F _ca,le<0 acting in the negative x-direction. Likewise, the elastic force acting on the trailing motor is given by

(20)

Since the elastic forces depend only on the spring extension

(21)

which represents the deviation of the actual spring length from its rest length and, thus, the deviation of the actual motor-motor separation from its relaxed value, the leading motor exerts the interaction force

(22)

onto the trailing motor, which exerts the force

(23)

on the leading motor as required by Newton’s third law. In this way, we obtain a reduced description of the motor pair in terms of two kinesin motors connected via a single linear spring with the coupling parameter K=κ/2 and the effective rest length L ₀=2L _∥.

If we focus on one of the two motors during a 2-motor run, the elastic force (23) may be regarded as a load force acting on this motor, which thus enters its force-dependent transition rates in (2) and its force-dependent unbinding rate in (8). In these latter relations, we used the convention that resisting forces are positive, whereas assisting forces are negative. Therefore, the forces that enter these relations are F=F _le with

(24)

and F=F _tr with

(25)

Thus, the leading motor experiences a resisting force F _le>0 if the trailing motor is subject to an assisting force F _tr<0 and vice versa, as required by Newton’s third law.

3.1.2 Transitions Between 2-Motor and 1-Motor Runs

Now, consider a 2-motor run and assume that one of the two motors visits its single motor state 7, which is loosely bound to the filament, see Fig. 1. This motor then unbinds from the filament with transition rate ω ₇₀, which transforms the 2-motor run into a 1-motor run by the other motor, which is still bound to the filament, see Fig. 4. The latter motor now pulls both the cargo and the detached motor along with it. During such a 1-motor run, mechanical equilibrium between the elastic forces acting on the cargo implies that the two linear springs are relaxed and that ΔL=0. The detached motor is still connected to the cargo and, thus, remains close to the filament. When this motor rebinds to the filament, the 1-motor run is terminated and another 2-motor run begins.

We will ignore chemical transitions of the unbound motor, which implies that motor rebinding to the filament only occurs back to the single motor state i=7, and assume force independent rebinding. The corresponding rebinding rate will be denoted by

(26)

Furthermore, since the 1-motor runs are characterized by ΔL=0, rebinding of a detached motor initially leads to a state with ΔL=0 as well, corresponding to no elastic force between the two bound motors. Such a force is generated as soon as one of the motors performs a mechanical step which leads to a stretching or compression of the effective spring between the two motors.

When bound to the filament, the motors are active and undergo their chemomechanical cycles. During a 1-motor run, the actively pulling motor exhibits the same properties as a single motor. The latter properties have been studied in great detail and are taken into account here via the detailed chemomechanical network description. The average run length and run time of a 1-motor run are, however, shorter than the corresponding quantities of a single motor since the 1-motor runs may be terminated by the rebinding of the second motor.

During a 2-motor run, on the other hand, both motors undergo their individual chemomechanical cycles but, at the same time, experience the mutual interaction force (23), which depends on the extension ΔL of the motor-motor separation from its rest length L ₀. Whenever one of the two motor performs a mechanical step, this step changes the extension ΔL and, thus, the mutual interaction force. Since this force enters all transitions of both motors, a single mechanical step affects all subsequent transitions of both motors. This feedback mechanism between mechanics and chemistry represents the most important aspect of the system considered here.

As explained in the following subsections, we will construct a network representation for the motor pair that is based on a combination of the chemomechanical networks for the two individual motors. In this way, we obtain a unique representation of the state space for the motor pair. Furthermore, we take all transitions between these motor pair states into account that arise from transitions of individual motors. Simultaneous transitions of both motors, on the other hand, will not be considered since the motor dynamics will be described as a continuous-time Markov process. For such a process, the probability that a single motor transition occurs during a small time interval of size dt is proportional to dt. Therefore, the probability for simultaneous transitions of both motors is proportional to dt ² and, thus, of higher order in dt.

As explained before, a motor performing a mechanical step exerts an interaction force onto the other motor and then feels the corresponding reactive force as in (23). As long as these forces are small, each motor will essentially behave as a single, noninteracting motor, and the probability distribution for its single motor states will then be close to the one displayed in Fig. 2(a). On the other hand, if these forces become sufficiently large compared to the motors’ detachment force, either by a large extension ΔL of the motor-motor separation or by a strong elastic coupling, the interactions are no longer negligible and will lead to a variety of interference effects as recently categorized in [25].

3.2 Network Representation of Motor Pair

In order to address the stochastic behavior of a motor pair consisting of two identical kinesin motors, we describe each motor by a single motor network as depicted in Fig. 1. A motor pair state a is now defined by the single motor states i=i _le and i=i _tr of the leading and the trailing motors as well as by the extension ΔL of the motor-motor separation L from its rest length L ₀. In this way, we generate a new state space for the motor pair as shown in Fig. 5(a).

Fig. 5

State space of motor pair as described by three coordinates: the motor states i _le of the leading motor (horizontal axis), the motor states i _tr of the trailing motor (vertical axis), and the extension ΔL of the elastic spring (axis perpendicular to the plane of the figure). The motor pair states form a stack of layers, each of which corresponds to a fixed value of ΔL in units of the stepsize ℓ. (a) Single layer of state space with ΔL=0. Open circles represent motor pair states with ΔL=0, gray lines represent the chemical transitions between these states. Full green stubs describe mechanical forward steps of the leading motor, emanating from a state (2,i _tr;0) and reaching a state (5,i _tr;1) in the overlying layer with ΔL=1. Broken green stubs describe mechanical backward steps of the leading motor, emanating from a state (5,i _tr;0) and reaching a state (2,i _tr;−1) in the underlying layer with ΔL=−1. Likewise, the full and broken blue stubs describe forward and backward steps of the trailing motor. Red lines represent binding and unbinding events between the single motor states i=7 and i=0. When a motor unbinds from a state (7,i _tr;ΔL) with ΔL≠0, it reaches a state (0,i _tr;0) with ΔL=0. The unbound motor pair is described by the pair state (0,0;0) in the upper right corner. (b) Stack of five layers: the layer with ΔL=0 is colored in red, the two layers with ΔL=±1 in dark grey, and the two layers with ΔL=±2 in light grey. Each layer is connected to two boundary lines, which are defined by the motor pair states (i _le,0;0) along the i _le-axis and by the states (0,i _tr;0) along the i _tr-axis. All of these latter states represent 1-motor runs whereas all other motor pair states within the different layers represent 2-motor runs. The unbinding transitions from 2-motor run states with ΔL>0 and ΔL<0 to 1-motor run states with ΔL=0 are described by the full and broken black lines, respectively. The red lines represent both the unbinding transitions from 2-motor run states with ΔL=0 to 1-motor run states as well as the rebinding transitions from 1-motor run states to 2-motor run states with ΔL=0. Red arrows represent transitions to the unbound state of the motor pair

As explained before, 1-motor runs are characterized by ΔL=0 corresponding to a relaxed elastic coupling between the two motors. The motor pair in state a=(i _le,i _tr;ΔL) may undergo transitions to all neighboring states b according to

(27)

(28)

The corresponding transition rates will be denoted by ω _ab . In general, ΔL′=ΔL for all chemical transitions, but ΔL′≠ΔL for all mechanical transitions. It is important to realize that, for the continuous-time Markov process considered here, each transition rate ω _ab can be identified with a single motor rate as given by

(29)

(30)

which has the same form as expression (2) where F _le and F _tr represent the forces experienced by the leading and the trailing motors as introduced in (24) and (25).

As shown in Fig. 5(b), the motor pair states form a stack of layers, each of which is characterized by a constant value of ΔL. The layer with ΔL=0, see Fig. 5(a), is special since it contains the unbound motor state (i _le,i _tr;ΔL)=(0,0;0) as well as two boundary lines. The first boundary line is defined by motor pair states

(31)

and represents 1-motor runs of the leading motor. The second boundary line is defined by the states

(32)

and represents 1-motor runs of the trailing motor. Each of these boundary lines represents a copy of the single motor network depicted in Fig. 1. Any 1-motor run may be terminated in two ways: (i) by unbinding of the active motor, which leads to the unbound motor pair state (i _le,i _tr;ΔL)=(0,0;0), or (ii) by rebinding of the inactive motor back to the filament. Rebinding of the inactive trailing motor leads from state (i _le,i _tr;ΔL)=(i,0;0) to state (i _le,i _tr;ΔL)=(i,7;0) whereas rebinding of the inactive leading motor leads from state (i _le,i _tr;ΔL)=(0,i;0) to state (i _le,i _tr;ΔL)=(7,i;0), see Fig. 5. All of these rebinding transitions are governed by the rebinding rate π _si as in (26).

The unbound motor pair is described by the pair state (i _le,i _tr;ΔL)=(0,0;0) in the upper right corner of Fig. 5(a). In general, a motor pair run is terminated after arriving in this state. However, as far as the unbound state is concerned, the cargo is assumed to stay at the position, at which it became completely detached from the filament and the position of the instantly rebinding motor is calculated with respect to this cargo position. This procedure provides long trajectories of the motor pair.

Mechanical steps during 2-motor runs lead to transitions between neighboring ΔL-layers as indicated by the blue and green stubs in Fig. 5(a). These stubs emanate from motor pair states, for which one of the two motors dwells in the single motor state i=2 or i=5, compare Fig. 1. The transitions between 2-motor and 1-motor runs are provided by binding and unbinding events that are indicated by red lines and black stubs in Fig. 5(a) and by red and black lines in Fig. 5(b). Unbinding of one motor from a pair state with ΔL≠0 corresponds to a transition back to a pair state with ΔL=0 and either i _le=0 or i _tr=0 since the extension ΔL is taken to vanish in a 1-motor run. As explained before, the extension ΔL continues to vanish directly after a rebinding event, i.e., directly after a transition that emanates from the two boundary lines.

Since the state space for a motor pair as described above is hardly amenable to analytical calculations, we will study it by stochastic simulations as described below in Sect. 4. It is important to note, however, that our description of the motor pair system, which is based on the motor cycles of a single motor, involves only two additional parameters, the coupling parameter K as well as the single motor rebinding rate π _si, and only one new state variable, the extension ΔL of the motor-motor separation.

3.3 Activity States of the Motor Pair

As previously mentioned, the network in Fig. 5 can be decomposed into three parts corresponding to three distinct activity states: (i) The unbound state with (i _le,i _tr;ΔL)=(0,0;0), in which both motors are inactive, (ii) the two boundary lines as defined by (31) and (32), corresponding to 1-motor runs with one active and one inactive motor; and (iii) the remaining stacked layers of states, which represent 2-motor runs with two active motors. As shown in Fig. 5, each layer is characterized by a fixed value of the extension ΔL of the motor-motor separation and consists of 7²=49 states for 2-motor runs. The extension ΔL determines the elastic interaction force between the two motors. This interaction force changes as soon as one of the motors performs a mechanical step, which leads to a transition to the neighboring ΔL layer. Mechanical forward steps of the leading motor and mechanical backward steps of the trailing motor increase the extension from ΔL to ΔL+ℓ whereas backward steps of the leading motors and forward steps of the trailing motor decrease the extension from ΔL to ΔL−ℓ, as indicated by the blue and green stubs in Fig. 5(a). Thus, mechanical steps during 2-motor runs lead to transitions parallel to the ΔL axis of the state space while chemical transitions connect two motor pair states within the same ΔL layer.

4 Simulation Method

For the single motor network in Fig. 1, we calculate the steady state solution as the nullspace of the transition matrix of the Master equation in (9), see, e.g., [48]. Since the state space for a motor pair as described in Fig. 5 is hardly amenable to analytical calculations, we use the Gillespie algorithm [49] to generate random walks on the motor pair network. This algorithm is exact apart from numerical round-off errors. As previously mentioned in Sect. 3.2, transitions between the motor pair state a=(i _le,i _tr;ΔL) and the motor pair state b=(j _le,i _tr;ΔL′) for the leading motor or b=(i _le,j _tr;ΔL′) for the trailing motor respectively, are governed by single motor transition rates $\omega_{ab}=\omega_{ij,\rm{le}}$ or $\omega_{ab}=\omega_{ij,\rm{tr}}$ respectively as in expression (29) and (30).

Then we can define the average dwell time 〈τ _a 〉=1/∑ _b ω _ab for the pair state a=(i _le,i _tr;ΔL) and transition probabilities Π _ab =ω _ab 〈τ _a 〉 from pair state a=(i _le,i _tr;ΔL) to pair state $b=(i_{\mathrm{le}}', i_{\mathrm{tr}}; \Delta L')$ or $b=(i_{\mathrm{le}}, i_{\mathrm{tr}}'; \Delta L')$ respectively. These transition probabilities are normalized with ∑ _b Π _ab =1 for all motor pair states a. Note that the average dwell times 〈τ _a 〉 are related to the average dwell times of the single motors via

(33)

with $\langle\tau_{i_{\mathrm{le}}} \rangle=1/\sum_{j} \omega _{ij,\mathrm{le}}$ and $\langle \tau_{i_{\mathrm{tr}}} \rangle=1/\sum_{j} \omega_{ij,\mathrm{tr}}$ respectively, depending on the single motor transition rates of each motor. Thus, for a motor pair state a that belongs to a 1-motor run, the average dwell time 〈τ _a 〉 is affected by the inactive motor, which may rebind to the filament.

4.1 Procedure for Generating Motor Pair Walks

In order to generate the random walks on the motor pair network in Fig. 5, we used the following procedure:

• (i) Start at time t=0 in state a=(i _le,0;0) corresponding to an unbound trailing motor and a bound leading motor in motor state i _le=7. As explained in Sect. 3.1.2, the motor pair attains this state directly after the rebinding of the leading motor to the filament.

• (ii) Choose a random dwell time τ _a for state a. Since the dwell times τ _a are taken to be exponentially distributed, a random number r _τ is chosen with uniform probability density over the interval 0<r _τ <1, from which the random dwell time τ _a is calculated via τ _a =−〈τ _a 〉ln(r _τ ).

  Choose a random number 0≤r _Π ≤1 to determine the transition event e. Assign intervals of size Π _ab to each state b which is connected to a and compare r _Π successively to these intervals. If r _Π lies within an interval, accept the transition to the new state b, otherwise reject it.

• (iii) Update the clock time t _e−1 to t _e =t _e−1+τ _a , calculate the position of the cargo $x_{\rm{ca}}$, the extension ΔL of the motor-motor separation and the effective forces F _le and F _tr. Update the transition rates, mean dwell times in the new state b and transition probabilities out of this state, and record required quantities.

  Note, that the position of the cargo could be a float, whereas the position of the motors on the filament has to be an integer, since the binding sites on the filament are discrete with the lattice constant of ℓ=8 nm. The position of the inactive motor during a 1-motor run is identified with the position of the cargo. When the transition event e is an rebinding event of the inactive motor, calculate the new position of this motor on the filament in respect to the cargo as described in (16). If the calculated new position on the filament lies between two binding sites, choose one of these binding sites with probability $\frac{1}{2}$. For L _∥=80 nm as used here, the latter rule becomes only effective in the presence of an external force, which will be studied elsewhere.

Repeat step (ii) and (iii). Last step: Stop the walk at time t _max. Note that t _max should be sufficiently large compared to the time required to complete a cycle $\mathcal{C}_{\nu}$ of the single motor network.

In principle, a motor pair walk is terminated after it arrives in state a=(0,0;0), i.e., when no motor is bound to the filament. It is, however, more convenient to continue the motor pair walk by immediately rebinding one of the motors where each motor is chosen with probability $\frac{1}{2}$. The cargo is assumed to stay at the position, at which it became completely detached and the position of the instantly rebinding motor is calculated with respect to this cargo position. In this way, we replace an ensemble average over many relatively short walks by a time average over one relatively long walk. For computational reasons, each of these long walks is stopped after t _max≃10⁴ s; the simulation time has been chosen in such a way that the cargo performs approximately 10⁶ steps in the force free case.

4.2 Specification of Parameters

The overall unbinding rate ε _si for zero external load force as given by (8) with F=0 has been determined from the experimental data in [45] for the single motor runlength 〈x _si〉=(1.03±0.17) μm and velocity v _si=(668±8) nm/s at saturating ATP-concentration. As a result, we found ε _si≃v _si/〈x _si〉≃0.65/s. Inserting this value of ε _si together with the calculated probability $P^{\mathrm{st}}_{7}$ into expression (8) with F=0 we determine the rate constant κ ₇₀. We choose the single motor rebinding rate π _si=5/s as found in [30] unless noted otherwise.

We will study the coupling parameter K=κ/2 of the assembly in the following range: We refer to the largest elastic modulus found in [50] for AMP-PNP governed kinesin heads with κ≃0.92 pN/nm and therefore limit our calculations to K≤0.5 pN/nm. We choose K≥0.02 pN/nm, since smaller values of K are not convenient: for K<0.02 pN/nm, the extension of the motor-motor separation ΔL>160 nm gets large compared to the size of the assembly. These arguments lead to the range 0.02≤K [pN/nm]≤0.5 for the coupling parameter K with a weak coupling regime K≳0.02 pN/nm and a strong coupling regime with K≲0.5 pN/nm.

The system is typically set up at zero external load force and at saturating ATP concentration [ATP]=1.6 mM and small ADP and P concentrations [ADP]=[P]=10 μM unless noted otherwise.

4.3 Vanishing Unbinding or Rebinding Rate

The transport properties of single motors can be reproduced by disabling rebinding transitions in order to check the algorithm. The starting state in step (i) is then chosen according to the probability distribution as shown in Fig. 2(a). On the other hand, by disabling unbinding transitions, we obtain long 2-motor runs and therefore a better statistics for certain properties of these runs such as the distribution for ΔL. In the latter case, we start with two active motors with ΔL=0 in step (i). The individual initial states of the two motors are chosen according to the single motor probability distribution as shown in Fig. 2(a).

5 Dwell Times Between Individual Cargo Steps

For gliding assays, in which the motors are immobilized on a substrate surface, it is possible to distinguish 4 nm and 8 nm steps of the filaments which permits to distinguish between 1-motor run and 2-motor run regions as shown in [33]. For bead assays as considered here, one could perform analogous experiments, in particular if one uses two different fluorescent labels for the two motors, a method that has been recently applied to the two heads of a single dynein motor [39], to two different myosin motors [51] and to two identical coupled myosin V motors [52]. A time resolution in the range of ms would then allow to measure the different run times during a motor pair run and to detect the dwell times between individual steps even at saturating ATP concentrations.

The overall cargo trajectory displayed in Fig. 6(a) consists of two segments. During the first 55 ms, the cargo performs a 1-motor run with 8 nm displacements. At 55 ms, the other motor rebinds and the cargo undergoes a 2-motor run with 4 nm displacements, in close analogy to the experimental results in [33]. Therefore, calculating the average cargo position via the relation (16) shows that a cargo transported by two motors is displaced by 4 nm when one of the motors makes a 8 nm step. The cargo trajectory in Fig. 6(a) is labeled by the dwell times between two steps. The unlabeled part of the trajectory in the middle of the plot represents the switch region between the 1-motor and the 2-motor run, i.e., the dwell time between the last mechanical step during the 1-motor run and the rebinding event. For the histogram in Fig. 6(b), we count only dwell times between two mechanical steps. In general, a transition from a 1-motor to a 2-motor run is defined by a 8 nm step followed by a 4 nm step in the cargo trajectory or vice versa. Inspection of Fig. 6(a) indicates that the dwell times Δτ ₂ between two cargo steps during a 2-motor run are smaller than the dwell times Δτ ₁ during a 1-motor run.

Fig. 6

(a) Cargo trajectory of a motor pair system with a coupling parameter of K=0.02 pN/nm for zero external force. Cargo steps during a 2-motor run are marked by red color. During the 1-motor run the cargo moves by 8 nm steps whereas it performs 4 nm steps during a 2-motor run. The trajectory is labeled by the dwell times (in units of ms) between two successive cargo steps. The unlabeled segment of the trajectory represents the transition from the 1-motor run to the 2-motor run via a rebinding event. (b) Relative frequency count of the dwell times between two steps of the cargo trajectory. Red bars describe the dwell time distribution of 2-motor runs, black bars the dwell time distribution of 1-motor runs. The average dwell times between two cargo steps are found to be 〈Δτ ₁〉=(11.6±0.1) ms for 1-motor runs and 〈Δτ ₂〉=(6.02±0.02) ms for 2-motor runs

The dwell time distributions in Fig. 6(b) which are derived by stochastic simulations of rather long trajectories, confirm this inequality. If the interactions between the two motors can be neglected, one has a 2-motor run stepping rate that is twice the single motor stepping rate [53]. The average stepping rate 1/〈Δτ ₂〉=(166.1±0.6)/s of the 2-motor run for weak coupling with K=0.02 pN/nm in Fig. 6 is almost twice as big as the 1-motor run stepping rate 1/〈Δτ ₁〉=(86.2±0.7)/s. The latter value corresponds to the inverse of the completion time for the forward cycle $\mathcal{F}$ and is in good agreement with the experimental value v _si/(8 nm)=(83.5±1.0)/s for single kinesin motors with v _si=(668±8) nm/s as found in [45].

6 Average Run Times for 1- and 2-Motor Runs

As previously mentioned, the distances and times traveled during 2-motor runs are denoted by Δx ₂ and Δt ₂ and those during 1-motor runs by Δx ₁ and Δt ₁. Each of these quantities represents a stochastic variable that is governed by a certain probability distribution $\mathcal{P}$ that can be determined by stochastic simulations. We then define the average run length of 1-motor and 2-motor runs by

(34)

and the average run times for these runs by

(35)

The average velocities of the 1-motor and 2-motor runs are given by

(36)

In general, 1-motor runs may be terminated in two ways: First, the active motor may unbind from the filament as well, which implies a transition from the state a=(7,0;0) to the unbound state b=(0,0;0). The corresponding transition rate ω _ab is equal to the single motor unbinding rate ω ₇₀. Second, the nonactive motor may rebind to the filament, which leads to transitions from the motor pair states a′=(i,0;0) to the states b′=(i,7;0), see Fig. 5. These rebinding events are all governed by the same transition rate ω _a′b′=π _si. Therefore, the average run length 〈Δx ₁〉 as well as the average run time 〈Δt ₁〉 of 1-motor runs is smaller than the average run length 〈x _si〉 and run time 〈t _si〉 of a single motor. The average velocity v ₁, on the other hand, is equal to the average velocity v _si of a single motor. Inspection of Fig. 7 shows that the average run time 〈Δt ₁〉 of 1-motor runs is given by

(37)

with the overall unbinding rate ε _si=1/〈t _si〉 and the rebinding rate π _si of a single motor. This relation implies 〈Δt ₁〉<1/(2ε _si) as long as ε _si<π _si.

Fig. 7

Three activity states α=0, 1 and 2 of a cargo corresponding to its unbound state, 1-motor runs, and 2-motor runs, respectively. The transition |10〉 with the rate ε _si corresponds to the unbinding of the active motor, the transition |12〉 with rate π _si to the rebinding of the inactive motor, and the transition |21〉 with rate ε ₂ to the unbinding of one of the two active motors

A 2-motor run is terminated by the unbinding of one of the two active motors. The overall rate for this process will be denoted by

(38)

as indicated in Fig. 7. If the interactions between the two motors can be neglected, one has [53]

(39)

On the other hand, if the motors exert the elastic forces ±KΔL onto each other, the termination rate ε ₂ of the 2-motor runs will be affected by interference effects arising from these motor-motor interactions [25].

The cargo trajectories of two motor pairs in two different transport regimes, a weakly coupled motor pair with the K=0.02 pN/nm and a strongly coupled one with K=0.5 pN/nm, are compared in Fig. 8(a), 2-motor runs are marked in red and blue. The different slopes of the two trajectories depicted in Fig. 8(a) reflect the general property that the average cargo velocity decreases with an increasing coupling parameter.

Fig. 8

(a) Cargo trajectories for two different transport regimes: weak coupling with K=0.02 pN/nm (red/black) and strong coupling with K=0.5 pN/nm (blue/black). Cargo steps during 2-motor runs are marked in red for weak coupling and in blue for strong coupling. 1-motor runs are in black. (b) Run time distributions $\mathcal{P}_{1,t}(\Delta t_{1})$ of 1-motor runs and $\mathcal{P}_{2,t}(\Delta t_{2})$ of 2-motor runs for two different coupling parameters K. The distributions of 1-motor runs should not depend on the coupling parameter as confirmed by the unshaded and shaded bars that represent the data for K=0.02 pN/nm (weak coupling) and K=0.5 pN/nm (strong coupling) respectively. Lines with symbols describe the distribution of the 2-motor run times for weak coupling (red squares) and strong coupling (blue circles). The broad run time distribution for 2-motor runs in the weak coupling regime leads to the average run time 〈Δt ₂〉=(616±5) ms, which is more than twice the corresponding value 〈Δt ₂〉=(239±2) ms in the strong coupling regime. The run time distributions for the 1-motor runs as obtained from both trajectories are in good agreement with each other and imply 〈Δt ₁〉=(178±2) ms and 〈Δt ₁〉=(178±1) ms, respectively, which should be compared with 〈Δt ₁〉=177 ms as derived from (37)

The run time distributions $\mathcal{P}_{1,t}(\Delta t_{1})$ during 1-motor runs and $\mathcal{P}_{2,t}(\Delta t_{2})$ 2-motor runs for the two different motor pairs are shown in Fig. 8(b). The broad run time distribution for 2-motor runs in the weak coupling regime implies an average value 〈Δt ₂〉 that is more than twice the corresponding value in the strong coupling regime. Thus, weak coupled motor pairs spend more time in a 2-motor run than strong coupled motor pairs. The run time distributions for the 1-motor runs are essentially identical for both coupling parameter. The average value 〈Δt ₁〉 as deduced from the trajectories is in good agreement with the value obtained via the expression (37).

As mentioned before, the average run time 〈Δt ₂〉 determines the termination rate ε ₂=1/〈Δt ₂〉 of the 2-motor runs. The average values for the 2-motor run times in Fig. 8(b) imply ε ₂=(1.62±0.01)/s for weak coupling and ε ₂=(4.18±0.04)/s for strong coupling and lead to the ratios in Table 2. Therefore, the termination rate ε ₂ of 2-motor runs increases with increasing coupling parameter K as experimentally observed in a recent experimental study [32].

Table 2 Ratio of the termination rate ε ₂ of the 2-motor runs to the overall unbinding rate ε _si of single motors for different coupling parameter K. The termination rate ε ₂ of the 2-motor runs is determined by (39) for the non interacting motors with K=0 and by (38) for the 2-motor run times in Fig. 8(b) as well as for K=0.1 pN/nm

7 Relative Frequency of 1- and 2-Motor Runs

A cargo run consists of alternating 1- and 2-motor runs, which represent the activity states α=1 and α=2 in Fig. 7 and a final 1-motor run ending in activity state α=0. A motor pair walk consists of several cargo runs, separated by the activity state α=0. As explained in Sect. 4.1, once the motor pair reaches the activity state α=0, it is immediately returned to α=1 by rebinding one of the two motors back to the filament. This protocol is used in order to replace an ensemble average over many short walks by a time average over one long walk.

Since the excursions of the motor pair walk to the activity state α=0 take no time, the probability $\mathcal{P}_{\alpha}$ to find the motor pair in activity state α during a motor pair walk is determined by

(40)

according to the reduced description in Fig. 7, which implies

(41)

where the latter equality follows from (38). Each cargo run starts with a 1-motor run and ends with a 1-motor run, the average number 〈n ₁〉 of 1-motor runs and the average number 〈n ₂〉 of 2-motor runs in a cargo run are simply related via

(42)

and imply the average cargo run time 〈Δt _ca〉

(43)

As mentioned before, the average run time 〈Δt ₁〉 is related to the single motor rates π _si and ε _si as in (37) and 〈Δt ₂〉≡1/ε ₂ as in (38). Inserting these relations into (43), we obtain

(44)

On the other hand, the average cargo run time can be interpreted as the average waiting time for the cargo run to be absorbed in state α=0, which is given by the inverse probability flux from the activity state α=1 to the absorbing state α=0, compare [44], i.e., by

(45)

A combination of this latter relation with (44) and (40) leads to the average numbers

(46)

and

(47)

where the last equality follows from (37).These relations imply that the average numbers of 1-motor runs and 2-motor runs in a cargo run do not depend on the coupling parameter K, but only on the rebinding rate π _si. For the limiting case π _si=0, i.e., if we inhibit motor rebinding, the relations (46) and (47) lead to 〈n ₂〉=0 and 〈n ₁〉=1, i.e. the cargo run consists of a single 1-motor run. Furthermore, it follows from (41), (46) and (47) that

(48)

Since the average numbers 〈n ₁〉 and 〈n ₂〉 of 1-motor and 2-motor runs as well as the average run times 〈Δt _α 〉 are accessible to our simulations, we can determine the probability ratio $\mathcal{P}_{2}/\mathcal{P}_{1}$ via (48).

The ratio $\mathcal{P}_{2}/\mathcal{P}_{1}$ is shown in Fig. 9(a) as a function of the rebinding rate π _si. The simulation results for three different values of the coupling parameter K, corresponding to the three transport regimes for kinesin as introduced in [25], are well described by the linear relation in (41), where we have used ε ₂ as a fit parameter, see inset in Fig. 9(a). These values of ε ₂ are in good agreement with the average values in Table 2. When the ratio $\mathcal{P}_{2}/\mathcal{P}_{1}$ is less than 1, the motor pair walk is dominated by the 1-motor runs whereas it is dominated by the 2-motor runs for $\mathcal{P}_{2}/\mathcal{P}_{1}>1$.

Fig. 9

(a) Ratio $\mathcal{P}_{2}/\mathcal{P}_{1}$ of the probability to be in a 2-motor run to the probability to be in a 1-motor run during a motor pair walk for three different coupling parameter: weak coupling K=0.02 pN/nm (red square), K=0.1 pN/nm (blue triangle) and strong coupling K=0.5 pN/nm (green circle) as a function of the rebinding rate π _si. Lines represent the results of the calculated ratio via (41) with ε ₂ in (39) for K=0 (dashed black line) and the fit parameter ε ₂ for K>0 (red, blue and green lines). The dotted line corresponds to $\mathcal{P}_{2}/\mathcal{P}_{1}=1$. (b) Crossover line $\mathcal{P}_{2}/\mathcal{P}_{1}=1$ as a function of the coupling parameter K and the characteristic rebinding rate π _c rescaled by the single motor overall unbinding rate ε _si=0.65/s. For $\mathcal{P}_{1}=\mathcal{P}_{2}$ (black line) 1-motor runs are as likely as 2-motor runs. 1-motor runs with $\mathcal{P}_{1} > \mathcal{P}_{2}$ are dominant for relatively small values of π _si/ε _si, whereas dominant 2-motor runs with $\mathcal{P}_{2}> \mathcal{P}_{1}$ require large values of π _si/ε _si

As shown in Fig. 9(a), the ratio $\mathcal {P}_{2}/\mathcal{P}_{1}$ depend linearly on the rebinding rate π _si. Inspection of Fig. 9(a) also reveals that the ratio $\mathcal{P}_{2}/\mathcal{P}_{1}$ is strongly reduced for increasing coupling parameter K, which implies that the termination rate ε ₂ of the 2-motor runs is strongly increased by interference effects arising from the motor-motor interactions. Observing dominant 2-motor runs of a strongly coupled motor pair requires a large rebinding rate with π _si≥4/s, whereas weakly coupled motor pairs have as many 2-motor runs as 1-motor runs for a relatively small rebinding rate π _si≃1.5/s. The expression in (41) implies that the characteristic rebinding rate π _c, at which $\mathcal {P}_{1}=\mathcal{P}_{2}$ for a given coupling parameter K, determines the 2-motor run termination rate ε ₂(K)=π _c.

The crossover line, at which $\mathcal{P}_{1}=\mathcal{P}_{2}$, is shown in Fig. 9(b) as a function of the coupling parameter and the rebinding rate. The characteristic rebinding rate π _c is rescaled by the single motor overall unbinding rate ε _si=0.65/s. This crossover line separates the parameter regime, in which 1-motor runs dominate the cargo run, from the regime, in which 2-motor runs are more likely. The motor pair spends most of its time in 1-motor runs for all coupling parameters if we choose a relatively small rebinding rate, whereas a dominance of 2-motor runs requires relatively large rebinding rates.

8 Motor Pair Parameters from Cargo Trajectories

As mentioned before, even though the chemomechanical network of a motor pair is rather complex, it involves only two new parameters, the single motor rebinding rate π _si and the coupling parameter K. In the simulations, we can choose certain values for these parameters. Such a choice is not possible in experimental studies, where those two parameters depend on molecular architecture of the cargo/motor complex. Therefore, we will now describe procedures, by which one can deduce the values of π _si and K from the observation and analysis of cargo trajectories. In fact, the properties of the 1-motor and 2-motor runs allow us to determine these two parameters separately: 1-motor run properties depend on the rebinding rate π _si but not on the coupling parameter K whereas 2-motor run properties depend on the coupling parameter K but not on the rebinding rate π _si.

Measuring the 1-motor run time 〈Δt ₁〉 in the cargo trajectories of the motor pair as in Fig. 8, the rebinding rate π _si can be calculated via relation (37) or

(49)

Further investigation of the cargo trajectories in Fig. 8 provide the average 2-motor run time 〈Δt ₂〉 of a cargo run, which determines the coupling parameter K. The 2-motor run time 〈Δt ₂〉, rescaled by the single motor run time, is shown in Fig. 10 as a function of the coupling parameter K. If the interactions between the two motors can be neglected, i.e., for K=0, one has 〈Δt ₂〉=〈t _si〉/2 as in (39). The 2-motor run time decreases with increasing coupling parameter in a roughly double exponential manner. There is a sharp decline to 30 % of the single motor run time at small coupling parameters K<0.1 pN/nm. For larger coupling parameters, the 2-motor run time decreases more slowly. In general, the relation between 〈Δt ₂〉 and K depends on the ATP concentration. For strong coupling, K=0.5 pN/nm, the 2-motor run time has dropped to 20 % of the single motor run time at small ATP-concentrations and to 15 % at saturating ATP-concentration. Therefore, a significant drop in the run time, compared to the single motor run time implies a strongly coupled motor pair. Measuring the 2-motor run time in cargo trajectories of the motor pair as in Fig. 8 gives access to the coupling parameter K of the motor pair and therefore the spring constant κ of the motor stalk.

Fig. 10

Average 2-motor run time 〈Δt ₂〉, in units of the single motor run time 〈t _si〉, as a function of the coupling parameter K for saturating [ATP] = 1 mM (black line) with 〈t _si〉=1.55 s, for [ATP] = 0.1 mM (red line) with 〈t _si〉=1.69 s, and for small [ATP] = 10 μM (blue line) with 〈t _si〉=1.84 s. If the interactions between the two motors can be neglected and K=0, one has 〈Δt ₂〉=〈t _si〉/2 as in (39)

9 Motor Pair Parameters from Individual Motor Trajectories

Alternatively, the motor pair parameters π _si and K can be determined by focusing not on the cargo trajectory, but on the individual motors of a motor pair and analyzing the probability distribution of the extension ΔL of the motor-motor separation. Here, the rebinding rate π _si can be determined in the same manner as before, since the 1-motor runs are easily detectable by one missing trace.

Labeling the individual motors of a motor pair, as has been done by [39] for individual heads of dynein motors, would allow to follow the individual motor trajectories during a cargo run. From these latter trajectories, we can deduce the distribution of the extension ΔL of the motor-motor separation. Since we defined ΔL≡0 for 1-motor runs, this is a property of the 2-motor runs. We will now show, that one can determine the coupling parameter K by measuring the width and the amplitude of the distribution for the extension ΔL of the motor-motor separation.

The individual motor trajectories of the leading and the trailing motor of a motor pair are shown in Fig. 11(a) for two different coupling parameters, weak coupling with K=0.02 pN/nm and strong coupling with K=0.5 pN/nm. In order to directly display the extension ΔL in the trajectories, the individual traces are plotted in the dimensionless form

(50)

i.e., in units of the stepsize ℓ, which implies $\bar {x}_{\mathrm{le}} -\bar{x}_{\mathrm{tr}}=\Delta L/\ell$, compare (21). Inspection of Fig. 11(a) shows that the motors of the weakly coupled motor pair separate up to ΔL=5ℓ, whereas those of the strongly coupled motor pair are at most two steps apart.

Fig. 11

(a) Individual motor trajectories of the leading (black line) and the trailing (red line) motor of a motor pair during a 2-motor run for two different coupling parameters, weak coupling with K=0.02 pN/nm and strong coupling with K=0.5 pN/nm. The individual runs are rescaled by the step size ℓ of a single motor and the position of the leading motor is displaced by L ₀, see (50). As a consequence, the separation $\bar{x}_{\mathrm{le}}-\bar{x}_{\mathrm{tr}}$ of the black and the red lines directly provides the spring extension ΔL in units of the stepsize ℓ. (b) Probability distribution $\mathcal{P}(\Delta L)$ of the extension ΔL of the motor-motor separation, in the units of the step size ℓ, during 2-motor runs for two different values of the coupling parameter K. For weak coupling with K=0.02 pN/nm (red line), the extensions are governed by a broad distribution whereas the distribution has a narrow peak at ΔL=0 for strong coupling with K=0.5 pN/nm (green line). The arrows indicate the width σ of the distributions. The nucleotide concentrations were set to [ATP] = 1 mM and [ADP] = [P] = 10 μM for both plots

The extension ΔL of the motor-motor separation during 2-motor runs represents a stochastic variable that is governed by a certain probability distribution $\mathcal{P}$ that can be determined by stochastic simulations. The probability distribution $\mathcal{P}(\Delta L)$ of the extension ΔL, in units of the stepsize ℓ, is shown in Fig. 11(b) for two different values of the coupling parameter K. For weak coupling, the extensions are governed by a broad distribution whereas this distribution has a narrow peak at ΔL=0 for strong coupling. The probability $\mathcal{P}(\Delta L)$ in Fig. 11(b) and Fig. 12(a) is symmetrically distributed around the average of 〈ΔL〉=0 for all coupling parameters, which implies that the leading and trailing motor are interchangeable with each other. The red line in Fig. 12(a) indicates the maximal values of the extension ΔL observed in the simulations. Inspection of this figure also shows that the number of accessible ΔL-values decrease for increasing coupling parameter K. Within the studied range 0.02≤K [pN/nm]≤0.5 for the coupling parameter, the number of accessible ΔL-values varies by one order of magnitude. Hence, a weakly coupled motor pair spends more time in motor pair states with |ΔL|≫1 than a strongly coupled motor pair. However, the interaction force (23) that the weakly coupled motor pair generates for |ΔL|≫1 is typically small compared to the interaction force generated within a single step of a strongly coupled motor pair. Indeed, for weak coupling with K=0.02 pN/nm and ΔL=10ℓ, for instance, the interaction force with F _le,tr=1.6 pN is still smaller than the interaction force F _le,tr=4 pN for strong coupling with K=0.5 pN/nm and ΔL=ℓ.

Fig. 12

(a) Contour plot (gray-scale map) of the probability distribution $\mathcal{P}(\Delta L)$ for the spring extension ΔL of the motor-motor separation as a function of the coupling parameter K. The extension ΔL is given in the units of the step size ℓ, the ATP concentration was chosen to be [ATP] = 1 mM. For weak coupling, extensions are governed by a broad distribution whereas the distribution has a narrow peak for strong coupling. The red line indicates maximal values of the extension ΔL observed in the simulations. The gray-scale map starts with small values of $\mathcal{P}(\Delta L)$ in white to large values of $\mathcal {P}(\Delta L)$ in black. (b) Width σ (black lines) and amplitude $\mathcal {P}(\Delta L=0)$ (red lines) of the distribution $\mathcal{P}(\Delta L)$ as a function of the coupling parameter K in a semilogarithmic plot for different ATP-concentrations: saturating [ATP] = 1 mM (solid lines), [ATP] = 0.1 mM (dashed lines) and small [ATP] = 10 μM (dotted lines)

The width σ and the peak amplitude $\mathcal {P}(\Delta L=0)$ of the probability distribution $\mathcal{P}(\Delta L)$ are shown in Fig. 12(b) as functions of the coupling parameter K for different ATP-concentrations. While the amplitude $\mathcal{P}(\Delta L=0)$ increases exponentially, the width σ decreases in an double exponential manner with increasing K. For noninteracting motors, with K=0, the width σ decreases from σ=7ℓ for saturating ATP-concentration to σ=3.5ℓ for small ATP-concentration while the amplitude increases from $\mathcal{P}(\Delta L=0)=0.08$ to $\mathcal{P}(\Delta L=0)=0.2$. For strong coupling, K=0.5 pN/nm, variations in the ATP-concentration hardly affect the distribution $\mathcal{P}(\Delta L)$. In this case width is σ=0.9ℓ for saturating ATP-concentration and σ=0.8ℓ for small ATP-concentration, respectively, and the amplitude increases from $\mathcal{P}(\Delta L=0)=0.38$ to $\mathcal{P}(\Delta L=0)=0.47$.

Thus, the analysis of individual motor trajectories of a motor pair provides the probability distribution $\mathcal{P}(\Delta L)$ for the extension ΔL of the motor-motor separation of a 2-motor run. Measuring the width σ and the peak amplitude $\mathcal {P}(\Delta L=0)$ of this probability distribution allows to determine the coupling parameter K of the motor pair and therefore the spring constant κ of the motor stalk.

10 Summary and Outlook

In this paper, we studied the dynamics of two elastically coupled kinesin motors. When a single motor is bound to the filament at a certain spatial position, it can attain different chemical states depending on the nucleotides bound to the two motor domains or heads. These different states are embodied in the chemomechanical network for a single motor as displayed in Fig. 1. The state of the elastically coupled motor pair is characterized by the chemical states of the two individual motors and, in addition, by the spatial separation of the two motors. This separation changes whenever one of the two motors performs a forward or backward step. Since the elastic coupling via the two motor stalks can be described by a single effective spring with coupling parameter K, see Sect. 3.1.1 and Fig. 4, the changes in the motor-motor separation can be described by the extension ΔL of this effective spring. In this way, each state of the motor pair is described by three variables, the chemical states i _le and i _tr of the leading and trailing motor as well as of the extension ΔL. The resulting chemomechanical network has a layer structure as shown in Fig. 5, where each layer corresponds to a constant value of ΔL. Even though the chemomechanical network of the motor pair as shown in Fig. 5 has a rather complex structure, this network involves, apart from the single motor parameters, only two additional parameters, namely the coupling parameter K of the motor pair assembly and the rebinding rate π _si of a single motor.

The elastic coupling as described by ΔL leads to mutual interaction forces between the two motors as in (22) and (23). Thus, each motor experiences an effective load force arising from the elastic interaction with the other motor. It is important to note that, in general, all chemical and mechanical transition rates of a single motor depend on the load force, see the generic form (2) of the transition rates. Thus, when one of the two motors performs a mechanical step, the motor-motor separation, the extension ΔL, and the elastic interaction forces are changed, which affects the chemical and mechanical transition rates of both motors. Because the resulting network consists of a huge number of cycles and the dependence of these single motor rates on force is highly nonlinear, see the relations (4) and (5), reflecting the complex molecular structure of the motor proteins, the network dynamics is not amenable to analytical methods. Therefore, we used the Gillespie algorithm in order to study this dynamics and to generate trajectories of the motor pair, where we distinguish cargo trajectories from the trajectories of the individual motors.

Inspection of cargo trajectories as in Fig. 6(a) and Fig. 8(a) reveals that a cargo transported by two motors is displaced by 4 nm when one of the motors performs an 8 nm step, in close analogy to the experimental results on gliding assays [33]. Furthermore, the stepping rate of a 2-motor run is almost twice the stepping rate of a 1-motor run. The latter corresponds to the completion time for the forward cycle of a single motor.

The relationship between decreasing cargo velocity and increasing coupling parameter K is reflected in the different slopes of the two trajectories depicted in Fig. 8(a). Thus, weakly coupled motor pairs spend more time in a 2-motor run compared to strongly coupled pairs. As expected, the run time distribution for the 1-motor runs is similar for both trajectories, see Fig. 8(b), since the properties of 1-motor runs should not depend on the elastic coupling. The average value 〈Δt ₁〉 of the 1-motor run times as deduced from the trajectories is in good agreement with the value obtained via expression (37), which can be understood from the simple 3-state network displayed in Fig. 7.

The latter network describes the three activity states of the motor pair. These three states represent 2- and 1-motor runs as well the unbound cargo. Which activity state is dominant depends on the single motor rebinding rate π _si and, via the 2-motor termination rate ε ₂, on the coupling parameter K. The corresponding activity regimes are shown in Fig. 13. The crossover line $\mathcal{P}_{2}=\mathcal{P}_{1}$ separates the parameter regime, in which 1-motor runs dominate the cargo runs, from the regime, in which 2-motor runs are more likely. If we choose a relatively small rebinding rate, the motor pair spends most of its time in 1-motor runs for all values of the coupling parameter, whereas a dominance of 2-motor runs requires relatively large rebinding rates. The crossover lines with $\mathcal{P}_{1}= 2\, \mathcal{P}_{2}$ and $\mathcal{P}_{2}=2\,\mathcal{P}_{1}$, indicated by the broken and dotted black lines in Fig. 13, provide more detailed information about the dominance of 1-motor and 2-motor runs. A small rebinding rate with π _si≤ε _si leads to a clear dominance of 1-motor runs with $\mathcal{P}_{1}\geq2 \mathcal{P}_{2}$ for all values of the coupling parameter. In contrast, a clear dominance of 2-motor runs with $\mathcal{P}_{2} \geq 2\mathcal{P}_{1}$ is only found for small values of the coupling parameter and relatively large rebinding rates π _si≥4ε _si.

Fig. 13

Activity regimes as a function of the coupling parameter K and the single motor rebinding rate π _si, where the latter rate is given in units of the overall unbinding rate ε _si=0.65/s for a single kinesin motor. The lines correspond to constant values of the ratio $\mathcal {P}_{2}/\mathcal{P}_{1}$ between the probabilities $\mathcal{P}_{2}$ and $\mathcal{P}_{1}$ that the cargo performs a 2- and 1-motor run, respectively. The full line represents $\mathcal {P}_{1}=\mathcal{P}_{2}$ as in Fig. 9(b). The dashed and the dotted black lines are the crossover lines, at which $\mathcal{P}_{1}=2 \mathcal{P}_{2}$ and $\mathcal{P}_{2}=2\mathcal{P}_{1}$, respectively. Thus, for each value of K, 2-motor runs dominate for large π _si whereas 1-motor runs dominate for small π _si

In the stochastic simulations, we studied the trajectories as generated from the chemomechanical network of the motor pair for certain values of the single motor rebinding rate π _si and the elastic coupling parameter K. In experimental studies, the values of these two parameters are not known but have to be determined in a consistent manner. Therefore, we show in Sects. 8 and 9 how one can deduce the values of these two parameters from the statistical properties of the trajectories. The single motor rebinding rate π _si can be directly obtained, via relation (49), from the average 1-motor run time 〈Δt ₁〉 and the single motor unbinding rate ε _si as defined in (8). The coupling parameter K, on the other hand, can be deduced in two different ways. First, one can determine K by measuring the average value 〈Δt ₂〉 of the 2-motor run time and using the functional relationship between K and 〈Δt ₂〉 as displayed in Fig. 10. As shown in this figure, this relationship depends on the ATP concentration but this dependence is not very pronounced. Second, the coupling parameter K can be determined from the trajectories of the individual motors by analyzing the probability distribution for the extension ΔL of the motor-motor separation of a 2-motor run, see Fig. 12(a). Both the width σ and the peak amplitude $\mathcal{P}(\Delta L=0)$ of this probability distribution can be used to deduce the coupling parameter K by using the functional relationship displayed in Fig. 12(b). This relationship again exhibits a relatively weak dependence on the ATP concentration.

In our previous theoretical studies on cooperative cargo transport by identical motors [24, 25], the chemical and mechanical transitions of the single motors, which determine the free energy transduction of these motors, were not taken into account explicitly but only in a coarse-grained manner via the resulting force-velocity relationships. For transport by two motors and small values of the elastic coupling parameter K corresponding to noninteracting motors, our results are consistent with those in Ref. [24]. For larger values of the K, mutual interaction forces are no longer negligible and will lead to a variety of interference effects as recently discussed in Ref. [25]. In agreement with the latter results, we find in Fig. 10 that the 2-motor run time is significantly decreased for strongly coupled compared to weakly coupled motor pairs. In addition, we are able to predict the dependence of the transport properties on the nucleotide concentrations, as shown in Fig. 10 and Fig. 12(b) which exhibit results for different ATP concentrations.

In the present study, we focused on the behavior of two elastically coupled motors in the absence of an external load force. It is straightforward to incorporate such a force both into the force balance relations and into the chemomechanical network for the motor pair. We will describe the resulting force-dependent behavior in a forthcoming paper. It is then also possible to perform a detailed comparison with the experimental observations on the force-dependent cargo velocity and run length.