Open Shop Scheduling with Synchronization

Abstract

In this paper, we study open shop scheduling problems with synchronization. This model has the same features as the classical open shop model, where each of the n jobs has to be processed by each of the m machines in an arbitrary order. Unlike the classical model, jobs are processed in synchronous cycles, which means that the m operations of the same cycle start at the same time. Within one cycle, machines which process operations with smaller processing times have to wait until the longest operation of the cycle is finished before the next cycle can start. Thus, the length of a cycle is equal to the maximum processing time of its operations. In this paper, we continue the line of research started by Weiß et al. (Discrete Appl Math 211:183–203, 2016). We establish new structural results for the two-machine problem with the makespan objective and use them to formulate an easier solution algorithm. Other versions of the problem, with the total completion time objective and those which involve due dates or deadlines, turn out to be NP-hard in the strong sense, even for $m=2$ machines. We also show that relaxed models, in which cycles are allowed to contain less than m jobs, have the same complexity status.

1 Introduction

Scheduling problems with synchronization arise in applications where job processing includes several stages, performed by different processing machines, and all movements of jobs between machines have to be done simultaneously. This may be caused by special requirements of job transfers, as it happens, for example, if jobs are installed on a circular production unit which rotates to move jobs simultaneously to machines of the next stage (see Soylu et al. 2007; Huang 2008; Waldherr and Knust 2014). Alternatively, there may be health and safety regulations requiring that no machine is in operation while jobs are being removed from or moved to a machine. Similar synchronization takes place in the context of switch-based communication systems, where senders transmit messages to receivers in a synchronous manner, as this eliminates possible clashes for receivers (see Gopal and Wong 1985; Rendl 1985; Kesselman and Kogan 2007).

Synchronization arises naturally in assembly line systems where each assembly operation may start only after all preceding operations are completed, see Doerr et al. (2000), Chiang et al. (2012), and Urban and Chiang (2016), and the survey by Boysen et al. (2008). In the context of shop scheduling models, synchronization aspects were initially studied for flow shops (Soylu et al. 2007; Huang 2008; Waldherr and Knust 2015), and later for open shops (Weiß et al. 2016). In the latter paper the makespan problem is addressed, with the main focus on the underlying assignment model. In the current paper we continue that line of research, elaborating further the study of the makespan minimization problem and addressing other variants of the model with different objective functions.

Formally, the open shop model with synchronization is defined as follows. As in the classical open shop, n jobs $J_{1},J_{2},\ldots ,J_{n}$ have to be processed by m machines $M_{1},M_{2},\ldots ,M_{m}, n\ge m$. Each job $J_{j}, 1\le j\le n$, consists of m operations $O_{ij}$ for $1\le i\le m$, where $O_{ij}$ has to be processed on machine $M_{i}$ without preemption for $p_{ij}$ time units. The synchronization requirement implies that job processing is organized in synchronous cycles, with operations of the same cycle starting at the same time. Within one cycle, machines which process operations of smaller processing times have to wait until the longest operation of the cycle is finished before the next cycle can start. Thus, the length of a cycle is equal to the maximum processing time of its operations. Similar to the classical open shop model, we assume that unlimited buffer exists between the machines, i.e., jobs which are finished on one machine can wait for an arbitrary number of cycles to be scheduled on the next machine.

The goal is to assign the nm operations to the m machines in n cycles such that a given objective function f is optimized. Function f depends on the completion times $C_{j}$ of the jobs $J_{j}$, where $C_{j}$ is the completion time of the last cycle in which an operation of job $J_{j}$ is scheduled. Following the earlier research by Huang (2008) and Waldherr and Knust (2015), we denote synchronous movement of the jobs by “synmv” in the $\beta$-field of the traditional three-field notation. We write O|synmv|f for the general synchronous open shop problem with objective function f and Om|synmv|f if the number m of machines is fixed (i.e., not part of the input). The most common objective function is to minimize the makespan $C_{\max }$, defined as the completion time of the last cycle of a schedule. If deadlines $D_{j}$ are given for the jobs $J_{j}$, the task is to find a feasible schedule with all jobs meeting their deadlines, $C_{j}\le D_{j}$ for $1\le j\le n$. We use the notation $O|synmv,C_{j}\le D_{j}|-$ for the feasibility problem with deadlines. In problem $O|synmv|\sum C_{j}$ the sum of all completion times has to be minimized.

Usually, we assume that every cycle contains exactly m operations, one on each machine. In that case, together with the previously stated assumption $n\ge m$, exactly n cycles are needed to process all jobs. However, sometimes it is beneficial to relax the requirement for exactly m operations per cycle. Then a feasible schedule may contain incomplete cycles, with less than m operations. We denote such a relaxed model by including “rel” in the $\beta$-field. Similar to the observation of Kouvelis and Karabati (1999) that introducing idle times in a synchronous flow shop may be beneficial, we will show that a schedule for the relaxed problem O|synmv, rel|f consisting of more than n cycles may outperform a schedule for the nonrelaxed problem O|synmv|f with n cycles.

The synchronous open shop model is closely related to long known optimization problems in the area of communication networks: the underlying model is the max-weight edge coloring problem (MEC), restricted to complete bipartite graphs, see Weiß et al. (2016) for the link between the models, and Mestre and Raman (2013) for the most recent survey on MEC and other versions of max-coloring problems. As stated in Weiß et al. (2016), the complexity results from Rendl (1985) and Demange et al. (2002), formulated for MEC, imply that problems $O|synmv|C_{\max }$ and $O|synmv,rel|C_{\max }$ are strongly NP-hard if both n and m are part of the input. Moreover, using the results from Demange et al. (2002), Escoffier et al. (2006), Kesselman and Kogan (2007), de Werra et al. (2009), and Mestre and Raman (2013), formulated for MEC on cubic bipartite graphs, we conclude that these two open shop problems remain strongly NP-hard even if each job is processed by at most three machines and if there are only three different values for nonzero processing times.

On the other hand, if the number of machines m is fixed, then problem $Om|synmv|C_{\max }$ can be solved in polynomial time as m-dimensional assignment problem with a nearly Monge weight array of size $n\times \cdots \times n$, as discussed in Weiß et al. (2016) and in Sect. 2 of the current paper. The relaxed version $Om|synmv,rel|C_{\max }$ admits the same assignment model, but with a larger m-dimensional weight array extended by adding dummy jobs. As observed in Weiß et al. (2016), the number of dummy jobs can be bounded by $(m-1)n$. Both problems, $Om|synmv|C_{\max }$ and $Om|synmv,rel|C_{\max }$, are solvable in ${{\mathcal {O}}}(n)$ time, after operations are sorted in nonincreasing (or nondecreasing) order of processing times on all machines. However, this algorithm becomes impractical for larger instances, as the constant term of the linear growth rate exceeds $(m!)^{m}$.

The remainder of this paper is organized as follows. In Sect. 2, we consider problem $O2|synmv|C_{\max }$ and establish a new structural property of an optimal solution. Based on it we formulate a new (much easier) ${{\mathcal {O}}}(n)$-time solution algorithm, assuming jobs are presorted on each machine. Then we address in more detail problem $O|synmv,rel|C_{\max }$ and provide a tight bound on the maximum number of cycles needed to get an optimal solution. In Sects. 3 and 4 we show that problems $O2|synmv, C_j \le D_j|-$ and $O2|synmv|\sum C_j$ are strongly NP-hard. Finally, conclusions are presented in Sect. 5.

2 Minimizing the makespan

In this section, we consider synchronous open shop problems with the makespan objective. Recall that problem $Om|synmv|C_{\max }$ with a fixed number of machines m can be solved in ${{\mathcal {O}}}(n)$ time (after presorting) by the algorithm from Weiß et al. (2016). In Sect. 2.1 we elaborate further results for the two-machine problem $O2|synmv|C_{\max }$, providing a new structural property of an optimal schedule, which results in an easier solution algorithm. In Sect. 2.2 we study the relaxed problem $O|synmv,rel|C_{\max }$ and determine a tight bound on the maximum number of cycles in an optimal solution.

2.1 Problem $O2|synmv|C_{\max }$

Problem $O2|synmv|C_{\max }$ can be naturally modeled as an assignment problem. Consider two nonincreasing sequences of processing times of the operations on machines $M_{1}$ and $M_{2}$, renumbering the jobs in accordance with the sequence on $M_{1}$:

$$\begin{aligned} p_{11}\ge p_{12}\ge \ldots \ge p_{1n},\ p_{2k_{1}}\ge p_{2k_{2}}\ge \ldots \ge p_{2k_{n}}. \end{aligned}$$

To simplify the notation, let $(a_{i})_{i=1}^{n}$ and $(b_{j})_{j=1}^{n}$ be the corresponding sequences of processing times in nonincreasing order. The ith operation on $M_{1}$ with processing time $a_{i}$ and the jth operation on $M_{2}$ with processing time $b_{j}$ can be paired in a cycle with cycle time $\max \{a_{i},b_{j}\}$ if these two operations are not associated with the same job. Let ${{\mathcal {F}}}=\{(1,j_{1}),(2,j_{2}),\ldots ,(n,j_{n})\}$ be the set of forbidden pairs: $(i,j_{i})\in {{\mathcal {F}}}$ if operations $O_{1i}$ and $O_{2j_{i}}$ belong to the same job.

Using binary variables $x_{ij}$ to indicate whether the ith operation on $M_1$ and the jth operation on $M_2$ (in the above ordering) are paired in a cycle, the problem can be formulated as the following variant of the assignment problem:

$$\begin{aligned} \begin{array}{llll} {{\mathrm {AP}}}_{{{\mathcal {F}}}}{{\mathrm {:}}} &{} \min &{} \sum \limits _{i=1}^{n} \sum \limits _{j=1}^{n}w_{ij}x_{ij} &{} \\ &{} {{\mathrm {s.t.}}} &{} \sum \limits _{i=1}^{n}x_{ij}=1, &{} 1\le j\le n, \\ &{} &{} \sum \limits _{j=1}^{n}x_{ij}=1, &{} 1\le i\le n, \\ &{} &{} x_{ij}\in \{0,1\}, &{} 1\le i,j\le n, \\ &{} &{} x_{ij}=0, &{} (i,j)\in {{\mathcal {F}}}, \end{array} \end{aligned}$$

with the cost matrix ${{\mathcal {W}}}=(w_{ij})$, where

$$\begin{aligned} \begin{array}{ll} w_{ij}=\max \left\{ a_{i},b_{j}\right\} ,&1\le i,j\le n. \end{array} \end{aligned}$$

(1)

Due to the predefined 0-variables $x_{ij}=0$ for forbidden pairs of indices $(i,j)\in {{\mathcal {F}}}$ it is prohibited that two operations of the same job are allocated to the same cycle.

In Weiß et al. (2016) a slightly different formulation is used to model synchronous open shop as an assignment problem:

$$\begin{aligned} \begin{array}{llll} {{\mathrm {AP}}}_{\infty }{{\mathrm {:}}} &{} \min &{} \sum \limits _{i=1}^{n} \sum \limits _{j=1}^{n}c_{ij}x_{ij} &{} \\ &{} {{\mathrm {s.t.}}} &{} \sum \limits _{i=1}^{n}x_{ij}=1, &{} 1\le j\le n, \\ &{} &{} \sum \limits _{j=1}^{n}x_{ij}=1, &{} 1\le i\le n, \\ &{} &{} x_{ij}\in \{0,1\}, &{} 1\le i,j\le n, \end{array} \end{aligned}$$

with the cost matrix ${{\mathcal {C}}}=(c_{ij})$, where for $1\le i,j\le n$

$$\begin{aligned} c_{ij}=\left\{ \begin{array}{ll} \max \left\{ a_{i},b_{j}\right\} , &{} \hbox { if } (i,j)\notin {{\mathcal {F}}}, \\ \infty , &{} \hbox { if } (i,j)\in {{\mathcal {F}}}. \end{array} \right. \end{aligned}$$

(2)

Here, for the forbidden pairs $(i,j) \in {{\mathcal {F}}}$ there are $\infty$-entries in the cost matrix, one in every row and every column. A feasible solution of the open shop problem exists if and only if the optimal solution value of ${{\mathrm {AP}}}_{\infty }$ is less than $\infty$.

Note that the problem ${{\mathrm {AP}}}_{\infty }$ in its more general form is the subject of our related paper, Weiß et al. (2016). In the current paper we focus on the formulation ${{\mathrm {AP}}}_{{\mathcal {F}}}$, which is equivalent to ${{\mathrm {AP}}}_{\infty }$ for costs $c_{ij}$ of form (2). Formulation ${{\mathrm {AP}}}_{{\mathcal {F}}}$ allows us to produce stronger results, see Theorems 1–2 in the next section. The main advantage of formulation ${{\mathrm {AP}}}_{{{\mathcal {F}}}}$ is the possibility to use finite w-values for all pairs of indices, including $w_{ij}$’s defined for forbidden pairs $(i,j) \in {{\mathcal {F}}}$.

Example 1

Consider an example with $n=4$ jobs and the following processing times:

$$\begin{aligned}\begin{array}{c|cccc} j &{} 1 &{} 2 &{} 3 &{} 4 \\ \hline p_{1j} &{} ~7~ &{} ~5~ &{} ~3~ &{} ~2~ \\ p_{2j} &{} 3 &{} 4 &{} 6 &{} 2 \end{array} \end{aligned}$$

The sequences $(a_{i})$ and $(b_{j})$ of processing times are of the form:

$$\begin{aligned}\begin{array}{c|cccc} i &{} 1 &{} 2 &{} 3 &{} 4 \\ \hline a_{i} &{} 7 &{} 5 &{} 3 &{} 2 \\ {{\mathrm {Job}}} &{} J_{1} &{} J_{2} &{} J_{3} &{} J_{4} \end{array} \qquad \begin{array}{c|cccc} j &{} 1 &{} 2 &{} 3 &{} 4 \\ \hline b_{j} &{} 6 &{} 4 &{} 3 &{} 2 \\ {{\mathrm {Job}}} &{} J_{3} &{} J_{2} &{} J_{1} &{} J_{4} \end{array} \end{aligned}$$

The forbidden pairs are ${{\mathcal {F}}}=\{(1,3),(2,2),(3,1),(4,4)\}$, the associated matrices ${{\mathcal {W}}}$ and ${{\mathcal {C}}}$ are

$$\begin{aligned} {{\mathcal {W}}}=\left( \begin{array}{c|cccc} i\setminus j &{} ~1~ &{} ~2~ &{} ~3~ &{} ~4~ \\ \hline 1 &{} 7 &{} {{\mathbf {7}}} &{} 7 &{} 7 \\ 2 &{} \mathbf {6} &{} 5 &{} 5 &{} 5 \\ 3 &{} 6 &{} 4 &{} 3 &{} \mathbf {3} \\ 4 &{} 6 &{} 4 &{} \mathbf {3} &{} 2 \end{array}\right) , ~~ \mathcal {C}=\left( \begin{array}{c|cccc} i\setminus j &{} 1 &{} 2 &{} 3 &{} 4 \\ \hline 1 &{} 7 &{} \mathbf {7} &{} \infty &{} 7 \\ 2 &{} \mathbf {6} &{} \infty &{} 5 &{} 5 \\ 3 &{} \infty &{} 4 &{} 3 &{} \mathbf {3} \\ 4 &{} 6 &{} 4 &{} \mathbf {3} &{} \infty \end{array} \right) . \end{aligned}$$

Fig. 1

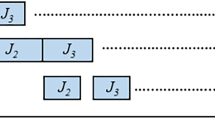
Gantt chart of an optimal schedule for Example 1

The entries in bold font in ${{\mathcal {W}}}$ and $\mathcal {C}$ correspond to the optimal solution illustrated in Fig. 1. Here, $x_{12}=1$ for the pair of jobs $J_{1},J_{2}$ assigned to the same cycle, and $x_{23}=x_{34}=x_{41}=1$ for the other cycles. The makespan is $7+6+3+3=19$.

It is known (cf. Bein et al. 1995; Burkard et al. 1996) that matrix ${{\mathcal {W}}}=(w_{ij})$ defined by (1) satisfies the Monge property, i.e., for all row indices $1\le i<r\le n$ and all column indices $1\le j<s\le n$ we have

$$\begin{aligned} w_{ij}+w_{rs}\le w_{is}+w_{rj}. \end{aligned}$$

(3)

Without the additional condition on forbidden pairs ${{\mathcal {F}}}$, a greedy algorithm finds an optimal solution $\mathbf {X}=\left( x_{ij}\right)$ to the assignment problem and that solution is of the diagonal form:

$$\begin{aligned} x_{ii} =1 \text{ for } i=1,\ldots ,n; \quad x_{ij} =0 \text{ for } i\ne j. \end{aligned}$$

(4)

Forbidden pairs or, equivalently, $\infty$-entries, may keep the Monge property satisfied so that the greedy algorithm remains applicable, as discussed by Burkard et al. (1996) and Queyranne et al. (1998). However, if at least one of the forbidden pairs from ${{\mathcal {F}}}$ is a diagonal element, then solution (4) is infeasible for problem $\mathrm {AP}_{{{\mathcal {F}}}}$. A similar observation holds for problem $\mathrm { AP}_{\infty }$ if an $\infty$-entry lies on the diagonal. In that case, as demonstrated in Weiß et al. (2016), there exists an optimal solution $\mathbf {X}$ which satisfies a so-called corridor property: the 1-entries of $\mathbf {X}$ belong to a corridor around the main diagonal of width 2, so that for every $x_{ij}=1$ of an optimal solution the condition $|i-j|\le 2$ holds. Notice that in Example 1 there are two forbidden pairs in ${{\mathcal {F}}}$ of the diagonal type, (2, 2) and (4, 4); the specified optimal solution satisfies the corridor property. A related term used typically in two-dimensional settings is the bandwidth (see, e.g., Ćustić et al. 2014).

The corridor property is proved in Weiß et al. (2016) in its generalized form for the case of the m-dimensional assignment problem with a nearly Monge array (this is an array where $\infty$-entries are allowed and the Monge property has to be satisfied by all finite entries). Thus, this property also holds for the m-machine synchronous open shop problem. It appears that for the case of $m=2$ the structure of an optimal solution can be characterized in a more precise way, which makes it possible to develop an easier solution algorithm.

In the following, we present an alternative characterization of optimal solutions for $m=2$ and develop an efficient algorithm for constructing an optimal solution. Note that the arguments in Weiß et al. (2016) are presented with respect to problem $\mathrm {AP} _{\infty }$; in this paper our arguments are based on the formulation $\mathrm {AP }_{{{\mathcal {F}}}}$ and on its relaxation $\mathrm {AP}_{\mathcal {F=}\emptyset }$ , with the condition “$x_{ij}=0\$for $(i,j)\in {{\mathcal {F}}}$ ” dropped.

A block $\mathbf {X}_{h}$ of size s is a square submatrix consisting of $s\times s$ elements with exactly one 1-entry in each row and each column of $\mathbf {X}_{h}$. We call a block large if it is of size $s \ge 4$, and small otherwise. Our main result is establishing a block-diagonal structure of an optimal solution $\mathbf {X}=(x_{ij})$,

$$\begin{aligned} \mathbf {X}=\left( \begin{array}{ccccc} \mathbf {X}_{1} &{} \mathbf {0} &{} \mathbf {0} &{} \ldots &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {X}_{2} &{} \mathbf {0} &{} \ldots &{} \mathbf {0} \\ &{} &{} \ddots &{} &{} \\ \mathbf {0} &{} \ldots &{} \mathbf {0} &{} \mathbf {X}_{z-1} &{} \mathbf {0} \\ \mathbf {0} &{} \ldots &{} \mathbf {0} &{} \mathbf {0} &{} \mathbf {X}_{z} \end{array} \right) \end{aligned}$$

(5)

with blocks $\mathbf {X}_{h}, 1\le h\le z$, of the form

$$\begin{aligned} \left( \begin{array}{c} 1 \end{array} \right) , \qquad \left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \end{array} \right) , \qquad \left( \begin{array}{ccc} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \end{array} \right) , \qquad \left( \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 \end{array} \right) \end{aligned}$$

(6)

around the main diagonal, and 0-entries elsewhere. Note that the submatrix

$$\begin{aligned} \left( \begin{array}{ccc} 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \end{array} \right) \end{aligned}$$

is excluded from consideration.

Theorem 1

(“Small Block Property”): There exists an optimal solution to problem $\mathrm {AP}_{\mathbf {\mathcal {F}}}$ in block-diagonal structure, containing only blocks of type (6).

This theorem is proved in Appendix 1. The small block property leads to an efficient ${{\mathcal {O}}}(n)$-time dynamic programing algorithm to find an optimal solution. Here we use formulation $\mathrm {AP}_{\infty }$ rather than $\mathrm {AP}_{{{\mathcal {F}}}}$, as infinite costs can be easily handled by recursive formulae. The algorithm enumerates optimal partial solutions, extending them repeatedly by adding blocks of size 1, 2, or 3.

Let $S_{i}$ denote an optimal partial solution for a subproblem of $\mathrm { AP}_{\infty }$ defined by the submatrix of ${{\mathcal {W}}}$ with the first i rows and i columns. If an optimal partial solution $S_{i}$ is known, together with solutions $S_{i-1}$ and $S_{i-2}$ for smaller subproblems, then by Theorem 1 the next optimal partial solution $S_{i+1}$ can be found by selecting one of the following three options:

• extending $S_{i}$ by adding a block of size 1 with $x_{i+1,i+1}=1$; the cost of the assignment increases by $w_{i+1,i+1}$;

• extending $S_{i-1}$ by adding a block of size 2 with $x_{i,i+1}=x_{i+1,i}=1$; the cost of the assignment increases by $w_{i,i+1}+w_{i+1,i}$;

• extending $S_{i-2}$ by adding a block of size 3 with the smallest cost:

  • (i) $x_{i-1,i+1}=x_{i,i-1}=x_{i+1,i}=1$ with the cost $w_{i-1,i+1}+w_{i,i-1}+w_{i+1,i}$, or

  • (ii) $x_{i-1,i}=x_{i,i+1}=x_{i+1,i-1}$ with the cost $w_{i-1,i}+w_{i,i+1}+w_{i+1,i-1}$.

  Let $w(S_{i})$ denote the cost of $S_{i}$. Then

(7)

The initial conditions are defined as follows:

$$\begin{aligned} \begin{array}{l} w(S_{0})=0, \\ w(S_{1})=w_{11}, \\ w(S_{2})=\min \left\{ w_{11}+w_{22},~w_{12}+w_{21}\right\} . \end{array} \end{aligned}$$

Thus, $w(S_{3})$, ..., $w(S_{n})$ are computed by (7) in ${{\mathcal {O}}}(n)$ time.

Theorem 2

Problem $O2|synmv|C_{\max }$ can be solved in ${{\mathcal {O}}}(n)$ time.

Concluding this subsection, we provide several observations about the presented results. First, the small block property for problem $O2|synmv|C_{\max }$ has implications for the assignment problem $AP_{\infty }$ with costs (2) and for more general cost matrices. The proof of the small block property is presented for problem $AP_{{{\mathcal {F}}}}$. It is easy to verify that the proof is valid for an arbitrary Monge matrix ${{\mathcal {W}}}$, not necessarily of type (1); the important property used in the proof requires that the set ${{\mathcal {F}}}$ has no more than one forbidden pair $\left( i,j\right)$ in every row and in every column, and that all entries of the matrix ${{\mathcal {W}}}$, including those corresponding to the forbidden pairs ${{\mathcal {F}}}$, satisfy the Monge property. Thus, the small block property and the ${{\mathcal {O}}}(n)$-time algorithm hold for problem $AP_{\infty }$ if

• (i) there is no more than one $\infty$-entry in every row and every column of the cost matrix $\mathcal {C}$, and

• (ii) matrix $\mathcal {C}$ can be transformed into a Monge matrix by modifying only the $\infty$-entries, keeping other entries unchanged.

Note that not every nearly Monge matrix satisfying (i) can be completed into a Monge matrix satisfying (ii); see Weiß et al. (2016) for further details. However, the definition (2) of the cost matrix $\mathcal {C}$ for the synchronous open shop allows a straightforward completion by replacing every entry $c_{ij}=\infty$ by $c_{ij}=\max \left\{ a_{i},b_{j}\right\}$. While completability was not used in the proof of the more general corridor property presented in Weiß et al. (2016), the proof of the small block property depends heavily on the fact that the matrix of the synchronous open shop problem can be completed into a Monge matrix. In particular, we use completability when we accept potentially infeasible blocks in the proof of Lemma 3 and repair them later on with the help of Lemmas 4 and 5. In the literature, the possibility of completing an incomplete Monge matrix (a matrix with unspecified entries) was explored by Deineko et al. (1996) for the traveling salesman problem. They discuss Supnick matrices, a subclass of incomplete Monge matrices, for which completability is linked with several nice structural and algorithmic properties.

Finally, we observe that while the assignment matrices arising from the multimachine case are completable in the same way as for the two-machine case (see Weiß et al. 2016), it remains open whether this can be used to obtain an improved result for more than two machines as well. The technical difficulties of that case are beyond the scope of this paper.

2.2 Problem $O|synmv,rel|C_{\max }$

In this section, we consider the relaxed problem $O|synmv,rel|C_{\max }$ where more than n cycles are allowed, with unallocated (idle) machines in some cycles. This problem can be transformed to a variant of problem $O|synmv|C_{\max }$ by introducing dummy jobs, used to model idle intervals on the machines. Dummy jobs have zero-length operations on all machines, and it is allowed to assign several operations of a dummy job to the same cycle. Thus, in a feasible schedule with dummy jobs, all cycles are complete, but some of the m operations in a cycle may belong to dummy jobs.

Similar to the observation of Kouvelis and Karabati (1999) that introducing idle times in a synchronous flow shop may be beneficial, we show that a schedule for the relaxed open shop problem $O|synmv,rel|C_{\max }$ consisting of more than n cycles may outperform a schedule for the nonrelaxed problem $O|synmv|C_{\max }$ with n cycles.

Example 2

Consider an example with $m=3$ machines, $n=5$ jobs and the following processing times:

$$\begin{aligned} \begin{array}{l|ccccc} ~j &{} ~1~ &{} ~2~ &{} ~3~ &{} ~4~ &{} ~5~ \\ \hline p_{1j}~ &{} 3 &{} 2 &{} 4 &{} 3 &{} 1 \\ p_{2j} &{} 5 &{} 3 &{} 2 &{} 3 &{} 1 \\ p_{3j} &{} 4 &{} 5 &{} 1 &{} 4 &{} 1 \end{array} \end{aligned}$$

In the upper part of Fig. 2 an optimal schedule for problem $O3|synmv|C_{\max }$ with $n=5$ cycles and a makespan of 18 is shown. For the relaxed problem $O3|synmv,rel|C_{\max }$ adding a single dummy job $J_{6}$ leads to an improved schedule with 6 cycles and makespan 17 (see the lower part of Fig. 2).

The maximum total number of cycles of nonzero length is nm, which occurs if each of the nm “actual” operations is scheduled in an individual cycle. Then, in each of these nm cycles one actual operation and $m-1$ dummy operations are processed. To achieve a best schedule it is therefore sufficient to include $n(m-1)$ dummy jobs, each dummy job consisting of m zero-length operations. This implies that problem $Om|synmv,rel|C_{\max }$ for a fixed number m of machines can be solved in polynomial time by the algorithm from Weiß et al. (2016).

Fig. 2

An optimal schedule for $O3|synmv|C_{\max }$ and an improved schedule for $O3|synmv,rel|C_{\max }$ (with dummy job $J_{6}$)

For the two-machine case described in Sect. 2.1, if the actual jobs are numbered as $1,\ldots ,n$, and the dummy jobs are numbered as $n+1,\ldots ,2n$, then we apply the algorithm to the extended cost matrix $\mathcal {W~}^{\prime }$ obtained from the $n\times n$ matrix ${{\mathcal {W}}}$ defined by (2), by adding rows and columns $n+1,\ldots ,nm$ with entries

$$\begin{aligned} w_{ij}=\left\{ \begin{array}{lll} a_{i}, &{} i=1,\ldots ,n, &{} j=n+1,\ldots ,2n, \\ b_{j}, &{} i=n+1,\ldots ,2n, &{} j=1,\ldots ,n, \\ 0, &{} i=n+1,\ldots ,2n, &{} j=n+1,\ldots ,2n. \end{array} \right. \end{aligned}$$

Here combining an operation of an actual job (having processing time $a_{i}$ or $b_{j}$) with a dummy job incurs a cycle of length $a_{i}$ or $b_{j}$, while combining two dummy operations incurs an artificial cycle of 0 length, even if both operations belong to the same dummy job. For the case of multiple machines the cost matrix can be adjusted analogously, see Weiß et al. (2016) for details.

Clearly, for algorithmic purposes it is desirable to have the number of added dummy jobs as small as possible. As discussed in Waldherr et al. (2015), for the synchronous flow shop problem $F|synmv, rel|C_{\max }$, instances exist where for an optimal solution $(n-1)(m-2)$ dummy jobs are needed. In the following we show that for the open shop problem $O|synmv, rel|C_{\max }$ at most $m-1$ dummy jobs are needed to obtain an optimal solution.

Theorem 3

There exists an optimal solution to problem $O|synmv,rel|C_{\max }$ with at most $m-1$ dummy jobs, so that the number of cycles is at most $n+m-1$.

Proof

Let S be an optimal schedule with $\xi$ dummy jobs, $\xi \ge m$. We construct another schedule $\widetilde{S}$ with $C_{\max }(\widetilde{S} )\le C_{\max }(S)$ and $\xi -1$ dummy jobs. Notice that it is allowed to assign several operations of the same dummy job to any cycle.

Case 1 If there exists a cycle $I^{\prime }$ which consists solely of dummy operations of the same job $J_{d}\in \{J_{n+1},J_{n+2},\ldots ,J_{n+\xi }\}$, then that dummy job can be eliminated and $\widetilde{S}$ is found.

Case 2 If there exists a cycle $I^{\prime }$ which consists solely of dummy operations, some of which belong to different dummy jobs, then we can achieve Case 1 by selecting a dummy job $J_{d}$ arbitrarily and swapping its operations from outside $I^{\prime }$ with the dummy operations in $I^{\prime }$. The resulting schedule is feasible and has the same makespan.

Case 3 Suppose no cycle in S consists purely of dummy operations. Let $I^{\prime }$ be the shortest cycle and let $\nu$ be the number of actual operations in $I^{\prime }, 1\le \nu \le m$. We demonstrate that each actual operation processed in $I^{\prime }$ can be swapped with a dummy operation from another cycle.

Consider an actual operation $O_{ij}$ in cycle $I^{\prime }$ with machine $M_{i}$ processing job $J_{j}$. Select another cycle $I^{\prime \prime }$ (its existence is demonstrated below) such that it does not involve an operation of $J_{j}$ and has a dummy operation on $M_{i}$. Swap operations on $M_{i}$ in $I^{\prime }$ and $I^{\prime \prime }$, reducing the number of actual operations in $I^{\prime }$ by 1. Clearly, after the swap both cycles are feasible, because introducing a dummy operation into $I^{\prime }$ cannot cause a conflict, and because no operation of $J_j$ was processed in $I^{\prime \prime }$ before the swap. After the swap, both cycles $I^{\prime }$ and $I^{\prime \prime }$ have either the same length as before or cycle $I^{\prime }$ becomes shorter. Performing the described swaps for each actual operation $O_{ij}$ in cycle $I^{\prime }$, we arrive at Case 1 or 2.

A cycle $I^{\prime \prime }$ exists since

• there are at least $\xi$ cycles with a dummy operation on $M_{i}(\xi \ge m)$ and those cycles are different from $I^{\prime }$;

• there are exactly $m-1$ cycles with $J_{j}$ processed on a machine that differs from $M_{i}$, and those cycles are different from $I^{\prime }$. $\square$

We continue by demonstrating that the bound $m-1$ is tight.

Example 3

Consider an instance of problem $O|synmv,rel|C_{\max }$ with m machines, $n=m+1$ jobs and processing times $p_{ij}=2m$ for $i=1,\ldots ,m, j=1,\ldots ,n-1,$ and $p_{in}=1$ for $i=1,\ldots ,m$.

An optimal schedule consists of m complete cycles of length 2m each, containing operations of the jobs $\left\{ J_{1},J_{2},\ldots ,J_{m}\right\}$ only, and m incomplete cycles with the single actual job $J_{m+1}$ grouped with $m-1$ dummy jobs, see Fig. 3. The optimal makespan is $C_{\max }^{\mathrm {opt}}=2m^{2}+m$. In any schedule with less than $m-1$ dummy jobs, at least one operation of job $J_{m+1}$ is grouped with another operation of an actual job, the length of such a cycle being 2m. Thus, a schedule with less that $m-1$ dummy jobs consists of at least $m+1$ cycles of length 2m, so that the makespan is at least $2m(m+1)>C_{\max }^{\mathrm {opt}}$.

Notice that since our paper focuses on scheduling aspects, we have presented Theorem 3 in the scheduling language for the sake of consistency and self-containment. Knowing that $O|synmv,rel|C_{\max }$ is equivalent to the max-weight edge coloring problem on the complete bipartite graph $K_{m,n}$, we conclude this section by linking Theorem 3 to the results known in the area of max-weight coloring. It is known that an optimal max-weight edge coloring in an edge-weighted graph G can always be obtained using at most $2\varDelta -1$ colors, where $\varDelta$ is the maximum vertex degree of G, see for example Demange et al. (2002); de Werra et al. (2009). This bound is worse than the bound given in Theorem 3, as for a complete bipartite graph $G=K_{m,n}$ with $m<n$ we have $\varDelta =n$, and therefore $2\varDelta -1=n+n-1>n+m-1$. However, for the vertex coloring version of max-weight coloring on a vertex-weighted graph G, Demange et al. (2002) show that an optimal max-weight vertex coloring can be obtained using at most $\varDelta +1$ colors. Note that the max-weight edge coloring problem on a graph H can be seen viewed as the max-weight vertex coloring problem on the line graph $G=L(H)$ of H. Then, since the line graph of $K_{m,n}$ has maximum degree $\varDelta =n+m-2$, the bound $\varDelta +1$ on the number of colors needed yields $n+m-1$, which is equal to the maximum number of cycles stated in Theorem 3.

Fig. 3

An optimal schedule with 2m cycles, m of which are complete and m are incomplete

3 Scheduling with deadlines

In this section, we consider problem $O|synmv,C_{j}\le D_{j}|-$, where each job $J_{j}, 1\le j\le n$, has a given deadline $D_{j}$ by which it has to be completed. We prove that finding a feasible schedule with all jobs meeting their deadlines is NP-complete in the strong sense even if there are only two machines and each job has only one nonzero processing time. Furthermore, we show that problem $O2|synmv,C_{j}\le D_{j},D_{j}\in \{D^{\prime },D^{\prime \prime }\}|-$, where the set of all deadlines is limited to two values, is at least NP-complete in the ordinary sense. The proofs presented below are based on the ideas of Brucker et al. (1998) who established the complexity status of the parallel batching problem with deadlines.

Consider the 3-PARTITION problem (3-PART) known to be strongly NP-complete, cf. Garey and Johnson (1979). Given a set $Q=\{1,\ldots ,3q\}$, a bound E and natural numbers $e_{i}$ for every $i\in Q$, satisfying $\sum _{i\in Q}e_{i}=qE$ and $\frac{E}{4}<e_{i}<\frac{E}{2}$, can Q be partitioned into q subsets $Q_{k}, 1\le k\le q$, such that $\sum _{i\in Q_{k}}e_{i}=E$?

Based on an instance of 3-PART, we construct an instance I(q) of the two-machine synchronous open shop problem $O2|synmv,C_{j}\le D_{j}|-$ with $n=6q^2$ jobs, q deadlines and two machines, denoted by A and B. Each job $J_{j,l}$ has two indices j and l to distinguish between jobs of different types, $j=1,2,\ldots ,2q$ and $l=1,2,\ldots ,3q$. We introduce constants

$$\begin{aligned} T=\sum _{i=1}^{3q}i,\qquad T_{j}=\sum _{i=1}^{j}i,\qquad W=q^{3}E. \end{aligned}$$

For each $l, 1\le l\le 3q$, the processing times $a_{j,l}$ and $b_{j,l}$ of the jobs $J_{j,l}$ on machines A and B are defined as follows:

$$\begin{aligned} \begin{array}{lcl} a_{j,l}=lW+(q-j)e_{l}, &{} ~ &{} b_{j,l}=0 \text{ for } 1\le j\le q; \\ a_{q+1,l}=0, &{} ~ &{} b_{q+1,l}=lW+qe_{l}; \\ a_{j,l}=0, &{} ~ &{} b_{j,l}=lW \text{ for } q+2\le j\le 2q. \end{array} \end{aligned}$$

The deadlines $D_{j,l}$ are set to

$$\begin{aligned} \begin{array}{ll} D_{j,l}=jTW+(jq^{2}-T_{j}q+T_{j})E &{} \text{ for } 1\le j\le q; \\ D_{j,l}=qTW+(q^{3}-T_{q}q+T_{q})E &{} \text{ for } q+1\le j\le 2q. \end{array} \end{aligned}$$

Throughout the proof we use the following terms for different classes of jobs. Parameter $l, 1\le l\le 3q$, characterizes jobs of type l . For each value of l there are 2q jobs of type l, q of which have nonzero A-operations (we call these A-jobs) and the remaining q jobs have nonzero B-operations (we call these B-jobs). Among the q B-jobs of type l, there is one long B -job of type l, namely $J_{q+1,l}$ with processing time $lW+qe_{l}$, and there are $q-1$ short B-jobs of type l, namely $J_{q+2,l},J_{q+3,l},\ldots ,J_{2q,l}$, each with processing time lW. Overall, there are 3q long B-jobs, one of each type $l, 1\le l\le 3q$, and $3q\left( q-1\right)$ short B-jobs, with $q-1$ short jobs of each type l. Note that, independent of l, job $J_{j,l}$ is an A-job if $1\le j\le q$, and a B-job if $q+1\le j\le 2q$.

With respect to the deadlines, the jobs with nonzero B-operations are indistinguishable. The jobs with nonzero A-operations have deadlines $D_{j,l}$ depending on j; we refer to those jobs as component $_{j}$ A -jobs. For each j, there are 3q jobs of that type.

Fig. 4

Schedule derived from a solution to 3-PART

Lemma 1

If there exists a solution $Q_{1},Q_{2},\ldots ,Q_{q}$ to an instance of 3-PART, then there exists a feasible schedule for the instance I(q) of the two-machine synchronous open shop problem with q deadlines.

Proof

We construct a schedule $S^{*}$ consisting of q components $\varGamma _{1},\varGamma _{2},\ldots ,\varGamma _{q}$, each of which consists of 3q cycles, not counting zero-length cycles. In component $\varGamma _{k}, 1\le k\le q$, machine A processes 3q component$_{k}$ A-jobs, one job of each type $l, l=1,2,\ldots ,3q$. Machine B processes 3 long B-jobs and $3\left( q-1\right)$ short B-jobs, also one job of each type $l, l=1,2,\ldots ,3q$.

Within one component, every cycle combines an A-job and a B-job of the same type $l, 1\le l\le 3q$. The ordering of cycles in each component is immaterial, but component $\varGamma _{k}$ precedes component $\varGamma _{k+1}, 1\le k\le q-1$. If $Q_{k}=\left\{ l_{1},l_{2},l_{3}\right\}$ is one of the sets of the solution to 3-PART, then the three long B-jobs $J_{q+1,l_{1}}, J_{q+1,l_{2}},J_{q+1,l_{3}}$ are assigned to cycle $\varGamma _{k}$.

Finally, there are $3q^{2}$ cycles of length zero. We assume that each zero-length operation is scheduled immediately after the nonzero operation of the same job.

The resulting schedule $S^{*}$ is shown in Fig. 4.

It is easy to verify that if $Q_{1},Q_{2},\ldots ,Q_{q}$ define a solution to the instance of 3-PART, then the constructed schedule $S^{*}$ is feasible with all jobs meeting their deadlines. $\square$

We now prove the reverse statement. The proof is structured into a series of properties where the last one is the main result of the lemma.

Lemma 2

If there exists a feasible schedule S for the instance I(q) of the synchronous open shop problem with q deadlines, then the following properties hold : 

• (1) each cycle of nonzero length contains an A-job of type l and a B-job of the same type $l, l=1,2,\ldots ,3q$; without loss of generality we can assume that each zero-length operation is scheduled in the cycle immediately after the nonzero-length operation of the same job;

• (2) no component$_{j}$ A-job is scheduled on machine A before any component$_{i}$ A-job, with $1\le i\le j-1$; hence S is splittable into components $\varGamma _{1},\varGamma _{2},\ldots ,\varGamma _{q}$ in accordance with A-jobs;

• (3) each component $\varGamma _{j}, 1\le j\le q$, defines a set $Q_{j}$ of indices that correspond to long B-jobs scheduled in $\varGamma _{j}$; the resulting sets $Q_{1},Q_{2},\ldots ,Q_{q}$ define a solution to the instance of 3-PART.

Proof

(1) In a feasible schedule S satisfying the first property, all cycles have a balanced workload on machines A and B: in any component $\varGamma _{k}, 1\le k\le q$, the cycle lengths are W, 2W, ..., 3qW, with the value $qe_{l}$ or $(q-k)e_{l}$ added. Thus, the total length of such a schedule is at least $q\cdot TW$. For a schedule that does not satisfy the first property, the machine load is not balanced in at least two cycles, so that the lW-part of the processing time does not coincide in these cycles. Thus, the total length of such a schedule is at least $qTW+W=qTW+q^{3}E$. Since $q>1$, the latter value exceeds the largest possible deadline

$$\begin{aligned} \max _{1\le j\le 2q,1\le l\le 3q}\left\{ D_{j,l}\right\} =qTW+(q^{3}-T_{q}q+T_{q})E, \end{aligned}$$

a contradiction.

Note that the above especially shows that zero-length operations are only paired in cycles with other zero-length operations. Therefore, we can assume without loss of generality that zero-length operations are scheduled immediately after the nonzero-length operations of the same job. Indeed, if this is not the case, we can change the order of cycles, and possibly the assignment of zero-length operations to the zero-length cycles in order to achieve the assumed structure, without changing the feasibility of the schedule.

(2)  Consider a schedule S in which all component$_{u}$ A-jobs precede component$_{u+1}$ A-jobs for $u=1,2,\ldots ,i-1$, but after that a sequence of component$_{i}$ A-jobs is interrupted by at least one component$_{j}$ A-job with $j>i$. Let the very last component$_{i}$ A-job scheduled in S be $J_{i,v}$ for some $1\le v\le 3q$. Then the completion time of the cycle associated with $J_{i,v}$ is at least $iTW+W$, where TW is a lower bound on the total length of all component$_{u}$ A-jobs, $u=1,2,\ldots ,i$, and W is the smallest length of a cycle that contains the violating component$_{j}$ A-job. Since W is large, job $J_{i,v}$ does not meet its deadline

$$\begin{aligned} D_{i,v}=iTW+(iq^{2}-T_{i}q+T_{i})E, \end{aligned}$$

a contradiction.

The second property implies that on machine A all component$_{1}$ A-jobs are scheduled first, followed by all component$_{2}$ A-jobs, etc. Thus, the sequence of jobs on machine A defines a splitting of the schedule S into components $\varGamma _{1},\varGamma _{2},\ldots ,\varGamma _{q}$.

(3) Given a schedule S satisfying the first two properties, we first define sets $Q_{1},Q_{2},\ldots ,Q_{q}$ and then show that they provide a solution to 3-PART.

Schedule S consists of components $\varGamma _{j}, 1\le j\le q$. In each component $\varGamma _{j}$ machine A processes all component$_{j}$ A-jobs $J_{j,l} (1\le l\le 3q)$, each of which is paired with a B-job of the same type l. Recall that a B-job $J_{q+1,l}$ of type l is long, with processing time $lW+qe_{l}$. All other B-jobs $J_{j,l}, q+2\le j\le 2q$, of type l are short, with processing time lW. Considering the long B-jobs of component $\varGamma _{j}$, define a set $Q_{j}$ of the associated indices, i.e., $l\in Q_{j}$ if and only if the long B-job $J_{q+1,l}$ is scheduled in component $\varGamma _{j}$. Denote the sum of the associated numbers in $Q_{j}$ by $e(Q_{j}):=\sum _{l\in Q_{j}}e_{l}$.

The length of any cycle in component $\varGamma _{j}$ is either $a_{j,l}=lW+(q-j)e_{l}$ if the component$_{j}$ A-job of type l is paired with a short B-job of type l, or $b_{q+1,l}=lW+qe_{l}$ if it is paired with the long B-job $J_{q+1,l}$. Then the completion time $C_{\varGamma _{j}}$ of component $\varGamma _{j}, 1\le j\le q$, can be calculated as

$$\begin{aligned} C_{\varGamma _{j}}= & {} \sum _{h=1}^{j}\left( \sum _{l\in Q_{h}} [ lW+qe_{l}] +\sum _{l\in Q\setminus Q_{h}} [ lW+(q-h)e_{l}] \right) \\= & {} \sum _{h=1}^{j}(TW+(q-h)qE+he(Q_{h})), \end{aligned}$$

which for a feasible schedule S does not exceed the common deadline $D_{j,l}$ of A-jobs in component $\varGamma _{j}, D_{j,l}=jTW+jq^{2}E-T_{j}qE+T_{j}E=\sum _{h=1}^{j}\left( TW+(q-h)qE+hE\right) .$ Notice that the deadline of any B-job in component $\varGamma _{j}$ is not less than $D_{j,l}$.

Thus, for any $j, 1\le j\le q$ we get

$$\begin{aligned}&D_{j,l}-C_{\varGamma _{j}} =\sum _{h=1}^{j}\left( TW+(q-h)qE+hE\right) \nonumber \\&\qquad -\sum _{h=1}^{j}\left( TW+(q-h)qE+he(Q_{h})\right) \nonumber \\&\quad =\sum _{h=1}^{j}h\left( E-e(Q_{h})\right) \ge 0. \end{aligned}$$

(8)

If all inequalities in (8) hold as equalities, i.e.,

$$\begin{aligned} \sum _{h=1}^{j}h\left( E-e(Q_{h})\right) =0,\quad j=1,2,\ldots ,q, \end{aligned}$$

then it is easy to prove by induction that $E-e(Q_{h}) =0$ for each $h=1, \ldots , q$ and therefore the partition $Q_{1}, Q_{2}, \ldots , Q_{q}$ of Q defines a solution to 3-PART.

Assume the contrary, i.e., there is at least one strict inequality in (8). Then a linear combination L of inequalities (8) with strictly positive coefficients has to be strictly positive. Using coefficients $\frac{1}{j}-\frac{1}{j+1}$ for $j=1,2,\ldots ,q-1$ and $\frac{1 }{q}$ for $j=q$ we obtain:

$$\begin{aligned} L&=\sum _{j=1}^{q-1}\left[ \left( \frac{1}{j}-\frac{1}{j+1}\right) \sum _{h=1}^{j}h\left( E-e(Q_{h})\right) \right] \\&\quad +\frac{1}{q} \sum _{h=1}^{q}h\left( E-e(Q_{h})\right) >0. \end{aligned}$$

It follows that

$$\begin{aligned} 0 < L= & {} \sum _{h=1}^{q-1}\left[ h\left( E-e(Q_{h})\right) \sum _{j=h}^{q-1}\left( \frac{1}{j}-\frac{1}{j+1}\right) \right] \\&+\frac{1}{q}\sum _{h=1}^{q}h\left( E-e(Q_{h})\right) \\= & {} \sum _{h=1}^{q-1}\left[ h\left( E-e(Q_{h})\right) \left( \frac{1}{h}-\frac{1}{q}\right) \right] \\&+ \frac{1}{q}\sum _{h=1}^{q}h\left( E-e(Q_{h})\right) \\= & {} \sum _{h=1}^{q}\left( E-e(Q_{h})\right) =0, \end{aligned}$$

where the last equality follows from the definition of E for an instance of 3-PART. The obtained contradiction proves the third property of the lemma. $\square$

Lemmas 1 and 2 together imply the following result.

Theorem 4

Problem $O2|synmv,C_{j}\le D_{j}|-$ is NP-complete in the strong sense, even if each job has only one nonzero operation.

Similar arguments can be used to formulate a reduction from the PARTITION problem (PART) to the two-machine synchronous open shop problem, instead of the reduction from 3-PART. Notice that in the presented reduction from 3-PART all B-jobs have the same deadline, while A-jobs have q different deadlines, one for each component $\varGamma _{j}$ defining a set $Q_{j}$ . In the reduction from PART we only require two different deadlines $D,D^{\prime }$, one for each of the two sets corresponding to the solution to PART. Similar to the reduction from 3-PART, we define component$_{1}$ A-jobs with deadline D and component$_{2}$ A-jobs with deadline $D^{\prime }$ which define a splitting of the schedule into two components $\varGamma _{1},\varGamma _{2}$. For each of the natural numbers of PART we define one long B-job and one short B-job and show that the distribution of the long jobs within the two components of the open shop schedule corresponds to a solution of PART. Omitting the details of the reduction, we state the following result.

Theorem 5

Problem $O2|synmv,C_{j}\le D_{j},D_{j}\in \{ D^{\prime },D^{\prime \prime }\} |-$ with only two different deadlines is at least ordinary NP-complete, even if each job has only one nonzero operation.

At the end of this section we note that the complexity of the relaxed versions of the problems, which allow incomplete cycles modeled via dummy jobs, remains the same as stated in Theorems 4 and 5. Indeed, Property 1 of Lemma 2 stating that each nonzero operation of some job is paired with a nonzero operation of another job, still holds for the version with dummy jobs. Therefore, in the presence of dummy jobs a schedule meeting the deadlines has the same component structure as in Lemmas 1 and 2, so that the same reduction from 3-PART (PART) works for proving that $O2|synmv,rel,C_{j}\le D_{j}|-$ is strongly NP-complete and $O2|synmv,rel,C_{j}\le D_{j},D_{j}\in \left\{ D^{\prime },D^{\prime \prime }\right\} |-$ is at least ordinary NP-complete.

4 Minimizing the total completion time

In this section, we prove that the synchronous open shop problem with the total completion time objective is strongly NP-hard even in the case of $m=2$ machines. The proof uses some ideas by Röck (1984) who proved NP-hardness of problem $F2|no-wait|\sum C_{j}$. Note that the latter problem is equivalent to the synchronous flow shop problem $F2|synmv|\sum C_{j}$.

For our problem $O2|synmv|\sum C_{j}$ we construct a reduction from the auxiliary problem AUX, which can be treated as a modification of the HAMILTONIAN PATH problem known to be NP-hard in the strong sense (Garey and Johnson 1979).

Consider the HAMILTONIAN PATH problem defined for an arbitrary connected graph $G^{\prime }=(V^{\prime },E^{\prime })$ with $n-1$ vertices $V^{\prime }=\{1,2,\ldots ,n-1\}$ and edge set $E^{\prime }$. It has to be decided whether a path exists which visits every vertex exactly once. To define the auxiliary problem AUX, we introduce a directed graph $\overrightarrow{G}$ obtained from $G^{\prime }$ in two stages:

• first add to $G^{\prime }$ a universal vertex 0, i.e., a vertex connected by an edge with every other vertex; denote the resulting graph by $G=(V,E)$;

• then replace each edge of graph G by two directed arcs in opposite directions; denote the resulting directed graph by $\overrightarrow{G}=(V, \overrightarrow{E})$.

For problem AUX it has to be decided whether an Eulerian tour $\epsilon$ in $\overrightarrow{G}$ starting and ending at 0 exists where the last n vertices constitute a Hamiltonian path, ending at 0. As shown in Appendix 2, the two problems HAMILTONIAN PATH and AUX have the same complexity status. An example that illustrates graphs $G^{\prime }, G$ and $\overrightarrow{G}$ is shown in Fig. 5; a possible Eulerian tour in $\overrightarrow{G}$ is $\epsilon =(0,1,0,2,0,3,0,4,2,4,3,2$, ), where the last $n=5$ vertices form a Hamiltonian path.

Fig. 5

Constructing the graph $\overrightarrow{G}$ for problem AUX

Given an instance of AUX with n vertices $V=\{0,1,\ldots ,n-1\}$ and arcs $\overrightarrow{E}$, we introduce an instance of the synchronous open shop problem SO using the constants

$$\begin{aligned} \sigma =|\overrightarrow{E}|/2, \ K =8n, \ \xi =4K\sigma ^{2}, \ L=2n^9\xi . \end{aligned}$$

Furthermore, for each vertex $v\in V$ let $d(v)=\deg ^{-}(v)=\deg ^{+}(v)$ be the in-degree $\deg _{\overrightarrow{G}}^{-}(v)$ (the number of arcs entering v), which here equals its out-degree $\deg _{\overrightarrow{G}}^{+}(v)$ (the number of arcs leaving v). Note that $\sigma =\sum _{v\in V^{\prime }} d(v)/2$.

In a possible solution to AUX, if one exists, every vertex $v\in V\backslash \{0\}$ has to be visited d(v) times and each arc $(v,w)\in \overrightarrow{E}$ has to be traversed exactly once. We introduce instance SO for problem $O2|synmv|\sum C_{j}$. For each vertex v we create d(v) vertex-jobs $\text {Ve}_{v}^{1},\text {Ve}_{v}^{2},\ldots ,\text {Ve}_{v}^{d(v)}$, one for each visit of vertex v in an Eulerian tour $\epsilon$, and for each arc (v, w) we create an arc-job $\hbox {Ar}_{vw}$. For vertex $v=0$ we create d(0) vertex-jobs, as described, and additionally one more vertex-job $\hbox {Ve}_{0}^{0}$ that corresponds to the origin of the Eulerian tour $\epsilon$. In addition to these $2\sigma +1$ vertex-jobs and $2\sigma$ arc-jobs, we create $2n^{9}+1$ “forcing” jobs $F_{0},F_{1},\ldots ,F_{2n^{9}}$ to achieve a special structure of a target schedule. We denote the set of jobs N. Their processing times are given in Table 1.

Table 1 Processing times of the jobs in instance SO

We call each operation with a processing time of L a “long operation” and each operation with a processing time of less than L a “short operation.” Further, we refer to a job as a long job if at least one of its operations is long and as a short job if both of its operations are short.

The threshold value of the objective function is defined as $\varTheta =\varTheta _{1}+\varTheta _{2}$, where

$$\begin{aligned} \varTheta _{1}= & {} (8\sigma ^{2}+2\sigma )\xi +4\sigma ^{2}K-2\sum _{v\in V} vd(v)+n^{2}, \\ \varTheta _{2}= & {} 2(n^{9}+1)\left( \left( n^{9}+1\right) L+4\sigma \xi +2\sigma K+n\right) . \end{aligned}$$

As we show later, in a schedule with $\sum C_{j}\le \varTheta$, the total completion time of the short jobs is $\varTheta _{1}$ and the total completion time of the long jobs is $\varTheta _{2}$.

Theorem 6

Problem $O2|synmv|\sum C_{j}$ is strongly NP-hard.

Proof

Consider an instance AUX and the corresponding scheduling instance SO. We prove that an instance of problem AUX has a solution, if and only if the instance SO has a solution with $\sum C_{j}\le \varTheta$.

“$\Rightarrow$”: Let the solution to AUX be given by an Eulerian tour $\epsilon =\left( v_{0},v_{1},\ldots ,v_{2\sigma }\right)$ starting at $v_{0}=0$ and ending at $v_{2\sigma }=0$ such that the last n vertices form a Hamiltonian path. The solution to problem SO consists of two parts and it is constructed as follows:

• In Part 1, machine $M_{1}$ processes $2\sigma +1$ vertex-jobs and $2\sigma$ arc-jobs in the order that corresponds to traversing $\epsilon$. Machine $M_{2}$ starts with processing the forcing job $F_{0}$ in cycle 1 and then proceeds in cycles $2, 3, \ldots , 4\sigma +1$ with the same sequence of vertex-jobs and arc-jobs as they appear in cycles $1, 2, \ldots , 4\sigma$ on machine $M_{1}$. Notice that in Part 1 all vertex- and arc-jobs are fully processed on both machines except for job $\hbox {Ve}_{0}^{d(v)}$ which is processed only on $M_{1}$ in the last cycle $4\sigma +1$.

• In Part 2, machine $M_{1}$ processes the forcing jobs $F_{0}, F_{1}, \ldots , F_{2n^{9}}$ in the order of their numbering. Machine $M_{2}$ processes in the first cycle of Part 2 (cycle $4\sigma +2$ ) the vertex-job $\hbox {Ve}_{0}^{d(v)}$ which is left from Part 1. Then in the remaining cycles $4\sigma +3, \ldots , 4\sigma +2+2n^{9}$, every job $F_{i} (i=1,\ldots ,2n^{9})$ on $M_{1}$ is paired with job $F_{i+1}$ on $M_{2}$ if i is odd, and with job $F_{i-1}$, otherwise.

Fig. 6

An optimal solution to SO

In Fig. 6 we present an example of the described schedule based on graph $\overrightarrow{G}$ of Fig. 5. Notice that there are $n=5$ vertices in $\overrightarrow{G}$, and parameter $\sigma$ equals 8. Traversing the Eulerian tour $\epsilon =(0,1,0,2,0,3,0,4,2,4,3,2$, ) incurs the sequence of vertex-jobs and arc-jobs $(\hbox {Ve}_{0}^{0}, \hbox {Ar}_{01}, \hbox {Ve}_{1}^{1}, \hbox {Ar}_{10}, \hbox {Ve}_{0}^{1}, \hbox {Ar}_{02}, \ldots , \hbox {Ve}_{1}^{2}, \hbox {Ar}_{12}, \hbox {Ve}_{2}^{4}, \hbox {Ar}_{23}, \hbox {Ve}_{3}^{3}, \hbox {Ar}_{34}, \hbox {Ve}_{3}^{4}, \hbox {Ar}_{40}, \hbox {Ve}_{0}^{4})$. There are $2\sigma +1=17$ vertex-jobs, $2\sigma =16$ arc-jobs, and $2n^{9}+1=2 \times 5^{9}+1$ jobs $F_i$, so that all jobs are allocated in $34+2\times 5^{9}$ cycles. The schedule is represented as a sequence of cycles, where the operations on machines $M_{1}$ and $M_{2}$ are enframed and the lengths of the corresponding operations are shown above or below. Operations of equal length in one cycle are shown as two boxes of the same length; the sizes of the boxes of different cycles are not to scale.

We demonstrate that the constructed schedule satisfies $\sum C_{j}=\varTheta$. Observe that most cycles have equal workload on both machines, except for the n cycles that correspond to the vertex-jobs of the Hamiltonian path; in each such cycle the operation on $M_{1}$ is one unit longer than the operation on $M_{2}$.

First consider the short jobs. The initial vertex-job $\hbox {Ve}_{0}^{0}$ that corresponds to the origin $v_{0}=0$ of $\epsilon =\left( v_{0},v_{1},\ldots ,v_{2\sigma }\right)$ completes at time $\xi$. Each subsequent vertex-job that corresponds to $v_{i}, 1\le i\le 2\sigma -n$, where we exclude the last n vertices of the Hamiltonian path, completes at time $(2i+1)\xi +iK$. Consider the next $n-1$ vertex-jobs $v_{i}$ with $2\sigma -n+1\le i\le 2\sigma -1$ (excluding the very last vertex-job $\hbox {Ve}_{0}^{d(0)}$ as it is a long job); every such job $v_{i}$ completes at time $(2i+1)\xi +iK+(n+i-2\sigma )$.

The remaining short jobs correspond to arc-jobs. The completion time of the i-th arc-job $\text {Ar}_{v_{i-1}v_{i}}$ is $2i\xi +iK-2v_{i}$ for $1\le i\le 2\sigma -n$ and $2i\xi +iK-2v_{i}+(n+i-2\sigma )$ for $2\sigma -n+1\le i\le 2\sigma$.

Thus, the total completion time of all short jobs sums up to

$$\begin{aligned}&\xi +\sum _{i=1}^{2\sigma -n}\left[ (2i+1)\xi +iK\right] \\&\qquad +\sum _{i=2\sigma -n+1}^{2\sigma -1}\left[ (2i+1)\xi +iK+(n+i-2\sigma )\right] \\&\qquad +\sum _{i=1}^{2\sigma -n}\left[ 2i\xi +iK-2v_{i}\right] \\&\qquad +\sum _{i=2\sigma -n+1}^{2\sigma }\left[ 2i\xi +iK-2v_{i}+(n+i-2\sigma )\right] \\&\quad =\left[ \xi +\sum _{i=1}^{2\sigma -1}(2i+1)\xi +\sum _{i=1}^{2\sigma }2i\xi \right] \\&\qquad +\left[ \sum _{i=1}^{2\sigma -1}iK+\sum _{i=1}^{2\sigma }iK\right] +\left[ \sum _{i=1}^{n-1}i+\sum _{i=1}^{n}i\right] -2\sum _{i=1}^{2\sigma }v_{i} \\&\quad =(8\sigma ^{2}+2\sigma )\xi +4\sigma ^{2}K+n^{2}-2\sum _{v\in V} vd(v) =\varTheta _{1}. \end{aligned}$$

Here we have used the equality

$$\begin{aligned} \sum _{i=1}^{2\sigma }v_{i}=\sum _{v\in V}vd(v) \end{aligned}$$

which holds for the Eulerian tour $\epsilon =\left( v_{0},v_{1},\ldots ,v_{2\sigma }\right)$ with $v_{i}\in V$.

Next, consider the completion times of the long jobs. The second operations of jobs $\hbox {Ve}_0^{d(0)}$ and $F_0$ appear in cycle $4\sigma +2$; all other long operations are scheduled in cycles $4\sigma +3, \ldots , 4\sigma +2 +2n^{9}$. There is a common part of the schedule, with cycles $1, 2, \ldots , 4\sigma +1$ that contributes to the completion time of every long job; the length of that common part is

$$\begin{aligned} \varDelta =4\sigma \xi +2\sigma K+n. \end{aligned}$$

Then the first two long jobs, $F_{0}$ and $\text {Ve}_{0}^{d(0)}$, are both completed at time $\varDelta +L$ and for $i=1,\ldots ,n^{9}$ the completion time of each pair of jobs $F_{2i-1}$ and $F_{2i}$ is $\varDelta +(2i+1)L$. Thus, the total completion time of the long jobs sums up to

$$\begin{aligned}&2\left( \varDelta +L\right) +2\sum _{i=1}^{n^{9}}\left[ \varDelta +(2i+1)L\right] \end{aligned}$$

(9)

$$\begin{aligned}&\quad =2\varDelta (n^{9}+1)+2(n^{9}+1)^{2}L \end{aligned}$$

(10)

$$\begin{aligned}&\quad =2(n^{9}+1)[( 4\sigma \xi +2\sigma K+n)+(n^{9}+1) L] =\varTheta _{2}\nonumber \\ \end{aligned}$$

(11)

and therefore the total completion time sums up to $\varTheta =\varTheta _{1}+\varTheta _{2}$.

“$\Leftarrow$”: Now we prove that if an instance of AUX does not have a solution, then also SO does not have a solution with $\sum C_{j}\le \varTheta$. Suppose to the contrary that there exists a schedule with $\sum C_{j}\le \varTheta$ and let S be an optimal schedule.

Fig. 7

Structure of schedule S

Such a schedule satisfies the following structural properties, see Appendix 2 for a proof.

• 1. In each cycle in S, both operations are either short or long.

• 2. All long operations are scheduled in the last $2n^{9}+1$ cycles. This defines the splitting of schedule S into Parts 1 and 2, with cycles $1, 2, \ldots , 4\sigma +1$ and $4\sigma +2, \ldots , 4\sigma +2+2n^{9}$.

• 3. The sum of completion times of all long jobs is at least $\varTheta _{2}$.

• 4. In S, machine $M_{1}$ operates without idle times.

• 5. In Part 1 of S, job $\hbox {Ve}_{0}^{0}$ is processed in the first two cycles which are of the form

  

  , where

  

  represents a short operation. While the order of these two cycles is immaterial, without loss of generality we assume that

  

  precedes

  

  ; otherwise the cycles can be swapped without changing the value of $\sum C_{j}$.

• 6. The two operations of each vertex-job and the two operations of each arc-job are processed in two consecutive cycles, first on $M_{1}$ and then on $M_{2}$.

• 7. In Part 1 of S, machine $M_{1}$ alternates between processing arc-jobs and vertex-jobs. Moreover, an operation of a vertex-job corresponding to v is followed by an operation of an arc-job corresponding to an arc leaving v. Similarly, an operation of an arc-job for arc (v, w) is followed by an operation of a vertex-job for vertex w. By Property 6, the same is true for machine $M_{2}$ in Part 1 and in the first cycle that follows it.

• 8. The first arc-job that appears in S corresponds to an arc leaving 0. Among the vertex-jobs, the last one is $\text {Ve}_{0}^{d(0)}$.

Using the above properties we demonstrate that if problem AUX does not have a solution, then the value of $\sum C_{j}$ in the optimal schedule S exceeds $\varTheta$. Due to Property 3 it is sufficient to show that the total completion time $\sum _{j=1}^{\mu }C_{j}$ of all short jobs exceeds $\varTheta _{1}$. Let us assume that $\{1,2,\ldots ,\mu \}$ with $\mu =4\sigma$ are the short jobs of the instance SO. This set consists of $2\sigma$ short vertex-jobs (the long vertex-job $\hbox {Ve}_{0}^{d(0)}$ is excluded) and $2\sigma$ arc-jobs.

Properties 1–2 allow the splitting of S into two parts. Part 2 plays an auxiliary role. Part 1 is closely linked to problem AUX.

The sequence of arc- and vertex-jobs in Part 1 of S defines an Eulerian tour in $\overrightarrow{G}$. Indeed, all arc-jobs appear in S and by Property 7 the order of the arc- and vertex-jobs in S defines an Eulerian trail in $\overrightarrow{G}$. Since for every vertex v, its in-degree equals its out-degree, an Eulerian trail must be an Eulerian tour. Denote it by $\epsilon =\left( v_{0},v_{1},\ldots ,v_{2\sigma }\right)$. Due to Property 8 and by the assumption of Property 5 the Eulerian tour $\epsilon$ starts and ends at $v_0=0$.

In Fig. 7 we present the structure of Part 1 of schedule S, where $\hbox {Ve}_{v}^{*}$ represents one of the vertex-jobs $\hbox {Ve}_{v}^{1}$, $\hbox {Ve}_{v}^{2}$,..., $\hbox {Ve}_{v}^{d(v)}$, with processing time $\xi +K-2v+1$ or $\xi +K-2v$ on machine $M_{1}$, depending on whether the upper index is d(v) or a smaller number. Part 2 is as in the proof of “ $\Rightarrow$”.

Notice that all operations of the short jobs appear only in Part 1 of the above schedule, with one short job completing in each cycle $2, 3,\ldots , \mu +1$. In each cycle of Part 1, both operations are of the same length, except for the $n-1$ cycles where the vertex-jobs $\hbox {Ve}_{v}^{d(v)}$, $v\in \{1,2,\ldots ,n-1\}$, are scheduled on machine $M_{1}$, and the final cycle of Part 1 where $\hbox {Ve}_{0}^{d(0)}$ is scheduled. In these cycles the operation on $M_{1}$ is one unit longer than the operation on $M_{2}$. Let

$$\begin{aligned} \vartheta :=\left\{ \text {Ve}_{v}^{d(v)}~|~v=1,2,\ldots ,n-1\right\} \end{aligned}$$

be the set of the $n-1$ jobs with one extra unit of processing. Job $\hbox {Ve}_{0}^{d(0)}$ is not included in this set as its precise location is known by Property 8.

We show that for any Eulerian tour $\epsilon =\left( v_{0},v_{1},\ldots ,v_{2\sigma }\right)$, the value of $\sum _{j=1}^{\mu }C_{j}$ does not depend on the order of the vertices in $\epsilon$; it only depends on the positions of the $n-1$ jobs from $\vartheta$. In particular, we demonstrate that

$$\begin{aligned} \sum _{j=1}^{\mu }C_{j}=\varUpsilon +\sum _{\ell =2}^{\mu +1}\left( \mu -\ell +2\right) x_{\ell }, \end{aligned}$$

(12)

where $\varUpsilon =\varTheta _{1}-n^{2}$ is a constant, and $x_{\ell }\in \{0,1\}$ indicates whether some job from $\vartheta$ is allocated to cycle $\ell$ or not.

Table 2 Summary of the results

The constant term $\varUpsilon$ is a lower bound estimate for $\sum _{j=1}^{\mu }C_{j}$ obtained under the assumption that one additional time unit for each job from $\vartheta$ and also for job $\hbox {Ve}_{0}^{d(0)}$ is ignored. If we drop “$+1$” from the input data of the instance SO, then both machines have equal workload in every cycle. Job $\hbox {Ve}_{0}^{0}$ contributes $\xi$ to $\varUpsilon$. The job corresponding to $v_{i}$, except for job $\text {Ve}_{0}^{d(0)}$ (which is a long job) contributes $(2i+1)\xi +iK$. The arc-job corresponding to $\left( v_{i},v_{i+1}\right)$ contributes $2i\xi +iK-2v_{i+1}$. Thus,

$$\begin{aligned} \varUpsilon= & {} \xi +\sum _{i=1}^{2\sigma -1}\left[ (2i+1)\xi +iK\right] +\sum _{i=1}^{2\sigma }\left[ 2i\xi +iK-2v_{i+1}\right] \\= & {} (8\sigma ^{2}+2\sigma )\xi +4\sigma ^{2}K-2\sum _{v\in V}vd(v)=\varTheta _{1}-n^{2}. \end{aligned}$$

Consider now the effect of the additional time unit on machine $M_{1}$ for each job from $\vartheta$ and for job $\hbox {Ve}_{0}^{d(0)}$. If some $\vartheta$-job is allocated to a cycle $\ell$, then the additional unit of processing increases by one the completion time of every short job finishing in cycles $\ell , \ell +1, \ldots , \mu +1$, and thus contributes $\left( \mu +1\right) -\ell +1$ to $\sum _{j=1}^{\mu }C_{j}$. This justifies formula (12).

As shown in the above template, each of the $n-1$ jobs $j\in \vartheta$ can be scheduled in any odd-numbered cycle $\ell \in \left\{ 3,5,\ldots ,\mu -1\right\}$. Also, by Property 8, an additional time unit appears in cycle $\mu +1$ due to the allocation of $\hbox {Ve}_{0}^{d(0)}$ to machine $M_{1}$, which affects the completion time of a short job in that cycle. Thus, the minimum value of $\sum _{j=1}^{\mu }C_{j}$ is achieved if all $n-1$ jobs from $\vartheta$ are allocated to the latest possible odd-numbered positions, i.e., to positions $\ell =\left( \mu -1\right) -2i$ for $i=0,1,\ldots ,n-2$. Together with an extra “1 ” related to the allocation of $\hbox {Ve}_{0}^{d(0)}$ to cycle $\mu +1$, this results in

$$\begin{aligned}&\sum _{\ell =2}^{\mu +1}\left( \mu -\ell +2\right) x_{\ell }=1+\sum _{i=0}^{n-2}\left[ \mu -\left( \mu -1-2i\right) +2\right] \\&=1+3+\cdots +\left( 2n-1\right) =n^{2}, \end{aligned}$$

so that $\sum _{j=1}^{\mu }C_{j}$ is equal to $\varTheta _{1}$ if jobs $\vartheta$ are allocated to the latest feasible positions. Due to (12), any other allocation of jobs $\vartheta$, which does not involve the last $n-1$ odd-numbered positions, results in a larger value of $\sum _{j=1}^{\mu }C_{j}$.

By the main assumption of the part “$\Leftarrow$”, AUX does not have a solution where the last n vertices form a Hamiltonian path. Therefore, the last n vertices of any Eulerian tour $\epsilon =\left( v_{0},v_{1},\ldots ,v_{2\sigma }\right)$ have at least two occurrences of the same vertex v and therefore in the associated schedule, among the last n vertex-jobs there are at least two vertex-jobs $\hbox {Ve}_{v}^{i}, \hbox {Ve}_{v}^{j}$ associated with v. Thus, it is impossible to have $n-1$ jobs from $\vartheta$ allocated to the last $n-1$ odd-numbered cycles and to achieve the required threshold value $\varTheta _{1}$. $\square$

At the end of this section we observe that the proof of Properties 1–8 can be adjusted to handle the case with dummy jobs. Indeed, in an optimal solution of the instance, even if we allow dummy jobs, dummy operations are not allowed to be paired with actual operations of nonzero length (see Property 4). We conclude therefore that the complexity status of the relaxed problem is the same as that for the standard one.

Theorem 7

Problem $O2|synmv, rel| \sum C_j$ is strongly NP-hard.

5 Conclusions

In this paper we studied synchronous open shop scheduling problems. The results are summarized in Table 2. Note that the polynomial time results in lines 2 and 3 do not include presorting of all jobs.

All results from Table 2 also hold for the relaxed versions of the scheduling problems, in which cycles may consist of less than m jobs.

For problem $O2|synmv|C_{\max }$ we proved a new structural property, namely the small block property. Using it, we formulated a much easier solution algorithm than previously known. Unfortunately, we were unable to prove an improved structural property for any fixed $m>2$. In Table 2 we quote a previously known algorithm, which is based on the corridor property. Our result for two machines gives hope that this general result for fixed m may also be improved and highlights possible approaches for such an improvement.

The NP-completeness results of Sect. 3 imply that if instead of hard deadlines $D_{j}$ soft due dates $d_{j}$ are given (which are desirable to be met, but can be violated), then the corresponding problems O|synmv|f with the traditional regular due date-related objectives f such as the maximum lateness $L_{\max }=\max _{1\le j\le n}\{C_{j}-d_{j}\}$, the number of late jobs $\sum _{j=1}^{n}U_{j}$, or the total tardiness $\sum _{j=1}^{n}T_{j}$ are NP-hard, even if there are only two values of the due dates, $d_{j}\in \{d,d^{\prime }\}$. The corresponding problems become strongly NP-hard in the case of arbitrary due dates $d_{j}$.

Finally, due to the symmetry known for problems with due dates $d_{j}$ and those with release dates $r_{j}$, we conclude that problem $O2|synmv,r_{j}|C_{\max }$ is also strongly NP-hard and remains at least ordinary NP-hard if there are only two different values of release dates for the jobs.

In Sect. 4 we show that $O2|synmv|\sum C_{j}$ and its relaxed version are strongly NP-hard. Thus, due to the reducibility between scheduling problems with different objectives, the open shop problem with synchronization is NP-hard for any traditional scheduling objective function, except for $C_{\max }$.

Overall the synchronized version of the open shop problem appears to be no harder than the classical version, with two additional positive results for it: 1) $Om|synmv|C_{\max }$ is polynomially solvable for any fixed m while $Om||C_{\max }$ is NP-hard for $m\ge 3$ (Gonzalez and Sahni 1976); 2) $O|synmv,n=n'|C_{\max }$ is polynomially solvable for any fixed number of jobs $n'$ (due to the symmetry of jobs and machines), while $O|n= n^{\prime }|C_{\max }$ is NP-hard for $n^{\prime } \ge 3$. Moreover, in a solution to $O|synmv|C_{\max }$ with $n\le m$ all jobs have the same completion time, so that an optimal schedule for $C_{\max }$ is also optimal for any other nondecreasing objective f. It follows that we can solve problem $O|synmv, n=n'|f$, with a fixed number of jobs $n'$, for any such objective f.

Finally, comparing the open shop and flow shop models with synchronization, we also observe that the open shop problem is no harder, with a positive result for $Om|synmv|C_{\max }$ with an arbitrary fixed number of machines m , while its flow shop counterpart $Fm|synmv|C_{\max }$ is NP-hard for $m\ge 3$, see Waldherr and Knust (2015).

Appendices

Appendix 1: The proof of the small block property (Theorem 1)

The general idea of the proof can be described as follows. Starting with an arbitrary optimal solution which does not satisfy the small block property, replace repeatedly each block of size $s\ge 4$ by two blocks of cumulative size s, one of which is small. The replacement is performed for the relaxed problem $\mathrm {AP}_{\mathcal {F=}\emptyset }$, ignoring forbidden pairs ${{\mathcal {F}}}$, but making sure that the cost of the new solution (possibly infeasible in terms of ${{\mathcal {F}}}$) is not larger than that of its predecessor. Additionally, we keep 0-entries on the main diagonal unchanged, so that no new blocks of size 1 are created. As a result a new solution is constructed, feasible for $\mathrm {AP}_{\mathcal {F=}\emptyset }$ , of no higher cost than the original one, consisting of small blocks only. If the constructed solution is infeasible for $\mathrm {AP}_{{{\mathcal {F}}}}$, then at the next stage infeasible blocks of size 2 and 3 are replaced by feasible blocks, also without increasing the cost, achieving an optimal solution consisting of small blocks.

First we prove the possibility of block splitting (Lemma 3), and then explain how infeasible blocks can be converted into feasible ones (Lemmas 4, 5 for blocks of size 2 and 3, respectively). It leads to the main result (Theorem 1) - the existence of an optimal solution consisting of small blocks of type (6).

For a block consisting of 1-entries in rows and columns $\left\{ j_{1},j_{1}+1,\ldots ,j_{1}+s-1\right\}$, renumber those rows and columns as $\left\{ j_{1},j_{2},\ldots ,j_{s}\right\}$ with $j_{i}=j_{1}+i-1, 1\le i\le s$. The cost associated with block $\mathbf {X}_{h}$ is defined as

$$\begin{aligned} w\left( \mathbf {X}_{h}\right) =\sum _{u=1}^{s}\sum _{v=1}^{s}w_{j_{u}j_{v}}x_{j_{u}j_{v}}, \end{aligned}$$

so that the total cost of solution $\mathbf {X}$ with blocks (5) is

$$\begin{aligned} w\left( \mathbf {X}\right) =\sum _{h=1}^{z}w\left( \mathbf {X}_{h}\right) . \end{aligned}$$

Lemma 3

If an optimal solution to problem $\mathrm {AP}_{{{\mathcal {F}}}}$ contains a block $\mathbf {X}_{y}$ of size $s>3$, defined over rows and columns $\left\{ j_{1},j_{2},\ldots ,j_{s}\right\}$, then without increasing the cost it can be replaced by two blocks, one block of size 2 or 3 defined over rows and columns $\left\{ j_{1},j_{2}\right\}$ or $\left\{ j_{1},j_{2},j_{3}\right\}$, and one block defined over the remaining rows and columns. Furthermore, if a diagonal entry $x_{j_{k}j_{k}}$ in the initial solution is 0, then in the modified solution $x_{j_{k}j_{k}}$ is 0 as well.

Proof

Given a solution, we identify the nonzero entries in columns $j_{1}, j_{2}$, and $j_{3}$, and denote the corresponding rows by $j_{a}, j_{b}, j_{c}$. For these indices we have

$$\begin{aligned} x_{j_{a}j_{1}}=1,\qquad x_{j_{b}j_{2}}=1,\qquad x_{j_{c}j_{3}}=1. \end{aligned}$$

(13)

Furthermore, for nonzero entries in rows $j_{1}, j_{2}$, and $j_{3}$, we denote the corresponding columns by $j_{t}, j_{u}, j_{v}$ and have

$$\begin{aligned} x_{j_{1}j_{t}}=1,\qquad x_{j_{2}j_{u}}=1,\qquad x_{j_{3}j_{v}}=1. \end{aligned}$$

(14)

The proof is presented for the case

$$\begin{aligned} x_{j_{1}j_{1}}=x_{j_{2}j_{2}}=x_{j_{3}j_{3}}=0. \end{aligned}$$

(15)

Notice that the case $x_{j_{1},j_{1}}=1$ contradicts the assumption that block $\mathbf {X}_{y}$ is large. In the case of $x_{j_{2}j_{2}}=1$ we replace block $\mathbf {X}_{y}$ by block $\mathbf {X}_{y}^{\prime }$ as shown in Fig. 8. Here the 1-entries which are subject to change are enclosed in boxes and * denotes an arbitrary entry, 0 or 1. This transformation involves 4 entries in rows $\left\{ j_{1},j_{2}\right\}$ and columns $\left\{ j_{2},j_{t}\right\}$. Notice that the marked 1-entries in the initial block $\mathbf {X}_{y}$ belong to a diagonal of type $\diagup$, while the marked 1-entries in the resulting block $\mathbf {X}_{y}^{\prime }$ belong to a diagonal of type $\diagdown$, so that $w\left( \mathbf {X} _{y}^{\prime }\right) \le w\left( \mathbf {X}_{y}\right)$ by the Monge property.

Fig. 8

Transformation of block $\mathbf {X}_{y}$ into $\mathbf {X}_{y}^{\prime }$

In the case of $x_{j_{1}j_{1}}=x_{j_{2}j_{2}}=0, x_{j_{3}j_{3}}=1$, at least one of the values, a or t, is larger than 3 ($a=3$ or $t=3$ is not possible for $x_{j_{3}j_{3}}=1; a\le 2$ and $t\le 2$ is not possible since block $\mathbf {X}_{y}$ is large). If $t>3$, then the transformation is similar to that in Fig. 8: it involves 4 entries in rows $\left\{ j_{1},j_{3}\right\}$ and columns $\left\{ j_{3},j_{t}\right\}$. Alternatively, if $a>3$, then the transformation involves 4 entries in rows $\left\{ j_{3},j_{a}\right\}$ and columns $\left\{ j_{1},j_{3}\right\}$. In either case, the 1-entries in the initial solution belong to a diagonal of type $\diagup$ and to a diagonal of type $\diagdown$ after the transformation, so that the cost does not increase by the Monge property.

Thus, in the following we assume that condition (15) holds.

, or equivalently $x_{j_{1}j_{2}}=1$. This implies $b=1$. If $a\ne u$, then the transformation from $\mathbf {X}_{y}$ to $\bar{\mathbf {X}}_{y}$ shown in Fig. 9 creates a small block of size 2 without increasing the cost.

Fig. 9

Transformation of block $\mathbf {X}_{y}$ into $\bar{\mathbf {X}}_{y}$

Fig. 10

Cases where $t=2$ and $a=u \le 3$: (a) $a=u=1$, (b) $a=u=2$, (c) $a=u=3$

Consider the case $a=u$ and notice that we can assume $a=u>3$. Indeed, cases $a=u=1$ and $a=u=2$ cannot happen as the corresponding assignment is infeasible (see Fig. 10a, b), and in case $a=u=3$ the block is already small (see Fig. 10c). For $a=u>3$ the transformation illustrated in Fig. 9 is not applicable as it results in a new diagonal entry $x_{j_{a}j_{a}}=1$. Instead, we perform the two transformations from $\mathbf {X}_{y}$ to $\widetilde{\mathbf {X}}_{y}$ and then to $\widetilde{\widetilde{\mathbf {X}}}_{y}$ shown in Figs. 11 and 12, creating eventually a small block of size 3.

Fig. 11

Transformation from $\mathbf {X}_{y}$ to $\widetilde{\mathbf {X}}_{y}$

Fig. 12

Transformation from $\widetilde{\mathbf {X}}_{y}$ to $\widetilde{\widetilde{\mathbf {X}}}_{y}$

Observe that both of the values, c and v, are different from $a=u$. Note further that we have $c \ne 1$ as $t=2$, $c \ne 2$ as $u>3$, and $c \ne 3$ due to (15). Similarly $v \ne 1$ as $a>3$, $v \ne 2$ as $t=2$, and $v \ne 3$ due to (15). Thus $c>3$ and $v>3$. The relationship between $a=u$ and c is immaterial, as the above transformations work in both cases, $a=u<c$ and $a=u>c$. Similarly, the relationship between $a=u$ and v is immaterial as well. Moreover, the presented transformation works for either case, $c=v$ or $c\ne v$.

is similar to the case of $t=2$ since the ${{\mathbf {X}}}$-matrices for these two cases are transposes of each other. Recall that whenever the swaps are done in the case of $t=2$, the 1-entries on a diagonal of type $\diagup$ become 0-entries, while the 0-entries on a diagonal of type $\diagdown$ become 1-entries, so that the Monge inequality (3) is applicable. In the case of $a=2$, the initial 1-entries in the transpose matrix also belong to a diagonal of type $\diagup$, while the new 1-entries are created on a diagonal of type $\diagdown$.

. Consider the transformation from $\mathbf {X}_{y}$ to $\widehat{\mathbf {X}}_{y}$ shown in Fig. 13. It uses the Monge property two times, once for the entries in rows $\left\{ j_{2},j_{a}\right\}$ and columns $\left\{ j_{1},j_{u}\right\}$, and another time for the entries in rows $\left\{ j_{1},j_{b}\right\}$ and columns $\left\{ j_{2},j_{t}\right\}$.

Fig. 13

Transformation from $\mathbf {X}_{y}$ to $\widehat{\mathbf {X}}_{y}$

If $a\ne u$ and $b\ne t$, then the resulting matrix $\widehat{\mathbf {X}} _{y}$ satisfies the conditions of the lemma and a matrix without changed diagonal entries and with a small block of size 2 is obtained.

Consider the case $a=u$ or $b=t$. By the definition of the indices a, b, t, u, according to (13)–(14), we have $a\ne b$ and $t\ne u$. The latter two conditions, combined with either $a=u$ or $b=t$, imply $a \ne t$ and $b \ne u$.

Then, after $\mathbf {X}_{y}$ is transformed into $\widehat{\mathbf {X}}_{y}$, we perform one more transformation from $\widehat{\mathbf {X}}_{y}$ to $\widehat{\widehat{\mathbf {X}}}_{y}$ shown in Fig. 14. Then, the resulting matrix $\widehat{\widehat{\mathbf {X}}}_{y}$ satisfies the conditions of the lemma.

Fig. 14

Transformation from $\widehat{\mathbf {X}}_{y}$ to $\widehat{\widehat{\mathbf {X}}}_{y}$

. We start with an additional preprocessing step shown in Fig. 15 replacing $x_{1t}=x_{2u}=1$ by 0-entries and $x_{1u}=x_{2t}=0$ by 1-entries without increasing the cost.

Fig. 15

Transformation from $\mathbf {X}_{y}$ to $\mathbf {X}_{y}^{*}$

In the resulting matrix $\mathbf {X}_{y}^{*}$, we interchange the notation of the columns $j_{t}$ and $j_{u}$ in accordance with definition (14) and proceed as described above for the case $t<u$. Since $a>2$ and therefore $u \ne 1$, no new diagonal entry is produced in the preprocessing.

. This case corresponds to the transposed of the picture in the previous case. We undertake a similar preprocessing step as before, to transform this case into one with $a<b$. $\square$

Lemma 4

If a solution $\mathbf {X}$ contains an infeasible block of size 2, i.e., $x_{j_{1},j_{2}}=x_{j_{2},j_{1}}=1$ with at least one of the entries $(j_{1},j_{2})$ or $(j_{2},j_{1})$ belonging to ${{\mathcal {F}}}$, then without increasing the cost it can be replaced by two feasible blocks of size 1, given by $x_{j_{1},j_{1}}=1$ and $x_{j_{2},j_{2}}=1$.

Proof

For the above transformation the cost does not increase due to the Monge property. As far as feasibility is concerned, by the definition of set $\mathbf {\mathcal {F}}$, there is exactly one forbidden entry in each row and each column. Thus, if $(j_{1},j_{2})\in {{\mathcal {F}}}$, then neither $(j_{1},j_{1})$ nor $(j_{2},j_{2})$ are forbidden. Similar arguments hold for $(j_{2},j_{1})\in {{\mathcal {F}}}$. $\square$

Lemma 5

If a solution $\mathbf {X}$ contains an infeasible block of size 3, then that block can be replaced, without increasing the cost, by three feasible blocks of size 1, or by two feasible blocks, one of size 1 and another one of size 2.

Proof

Let $\mathbf {X}_{y}$ be an infeasible block consisting of rows and columns $j_{1}, j_{2}$ and $j_{3}$. The proof is presented for the case

$$\begin{aligned} x_{j_{1}j_{1}}=x_{j_{3}j_{3}}=0; \end{aligned}$$

otherwise $\mathbf {X}_{y}$ can be decomposed into smaller blocks. Under the above assumption, $\mathbf {X}_{y}$ is of one of the three types $\mathbf {X}_{y}^{(I)}, \mathbf {X}_{y}^{(II)}$ or $\mathbf {X}_{y}^{(III)}$, shown in Fig. 16.

Fig. 16

Blocks $\mathbf {X}_{y}^{(I)}, \mathbf {X}_{y}^{(II)}$ and $\mathbf {X}_{y}^{(III)}$

Notice that $\mathbf {X}_{y}^{(III)}$ can be replaced by $\mathbf {X} _{y}^{(II)}$ without increasing the cost, using the Monge property, and so we only have to deal with $\mathbf {X}_{y}^{(I)}$ and $\mathbf {X}_{y}^{(II)}$, which are symmetric. We first demonstrate that each block, $\mathbf {X}_{y}^{(I)}$ or $\mathbf {X}_{y}^{(II)}$, can be replaced by blocks $\mathbf {X}_{y}^{(a)}, \mathbf {X}_{y}^{(b)}$ or $\mathbf {X}_{y}^{(c)}$ shown in Fig. 17, without increasing the cost. Then we proof that at least one of those blocks is feasible.

Fig. 17

Blocks $\mathbf {X}_{y}^{(a)}, \mathbf {X}_{y}^{(b)}$ and $\mathbf {X}_{y}^{(c)}$

The transformation of $\mathbf {X} _{y}^{(I)}$ into $\mathbf {X}_{y}^{(a)}$ or $\mathbf {X}_{y}^{(b)}$ involves a quadruple of 1-entries, so that the cost does not increase due to the Monge property. Transforming $\mathbf {X}_{y}^{(I)}$ into the diagonal solution $\mathbf {X}_{y}^{(c)}$ we achieve a minimum cost assignment for the Monge submatrix given by rows and columns $\{ j_1, j_2, j_3 \}$ (see, e.g., Burkard et al. 1996). The same arguments hold for the transformation of $\mathbf {X}_{y}^{(II)}$ into $\mathbf {X}_{y}^{(a)}, \mathbf {X}_{y}^{(b)}$, or $\mathbf {X}_{y}^{(c)}$.

In the following, we deal with feasibility. If the initial infeasible block is of type $\mathbf {X}_{y}^{(I)}$, then at least one of the pairs $(j_{1},j_{3}), (j_{2},j_{1})$, or $(j_{3},j_{2})$ is forbidden. Therefore, at least one pair $(j_{1},j_{1})$ or $(j_{3},j_{3})$ is feasible. If $(j_{1},j_{1})$ is feasible, then block $\mathbf {X}_{y}^{(a)}$ or $\mathbf {X}_{y}^{(c)}$ is feasible. Similarly, if $(j_{3},j_{3})$ is feasible, then block $\mathbf {X}_{y}^{(b)}$ or $\mathbf {X}_{y}^{(c)}$ is feasible.

Similar arguments can be used if the initial infeasible block is of type $\mathbf {X}_{y}^{(II)}$. $\square$

Combining Lemmas 3–5 and using them repeatedly we arrive at the main result of Theorem 1. Below we present the formal proof.

Proof of Theorem 1: Consider any optimal solution. Apply Lemma 3 repeatedly until all blocks are of size 1, 2, or 3. Since all diagonal 1-entries of the new solution are also present in the original solution, those entries are feasible. Therefore, all blocks of size 1 are feasible. By Lemmas 4–5 all blocks of size 2 or 3 are either feasible or can be converted into feasible blocks without increasing the cost. Thus, the resulting solution has blocks of size 1, 2, and 3, it is feasible, and its cost is not larger than the cost of the original optimal solution.

Finally, the only small blocks that are not of type (6), have three 1’s on the secondary diagonal, since other configurations of 0’s and 1’s combine blocks of type (6). Due to the arguments used in the proof of Lemma 5 with respect to block $\mathbf {X}_{y}^{(III)}$, such blocks can also be eliminated, which concludes the proof.

Appendix 2: The proofs of the key statements from Section 4

We start Appendix 2 by summarizing the notions from graph theory required for Sect. 4. In an undirected graph $G=(V,E)$ we define a trail of length k as a sequence of vertices $(v_{0},v_{1},\ldots ,v_{k})$ with $\left\{ v_{i},v_{i+1}\right\} \in E$ for $i=0,\ldots ,k-1$. A path of length k is a trail of length k in which the vertices $v_{0},\ldots ,v_{k}$ are pairwise different. In a directed graph $\overrightarrow{G}=(V,\overrightarrow{E})$, a directed trail of length k is a sequence of vertices $(v_{0},v_{1},\ldots ,v_{k})$ with $(v_{i},v_{i+1})\in \overrightarrow{E}$ for $i=0,\ldots ,k-1$. A directed path is then defined similar to an undirected path. A Hamiltonian path (either directed or undirected) is a path of length |V| such that each $v\in V$ is contained in the path. An Eulerian trail (either directed or undirected) is a trail which uses every edge exactly once; it may use vertices multiple times if needed. An Eulerian tour is an Eulerian trail which starts and ends in the same vertex.

A graph $G=(V,E)$ is connected if for any two different vertices $v,w\in V$ there exists a path from v to w in G. A directed graph $\overrightarrow{G}=(V,\overrightarrow{E})$ is strongly connected if for each pair of different vertices $(v,w)\in V\times V$ there is a directed path from v to w in $\overrightarrow{G}.$

In a graph $G=(V,E)$ the number of edges incident with a vertex $v\in V$ is also called the degree of v, denoted by $\deg _{G}(v)$. For a directed graph $\overrightarrow{G}$, we distinguish between the out-degree $\deg _{ \overrightarrow{G}}^{+}(v)$ of a vertex v (the number of arcs leaving v) and the in-degree $\deg _{\overrightarrow{G}}^{-}(v)$ (the number of arcs entering v).

In Sect. 4 we are given a connected graph $G^{\prime }=(V^{\prime },E^{\prime })$ with $V^{\prime }=\{1,2,\ldots ,n-1\}$. To construct the graph $\overrightarrow{G}$ for problem AUX, we first construct the graph $G=(V,E)$ by adding a universal vertex 0 which is connected by an edge with every vertex. In a second step, we construct a directed graph $\overrightarrow{G}=(V,\overrightarrow{E})$ by replacing each edge $\{v,w\}\in E$ by two directed edges (v, w) and (w, v), one in each direction. Note that in $\overrightarrow{G}$ we have $\deg _{\overrightarrow{G}}^{-}(v)=\deg _{\overrightarrow{G} }^{+}(v)$ for all $v\in V$ by construction.

Lemma 6

The following statements are equivalent.

• (1) There exists a Hamiltonian path in $G'$.

• (2) There exists a Hamiltonian path in G ending in 0.

• (3) There exists a directed Hamiltonian path in $\overrightarrow{G}$ ending in 0.

• (4) There exists an Eulerian tour in $\overrightarrow{G}$, starting and ending in 0, such that the last n vertices form a Hamiltonian path.

Proof

The implications (1) $\Rightarrow$ (2) $\Rightarrow$ (3) are obvious. We prove that (3) $\Rightarrow$ (4). Suppose there exists a Hamiltonian path $h=(v_{0},v_{1},\ldots ,v_{n-1})$ in $\overrightarrow{G}$ with $v_{n-1}=0$. Then create a graph $\overrightarrow{G^{*}}$ by removing from $\overrightarrow{G}$ all arcs that appear in h. By the properties of vertex 0, graph $\overrightarrow{G^{*}}$ is still strongly connected. Furthermore, for each inner vertex $v_{1}, v_{2}, \ldots , v_{n-2}$ of h, its in-degree in $\overrightarrow{G^{*}}$ still equals its out-degree, as one entering and one leaving edge is removed for each of them. Lastly note that for $v_{n-1}=0$ we have $\deg _{\overrightarrow{G^{*}}}^{+}(0)=\deg _{\overrightarrow{G^{*}}}^{-}(0)+1$, as an arc entering 0 is removed, but not a leaving one. Similarly, for $v_{0}, \deg _{\overrightarrow{G^{*}}}^{-}(v_{0})= \deg _{\overrightarrow{G^{*}}}^{+}(v_{0})+1$, as an arc leaving $v_{0}$ is removed, but not the one entering $v_{0}$.

We conclude that $\overrightarrow{G^{*}}$ contains an Eulerian trail $\epsilon ^{*}$, that starts in 0 and ends in $v_{0}$. Then the concatenation $\epsilon =\epsilon ^{*}\circ h$ starts and ends in 0 and its last n vertices form a Hamiltonian path h.

It remains to prove (4) $\Rightarrow$ (1). Let $\epsilon$ be an Eulerian tour in $\overrightarrow{G}$, starting and ending in 0, such that the last n vertices form a Hamiltonian path, and let that path be $h=(v_{0},v_{1},...,v_{n-1})$ with $v_{n-1}=0$. Notice that the vertex 0 appears only once in h. Then $h^{*}=(v_{0},v_{1},...,v_{n-2})$ is a path in G. Since $h^{*}$ consists of all $n-1$ vertices of $G, h^{*}$ is a Hamiltonian path in $G'$. $\square$

The remainder of the appendix deals with Properties 1–8 from the proof of Theorem 6. These properties characterize the structure of an optimal schedule S for instance SO, under the assumption that $\sum C_{j}\le \varTheta$ for that schedule.

Lemma 7

An optimal schedule S for instance SO with $\sum C_{j}\le \varTheta$ satisfies Properties 1–8.

Proof

In each cycle in S, both operations are either short or long.

Assume the opposite and let s be the first cycle that contains a short and a long operation. Since the number of long operations is even, there is at least one further cycle t which contains operations of both types and in which the long operation is on a different machine than in cycle s. In the following, assume that long operations are on machine $M_{2}$ in cycle s and on machine $M_{1}$ in cycle t; the alternative case is similar. Let $J_{s}$ and $j_{s}$ be the jobs in cycle s, with the operation of $J_{s}$ being long and the operation of $j_{s}$ being short. Let $J_{t}$ and $j_{t}$ be the jobs in cycle t, with the operation of $J_{t}$ being long and the operation of $j_{t}$ being short.

Fig. 18

Creating a cycle of long operations and a cycle of short operations if $J_{s}\ne J_{t}$ and $j_{s}\ne j_{t}$

Assume first that $J_{s}\ne J_{t}$ and $j_{s}\ne j_{t}$. Construct a new schedule $S^{\prime }$ by swapping the operations on $M_{2}$, see Fig. 18. Then, the length of cycle s in $S^{\prime }$ decreases by at least $L-(\xi +K+1)$ while all other cycles keep their lengths unchanged. The completion time of job $J_{s}$ either decreases, if its second operation is in cycle after t, or it increases by at most $(\xi +K+1)$ plus the total length of cycles $s+1,\ldots ,t$. Thus, $C_{J_{s}}^{\prime }-C_{J_{s}}\le (t-s-1)L+(\xi +K+1)$. For all other jobs that finish in cycle s or later, the completion times decrease by at least $L-(\xi +K+1)$. As there are at least $t-s+1$ cycles in the tail part of the schedule, starting from cycle s, this affects at least $t-s+1$ jobs. Thus, the difference in total completion time is

$$\begin{aligned} \sum _{j\in N}(C_{j}^{\prime }-C_{j})\le & {} (t-s-1)L+(\xi +K+1)\\&+\sum _{j\in N\backslash \{J_{s}\}}(C_{j}^{\prime }-C_{j}) \\\le & {} (t-s-1)L+(\xi +K+1) \\&-(t-s+1)(L-(\xi +K+1)) \\< & {} -2L+|N|(\xi +K+1), \end{aligned}$$

where |N| is the the number of jobs in the instance SO or equivalently the number of cycles. To show that we get an improved solution $S^{\prime }$, we prove that

$$\begin{aligned} -2L+|N|(\xi +K+1)<0 \end{aligned}$$

(16)

using the estimate on $\sigma =|\overrightarrow{E}|/2$,

$$\begin{aligned} n\le \sigma < n^{2} \text { (for } n>2 \text {)}, \end{aligned}$$

(17)

combined with the definitions of $|N|, \xi , L$ and K:

$$\begin{aligned} K= & {} 8n, \end{aligned}$$

(18)

$$\begin{aligned} |N|= & {} 2n^{9}+4\sigma +2\le 2n^{9}+4n^{2}+2, \end{aligned}$$

(19)

$$\begin{aligned} \xi= & {} 4K\sigma ^{2}=32n\sigma ^{2}<32n^{5}, \end{aligned}$$

(20)

$$\begin{aligned} L= & {} 2n^{9}\xi =2n^{9}\cdot 32n\sigma ^{2}\ge 64n^{12}>576n^{10}\text { (for }n > 3\text {)}. \nonumber \\ \end{aligned}$$

(21)

Indeed,

$$\begin{aligned}&-2L+|N|(\xi +K+1)\le \\&\quad \le -2n^{9}\xi +2n^{9}(K+1)+(4\sigma +2)(\xi +K+1) \\&\quad<-576n^{10}+2n^{9}(8n+1) \\&\qquad +\,(4n^{2}+4)(32n^{5}+8n+1) \\&\quad<-576n^{10}+18n^{10}+8n^{2}\cdot 41n^{5}<0. \end{aligned}$$

Thus, swapping the operations leads to a smaller total completion time, contradicting that S has minimal total completion time.

Fig. 19

Creating a cycle of long operations and a cycle of short operations if $J_{s}=J_{t}, j_{s}\ne j_{t}$ and (a) there is a long operation in cycle $r, r<s$, (b) there is no long operation in any cycle $r, r<s$, but there is a long operation in cycle $u, u>s$

Consider the case $J_{s}=J_{t}, j_{s} \ne j_{t}$ and assume first that there are other long operations scheduled before s. The case where there is no other long operation scheduled prior to cycle s is discussed afterwards. Let r be the last cycle before s in which a long operation is scheduled, $r < s$. Since s is the first cycle that contains a short as well as a long operation, both operations in cycle r are long. In this case construct $S^{\prime }$ by exchanging in cycles r, s, and t the three operations on machine $M_{2}$ , as shown in Fig. 19a. As a result, the completion time of job $J_{r}$ either decreases, if the last operation of that job is in a cycle after cycle t, or it increases by at most $(s-r)(\xi +K+1)+(t-s) L$, where the first term represents the estimate on the length of short cycles $r+1,\ldots ,s$ in $S^{\prime }$ and the second term estimates the length of cycles $s+1,\ldots ,t$, which may be short or long. For all other jobs, including job $J_{s}$, that finish in cycle s or later, their completion times decrease by at least $L-(\xi +K+1)$. Note that there are at least $t-s+2$ such jobs. Thus,

$$\begin{aligned} \sum _{j\in N}(C_{j}^{\prime }-C_{j})\le & {} [(s-r)(\xi +K+1)+(t-s) L] \\&-(t-s+2)( L-(\xi +K+1)) \\= & {} -2L+(t-r+2)(\xi +K+1) < 0, \end{aligned}$$

where the last inequality can be proved as a slight modification of (16).

Assume now that there is no long operation scheduled prior to cycle s and let $u>s$ be the first cycle that contains a long operation of some job $J_{u}$ on the same machine as the long operation in cycle t. Construct $S^{\prime }$ by swapping the $M_{1}$-operations in cycles t and u and the $M_{2}$-operations in cycles s and t, see Fig. 19b for an example with $u>t$. The completion time of job $J_{s}$ (or job $J_{u}$ if $s<u<t$) increases by at most $|u-t|L$. For the remaining jobs scheduled in the tail part of the schedule, starting from cycle s, their completion times reduce by at least $L-(\xi +K+1)$. Again, using the evaluation from above, this leads to a decrease in the total completion time,

$$\begin{aligned} \sum _{j\in N}(C_{j}^{\prime }-C_{j})\le & {} |u-t|L-\left( \max \left\{ u,t\right\} -s+1\right) \\&\times \left( L-(\xi +K+1)\right) \\= & {} -\left( \min \left\{ u,t\right\} -s+1\right) L \\&+\left( \max \left\{ u,t\right\} -s+1\right) (\xi +K+1) \\\le & {} -2L+\left| N\right| (\xi +K+1)\overset{(16)}{<}0. \end{aligned}$$

In all previous cases a better schedule $S^{\prime }$ is constructed by grouping two short operations $j_{s}$ and $j_{t}$ in one cycle. Next, consider $j_{s}=j_{t}$ and first assume that there are other short operations scheduled in some cycle $r<s$. Since s is the first cycle that contains a short as well as a long operation, both operations in cycle r are short. Construct a schedule $S^{\prime }$ as illustrated in Fig. 20a. Then, the completion time of job $j_{s}$ decreases by at least $2(L-(\xi +K+1))$, as both its operations were paired with long operations before and are now paired with short ones. Further, the completion times of all jobs that were completed in cycles $r, r+1$, ..., $t-1$ in S, increase by at most $(\xi +K+1)$ and the completion times of all jobs that are completed in cycle t or later decrease by at least $L-(\xi +K+1)$. Thus,

$$\begin{aligned} \sum _{j\in N}(C_{j}^{\prime }-C_{j})\le & {} -2(L-(\xi +K+1))\\&+\,(t-r)(\xi +K+1)\\&-\,\left( L-(\xi +K+1)\right) \\<&-3L+(t-r+3)(\xi +K+1) < 0, \end{aligned}$$

where the last inequality can be proved similar to (16).

Consider now the case where $r>s$ and assume additionally that both operations in cycle r are short (see Fig. 20(b) for an example of $r>t>s$). In this case, the completion times of job $j_{s}$ and all jobs that finish in cycle s or later, except for job $J_{s}$, decrease by at least $L-2(\xi +K+1)$. The completion time of job $j_{s}$ decreases further by the total length $\varDelta$ of cycles $s+1$, ..., $t-1,$ while the completion time of job $J_{s}$ may increase by at most $2(\xi +K+1)$ plus $\varDelta$, again leading to a decrease in the total completion time:

$$\begin{aligned}&\sum _{j\in N}(C_{j}^{\prime }-C_{j}) \\&\quad \le -((\max \{t,r\}-s)\cdot (L-2(\xi +K+1))-\varDelta \\&\qquad +2(\xi +K+1)+\varDelta \\&\quad \le -2(L-2(\xi +K+1))+2(\xi +K+1) \\&\quad =-2L+6(\xi +K+1)\overset{(16)}{<}0, \end{aligned}$$

where the last inequality follows from (16) since $6<|N|=2n^{9}+4\sigma +2$.

Fig. 20

Creating a cycle of long operations and a cycle of short operations if $J_{s}\ne J_{t}, j_{s}=j_{t}$ and there is a cycle r with two short operations, (a) $r<s$, (b) $r>s$

The only remaining case with $j_{s}=j_{t}$ is where no cycle r exists such that both operations in r are short, i.e., all short operations are paired with long operations. In this case, for cycle s with a short operation on $M_1$ and a long operation on $M_2$, we select a cycle $t'$ similar to t, with a short operation on $M_2$ and a long operation on $M_1, t^{\prime } \ne t$ (such a cycle always exists for $n>2$). Then the two short operations in cycles s and $t^{\prime }$ belong to different jobs, and the case reduces to one of the cases with $j_s \ne j_t$ considered before.

In case that $j_{s}=j_{t}$ and $J_{s}=J_{t}$ we can first swap one of the long operations with a long operation in another cycle, as described for $J_{s}=J_{t}$, and afterwards continue with moving the two short operations to the front of the schedule, as described for $j_{s}=j_{t}$, again leading to a decrease in the total completion time. Therefore, in an optimal schedule there is no cycle consisting of a long and a short operation.

Property 1 is proved. From now on we refer to cycles as short or long assuming that there are no “mixed cycles” in an optimal schedule.

All long operations are scheduled in the last $2n^{9}+1$ cycles. This defines the splitting of schedule S into Parts 1 and 2, with cycles $1,2,\ldots ,4\sigma +1$ and $4\sigma +2,\ldots ,4\sigma +2+2n^{9}$.

Let $U=(s+1,\ldots ,t)$ be the last sequence of short cycles and let s be a long cycle that precedes U. Assume first that $\left| U\right| \ge 2$. Then, as cycles in U are the last short cycles, at least $|U|-1$ jobs finish within U (U may contain the two short operations of jobs $\text {Ve}_{0}^{d(0)}$ and $F_{0}$ for which their respective second, long operations may be scheduled in later cycles). Construct a schedule $S^{\prime }$ by moving the long cycle s after U, see Fig. 21. Then the completion times of at least $|U|-1$ jobs decrease by L while the completion times of the two jobs scheduled in cycle s in S increase by at most $\left| U\right| (\xi +K+1)$,

$$\begin{aligned} \sum _{j\in N}(C_{j}^{\prime }-C_{j})\le & {} -\left( \left| U\right| -1\right) L+2\left| U\right| (\xi +K+1) \\= & {} L-\left| U\right| \left( L-2(\xi +K+1)\right) . \end{aligned}$$

Using conditions $|U|\ge 2$ and $L-2(\xi +K+1)>0$ (which can be proved in the same way as (16)) we deduce

$$\begin{aligned}&\sum _{j\in N}(C_{j}^{\prime }-C_{j})\le L-2\left( L-2(\xi +K+1)\right) \\&\quad =-L + 4(\xi +K+1). \end{aligned}$$

The last expression is negative, again by the same arguments as (16). Thus, we get a contradiction to the optimality of S.

Fig. 21

Moving long cycle s after a sequence of short cycles $U=\{s+1,\ldots ,t\}$

If $\left| U\right| =1$ and the short cycle in U is different from

(22)

then at least one job, different from $\hbox {Ve}_{0}^{d(0)}$ and $F_{0}$, finishes in U. In this case the previous transformation reduces the completion time of at least one job by L, while the completion times of the two jobs scheduled in cycle s in S increase by at most $(\xi +K+1)$,

$$\begin{aligned} \sum _{j\in N}(C_{j}^{\prime }-C_{j})\le -L+2(\xi +K+1) < 0, \end{aligned}$$

where the last inequality can be proved in the same way as (16).

Consider now the case with U consisting of only one short cycle of the form (22). Notice that such a cycle is avoided in the optimal solution presented in Fig. 6.

Let $\widetilde{U}$ be the last sequence of short cycles before U and assume first that $\widetilde{U}$ is preceded by some long cycles. Clearly $\widetilde{U}$ does not contain short operations of jobs $F_0$ and $\text {Ve}_{0}^{d(0)}$, as they appear in U. Since no other job consists of both, long and short operations, at least $| \widetilde{U} |$ short jobs finish within $\widetilde{U}$. Then the arguments presented in the beginning of the proof of Property 2 are applicable for the set of cycles $\widetilde{U}$ used instead of U.

Lastly, consider the remaining case with U consisting of only one short cycle of the form (22) and there are no other short cycles in the preceding part of the schedule that follow a long cycle. Then, the first $4\sigma$ cycles are short and the cycle (22) appears among the last $2(n^{9}+1)$ cycles. Using pairwise interchange arguments it is easy to make sure that in an optimal schedule, the latter cycles are of the form shown in Fig. 22, where without loss of generality jobs $F_{i}$, except for $F_{0}$, are renumbered in the order they appear in schedule S on machine $M_{1}$.

Fig. 22

A special short cycle appearing among the last $2(n^9+1)$ cycles

In Fig. 22, $\tau$ is the number of jobs from the set $\{ F_1, F_2, ..., F_{2n^9} \}$ completed before cycle (22), $1 \le \tau \le 2n^9$. Let $\varDelta$ be the total length of the first $4\sigma$ short cycles. If the length of cycle (22) was L, then the total completion time of all long jobs would be

$$\begin{aligned} 2(n^{9}+1)\varDelta +2L\sum _{i=1}^{n^{9}+1}2i=2(n^{9}+1)\left( \varDelta +(n^{9}+2)L\right) . \end{aligned}$$

In reality, the length of cycle (22) is less than L by the amount $L-\left( \xi +K+1\right)$, so that completion times of the jobs that appear after $F_{\tau - 1}$, $F_{\tau }$ should be adjusted. The number of jobs completed in the corresponding tail part of the schedule is $2(n^9+1) - \tau$, so that

$$\begin{aligned} \sum _{\text {long jobs}}C_{j}= & {} 2(n^{9}+1)\left( \varDelta +(n^{9}+2)L\right) \\&-\,(2(n^{9}+1)-\tau )(L-\xi -K-1) \\= & {} 2(n^{9}+1)\left( (n^{9}+1)L+\varDelta +\xi +K+1\right) \\&+\,\tau (L-\xi -K-1). \end{aligned}$$

We demonstrate that the objective value for schedule S exceeds the given threshold $\varTheta$, using the estimate (17) together with the following conditions:

$$\begin{aligned} \begin{array}{l} \varDelta \ge 4\sigma \xi +2\sigma K, \\ L-\xi -K-1>0, \end{array} \end{aligned}$$

where the first one is a lower bound on $\varDelta$ calculated as the sum of processing times on the second machine of the short operations in the first $4\sigma$ cycles (which includes every operation except the zero-length operation of job $F_{0}$), while the second one can be proved in a similar way as (16). We have

$$\begin{aligned}&\sum \limits _{\text {long jobs}}C_{j}>\\&\quad 2(n^{9}+1) \left( (n^{9}+1)L+\left( 4\sigma \xi +2\sigma K\right) +\xi +K+1\right) . \end{aligned}$$

Recall that

$$\begin{aligned} \varTheta _{1}< & {} (8\sigma ^{2}+2\sigma )\xi +4\sigma ^{2}K+n^{2}, \\ \varTheta _{2}= & {} 2(n^{9}+1)\left( \left( n^{9}+1\right) L+4\sigma \xi +2\sigma K+n\right) , \end{aligned}$$

Thus,

$$\begin{aligned} \begin{array}{l} \sum \limits _{j\in N}C_{j}-\varTheta>\sum \limits _{\text {long jobs}}C_{j}-\varTheta _{1}-\varTheta _{2} \\ \quad>2n^{9}\left( \xi +K+1-n\right) -\left[ (8\sigma ^{2}+2\sigma )\xi +4\sigma ^{2}K+n^{2}\right] \\ \quad>2n^{9}\left( \xi +K+1-n\right) -\left[ 10n^{4}\xi +4n^{4}K+n^{4}\right] >0, \end{array} \end{aligned}$$

where the last inequality holds as $n\ge 2$. Thus, to achieve $\sum C_{j}\le \varTheta$ cycle (22) should not appear among the last $2{n}^{9}+1$ cycles. With the exchange arguments from above all other cycles containing short operations have to be scheduled prior to the long operations while the last $2{n}^{9}+1$ cycles only contain long operations.

The sum of completion times of all long jobs is at least $\varTheta _{2}$.

Due to Property 2, all long operations are scheduled in the last $2n^{9}+1$ cycles. Again by interchange arguments, the long cycle

should be the first one among all long cycles, while other long cycles should be grouped in pairs, as shown in Fig. 22. Following the arguments used in the proof of part “$\Rightarrow$ ” for calculating the sum of completion times of the long jobs, it is easy to verify that calculations (9)–(10) hold in the current case as well. Instead of the precise value of $\varDelta$ that leads to (11), now we can only substitute an estimate of $\varDelta$,

$$\begin{aligned} \varDelta \ge 4\sigma \xi +2\sigma K+n, \end{aligned}$$

which corresponds to the total length of short operations on machine $M_{1}$ . Thus, we obtain:

$$\begin{aligned}&\sum \limits _{\text {long jobs}}C_{j}\overset{(10)}{=}2\varDelta (n^{9}+1)+2\left( n^{9}+1\right) ^{2}L \nonumber \\&\quad \ge 2\left( 4\sigma \xi +2\sigma K+n\right) (n^{9}+1)+2\left( n^{9}+1\right) ^{2}L=\varTheta _{2}.\nonumber \\ \end{aligned}$$

(23)

In S, machine $M_{1}$ operates without idle times.

If there is an idle time on machine $M_{1}$, then $\varDelta \ge 4\sigma \xi +2\sigma K+n+1$ in Property 3 and thus

$$\begin{aligned}&\sum \limits _{j\in N}C_{j}>\sum \limits _{\text {long jobs}}C_{j}\overset{(23)}{=}2\varDelta (n^{9}+1)+2\left( n^{9}+1\right) ^{2}L \\&\quad>2\left( 4\sigma \xi +2\sigma K+n+1\right) (n^{9}+1)+2\left( n^{9}+1\right) ^{2}L \\&\quad = \varTheta _{2}+2(n^{9}+1) >\varTheta _{2}+\varTheta _{1}=\varTheta . \end{aligned}$$

Therefore, there should be no idle time on machine $M_{1}$ to achieve $\sum _{j \in N} C_j \le \varTheta$.

In Part 1 of S, job $\hbox {Ve} _{0}^{0}$ is processed in the first two cycles which are of the form

, where

represents a short operation. While the order of these two cycles is immaterial, without loss of generality we assume that

precedes

; otherwise the cycles can be swapped without changing the value of $\sum C_{j}$.

Since the sum of completion times of all long jobs is at least $\varTheta _{2}$ , the remaining $4\sigma$ short jobs may only contribute a total completion time of at most $\varTheta _{1}$ to obtain a schedule with total completion time $\sum C_{j}\le \varTheta$. For all of these jobs, their operations on machine $M_{2}$ have length of at least $\xi$. Thus, it is not possible for $i+1$ short jobs to be completed at time $i\xi$ and we can use the lower bound $i\xi$ for the completion time $C_{[i]}$ of the i-th job:

$$\begin{aligned} C_{[i]}\ge i\xi \quad \text {for }1\le i\le 4\sigma . \end{aligned}$$

(24)

This implies that

$$\begin{aligned} \sum \limits _{\text {short jobs}}C_{j}\ge \xi \sum _{i=1}^{4\sigma }i=2\sigma (4\sigma +1)\xi . \end{aligned}$$

Notice that for $i=1$ there is only one job that can be completed at time $\xi$, namely $\hbox {Ve} _{0}^{0}$, and this happens only if the first two cycles satisfy the statement of Property 5.

Suppose the statement of Property 5 does not hold for S. Then the above estimate needs to be adjusted by $\xi$ since in that case the completion time of the first completed job is at least $2\xi$ rather than $\xi$. It follows that

$$\begin{aligned}&\sum \limits _{\text {short jobs}}C_{j}-\varTheta _{1} \ge \left[ 2\sigma (4\sigma +1)\xi +\xi \right] \\&\qquad -\left[ (8\sigma ^{2}+2\sigma )\xi +4\sigma ^{2}K-2\sum \nolimits _{v\in V}vd(v)+n^{2}\right] \\&\quad =\xi -4\sigma ^{2}K+2\sum \nolimits _{v\in V}vd(v)-n^{2} \\&\quad =2\sum \nolimits _{v\in V}vd(v)-n^{2}. \end{aligned}$$

Notice that $n>2$ and by construction $d(v) \ge 2$ for each vertex v ($G^{\prime }$ is connected). This leads to $2\sum _{v\in V}vd(v) - n^2 \ge 2n(n-1) - n^2 = n^2 - 2n >0$ for $n>2$. Thus, the total completion time of all jobs is greater than $\varTheta$, a contradiction.

The two operations of each vertex-job and the two operations of each arc-job are processed in two consecutive cycles, first on $M_{1}$ and then on $M_{2}$.

We have demonstrated in the proof of Property 5 that $C_{[1]}<2\xi$ (with job $\hbox {Ve}_{0}^{0}$ defining $C_{[1]}$); otherwise the lower bound $\varTheta _{1}$ is violated. Similar arguments can be used to prove (by induction) that the lower bound $\varTheta _{1}$ is achievable only if $C_{[i]}<\left( i+1\right) \xi$ for $1\le i\le 4\sigma$. Combining this with (24) we can limit our consideration to schedules satisfying

$$\begin{aligned} i\xi \le C_{[i]}<\left( i+1\right) \xi \quad \text {for}\quad 1\le i\le 4\sigma . \end{aligned}$$

(25)

Property 6 holds for the first job $\hbox {Ve}_{0}^{0}$ due to Property 5. Let job j be the short job that is processed on machine $M_1$ in cycle 2. Then, as $\xi \le p_{1j} < 2 \xi$, for $\hbox {Ve}_0^0$ (25) is satisfied.

Suppose j does not satisfy the conditions of Property 6. Then cycle 3 consists of two short jobs k and $\ell$ that have not been processed yet in the preceding cycles. The situation is illustrated below.

In that case no job other than $\hbox {Ve}_0^0$ can be finished in the first three cycles, so $C_{[2]}$, corresponding to some job finishing no earlier than cycle 4, is at least as big as the finishing time of cycle 4. As the processing time of any short operation other than $\hbox {Ve}_0^0$ is at least $\xi$, cycles 2, 3, and 4 have a combined length of at least $3\xi$ as illustrated above. Thus, we have $C_{[2]} \ge 3\xi$ in violation of (25).

Therefore j should be processed in cycles 2 and 3, first on $M_{1}$ and then on $M_{2}$. The proof of Property 6 can be done by induction using the above arguments.

In Part 1 of S, machine $M_{1}$ alternates between processing arc-jobs and vertex-jobs. Moreover, an operation of a vertex-job corresponding to v is followed by an operation of an arc-job corresponding to an arc leaving v. Similarly, an operation of an arc-job for arc (v, w) is followed by an operation of a vertex-job for vertex w. By Property 6, the same is true for machine $M_{2}$ in Part 1 and in the first cycle that follows it.

Note that due to the numbers and distributions of vertex- and arc-jobs, if two vertex-jobs are scheduled consecutively, then there should also be two arc-jobs scheduled consecutively. Hence we can restrict our proof to the latter case. So assume there are cycles $s,s+1,s+2$ in which two operations of arc-jobs are scheduled consecutively on the first machine in cycles $s,s+1$ (and thus their second operations are scheduled in cycles $s+1,s+2$ by Property 6). Then, because the processing times of the arc-jobs are chosen such that they are no larger than $\xi +2n$ on machine $M_{1}$ and no smaller than $\xi +6n$ on machine $M_{2}$, there is an idle time on machine $M_{1}$ in cycle $s+1$, as illustrated below. However, this is a contradiction to Property 4 as Machine $M_{1}$ has to operate without idle time. Therefore this situation cannot happen, which proves the first part of Property 7.

We now show that an operation of a vertex-job corresponding to v is followed by an operation of an arc-job corresponding to an arc leaving v. Note that due to Property 6 a vertex- or arc-job processed on machine $M_{1}$ in some cycle s is processed on machine $M_{2}$ in cycle $s+1$. Assume there is an operation of vertex-job $\text {Ve}_{i}$ that is succeeded by an operation of an arc-job $\text {Ar}_{jk}$ for some $i\ne j$ in cycles $s,s+1$ on machine $M_{1}$ and $s+1,s+2$ on machine $M_{2}$.

Among all such pairs $\left( \text {Ve}_{i},\text {Ar}_{jk}\right)$ select the one with $i>j$ (notice that the case that $i<j$ for all pairs is not possible). Then there is an idle time on machine $M_{1}$ in cycle $s+1$, contradicting Property 4.

In a similar fashion it can be shown that an operation of an arc-job corresponding to an arc entering a vertex w is followed by a vertex-job corresponding to vertex w.

The first arc-job that appears in S corresponds to an arc leaving 0 . Among the vertex-jobs, the last one is $\text {Ve}_{0}^{d(0)}$.

Due to Property 5, the first two cycles contain the two operations of job $\text {Ve}_0^0$. Thus, according to Property 7, both operations of this job have to be succeeded by operations of an arc-job leaving vertex 0. Further, as shown in the proof of Property 6, the last vertex-job to be completed is $\text {Ve}_{0}^{d(0)}$.$\square$