Skip to main content
SpringerLink
Log in

A Third Order Fast Sweeping Method with Linear Computational Complexity for Eikonal Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

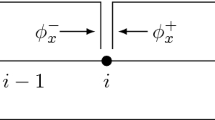
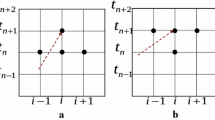
Abstract

Fast sweeping methods are a class of efficient iterative methods for solving steady state hyperbolic PDEs. They utilize the Gauss-Seidel iterations and alternating sweeping strategy to cover a family of characteristics of the hyperbolic PDEs in a certain direction simultaneously in each sweeping order. The first order fast sweeping method for solving Eikonal equations (Zhao in Math Comput 74:603–627, 2005) has linear computational complexity, namely, the computational cost is \(O(N)\) where \(N\) is the number of grid points of the computational mesh. Recently, a second order fast sweeping method with linear computational complexity was developed in Zhang et al. (SIAM J Sci Comput 33:1873–1896, 2011). The method is based on a discontinuous Galerkin (DG) finite element solver and causality indicators which guide the information flow directions of the nonlinear Eikonal equations. How to extend the method to higher order accuracy is still an open problem, due to the difficulties of solving much more complicated local nonlinear systems and calculations of local causality information. In this paper, we extend previous work and develop a third order fast sweeping method with linear computational complexity for solving Eikonal equations. A novel approach is designed for capturing the causality information in the third order DG local solver. Numerical experiments show that the method has third order accuracy and a linear computational complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Boué, M., Dupuis, P.: Markov chain approximations for deterministic control problems with affine dynamics and quadratic cost in the control. SIAM J. Numer. Anal. 36, 667–695 (1999)

    Article  MathSciNet  Google Scholar 

  2. Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for directly solving the Hamilton–Jacobi equations. J. Comput. Phys. 223, 398–415 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  3. Crandall, M.G., Lions, P.L.: Viscosity solutions of Hamilton–Jacobi equations. Trans. Am. Math. Soc. 277, 1–42 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Dijkstra, E.W.: A note on two problems in connection with graphs. Numer. Math. 1, 269–271 (1959)

    Article  MathSciNet  MATH  Google Scholar 

  5. Fomel, S., Luo, S., Zhao, H.: Fast sweeping method for the factored eikonal equation. J. Comput. Phys. 228, 6440–6455 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Helmsen, J., Puckett, E., Colella, P., Dorr, M.: Two new methods for simulating photolithography development in 3D. Proc. SPIE 2726, 253–261 (1996)

    Article  Google Scholar 

  7. Hu, C., Shu, C.-W.: A discontinuous Galerkin finite element method for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 20, 666–690 (1999)

    Article  MathSciNet  Google Scholar 

  8. Huang, L., Shu, C.-W., Zhang, M.: Numerical boundary conditions for the fast sweeping high order WENO methods for solving the Eikonal equation. J. Comput. Math. 26, 336–346 (2008)

    MathSciNet  MATH  Google Scholar 

  9. Jiang, G.-S., Peng, D.: Weighted ENO schemes for Hamilton–Jacobi equations. SIAM J. Sci. Comput. 21, 2126–2143 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kao, C.Y., Osher, S., Qian, J.: Lax–Friedrichs sweeping schemes for static Hamilton–Jacobi equations. J. Comput. Phys. 196, 367–391 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  11. Kao, C.Y., Osher, S., Qian, J.: Legendre-transform-based fast sweeping methods for static Hamilton–Jacobi equations on triangulated meshes. J. Comput. Phys. 227, 10209–10225 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Li, F., Shu, C.-W., Zhang, Y.-T., Zhao, H.-K.: A second order discontinuous Galerkin fast sweeping method for Eikonal equations. J. Comput. Phys. 227, 8191–8208 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  13. Qian, J., Zhang, Y.-T., Zhao, H.-K.: Fast sweeping methods for Eikonal equations on triangular meshes. SIAM J. Numer. Anal. 45, 83–107 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Qian, J., Zhang, Y.-T., Zhao, H.-K.: A fast sweeping method for static convex Hamilton–Jacobi equations. J. Sci. Comput. 31, 237–271 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Rouy, E., Tourin, A.: A viscosity solutions approach to shape-from-shading. SIAM J. Numer. Anal. 29, 867–884 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  16. Serna, S., Qian, J.: A stopping criterion for higher-order sweeping schemes for static Hamilton–Jacobi equations. J. Comput. Math. 28, 552–568 (2010)

    MathSciNet  MATH  Google Scholar 

  17. Sethian, J.A.: A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA 93, 1591–1595 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  18. Sethian, J.A., Vladimirsky, A.: Ordered upwind methods for static Hamilton–Jacobi equations. Proc. Natl. Acad. Sci. USA 98, 11069–11074 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  19. Sethian, J.A., Vladimirsky, A.: Ordered upwind methods for static Hamilton–Jacobi equations: theory and algorithms. SIAM J. Numer. Anal. 41, 325–363 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  20. Tan, S., Shu, C.-W.: Inverse Lax-Wendroff procedure for numerical boundary conditions of conservation laws. J. Comput. Phys. 229, 8144–8166 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Tsai, Y.-H., Cheng, L.-T., Osher, S., Zhao, H.-K.: Fast sweeping algorithms for a class of Hamilton–Jacobi equations. SIAM J. Numer. Anal. 41, 673–694 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  22. Tsitsiklis, J.N.: Efficient algorithms for globally optimal trajectories. IEEE Trans. Autom. Control 40, 1528–1538 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  23. Xiong, T., Zhang, M., Zhang, Y.-T., Shu, C.-W.: Fifth order fast sweeping WENO scheme for static Hamilton–Jacobi equations with accurate boundary treatment. J. Sci. Comput. 45, 514–536 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhang, Y.-T., Chen, S., Li, F., Zhao, H., Shu, C.-W.: Uniformly accurate discontinuous Galerkin fast sweeping methods for Eikonal equations. SIAM J. Sci. Comput. 33, 1873–1896 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhang, Y.-T., Shu, C.-W.: High order WENO schemes for Hamilton–Jacobi equations on triangular meshes. SIAM J. Sci. Comput. 24, 1005–1030 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  26. Zhang, Y.-T., Zhao, H.-K., Chen, S.: Fixed-point iterative sweeping methods for static Hamilton–Jacobi equations. Methods Appl. Anal. 13, 299–320 (2006)

    MathSciNet  MATH  Google Scholar 

  27. Zhang, Y.-T., Zhao, H.-K., Qian, J.: High order fast sweeping methods for static Hamilton–Jacobi equations. J. Sci. Comput. 29, 25–56 (2006)

    Article  MathSciNet  Google Scholar 

  28. Zhao, H.-K.: A fast sweeping method for Eikonal equations. Math. Comput. 74, 603–627 (2005)

    Article  MATH  Google Scholar 

  29. Zhao, H., Osher, S., Merriman, B., Kang, M.: Implicit and non-parametric shape reconstruction from unorganized points using variational level set method. Comput. Vis. Image Underst. 80, 295–319 (2000)

    Article  MATH  Google Scholar 

Download references

Acknowledgments

We thank helpful discussions with Chi-Wang Shu and Hongkai Zhao on this project

Author information

Authors and Affiliations

  1. Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, IN, 46556, USA

    Liang Wu & Yong-Tao Zhang

Authors
  1. Liang Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong-Tao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong-Tao Zhang.

Appendix: Detailed Formulae of the \(6 \times 6\) Jacobian Matrix in Solving the Local Nonlinear System

Appendix: Detailed Formulae of the \(6 \times 6\) Jacobian Matrix in Solving the Local Nonlinear System

$$\begin{aligned} J(1,1)&= \frac{\partial f_1}{\partial \phi }=l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \\ J(1,2)&= \frac{\partial f_1}{\partial u}=8k~u_{ij}+l_j(-\alpha _l-\alpha _r) \\ J(1,3)&= \frac{\partial f_1}{\partial v}=\frac{8}{k}~v_{ij}+h_i(-\alpha _b-\alpha _t) \\ J(1,4)&= \frac{\partial f_1}{\partial a}=\frac{32k}{3}~a_{ij}+l_j(\alpha _l-\alpha _r)+\frac{1}{3}h_i(\alpha _b-\alpha _t) \\ J(1,5)&= \frac{\partial f_1}{\partial b}=\frac{32}{3k}~b_{ij}+\frac{1}{3}l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \\ J(1,6)&= \frac{\partial f_1}{\partial c}=(\frac{8k}{3}+\frac{8}{3k})~c_{ij} \end{aligned}$$
$$\begin{aligned} J(2,1)&= \frac{\partial f_2}{\partial \phi }=l_j(-\alpha _l-\alpha _r) \\ J(2,2)&= \frac{\partial f_2}{\partial u}=\frac{16k}{3}~a_{ij}+l_j(\alpha _l-\alpha _r)+\frac{1}{3}h_i(\alpha _b-\alpha _t) \\ J(2,3)&= \frac{\partial f_2}{\partial v}=\frac{8}{3k}~c_{ij} \\ J(2,4)&= \frac{\partial f_2}{\partial a}=\frac{16k}{3}~u_{ij}+l_j(-\alpha _l-\alpha _r) \\ J(2,5)&= \frac{\partial f_2}{\partial b}=\frac{1}{3}l_j(-\alpha _l-\alpha _r) \\ J(2,6)&= \frac{\partial f_2}{\partial c}=\frac{8}{3k}~v_{ij}+\frac{1}{3}h_i(-\alpha _b-\alpha _t) \end{aligned}$$
$$\begin{aligned} J(3,1)&= \frac{\partial f_3}{\partial \phi }=h_i(-\alpha _b-\alpha _t) \\ J(3,2)&= \frac{\partial f_3}{\partial u}=\frac{8k}{3}~c_{ij} \\ J(3,3)&= \frac{\partial f_3}{\partial v}=\frac{16}{3k}~b_{ij} + \frac{1}{3}l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \\ J(3,4)&= \frac{\partial f_3}{\partial a}=\frac{1}{3}h_i(-\alpha _b-\alpha _t) \\ J(3,5)&= \frac{\partial f_3}{\partial b}=\frac{16}{3k}v_{ij} + h_i(-\alpha _b-\alpha _t) \\ J(3,6)&= \frac{\partial f_3}{\partial c}=\frac{8k}{3}~u_{ij}+ \frac{1}{3}l_j(-\alpha _l-\alpha _r) \end{aligned}$$
$$\begin{aligned} J(4,1)&= \frac{\partial f_4}{\partial \phi }= l_j(\alpha _l-\alpha _r)+\frac{1}{3}h_i(\alpha _b-\alpha _t) \\ J(4,2)&= \frac{\partial f_4}{\partial u}=\frac{8k}{3}~u_{ij}+ l_j(-\alpha _l-\alpha _r) \\ J(4,3)&= \frac{\partial f_4}{\partial v}=\frac{8}{3k}~v_{ij}+\frac{1}{3}h_i(-\alpha _b-\alpha _t) \\ J(4,4)&= \frac{\partial f_4}{\partial a}=\frac{32k}{5}~a_{ij}+ l_j(\alpha _l-\alpha _r)+\frac{1}{5}h_i(\alpha _b-\alpha _t) \\ J(4,5)&= \frac{\partial f_4}{\partial b}= \frac{32}{9k}~b_{ij}+ \frac{1}{3}\big ( l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \big ) \\ J(4,6)&= \frac{\partial f_4}{\partial c}= (\frac{8k}{9}+\frac{8}{5k})~c_{ij} \end{aligned}$$
$$\begin{aligned} J(5,1)&= \frac{\partial f_5}{\partial \phi }=\frac{1}{3}l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \\ J(5,2)&= \frac{\partial f_5}{\partial u}=\frac{8k}{3}~u_{ij}+\frac{1}{3}l_j(-\alpha _l-\alpha _r) \\ J(5,3)&= \frac{\partial f_5}{\partial v}=\frac{8}{3k}~v_{ij}+h_i(-\alpha _b-\alpha _t) \\ J(5,4)&= \frac{\partial f_5}{\partial a}=\frac{32k}{9}~a_{ij}+\frac{1}{3}\big ( l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \big ) \\ J(5,5)&= \frac{\partial f_5}{\partial b}=\frac{32}{5k}~b_{ij}+ \frac{1}{5}l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \\ J(5,6)&= \frac{\partial f_5}{\partial c}= (\frac{8k}{5}+\frac{8}{9k})~c_{ij} \end{aligned}$$
$$\begin{aligned} J(6,1)&= \frac{\partial f_6}{\partial \phi }=0 \\ J(6,2)&= \frac{\partial f_6}{\partial u}=\frac{1}{3}h_i(-\alpha _b-\alpha _t) \\ J(6,3)&= \frac{\partial f_6}{\partial v}=\frac{1}{3}l_j(-\alpha _l-\alpha _r) \\ J(6,4)&= \frac{\partial f_6}{\partial a}=\frac{16k}{9}~c_{ij} \\ J(6,5)&= \frac{\partial f_6}{\partial b}=\frac{16}{9k}~c_{ij} \\ J(6,6)&= \frac{\partial f_6}{\partial c}=\frac{16k}{9}~a_{ij}+\frac{16}{9k}~b_{ij}+\frac{1}{3}\big ( l_j(\alpha _l-\alpha _r)+h_i(\alpha _b-\alpha _t) \big ) \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, L., Zhang, YT. A Third Order Fast Sweeping Method with Linear Computational Complexity for Eikonal Equations. J Sci Comput 62, 198–229 (2015). https://doi.org/10.1007/s10915-014-9856-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-014-9856-7

Keywords

Mathematics Subject Classification

Search

Navigation