Skip to main content
SpringerLink
Log in

Linear conjugacy in biochemical reaction networks with rational reaction rates

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

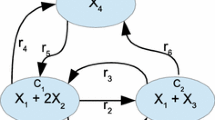
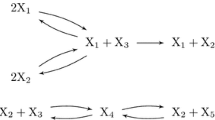
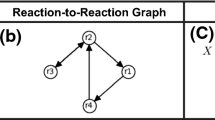
In this paper we show that the model form of a wide class of kinetic systems with rational terms in the reaction rates is invariant under a positive linear diagonal transformation. Thus, the concept of linear conjugacy defined originally for mass action systems is extended to rational biochemical models. The generalized Kirchhoff matrix and the kinetic weighting matrix of the linearly conjugate models are given as functions of the computed transformation parameters. It is shown through the illustrative examples that the dense realization of a linearly conjugate rational model may contain more reactions than that of a dynamically equivalent one due to the additional degrees of freedom introduced by the linear transformation. The proposed matrix-based representation is suitable for the computational search of preferred graph structures corresponding to linearly conjugate realizations of rational kinetic models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. B. Ács, G. Szederkényi, Z. Tuza, Z.A. Tuza, Computing linearly conjugate weakly reversible kinetic structures using optimization and graph theory. MATCH Commun. Math. Comput. Chem. 74(3), 481–504 (2015)

    Google Scholar 

  2. D.F. Anderson, A proof of the global attractor conjecture in the single linkage class case. SIAM J. Appl. Math. 71, 1487–1508 (2011)

    Article  CAS  Google Scholar 

  3. D. Angeli, P. De Leenher, E.D. Sontag, A Petri net approach to the study of persistence in chemical reaction networks. Math. Biosci. 210, 598–618 (2007)

    Article  CAS  Google Scholar 

  4. M. Banaji, C. Pantea, Some results on injectivity and multistationarity in chemical reaction networks. arXiv:1309.6771 [math.DS] (2015)

  5. V. Chellaboina, Modeling and analysis of mass-action kinetics. IEEE Control Syst. Mag. 29, 60–78 (2009)

    Article  Google Scholar 

  6. G. Craciun, Toric differential inclusions and a proof of the global attractor conjecture. arXiv:1501.02860v2 [math.DS] (2016)

  7. G. Craciun, C. Pantea, Identifiability of chemical reaction networks. J. Math. Chem. 44, 244–259 (2008)

    Article  CAS  Google Scholar 

  8. G. Craciun, M. Feinberg, Multiple equilibria in complex chemical reaction networks: I. The injectivity property. SIAM J. Appl. Math. 65(5), 1526–1546 (2005)

    Article  CAS  Google Scholar 

  9. A. Császár, L. Jicsinszky, T. Turányi, Generation of model reactions leading to limit cycle behaviour. React. Kinet. Catal. Lett 18(1–2), 65–71 (1981)

    Google Scholar 

  10. P. Donnell, M. Banaji, Local and global stability of equilibria for a class of chemical reaction networks. SIAM J. Appl. Dyn. Syst. 12, 899–920 (2013)

    Article  Google Scholar 

  11. P. Érdi, J. Tóth, Mathematical Models of Chemical Reactions. Theory and Applications of Deterministic and Stochastic Models (Manchester University Press, Princeton University Press, Manchester, Princeton, 1989)

    Google Scholar 

  12. G. Farkas, Kinetic lumping schemes. Chem. Eng. Sci. 54, 3909–3915 (1999)

    Article  CAS  Google Scholar 

  13. M. Feinberg, Chemical reaction network structure and the stability of complex isothermal reactors—I. The deficiency zero and deficiency one theorems. Chem. Eng. Sci. 42(10), 2229–2268 (1987)

    Article  CAS  Google Scholar 

  14. M. Feinberg, Necessary and sufficient conditions for detailed balancing mass action systems of arbitrary complexity. Chem. Eng. Sci. 44(9), 1819–1827 (1989)

    Article  CAS  Google Scholar 

  15. A. Gábor, K.M. Hangos, J.R. Banga, G. Szederkényi, Reaction network realizations of rational biochemical systems and their structural properties. J. Math. Chem. 53, 1657–1686 (2015)

    Article  Google Scholar 

  16. V. Hárs, J. Tóth, On the inverse problem of reaction kinetics, in Coll. Math. Soc. J. Bolyai, vol. 30, ed. by M. Farkas, L. Hatvani (North-Holland, Amsterdam, 1981), pp. 363–379

    Google Scholar 

  17. B. Hernandez-Bermejo, V. Fairen, L. Brenig, Algebraic recasting of nonlinear ODEs into universal formats. J. Phys. A Math. Gen. 31, 2415–2430 (1998)

    Article  Google Scholar 

  18. F. Horn, R. Jackson, General mass action kinetics. Arch. Ration. Mech. Anal. 47(2), 81–116 (1972)

    Article  Google Scholar 

  19. M.D. Johnston, D. Siegel, G. Szederkényi, A linear programming approach to weak reversibility and linear conjugacy of chemical reaction networks. J. Math. Chem. 50, 274–288 (2012)

    Article  CAS  Google Scholar 

  20. M.D. Johnston, D. Siegel, Linear conjugacy of chemical reaction networks. J. Math. Chem. 49(7(7)), 1263–1282 (2011)

    Article  CAS  Google Scholar 

  21. M.D. Johnston, D. Siegel, G. Szederkényi, Dynamical equivalence and linear conjugacy of chemical reaction networks: new results and methods. MATCH Commun. Math. Comput. Chem. 68, 443–468 (2012)

    CAS  Google Scholar 

  22. M.D. Johnston, D. Siegel, G. Szederkényi, Computing weakly reversible linearly conjugate chemical reaction networks with minimal deficiency. Math. Biosci. 241(1(1)), 88–98 (2013)

    Article  CAS  Google Scholar 

  23. G. Lipták, G. Szederkényi, K.M. Hangos, Computing zero deficiency realizations of kinetic systems. Syst. Control Lett. 81, 24–30 (2015)

    Article  Google Scholar 

  24. J. Löfberg. YALMIP : A Toolbox for Modeling and Optimization in MATLAB. in Proceedings of the CACSD Conference, Taipei, Taiwan (2004)

  25. M. Mincheva, D. Siegel, Stability of mass action reaction–diffusion systems. Nonlinear Anal. Theory Methods Appl. 56(8), 1105–1131 (2004)

    Article  Google Scholar 

  26. M. Mincheva, M.R. Roussel, Graph-theoretic methods for the analysis of chemical and biochemical networks. I. Multistability and oscillations in ordinary differential equation models. J. Math. Biol. 55(1), 61–86 (2007)

    Article  Google Scholar 

  27. S. Müller, G. Regensburger, Generalized mass action systems: complex balancing equilibria and sign vectors of the stoichiometric and kinetic-order subspaces. SIAM J. Appl. Math. 72, 1926–1947 (2012)

    Article  Google Scholar 

  28. J. Rudan, G. Szederkényi, K.M. Hangos, Efficient computation of alternative structures for large kinetic systems using linear programming. MATCH Commun. Math. Comput. Chem. 71, 71–92 (2014)

    CAS  Google Scholar 

  29. N. Samardzija, L.D. Greller, E. Wassermann, Nonlinear chemical kinetic schemes derived from mechanical and electrical dynamical systems. J. Chem. Phys. 90(4), 2296–2304 (1989)

    Article  CAS  Google Scholar 

  30. G. Shinar, M. Feinberg, Structural sources of robustness in biochemical reaction networks. Science 327(5971), 1389–1391 (2010)

    Article  CAS  Google Scholar 

  31. G. Szederkényi, Computing sparse and dense realizations of reaction kinetic systems. J. Math. Chem. 47(2), 551–568 (2010)

    Article  Google Scholar 

  32. G. Szederkényi, K.M. Hangos, Z.S. Tuza, Finding weakly reversible realizations of chemical reaction networks using optimization. MATCH Commun. Math. Comput. Chem. 67, 193–212 (2012)

    Google Scholar 

  33. L. Szili, J. Tóth, On the origin of Turing instability. J. Math. Chem. 22(1), 39–53 (1997)

    Article  CAS  Google Scholar 

  34. A.I. Vol’pert, Differential equations on graphs. Math. USSR-Sbornik 17(4), 571–582 (1972)

    Article  Google Scholar 

Download references

Acknowledgments

AG is supported by the funding from EU FP7 ITN “NICHE”, Project No. 289384. KMH acknowledges the funding from the National Research, Development and Innovation Office—NKFIH through Grant No. 115694. GSz acknowledges the support of the National Research, Development and Innovation Office—NKFIH through Grant No. NF104706. The authors thank Bernadett Ács for carefully reading the manuscript.

Author information

Authors and Affiliations

  1. BioProcess Engineering Group, IIM-CSIC, Spanish Council for Scientific Research, Eduardo Cabello 6, 36208, Vigo, Spain

    Attila Gábor

  2. Process Control Research Group, Institute for Computer Science and Control of the Hungarian Academy of Sciences (MTA SZTAKI), Kende u. 13-17, 1111, Budapest, Hungary

    Katalin M. Hangos & Gábor Szederkényi

  3. Department of Electrical Engineering and Information Systems, University of Pannonia, Egyetem u. 10, 8200, Veszprém, Hungary

    Katalin M. Hangos

  4. Faculty of Information Technology and Bionics, Pázmány Péter Catholic University, Práter u. 50/a, 1083, Budapest, Hungary

    Gábor Szederkényi

Authors
  1. Attila Gábor
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Katalin M. Hangos
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gábor Szederkényi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gábor Szederkényi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gábor, A., Hangos, K.M. & Szederkényi, G. Linear conjugacy in biochemical reaction networks with rational reaction rates. J Math Chem 54, 1658–1676 (2016). https://doi.org/10.1007/s10910-016-0642-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-016-0642-7

Keywords

Search

Navigation