Finite-Size Bath in Qubit Thermodynamics

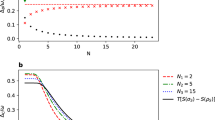
Abstract

We discuss a qubit weakly coupled to a finite-size heat bath (calorimeter) from the point of view of quantum thermodynamics. The energy deposited to this environment together with the state of the qubit provides a basis to analyze the heat and work statistics of this closed combined system. We present results on two representative models, where the bath is composed of two-level systems or harmonic oscillators, respectively. Finally, we derive results for an open quantum system composed of the above qubit plus finite-size bath, but now the latter is coupled to a practically infinite bath of the same nature of oscillators or two-level systems.

Appendix: Analytic Treatment of Fluctuation Relations

In what follows, we discuss the Crooks and Jarzynski equalities for trajectories up to a single jump. We assume that the qubit is driven resonantly in time $\tau$. In the absence of jumps, the amplitudes of the wavefunction $|\psi (\tau )\rangle = c(\tau )|g\rangle + d(\tau )|e\rangle$ evolve, up to the first order in $\Delta \Gamma = \Gamma _\downarrow - \Gamma _\uparrow$ as [29]

$$\begin{aligned} |c_g(\tau ,t_i;M_{\text {c}})|^2= & {} 1 - |d_g(\tau ,t_i;M_{\text {c}})|^2 \nonumber \\= & {} \cos ^2\frac{ F (\tau -t_i)}{2\hbar } + \frac{\hbar \Delta \Gamma (M_{\text {c}})}{F} \cos \frac{F (\tau -t_i)}{2\hbar } \sin ^3 \frac{F (\tau -t_i)}{2\hbar }, \end{aligned}$$

(26)

$$\begin{aligned} |c_e(\tau ,t_i;M_{\text {c}}|^2= & {} 1 - |d_e(\tau ,t_i;M_{\text {c}})|^2 \nonumber \\= & {} \sin ^2\frac{ F (\tau -t_i)}{2\hbar } + \frac{\hbar \Delta \Gamma (M_{\text {c}})}{F} \cos \frac{F (\tau -t_i)}{2\hbar } \sin ^3 \frac{F (\tau -t_i)}{2\hbar }, \qquad \quad \end{aligned}$$

(27)

where subscripts g and e refer to the evolution starting at $\tau =t_i$ in the ground or the excited state, respectively. As written explicitly, the rates $\Gamma _{\uparrow ,\downarrow }(M_{\text {c}})$ are to be understood as those corresponding to the instantaneous state of the calorimeter. It is useful to define

$$\begin{aligned} \Pi _{g,e}(t_2,t_1;M_{\text {c}}) = \int _{t_1}^{t_2} d\tau [\Gamma _\uparrow (M_{\text {c}}) |c_{g,e}(\tau ,t_1;M_{\text {c}})|^2 + \Gamma _\downarrow (M_{\text {c}}) |d_{g,e}(\tau ,t_1;M_{\text {c}})|^2],\nonumber \\ \end{aligned}$$

(28)

which yields the probabilities in the form $\mathrm{e}^{-\Pi _{g,e}(t_2,t_1;M_{\text {c}})}$ of not making a jump in the time interval $[t_1,t_2]$ starting in the ground or the excited state at $\tau =t_1$. Integrating Eq. (28) using Eqs. (27) and (26), we obtain

$$\begin{aligned} \Pi _{g,e}(\tau ,0;M_{\text {c}})= \frac{\Gamma _\Sigma (M_{\text {c}}) \tau }{2 }\mp \frac{\hbar \Delta \Gamma (M_{\text {c}})}{2 F} \sin \frac{F \tau }{\hbar }, \end{aligned}$$

(29)

again up to the linear order in $\Gamma$s. Here $\Gamma _{\Sigma }(M_{\text {c}})=\Gamma _{\downarrow }(M_{\text {c}})+\Gamma _{\uparrow }(M_{\text {c}})$. As an illustrative example, we choose in what follows the duration of the drive t to correspond to a $\pi$-pulse, by setting $F t/\hbar = \pi$.

1.1 Crooks and Jarzynski Relations

We will evaluate the following expressions up to the linear order in $\Gamma$s. In particular, we calculate the ratios $P_i(-W)/P_i(W)$, where W is the work in a realization and $i=0,1$ refers to the number of jumps in a trajectory.

The no-jump trajectories can yield work values $W=-\hbar \omega _0, 0, +\hbar \omega _0$ depending on the outcome of the first and second measurement. Therefore, in this case, we evaluate $P_0(-\hbar \omega _0)/P_0(+\hbar \omega _0)$. $W=+\hbar \omega _0$ for the process, where the first measurement finds the system in the ground state and the second one in the excited state, with the probability

$$\begin{aligned} P_0(+\hbar \omega _0)=\left\langle p_ge^{-\Pi _g(t,0;M_{\text {c}})}|d_g(t,0;M_{\text {c}})|^2 \right\rangle _{M_{\text {c}}}, \end{aligned}$$

(30)

and correspondingly

$$\begin{aligned} P_0(-\hbar \omega _0)=\left\langle p_ee^{-\Pi _e(t,0;M_{\text {c}})}|c_e(t,0;M_{\text {c}})|^2\right\rangle _{M_{\text {c}}}. \end{aligned}$$

(31)

For the $\pi$-pulse $\Pi _g(t,0;M_{\text {c}})=\Pi _e(t,0;M_{\text {c}})=\Gamma _\Sigma (M_{\text {c}})t/2$ and $|d_g(t,0;M_{\text {c}})|^2 = |c_e(t,0;M_{\text {c}})|^2 =1$, which yield

$$\begin{aligned} P_0(-\hbar \omega _0)/P_0(+\hbar \omega _0)=p_e/p_g = \mathrm{e}^{-\beta \hbar \omega _0}, \end{aligned}$$

(32)

i.e., the Crooks relation for no-jump trajectories.

The trajectories with one jump yield $W=-2\hbar \omega _0,-\hbar \omega _0,0,+\hbar \omega _0$ or $+2\hbar \omega _0$. For instance, $W=-2\hbar \omega _0$ arises for the realizations, where the system starts in the excited state, makes one jump to the excited state, and is found eventually in the ground state. The probability of such a process is given by

$$\begin{aligned} P_1(-2\hbar \omega _0)= & {} \left\langle p_e \int _0^t d\tau \mathrm{e}^{-\Pi _e(\tau ,0;M_{\text {c}})}\Gamma _\uparrow (M_{\text {c}}) |c_e(\tau ,0;M_{\text {c}})|^2 \right. \nonumber \\&\left. \times \mathrm{e}^{-\Pi _e(t,\tau ;M_{\text {c}}+1)}|c_e(t,\tau ;M_{\text {c}}+1)|^2 \right\rangle _{M_{\text {c}}}. \end{aligned}$$

(33)

In this case, for $P_1(-2\hbar \omega _0)$ up to linear in $\Gamma$s, we may set $\mathrm{e}^{-\Pi _i(t_1,t_2;M_{\text {c}})}=1$, and drop the $\Delta \Gamma$ dependence in the populations yielding $|c_e(t_1,t_2;M_{\text {c}})|^2 =\sin ^2 (\pi (t_1-t_2)/2t)$, and

$$\begin{aligned} P_1(-2\hbar \omega _0)= & {} p_e \langle \Gamma _\uparrow (M_{\text {c}})\rangle _{M_{\text {c}}} \int _0^t d\tau \sin ^2 \left( \frac{\pi \tau }{2t}\right) \nonumber \\&\times \, \sin ^2\left( \frac{\pi (1-\tau /t)}{2}\right) = \frac{1}{8} \langle p_e\Gamma _\uparrow (M_{\text {c}})\rangle _{M_{\text {c}}}t. \end{aligned}$$

(34)

Similarly,

$$\begin{aligned} P_1(+2\hbar \omega _0)= \frac{1}{8} p_g \langle \Gamma _\downarrow (M_{\text {c}})\rangle _{M_{\text {c}}}t. \end{aligned}$$

(35)

Then,

$$\begin{aligned} \frac{P_1(-2\hbar \omega _0)}{P_1(+2\hbar \omega _0)}= \frac{p_e}{p_g}\frac{\langle \Gamma _\uparrow (M_{\text {c}})\rangle _{M_{\text {c}}}}{\langle \Gamma _\downarrow (M_{\text {c}})\rangle _{M_{\text {c}}}}. \end{aligned}$$

(36)

For equilibrium populations as here, $\langle \Gamma _{\uparrow ,\downarrow } (M_{\text {c}})\rangle _{M_{\text {c}}} = f(\pm \hbar \omega _0)$, and

$$\begin{aligned} P_1(-2\hbar \omega _0)/P_1(+2\hbar \omega _0)= \mathrm{e}^{-2\hbar \omega _0}, \end{aligned}$$

(37)

as expected.

One-jump trajectories leading to $W=\pm \hbar \omega _0$ are those where the system starts and ends in the same state, but makes one jump to the ground (excited) state in between. Therefore, for example, for $W=+\hbar \omega _0$, we have

$$\begin{aligned}&P_1(+\hbar \omega _0)\nonumber \\&\quad =\left\langle p_g \int _0^t d\tau \mathrm{e}^{-\Pi _g(\tau ,0;M_{\text {c}})}\Gamma _\downarrow |d_g(\tau ,0;M_{\text {c}})|^2 \mathrm{e}^{-\Pi _g(t,\tau ;M_{\text {c}}-1)}|c_g(t,\tau ;M_{\text {c}}-1)|^2 \right. \nonumber \\&\,\,\quad \left. +\, p_e \int _0^t d\tau \mathrm{e}^{-\Pi _e(\tau ,0;M_{\text {c}})}\Gamma _\downarrow |d_e(\tau ,0;M_{\text {c}})|^2 \mathrm{e}^{-\Pi _g(t,\tau ;M_{\text {c}}-1)}|d_g(t,\tau ;M_{\text {c}}-1)|^2 \right\rangle _{M_{\text {c}}}.\nonumber \\ \end{aligned}$$

(38)

With similar arguments as above, we find

$$\begin{aligned} P_1(+\hbar \omega _0)= \frac{3}{8} \langle \Gamma _\downarrow (M_{\text {c}})\rangle _{M_{\text {c}}}t, \end{aligned}$$

(39)

and analogously

$$\begin{aligned} P_1(-\hbar \omega _0)= \frac{3}{8} \langle \Gamma _\uparrow (M_{\text {c}})\rangle _{M_{\text {c}}}t, \end{aligned}$$

(40)

and thus

$$\begin{aligned} P_1(-\hbar \omega _0)/P_1(+\hbar \omega _0)= \mathrm{e}^{-\hbar \omega _0}, \end{aligned}$$

(41)

again as expected. We have thus shown that the Crooks relation is valid for processes linear in $\Gamma$s, i.e., zero- and one-jump trajectories. Collecting all these contributions, we have

$$\begin{aligned} P(-k\hbar \omega _0)/P(+k\hbar \omega _0)= \mathrm{e}^{-k\hbar \omega _0}, \end{aligned}$$

(42)

for $k=0,1,2$, and $P(W)\equiv P_0(W)+P_1(W)$.

Finally, Jarzynski equality is valid, since it (always) follows from Crooks equality. For our case of discrete values of W, it is seen by

$$\begin{aligned} \langle \mathrm{e}^{-\beta W} \rangle= & {} \sum _j P(W_j)\mathrm{e}^{-\beta W_j} = \sum _{k=-2}^2 P(k\hbar \omega _0) \mathrm{e}^{-k\hbar \omega _0} \nonumber \\= & {} \sum _{k=-2}^2 P(-k\hbar \omega _0) = \sum _j P(W_j) = 1. \end{aligned}$$

(43)