Skip to main content
SpringerLink
Log in

Single-projection procedure for linear optimization

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

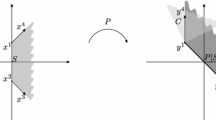
It is shown in this paper that under strict complementarity condition, a linear programming problem can be solved by a single orthogonal projection operation onto the cone generated by rows of constraint matrix and corresponding right-hand sides. The efficient projection procedure with the finite termination is provided and computational experiments are reported.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Floudas, C.A., Gounaris, C.E.: A review of recent advances in global optimization. J. Glob. Optim. 45(1), 3–38 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Shen, P.: Linearization method of global optimization for generalized geometric programming. Appl. Math. Comput. 162, 353–370 (2005)

    MathSciNet  MATH  Google Scholar 

  3. Meyer, C.D.: Matrix Analysis and Applied Linear Algebra, p. 718. SIAM, Philadelphia, PA (2000)

    Book  MATH  Google Scholar 

  4. Bersecas, D.P.: Nonlinear Programming 780. Athena Scientific, Nashua (2004)

    Google Scholar 

  5. Solodov, M.V., Svaiter, B.F.: A new projection method for variational inequality problems. SIAM J. Control Optim. 37, 765–776 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  6. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38(3), 367–426 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  7. Björck, A.: Numerical Methods for Least Squares Problems. SIAM, Philadelphia, PA (1996)

    Book  MATH  Google Scholar 

  8. Censor, Y.: Row-action methods for huge and sparse systems and their applications. SIAM Rev. 23, 444–466 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kaczmarz, S.: Angenherte Auflsung von Systemen linearer Gleichungen, Bulletin International de l’Acadmie Polonaise des Sciences et des Lettres. Classe des Sciences Mathmatiques et Naturelles. Srie A, Sciences Mathmatiques, v. 35, 355–357 (1937)

  10. Cimmino, G.: Calcolo approssimato per le soluzioni dei sistemi di equazioni lineari. LaRicerca Scientifica (Roma) 1, 326–333 (1938)

    MATH  Google Scholar 

  11. Agmon, S.: The relaxation method for linear inequalities. Can. J. Math. 6, 382–392 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  12. Motzkin, T.S., Schoenberg, I.J.: The relaxation method for linear inequalities. Can. J. Math. 6, 393–404 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  13. Censor, Y., Zenios, S.A.: Parallel Optimization: Theory, Algorithms, and Applications. Oxford University Press, New York (1997)

    MATH  Google Scholar 

  14. Rami, M.A., Helmke, U., Moore, J.B.: A finite steps algorithm for solving convex feasibility problems. J. Glob. Optim. 38(1), 143–160 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gould, N.I.M.: How good are projection methods for convex feasibility problems? Report no. NA-07/02 Numerical Analysis Group Oxford University Computing Laboratory Oxford University (see also Comput. Optim. Appl. 40, 1–12 (2008))

  16. Censor, Y., Chen, W., Combettes, P.L., Davidi, R., Herman, G.T.: On the effectiveness of projection methods for convex feasibility problems with linear inequality constraints. Comput. Optim. Appl. 51(3), 1065–1088 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Gould, N.I.M.: How good are extrapolated bi-projection methods for linear feasibility problems? Comput. Optim. Appl. 51(3), 1089–1095 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. Khachiyan, L.G.: A polynomial algorithm in linear programming. Soviet Math. Dokl. 20, 191–194 (1979)

    MATH  Google Scholar 

  19. Khachiyan, L.G.: Polynomial algorithms in linear programming. USSR Comp. Math. 20(1), 51–68 (1980)

    MathSciNet  MATH  Google Scholar 

  20. Deutsch, F., Hundal, H.: The rate of convergence for the cyclic projections algorithm I: Angles between convex sets. J. Approx. Theory 142(1), 36–55 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  21. Deutsch, F., Hundal, H.: The rate of convergence for the cyclic projections algorithm III: Regularity of convex sets. J. Approx. Theory 155(2), 155–184 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Xiua, Naihua: Jianzhong Zhangb Some recent advances in projection-type methods for variational inequalities. J. Comput. Appl. Math. 152, 559–585 (2003)

    Article  MathSciNet  Google Scholar 

  23. Bertsecas, D.P.: Extended Monotropic Programming and Duality, 18, Report LIDS—2692, (2010)

  24. Rockafellar, R.T.: Network Flows and Monotropic Optimization. Athena Scientific, Nashua (1998)

    MATH  Google Scholar 

  25. Von Hohenbalken, B.: A finite algorithm to maximize certain pseaudoconcave functions on polytopes. Math. Program. 13, 49–68 (1975)

    Article  Google Scholar 

  26. Wolfe, P.: Finding the nearest point in a polytope. Math. Program. 13, 49–68 (1976)

    MathSciNet  MATH  Google Scholar 

  27. Nurminski, E.A.: Convergence of the suitable affine subspace method for finding the least distance to a simplex. Comput. Math. Math. Phys. 45(11), 1915–1922 (2005)

    MathSciNet  Google Scholar 

  28. Calamai, P.H., Mori, J.J.: Projected gradient methods for linearly constrained problems. Math. Program. 39, 93–116 (1987)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Far Eastern Federal University, Vladivostok, Russia

    E. A. Nurminski

Authors
  1. E. A. Nurminski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. A. Nurminski.

Additional information

This research supported by the Russian Foundation for Basic Research Grant 13-07-12010.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nurminski, E.A. Single-projection procedure for linear optimization. J Glob Optim 66, 95–110 (2016). https://doi.org/10.1007/s10898-015-0337-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-015-0337-9

Keywords

Mathematics Subject Classification

Search

Navigation