Introduction

A fusion-fission reactor, considered by Bethe [1], Taczanowski [2], Manheimer [3] and others, is a combination of a fusion reactor and a fast fission reactor aimed for energy production, breeding of new fissile material or transmutation of radioactive waste from fission plants. The fusion device within the hybrid reactor is a neutron source and a fission reactor core surrounds the fusion device. The fusion-fission reactor is a driven system, which means that the fission reactor core has an efficient neutron multiplication factor k eff less than unity [4], typically 0.9–0.97, whereas a non-driven fission reactor operates at k eff  = 1. In a fusion-driven system of the type considered here, the power output is mainly from the fission part, where the fusion part only contributes with about 1% of the total energy production [4–6]. For such a power producing device, this could reduce the requirements of the fusion Q factor by up to a factor of 100 or even more [6]. This suggests that even a low Q fusion device, with Q as low as 0.15, could be adequate for power production. Thereby, realization of a hybrid reactor is far less demanding than that of a pure fusion reactor, since the plasma confinement requirements are dramatically reduced. Other beneficial features are that the wall loads from plasma loss and neutron bombardment, which seriously limit the possibilities to realize a commercial fusion reactor [7], could be reduced by orders for a hybrid reactor.

Strong energy amplification by fission enables the use of several kinds of fusion devices as neutron sources, and that idea is being pursued by several groups. To mention some of them, the FDS Team [8] in China and Stacey et al. [9] in USA have considered tokamak hybrids with downscaled ITER parameters. Bethe [1] primarily considered mirror machines and breeding of fuel. The interest has gradually switched to the possibilities for transmutation and power production, where Taczanowski [2] has made early studies on tandem mirror hybrid aimed for power production and transmutation (incineration) of radioactive isotopes. Noack et al. has considered minor actinide burning based on the axisymmetric Gas Dynamic Trap (GDT) [4]. Demir et al. have performed studies on fission mantle concepts for catalyzed fusion [10].

Mirror machines have several beneficial properties for a fusion-fission device [1, 2], in particular a steady state operation. In addition, possibilities for large end “divertor” plates (provided by expanders beyond the confinement region), geometric simplicity, compactness, a fission mantle geometry that allows practically all the fusion neutrons to enter the fission mantle and radio frequency heating with antennas located outside the confinement region are other useful features for a fusion-fission scenario [6, 11]. For a mirror fusion reactor, an electron temperature T e in the order of 10 keV is a typical requirement for net power production, and this has been a major roadblock for the development of mirror fusion reactors. However, in a fusion-fission system with a high energy multiplication Q r , i.e. the ratio of fission to fusion power, the requirement on T e is reduced substantially [2, 5, 6]. We here extend previous studies on the Straight Field Line Mirror (SFLM) concept with magnetic coils and magnetic expander regions. The configuration, outlined in Ref. [6], has the possibility to reach Q r  ≈ 147 with maintained reactor safety margins, and efficient power production is then expected with T e around 500 eV which seems reachable for up scaled mirror machines. A possible scenario for increasing the electron temperature by magnetic expanders beyond the confinement region is also outlined in Ref. [6]. The method relies on plasma depletion in the expanders, without violating an MHD (magnetohydrodynamic) stability condition and a gyro-resonant loss cone instability. In addition, the proposed device is aimed to keep plasma loads on “divertor” plates in the expanders tolerable, it would be possible to operate the device in a wide range of plasma β and the neutron source shutdown could be arranged in milliseconds (in a tokamak, shutdown is longer than 15 s as restricted by induction currents). Monte Carlo calculations for this SFLM hybrid concept have been carried out in Ref. [11] where fission mantle properties were set. The present paper is based on the “near-term” option [11] described therein, which corresponds to a fixed thermal power production of 1.5 GW in steady state. The fusion power increases slowly from about 10–20 MW during the fuel cycle (defined as 311 days of steady state 1.5 GW power production), as a result of the slow decrease in Q r due to fission fuel burning during operation (as an alternative, operation at a fixed keff and a fixed fusion power of 10 MW could be possible with control rods [6]). The fission mantle will be loaded with fresh fuel once a year. Calculations predict that the first wall will have a tolerable heat load and a lifetime of about 30 years power production (311 days a year) before a 200 DPA (displacement per atom) limit is reached [11]. Power load on end tanks are tolerable with Q = 0.15 and 4 m wide expander tank radii. Also, safety cases concerning local boiling of coolant and void effects were examined [11].

In most aspects, a driven system would be safer than a critical fast reactor, but the hollow geometry with the vacuum region carries within it a risk for fuel relocation (core collapse) where the reactor may become supercritical, as pointed out in Ref. [2]. These kinds of reactor accident scenarios have not been studied in Ref. [11].

The desired properties listed above would require appropriate device geometry, without holes for diagnostics and antenna power feeding in the fission mantle located in between the vacuum chamber and the superconducting magnetic coils. The aim is to show that a suitable coil design is possible within geometric and other constraints. The version outlined here is aimed for 1.5 GW thermal power (about 500 MW continuous electric power) with a confinement length of 25 m and a 40 cm midplane plasma radius [6, 11].

The design of magnetic field in a long-thin approximation for a fusion-fission hybrid reactor is carried out. Focus is on achieving MHD stability with the flux tube ellipticity within a tolerable range and keeping the gradients of the fields sufficiently low. Superconducting coils represented by filamentary line currents to reproduce the optimized field are generated. Early work on coil design has been made by Riordan et al. [12], who optimized ellipticity for MHD stable multiple mirrors. D’ippolito et al. [13, 14] made an optimization approach for tandem mirrors where omnigenuity and neoclassical transport were addressed.

Various coil systems have been developed for mirror machines, including MARS at Lawrence Livermore [15] and GAMMA 10 at Tsukuba [16, 17], where Gamma 10 uses a combination of baseball coils, racetrack coils and circular coils and MARS uses Yin-Yang coils and circular coils. Large superconducting coils have been developed in the Large Coil Task (LCT) [18], and will be manufactured for the ITER tokamak [19]. The machines with most challenging coil designs are stellarators [20].

In “Geometry of the Studied Test Device”, the reactor geometry is defined. The magnetic field is optimized in “The Vacuum Magnetic Field Properties” and appropriate coils for the optimized field are computed in “Calculation for Coil System”. The results are discussed in the fifth section and the last section concludes the paper.

Geometry of the Studied Test Device

The machine under consideration is a single cell minimum-B mirror with a mirror ratio of four. The magnetic field modulus is 2 T at the center of the mirror. The plasma radius is about 40 cm at the midplane, and the radius of the vacuum chamber is 90 cm, possibly with some small elliptic deformation around the maximum ellipticity regions to fit in the plasma edge. The length of the confinement region is set to 25 m, and beyond this 6.25 m long magnetic expanders with recirculation regions are added at each side, giving a total length of 37.5 m. The axial scale length z end = 12.5 m is the distance from the midplane to the end of the confinement region. The 26 m long fission mantle is symmetrically placed along the magnetic axis, and the outer radius of this mantle is 1.95 m [11]. However, the neutron shielding for the coils is not present in Ref. [11], and must be added. In a work by Yapici et al. [10], 5 cm of Boron carbide (B4C) is added for neutron shielding. Since no shielding calculations have yet been performed on the device considered here, some margin is applied and the total outer radius of the fission mantle is set to 2.10 m. This also gives space for some extra structure material if this is needed.

Beyond the fission mantle along the z direction, space is needed for power feed to ion cyclotron resonance heating and outflow of coolant from the fission mantle. Thus, no large coils are allowed in the area between \( \left| z \right| = 14.7 \) and \( \left| z \right| = 16\,{\text{m,}} \) although quadrupolar coils parallel with the z axis will be accepted. In the nearly neutron free transition region to the expander, between \( \left| z \right| = 16 \) and \( \left| z \right| = 17.5\,{\text{m,}} \) there is only a thin neutron shield and the vacuum vessel between the coils and the plasma. Beyond the transition region, the magnetic expander with divertor plates is located, and here cusp coils are placed.

The thickness of the superconducting coils can be approximated by using an average current density from an existing coil system. For comparison with copper coils, an engineering constraint on the maximum current density limited by cooling constraints is set to 15 kA/cm2 in a work by Miner et al. [20]. For superconducting coils, the conductor part of the ITER toroidal field cable-in-conduit coils is used as a reference. These have a cross section of approximately 0.85 m2 and each coil carries about 11,500 kA [19]. This gives an approximate current density of 1.35 kA/cm2 for the entire ITER toroidal field coil. JT-60 has approximately the double current density [21] and a somewhat conservative approach is to use 1.5 kA/cm2 which will be used in this study. An approximation of the structural material is made by again comparing with the ITER and JT-60 toroidal field coils [19]. They both have a cover of structure material with a thickness of about 10% of the width of the coils. Therefore, the coils will be approximated as having 20% extra width evenly distributed outside the conductor region. The approximations of the coil dimensions are quite coarse since this thickness does not scale linearly with size and since both the forces and the tolerable current density depend on the magnetic field. The coil cross section is square-shaped. The machine is outlined in Fig. 1.

Fig. 1
figure 1

A 3D view of the theoretical device studied in this paper, with fission mantle, coolant outflow pipes and magnetic expanders at the ends

Full size image

The size of the machine is determined from several aspects. Strong magnetic field gradients are harder to produce with a thick fission mantle, which makes the coil system for a long-thin machine easier to build. The plasma radius needs to be wide enough to give sufficient plasma volume for power production and to confine alpha particles, and is set to 40 cm. A long-thin plasma column is achieved with a 25 m long confinement region. A fusion power of 10 MW which corresponds to a neutron production of 3.6 × 1018 neutrons per second could give almost 1.5 GW thermal power output with Q r  ≈ 150. The 1.2 m thick fission mantle provides enough space for fission materials, protection of first wall from fission neutrons, neutron reflectors, tritium reproduction and neutron shielding of magnetic coils. An available empty space could be used for control rods or adding of fission fuel if required [11]. With ion cyclotron heating antennas located outside the confinement region, it is possible to avoid holes in the fission mantle, whereby almost all fusion neutrons enters the fission mantle and a very high Q r (Q r  ≈ 150) is possible with reactor safety margins [11]. Plasma is accessible only through the mirror ends.

The Vacuum Magnetic Field Properties

The vacuum magnetic field is optimized using the following criteria:

  1. 1.

    The field is designed to avoid gross MHD instabilities. The average minimum B criterion was derived by Rosenbluth et al. [22] and is equivalent to a favorable average curvature of the field lines. Later the criterion was experimentally verified by Ioffe [23], demonstrating a striking stabilization of gross MHD modes and improvement in plasma confinement by a sufficiently strong quadrupolar field. The flute stability criterion [24] which in the low β limit can be written as

$$ {\frac{\partial }{{\partial r_{0} }}}\int {\frac{pdl}{B}} \le 0 $$
(1)

is a pressure weighted field line curvature criterion and will here be used to determine stability, where \( p = p_{\parallel } + p_{ \bot } \) is the sum of the parallel and perpendicular (with respect to the magnetic field line) pressure tensor components. However, since the details of the pressure profile is not known beforehand and depend on the magnetic field, a stability margin to the criterion (1) will be used.

  1. 2.

    The magnetic flux tube ellipticity should be minimized. A high ellipticity, caused by the stabilizing quadrupolar field, could give impractically thin flux tubes near the mirrors (in the thin direction) and may for strongly elliptic regions give alpha particle gyro radii exceeding this thin width. Also, highly elliptic plasmas will produce a slightly angular-dependent neutron flux, which may be somewhat unfavorable for the fission mantle, although the fission mantle will smear this out.

  2. 3.

    Too strong gradients in the field components in the z direction has to be avoided to find a practical coil set residing outside the fission mantle that produces those field components in the plasma confinement region. The thick fission mantle makes the coil design problem much harder since the distance between the coils and the plasma increases significantly.

There are also additional parameters that are relevant for the optimization. Neoclassical radial plasma losses are often addressed [14]. However, since the confinement time in a fusion-fission device can be much shorter than in a pure fusion reactor, axial losses are expected to dominate and radial losses are neglected. Large magnetic expanders are required to ensure tolerable plasma axial power load on the wall. A list with numerous requirements to be addressed for tandem mirror design has been given by Baldwin [15]. However, the present study is limited to the three properties stated above. These requirements are somewhat contradicting, and the task is to find a solution that is a suitable compromise for all requirements.

A field satisfying the stability and ellipticity criteria, the Straight Field Line Mirror (SFLM) which is a marginal minimum B vacuum field, has been derived in Ref. [25] which satisfies marginal minimum-B stability has been derived by Ågren and Savenko [25]. This SFLM field have however inconveniently strong gradients near the mirror ends for moderately high values of the mirror ratio. Also, that field does not have a natural end of the mirror, since \( \partial B/\partial z^{2} \) is monotonically increasing away from the midplane. Thus, this field can not constitute the mirror field over the entire domain and has to be concatenated with some other field at some region before the mirror ends. Although such a concatenated field has beneficial properties at the central section, it is not obvious that the total solution has optimal properties with respect to our criteria listed above (or even satisfies them).

Derivation of the expressions for these criteria has been made in earlier work (see for example Ref. [26]) and is repeated here for clarity. The derivation starts from the magnetic scalar potential

$$ \phi_{m} = \int\limits_{0}^{z} {\tilde{B}dz - {\frac{{x^{2} + y^{2} }}{4}}} \tilde{B}^{\prime} + {\frac{{x^{2} - y^{2} }}{4}}g(z) + o(\lambda^{4} ) $$
(2)

for the vacuum magnetic field B = ∇ϕ m which satisfies Laplace equation to zeroth order in λ. The magnetic field components are

$$ B_{x} = \frac{x}{2}(g - \tilde{B}^{\prime}), $$
(3)
$$ B_{y} = - \frac{y}{2}(g + \tilde{B}^{\prime}), $$
(4)
$$ B_{z} = \tilde{B} + {\frac{{x^{2} }}{4}}\,{\frac{{d(g - \tilde{B}^{\prime})}}{dz}} - {\frac{{y^{2} }}{4}}\,{\frac{{d(g + \tilde{B}^{\prime})}}{dz}} $$
(5)

where \( \tilde{B} \) is the magnetic field on the z axis. The magnetic field B = B 0 ∇r 0 × ∇θ0 where B 0 is the magnetic field at x = y = z = 0, can also be described by the Clebsch coordinates r 0 , θ0, which are constant along B. To calculate the flute stability criterion in (1), which involves the derivative \( \partial B(\phi_{m} ,r_{0} ,\theta_{0} )/\partial r_{0} \), a transformation to flux coordinates is made. Clebsch coordinates x 0 = r 0 cosθ0 and y 0 = r 0 sinθ0 are introduced by B = B 0∇x 0 × ∇y 0, where the constant B 0 is the magnetic field modulus at the origin. Since x 0 and y 0 are constant along B, the Clebsch coordinates can be determined by tracing curves (x(z), y(z), z) parallel to the magnetic field lines,

$$ x(z) = x_{0} e^{{\int_{0}^{z} {h_{1} (z^{\prime } )dz^{\prime } } }} + {\rm O}(\lambda^{3} ), $$
(6)
$$ h_{1} (z) = {\frac{{g - \tilde{B}^{\prime } }}{{2\tilde{B}}}} = {\frac{1}{{\tilde{B}}}}\,{\frac{{B_{x} }}{x}} + {\rm O}(\lambda^{2} ) $$
(7)
$$ y(z) = y_{0} e^{{\int_{0}^{z} {h_{2} (z^{\prime } )dz^{\prime } } }} + {\rm O}(\lambda^{3} ), $$
(8)
$$ h_{2} (z) = - {\frac{{g + \tilde{B}^{\prime } }}{{2\tilde{B}}}} = {\frac{1}{{\tilde{B}}}}\,{\frac{{B_{y} }}{y}} + {\rm O}(\lambda^{2} ) $$
(9)

To leading order flux surfaces, determined by \( r_{0}^{2} (x,y,z) = {\text{const}} \) with circular cross section at z = 0 are the ellipsoids

$$ r_{0}^{2} = x^{2} e^{{ - 2\int_{0}^{z} {h_{1} (z^{\prime } )dz^{\prime } } }} + y^{2} e^{{ - 2\int_{0}^{z} {h_{2} (z^{\prime } )dz^{\prime } } }} $$
(10)

Flux coordinates x 0, y 0, ϕ m are determined by

$$ x_{0} (x,y,z) = xe^{{ - \int_{0}^{z} {h_{1} (z')dz'} }} + {\rm O}(\lambda^{3} ) $$
(11)
$$ y_{0} (x,y,z) = ye^{{ - \int_{0}^{z} {h_{2} (z')dz'} }} + {\rm O}(\lambda^{3} ) $$
(12)
$$ \phi_{m} (x,y,z) = \phi_{m,0} (z) + {\frac{{x^{2} }}{2}}\tilde{B}h_{1} + {\frac{{y^{2} }}{2}}\tilde{B}h_{2} + {\rm O}(\lambda^{4} ) $$
(13)

where \( h_{1} + h_{2} = - \tilde{B}^{\prime}/\tilde{B} \) and \( \phi_{m,0} (z) = \int_{0}^{z} {\tilde{B}dz} \) is the scalar magnetic potential on axis. It is convenient to substitute ϕ m (x) with an arc length-like variable \( \tilde{s}({\mathbf{x}}) \) by \( \phi_{m} (\tilde{s}) \equiv \int_{0}^{{\tilde{s}}} {\tilde{B}(\tilde{s})d\tilde{s}} = \phi_{m,0} (\tilde{s}) \). At the z axis \( \tilde{s}({\mathbf{x}}) \) coincides with the arc length of the magnetic field lines, but away from the axis \( \tilde{s}({\mathbf{x}}) \) differs from the arc length of the magnetic field line by correction terms of order λ2. Using the inverse function \( \tilde{s}({\mathbf{x}}) \equiv \phi_{m,0}^{ - 1} [\phi_{m} ({\mathbf{x}})] \), we obtain

$$ \tilde{s}(x,y,z) = z + {\frac{{x^{2} }}{2}}h_{1} + {\frac{{y^{2} }}{2}}h_{2} + {\rm O}(\lambda^{4} ) $$
(14)

and \( {\mathbf{B}} = \nabla \phi_{m} (\tilde{s}) = \tilde{B}(\tilde{s})\nabla \tilde{s} \) gives with \( \tilde{B}(\tilde{s}) > 0 \)

$$ B = \tilde{B}(\tilde{s})\left[ {1 + {\frac{{x^{2} }}{2}}\left( {h_{1}^{2} + {\frac{{dh_{1} }}{dz}}} \right) + {\frac{{y^{2} }}{2}}\left( {h_{2}^{2} + {\frac{{dh_{2} }}{dz}}} \right)} \right] + {\rm O}(\lambda^{4} ) $$
(15)

Expressed in the flux coordinates \( (\tilde{s},r_{0} ,\theta_{0} ) \), this becomes apart from λ4 corrections

$$ B(\tilde{s},r_{0} ,\theta_{0} ) = \tilde{B}(\tilde{s}) + {\frac{{r_{0}^{2} }}{2}}[u_{1} (\tilde{s})\cos^{2} \theta_{0} + u_{1} (\tilde{s})\sin^{2} \theta_{0} ] $$
(16)

where

$$ u_{1,2} (\tilde{s}) = \tilde{B}(\tilde{s})e^{{2\int_{0}^{{\tilde{s}}} {h_{1,2} (\tilde{s}\prime )d\tilde{s}\prime } }} \left[ {h_{1,2}^{2} (\tilde{s}) + {\frac{{dh_{1,2} (\tilde{s})}}{{d\tilde{s}}}}} \right] $$
(17)

The flute stability criterion

$$ {\frac{\partial }{{\partial r_{0} }}}\int {\frac{pdl}{B}} = - \int {{\frac{{p\partial B/\partial r_{0} }}{{B^{2} }}}d\tilde{s}} + o(\lambda^{2} ) \le 0 $$
(18)

where the integration is along a magnetic field line, simplifies in the near axis approximation to

$$ W_{1} \cos^{2} \theta_{0} + W_{2} \sin^{2} \theta_{0} \ge 0 $$
(19)

where

$$ W_{1,2} (z_{\text{end}} ) = \int\limits_{{ - z_{\text{end}} }}^{{z_{\text{end}} }} {{\frac{pdz}{{\tilde{B}(z)}}}} e^{{2\int_{0}^{z} {h_{1,2} (z^{\prime } )dz^{\prime } } }} \left[ {h_{1,2}^{2} (z) + {\frac{{dh_{1,2} (z)}}{dz}}} \right] \ge 0 $$
(20)

With the symmetry relations \( \tilde{B}( - z) = \tilde{B}(z) \) and g(−z) = g(z), we obtain W 1 = W 2. The stability condition in (20) corresponds to the flute stability condition in Ref. [24] with electrically isolated end points. Due to a different boundary condition, the condition (20) differs somewhat from the corresponding average minimum B criterion for a periodic mirror given in Ref. [12].

The task is to find suitable g(z) and \( \tilde{B}(z) \) so that the maximum ellipticity is minimized while MHD stability is maintained. It is also necessary that it is possible to generate a coil set that closely reproduces those field profiles, which excludes profiles with too sharp gradients. The chosen method represents the two functions g(z) and \( \tilde{B}(z) \) with equidistant cubic clamped splines in the confinement region, where the cubic splines have continuous derivatives to second order. It is sufficient to model the fields in half the region (z > 0) with the assumed symmetries around the z = 0 plane. The boundary conditions are

$$ \tilde{B}(0) = B_{0} , $$
(21)
$$ \tilde{B}(L) = R_{m} B_{0} , $$
(22)
$$ \tilde{B}^{\prime}(0) = 0, $$
(23)
$$ \tilde{B}^{\prime}(L) = 0 $$
(24)

for the \( \tilde{B}(z) \) field, where the two first can be prescribed by setting the first and the last spline knot to the actual values. The boundary conditions on the derivatives can be prescribed with a clamped spline representation. Correspondingly, the g(z) function has the prescribed boundary condition \( g^{\prime}(0) = 0 \), while \( g^{\prime}(L) \) can be chosen freely. Since the maximum ellipticity should be minimized it is likely that a rapidly decreasing \( g(L) \) is beneficial. For \( \left| z \right| > z_{\text{end}} \), magnetic expanders (with favorable curvature) are expected to add to stability, as well as line tying effects. Favorable stability properties in the region \( \left| z \right| < z_{\text{end}} \) ought therefore to be sufficient to ensure gross MHD stability.

One way to find the functions g(z) and \( \tilde{B}(z) \) (with a spline representation) is by using a numerical local optimization method by minimizing a functional \( f(\tilde{B},g) \)

$$ \begin{aligned} f =\,K_{s2} \int\limits_{0}^{{z_{\text{end}} }} {W_{1}^{2} (z^{\prime } )dz^{\prime } } - K_{s1} \int\limits_{0}^{{z_{\text{end}} }} {W_{1} (z^{\prime } )dz^{\prime } } - K_{\text{aneg}} K_{s1} \int\limits_{0}^{{z_{\text{end}} }} {W_{1} (z^{\prime } )H( - W_{1} (z^{\prime } ))dz^{\prime } } \\ & + K_{\text{ell}} \varepsilon (z_{\max } ) + K_{\text{ripple}} \int\limits_{0}^{{z_{\text{end}} }} {\left| {{\frac{{dg(z^{\prime } )}}{{dz^{\prime } }}}} \right|} dz^{\prime } \\ \end{aligned} $$
(25)

where K s2, K s1, K aneg, K ell and K ripple are weight constants for stability discrepancies from marginal stability, stability, extra punishment for negative stability, ellipticity and the integrated absolute value of the derivative of g(z) which suppresses ripple and peaked profiles. H denotes Heavisides step function. After the optimization procedure, gross stability is checked by plotting W 1(z). The minimization is performed using the spline knots as variables and the start and end points for \( \tilde{B} \) and g′(L) are input parameters. The optimization worked well for neutral pressure profiles (i.e. with constant p), but when a representative pressure profile with sloshing ion peaks was inserted the optimizer created undesired “bumps” in the field to get a good curvature at the sloshing ion peak. These “bumps” made the pressure profile unrealistic, since \( \partial B/\partial z \) became almost zero in the sloshing ion region. Although different punishing terms of first and second derivatives in the sloshing ion region was added, the problem was not solved. In order to solve this problem, the p function could be chosen as some prescribed function of \( \tilde{B} \). This problem is left for future work, and the straight field line mirror field is used in the central region. At \( \left| z \right| = 8.75 \) the straight field line mirror field was concatenated with another field to end the mirrors. This outer part of the field was modelled with a spline representation. It proved to be best not to optimize this field with an optimization function but instead moving the spline points individually by hand to avoid ripple once optimization had been tested and the behaviour had been observed. The resulting field has several beneficial properties. The region of bad curvature is rather small (the negative derivative regions in the W 1 integral in Fig. 2) and is expected to be at the beginning of the sloshing ion peaks. The good curvature region is expected to be at the sloshing ion peak. In Fig. 2, the W 1 integral is shown with both a neutral pressure profile and a representative sloshing ion distribution. The pressure profile is not yet determined, but with this field there is a quite large margin on stability, and the field is expected to be stable for most representative pressure profiles in the low β limit.

Fig. 2
figure 2

Profiles for a \( \tilde{B}(z), \) b g(z), c W 1(z) for a sloshing ion distribution and for a constant pressure function, d ellipticity and e pressure of a chosen representative sloshing ion distribution for the selected magnetic field for the fusion-fission reactor

Full size image

Calculation for Coil System

To reproduce the magnetic field selected in the previous section, a set of superconducting coils with specified currents are defined. The problem is simplified by using a filamentary set of line currents for each coil. A current density value of J max = 1.5 kA/cm2 is used to determine the size of the superconducting coils. The spatial distribution of coils is limited by the condition that the coils must reside outside the fission mantle and neutron shielding due to heating from neutrons. The distance to the z axis from the coils are therefore larger than in a fusion reactor (with the same fusion device), which makes it harder to produce sharp relative derivatives \( \partial /\partial z(\ln \tilde{B}) \) and \( \partial /\partial z(\ln g) \). It is in principal possible to create sharp relative derivatives by cancelling fields (with opposing currents in nearby coils), but such a method would be uneconomic and less accurate [27]. Also, the coils are not allowed to intersect.

Since the field components are defined near the z axis, the optimization has been made along this line. Noting that the magnetic field is defined by the two functions g(z) and \( \tilde{B}(z) \), a convenient way to reproduce the field is to separate the problem into one optimization problem for g(z) and another for \( \tilde{B}(z) \). This is arranged by selecting a suitable coil set, where axisymmetric coils reproduces \( \tilde{B}(z) \) and a particular set of quadrupolar coils reproduces g(z). Yin-Yang coils [28] may be capable of reproducing the optimized field, but a coil similar to a baseball coil [29] with quadrupolar symmetry which will not add to the \( \tilde{B}(z) \) field at the z axis is used instead to fully separate the problem. Since the quadrupolar field is harder to create, the thinner quadrupolar coils will be placed inside the circular coils.

The optimizations are heavily weighted for the confinement region, and the comparatively large relative errors in the recirculation and expander regions are assumed less important, since the design is aimed for a very low plasma density in this region. The field profiles for the recirculation region and the magnetic expander are only chosen by the loose criteria that g(z) shall change sign shortly beyond the mirror end to limit maximum ellipticity and that the field shall be recirculated and thus returning the ellipticity to about unity at the expander end. Also, g(z) has to be weak in the expander and \( \tilde{B}(z) \) shall be weak with positive curvature at the end of the expander to provide added stability. If a more detailed recirculation and expander region are modelled, the optimization should be weighted differently. Also, it is probably necessary to have in situ adjusted weak correction coils at the expander to distribute the heat load on the divertor plates correctly, since the magnetic field here is very weak and thus a large cancellation in magnetic field accuracy is present.

To produce \( \tilde{B}(z) \), the simplest choice is to use a set of circular coils with varying radius, current and position. By symmetry, it is sufficient to specify the coils on one side of the mirror. The ith axisymmetric coil is divided into k c  = 100 squared cross sections with a line current I i /k c in the center of each such cross section, and thus \( \tilde{B}_{c} (z) \) from the coils is

$$\tilde{B}_{c} = {\frac{{\mu_{0} }}{2}}\sum\limits_{i}\sum\limits_{j = 1}^{{k_{c} }} {\frac{{I_{i} }}{{k_{c}}}}r_{i,j}^{2} \\\times\left( {{\frac{1}{{\left[ {r_{i,j}^{2} + (z - z_{i,j})^{2} } \right]^{3/2} }}} + {\frac{1}{{\left[ {r_{i,j}^{2} +(z + z_{i,j} )^{2} } \right]^{3/2} }}}} \right)$$
(26)

where r i,j and z i,j denotes radius and z position for the jth filamentary current element in the ith coil pair. The width of the conductor part of the coil is calculated from I i as

$$ b = \sqrt {{\frac{{I_{i} }}{{J_{\max } }}}} $$
(27)

The radius r i,j is calculated as

$$ r_{i,j} = r_{\text{plasma}} + r_{\text{fission}} + r_{\text{quad}} + 0.1b + \Updelta r_{i,j} $$
(28)

where r plasma, r fission, r quad and Δr i,j are the vacuum vessel radius, the fission mantle thickness, the quadrupolar coil thickness and the radial distance added from the filamentary representation. A functional

$$ f_{z} = \int\limits_{0}^{{z_{\max } }} {dz\left[ {1 + K_{c} H(1 - \left| {\bar{z}} \right|)} \right]{\frac{{\left[ {\tilde{B}(z) - \tilde{B}_{c} (z)} \right]^{2} }}{{\tilde{B}^{2} (z)}}}} + K_{i} \sum\limits_{i} {r_{i} I_{i}^{2} } + K_{{c,{\text{ripple}}}} \int\limits_{0}^{{z_{\text{end}} }} {\left| {{\frac{{d\tilde{B}_{c} (z)}}{dz}}} \right|} dz $$
(29)

where K i is a weight factor for a power term, K c is used to strengthen the importance of the confinement region and K c,ripple is used to punish ripple, is used for minimization in the optimization process. The power term may not be correct for superconducting coils, but it still fulfills its purpose to restrain a waste of current to gain accuracy. To have a current restricting term is crucial; otherwise very strong currents in both directions are produced.

The optimization is made using a Nelder-Mead numerical local optimization method. During optimization, different approaches have been tried. First, r i , I i and z i for each coil were used as free parameters with certain constraints. It proved however difficult to get a spatially acceptable result. The best result was achieved by keeping r i constant and restraining z i to a small region around the initial value to prevent coils from intersecting. In order to find a fairly good local minimum, a search was made with randomized initial values and k c  = 1 for hundreds of starting points. The initial values of the best result was then used as a seed for the optimization with k c  = 100. This showed that a lot of minima existed, and that those minima differed at least with a factor of 3 for the value of the functional (29).

The resulting field \( \tilde{B}_{c} (z) \) deviates about 0.2% from \( \tilde{B}(z) \) at the worst points within the major part of the SFLM region. In the spline region, the maximum errors are about 1.5%. These errors are however not expected to be very important and should not be viewed as a typical ripple since the field has a strong gradient in this region. Also, the concatenation point is visible, indicating that the derivative \( \partial B/\partial z \) has a slight discontinuity. One should though keep in mind that the rippling error contributes to \( \tilde{B}^{\prime}_{c} (z) \), causing a larger error in B c,x /x and B c,y /y. Outside the confinement region, the relative errors are much larger due to a large K c . The relative errors and the resulting field are presented in Fig. 3.

Fig. 3
figure 3

The \( \tilde{B}(z) \) produced by the circular coils, where a, b show the relative error in the field and c the field itself

Full size image

For the quadrupolar field component g(z), several different coil geometries may be used. First, four shape-optimized conductors with quadrupolar symmetry described by a function r(z) was applied [27]. This approach gave, however, spatially unpractical solutions with large relative errors. It proved to be better to use an array of cage-like coils where each coil constitutes of four straight parallel conductors in the z direction with quadrupolar symmetry and four quarter-circle segments at each end connecting those conductors (for simplicity, sharp corners are used). The four quarter-circle segments form a circular coil, but the direction of the current shift so that nearby parts have opposite current directions and thereby fulfilling quadrupolar symmetry. In the array, the quarter-circle segments carry a current that is half of the difference of the currents of the surrounding straight segments. A similar coil concept was proposed by Riordan et al. [12]. Note that if only two opposing quarter-circle segments are used to connect the straight conductors, the coil roughly resembles a squared baseball coil. A 3D-picture of an array of quadrupolar coils is shown in Fig. 4.

Fig. 4
figure 4

3D-view of an array of three quadrupolar coils with varying currents

Full size image

Only one side of the mirror needs to be parameterized during optimization due to symmetry. The contributions from such a coil to the quadrupolar field can be grouped as contributions from sets of four straight conductors \( g_{c,s} \) and contributions from sets of four-quarter-circle segments \( g_{c,c} \), where

$$ g_{c,s} = {\frac{{3\mu_{0} I_{1} }}{\pi }}\int\limits_{{z_{1} }}^{{z_{2} }} {{\frac{{r^{\prime 2} dz^{\prime } }}{{[(z - z^{\prime } )^{2} + r^{\prime 2} ]^{5/2} }}}} = - {\frac{{3\mu_{0} I_{1} }}{\pi }}\left[ {K(z - z_{2} ) - K(z - z_{1} )} \right] $$
(30)

where

$$ K(z^{\prime } ) = {\frac{{[3r^{\prime 2} + 2z^{\prime 2} ]z^{\prime } }}{{3r^{\prime 2} [r^{\prime 2} + z^{\prime 2} ]^{3/2} }}} $$
(31)

and

$$ g_{c,c} = \pm {\frac{{3\mu_{0} I_{1} /2}}{\pi }}\,{\frac{{r^{\prime 2} (z - z^{\prime } )}}{{[(z - z^{\prime } )^{2} + r^{\prime 2} ]^{5/2} }}} $$
(32)

to zeroth order in r. I 1 denotes the current in the straight conductors, with a positive sign for currents that give a positive contribution to g(z), and r′ is the coil radius. For g c,c in (32), a positive sign shall be taken for coils with positive, inner z′ and negative, outer z′. The other two rings have a negative sign. The g(z) field from one such coil is seen in Fig. 5.

Fig. 5
figure 5

The g(z) field from one quadrupolar coil with end points at z = ±0.5 and radius of 0.4, where the contributions from the different parts of the coil are shown

Full size image

Each coil segment has been divided into filamentary line currents. The quarter-circle segments have been divided into k q filamentary line currents in the same manner as with the circular coils, where k q  = 100 in this study. For the straight coil segments, k q filament segments are used as well. The angular difference between the line from the z axis to the center line of the straight coil segment and the corresponding line to the filamentary current, φ q , modifies the contribution from the straight bars to the g(z) function in (30) with a factor of cos(2φ q ) when the symmetry is regarded. The optimization has been performed in a similar manner as with the circular coils. A Nelder-Mead numerical local optimization function has been used, and the same random search algorithm for a fairly good starting point for the optimization as for the circular coils was applied. As free parameters, both the currents and the z coordinate of the rings in the array are used where the z position for each ring is restrained to a prespecified interval. The inner radius of all quadrupolar coils was set to the outer radius of the fission mantle, 2.1 m. The functional

$$ f_{q} = \int\limits_{0}^{{z_{\max } }} {dz\left[ {1 + K_{c,q} H(1 - \left| {\bar{z}} \right|)} \right]} {\frac{{\left[ {g(z) - g_{c} (z)} \right]^{2} }}{{g^{2} (z)}}} + K_{i,q} \sum\limits_{i} {(I_{i}^{2} l_{i,s} + I_{i,c}^{2} l_{i,c} )} $$
(33)

where K c,q is used to strengthen the importance of the accuracy in the confinement region and K i,q represents some current restricting term is used for minimization by the optimizer. For the ith coil, I i denotes the current in the straight bars, I i,c denotes the current in the quarter-circle segments, l i,s is the total length of the straight bars and l i,c is the total length of the four quarter-circle segments. Also, a very small strengthening term for g(z) is applied in the optimization to lift up the average value of the ripple a little bit above zero to grant stability.

The resulting g(z) has typically 1–1.5% relative errors in the confinement region and up to 10% at the peak value where the peak is slightly rounded off. This rounding off is expected to be of very small importance. Outside the confinement region is the relative error much larger. It is also worth noting that ripple in g(z) does not have the same impact as ripple in \( \tilde{B}(z) \) for the relative errors in B x and B y . The resulting profiles are shown in Fig. 6.

Fig. 6
figure 6

The g(z) produced by the quadrupolar coils, where a, b show the relative error in the field and c the field itself

Full size image

When adding the two coil sets, the ideal x and y components of the magnetic field are presented in (3–4) to first order in r. Since \( \tilde{B}^{\prime}(z) \) is odd and g(z) even, there will be a cancellation on one side of the mirror for both the x and y magnetic field components. Thereby, since \( \tilde{B}^{\prime}(z) \) and g(z) are of the same order of magnitude, the relative errors (but not the absolute errors) of the x and y components will be strongly increased on that side. Also, the relative error of \( \tilde{B}^{\prime}(z) \) is considerably larger than the relative error of \( \tilde{B}(z) \) due to the ripple. However, in the confinement region, the relative errors are still on an acceptable level and the coils have actually smoothened the ideal field in the region where cancellation occurs. The x component of the magnetic field is shown in Fig. 7.

Fig. 7
figure 7

The x component of the magnetic field divided by x from the entire coil set near the z axis

Full size image

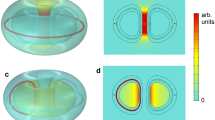
With this set of coils, MHD stability and ellipticity is examined. The W 1 stability function (with a neutral pressure profile and a representative sloshing ion distribution) and εell ellipticity function are calculated from the coils and displayed in Fig. 8. As can be seen, W 1 has a ripple that comes from the discrete coils and deviates from the ideal field. However, near the sloshing ion peak, the behaviour is roughly the same, with good and bad curvature located at the same spots. Figure 8 also shows the gross stability increase in the magnetic expander and the ellipticity which has a maximum of about 20.

Fig. 8
figure 8

Results for the entire coil set, where a–c shows the stability function W 1 with the pressure function from Fig. 2 in (a) and constant pressure for (b, c). In d the ellipticity for the entire coil set is shown. Note the strong stabilization provided by the magnetic expander in (c)

Full size image

Results and Discussion

The magnetic field has been optimized for MHD stability, low ellipticity and low field gradients, where a stability margin has been requested since the details of the pressure profile is not known at present. A problem of designing the magnetic field for a fusion-fission reactor is harder that that for a fusion reactor. It is crucial to find a magnetic configuration with low field gradients, since the coils that should produce the field are placed outside the thick fission mantle and are located far from the plasma. Therefore, the gradient steepness along the z direction determines a minimum length of the machine. The initial idea was to use the SFLM field [25] concatenated with some other field near the mirror ends. However, it turned out that the SFLM field had inconveniently strong gradients near the mirror ends, and the concatenation point therefore ended up at \( \left| z \right| = 8.75 \). In another approach the axisymmetric and quadrupolar field was modelled with a spline representation for the optimization. With a constant pressure profile, e.g. using the average minimum B criterion, this approach worked well. However, when a representative sloshing ion distribution was used the optimizer created undesired “bumps” in the g and \( \tilde{B} \) functions in order to create good curvature at the sloshing ion peaks. The consequence of this is that the \( \tilde{B} \) function flattens out at the sloshing ion peak which makes it impossible to create such a pressure profile for equilibrium reasons. To address this problem the pressure profile could be modelled as some function of \( \tilde{B} \), which is left for future studies. The chosen method was to use the concatenated SFLM field and to model the ending fields with splines. The ending field was optimized manually by moving the spline points once the behavior had been examined.

The resulting optimized field has several beneficial properties. The field gradients are fairly low, the maximum ellipticity of about 20 is acceptable and there is a stability margin. The sloshing ion peak is expected to give a stronger contribution to the region of good curvature than to the region of bad curvature. Also, the expander region and line tying effects are expected to add to the stability margin. The SFLM field in the middle part of the confinement region is omnigenious, and although the ending field is not omnigenious the neoclassical radial losses are expected to be much smaller than the axial losses. Also, for a fusion-fission device, omnigenity is not as important as it would have to be for a pure fusion device, since the confinement time is expected to be determined by the axial loss. Concerning β-limiting ballooning modes, Ref. [30] indicates that they are probably not of great importance and this is left for future studies. Therefore, the SFLM field concatenated with a spline line optimized field is selected for the fusion-fission reactor in this study.

The coil set consists of 28 circular coils and an array of 25 quadrupolar coil segments. The coils with specified currents and sizes are listed in Table 1 for the circular coils and Table 2 for the quadrupolar coils. The entire coil set is shown in 3D in Fig. 9, and the circular coils are removed in Fig. 10. As seen from the tables and 3D images, no coils intersect each other, but the optimized inner radii of the circular coils nearly intersect the inner quadrupolar coils. There is room available for outflow/inflow of liquid lead–bismuth coolant, which is represented by the pipes in Figs. 9 and 10, and for power feed to the ion cyclotron resonance heating. There is also a large space of 1.33 m available around z = 0 that can be used for radial outflow/inflow of coolant as well as additional spaces for tritium-lithium outflow etc. In a region around the end of the confinement region, there are small possibilities of accessing the fission mantle and plasma due to the density of coils. The magnetic expander is produced by two cusp coils on each side. One quadrupolar coil on each side is located beyond the magnetic mirror and the expanders, which cancels out the g(z) function in the expander region.

Table 1 The circular coils on the positive z side, defined by inner radius, cross section center z coordinate, cross section width/height and current
Full size table
Table 2 The quadrupolar coils on the positive z side, defined by end z coordinate, cross section width/height of the straight bars, cross section width/height of the quarter-circle segments, current in the straight bars and current in the quarter-circle segments
Full size table
Fig. 9
figure 9

The mirror machine with the entire coil set, where the circular coils reside outside the quadrupolar coils. Space is available for outflow/inflow of coolant from the fission mantle and power feed to radio frequency heating in the transition regions between the confinement region and the magnetic expanders

Full size image
Fig. 10
figure 10

The mirror machine with the quadrupolar coils where the circular coils have been removed

Full size image

The ripples produced by the coils are not expected to give problems. Ref. [31] indicates that a ripple larger than 1% in \( \tilde{B} \) in the central region would give rise to ballooning modes. The ripple in the central region is however smaller than 1% and since Ref. [31] was written before Refs. [30] and [31] also points out at that time unpublished results in Ref. [30] this is not expected to be a problem. If so, use of ferromagnetic materials [31] is an option to substantially reduce the ripple.

For producing real superconducting coils, some filamentary current distribution with high resolution has to replace the low resolution filamentary line currents, where care should be taken regarding the connections between the quadrupolar coil segments, and some sharp turns have to be rounded off. Also, a deeper analysis concerning maximum forces and magnetic field strengths for maintaining superconductivity needs to be made, and higher order fields should be calculated to investigate the magnetic well radius. Also, the finite β diamagnetic effects should be taken into account. A strength with the obtained solution is that there is flexibility to independently control the currents in the quadrupolar and circular coils to adjust for finite β effects.

All optimizations in this paper are performed using local optimizers. A local optimizer finds local minima, which may or may not be good solutions to the problem, and which minima the optimizer will find depends on the initial values of the variables. The functionals minimized in this paper depend of many variables and at least the coil functionals have a large number of local minimas. It would be desirable to search the entire space for the global minima. It is however too many variables involved to make a grid search or similar, which indicates that some heuristic approach has to be made. There are many methods for global optimization available [32]. For stellarators, even genetic algorithms have been applied successfully [20]. This study is however limited to use of local optimizers, with some simple random search algorithm in the coil optimizations to search for a reasonably good initial iteration point. Since the representation of the coils is based on some rather coarse assumptions, a global optimization may anyway not be worthwhile until those assumptions have been clearly specified.

Conclusions

In this study, a vacuum magnetic field and a coil set producing that field has been derived for a quadrupolar mirror hybrid reactor with sloshing ions. The device with a 25 m long confinement region is aimed for 10 MW power, which would correspond to a steady state 1.5 GW thermal power output. The magnetic field has been optimized for MHD flute stability, low flux tube ellipticity and low field gradients, and consists of a central part based on the Straight Field Line Mirror concatenated with another field to end the mirrors. A simple recirculation and magnetic expander region has been added to the confinement region. A set of circular and quadrupolar coils has been suggested to reproduce the optimized fields with satisfactory accuracy. The vacuum magnetic field produced by the coils has then been examined for flute stability and ellipticity. The obtained magnetic field satisfies the flute stability criteria with some margin, has a maximum ellipticity of about 20 and has smooth profiles (although with some ripple) for the axisymmetric and quadrupolar field components.