Genericity for Non-Wandering Surface Flows

Abstract

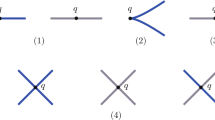
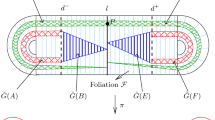
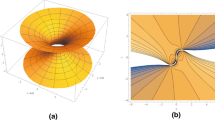
Consider the set $\chi ^{0}_{\text {nw}}$ of non-wandering continuous flows on a closed surface M. Then we show that such a flow can be approximated by a non-wandering flow v such that the complement M−Per(v) of the set of periodic points is the union of finitely many centers and finitely many homoclinic saddle connections. Using the approximation, the following are equivalent for a continuous non-wandering flow v on a closed connected surface M: (1) the non-wandering flow v is topologically stable in $\chi ^{0}_{\text {nw}}$; (2) the orbit space M/v is homeomorphic to a closed interval; (3) the closed connected surface M is not homeomorphic to a torus but consists of periodic orbits and at most two centers. Moreover, we show that a closed connected surface has a topologically stable continuous non-wandering flow in $\chi ^{0}_{\text {nw}}$ if and only if the surface is homeomorphic to either the sphere $\mathbb {S}^{2}$, the projective plane $\mathbb {P}^{2}$, or the Klein bottle $\mathbb {K}^{2}$.