Skip to main content
SpringerLink
Log in

A manually-checkable proof for the NP-hardness of 11-color pattern self-assembly tileset synthesis

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

Abstract

Patterned self-assembly tile set synthesis (pats) aims at minimizing the number of distinct DNA tile types used to self-assemble a given rectangular color pattern. For an integer k, k-pats is the subproblem of pats that restricts input patterns to those with at most k colors. We give an efficient verifier, and based on that, we establish a manually-checkable proof for the NP-hardness of 11-pats; the best previous manually-checkable proof is for 29-pats.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Notes

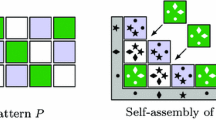
  1. In this paper, by pattern, we always mean a rectangular color pattern.

  2. Unlike the original definition in Ma and Lombardi (2008), a solution to pats is required to be directed here, but this difference does not change the problem as a minimum RTAS is always directed (Göös et al. 2014).

  3. In contrast, for example, \((\mathtt{T}, \mathtt{F}, \mathtt{T}, \mathtt{F})\) does not satisfy \(\phi \) in the sense because it satisfies more than one literal of the first clause of \(\phi \).

  4. n does not denote a negated variable. Recall that monotonicity requires that variables are never negated in clauses.

  5. Recall that m is the number of variables involved in \(\phi \).

  6. If the second choice in Lemma 2 is made, then there are only 2 tile types left uncolored at this point.

References

  • Barish R, Rothemund PWK, Winfree E (2005) Two computational primitives for algorithmic self-assembly: copying and counting. Nano Lett 5(12):2586–2592

    Article  Google Scholar 

  • Brun Y (2008) Solving NP-complete problems in the tile assembly model. Theor Comput Sci 395:31–46

    Article  MathSciNet  MATH  Google Scholar 

  • Brun Y (2008) Solving satisfiability in the tile assembly model with a constant-size tileset. J Algorithms 63(4):151–166

    Article  MathSciNet  MATH  Google Scholar 

  • Brun Y (2012) Efficient 3-SAT algorithms in the tile assembly model. Nat Comput 11:209–229

    Article  MathSciNet  MATH  Google Scholar 

  • Cook M, Rothemund PWK, Winfree E (2004) Self-assembled circuit patterns. In: Proceedings of the 9th International Workshop on DNA Based Computers (DNA 9), LNCS, vol. 2943. Springer, p 91–107

  • Culik K, Kari J (1997) On aperiodic sets of Wang tiles. Foundations of computer science potential—theory—cognition, LNCS, vol 1337. Springer, Berlin, pp 153–162

    Chapter  Google Scholar 

  • Czeizler E, Popa A (2013) Synthesizing minimal tile sets for complex patterns in the framework of patterned DNA self-assembly. Theor Comput Sci 499:23–37

    Article  MathSciNet  MATH  Google Scholar 

  • Evans CG (2014) Crystals that count! physical principles and experimental investigations of DNA tile self-assembly. Ph.D. thesis, California Institute of Technology

  • Göös M, Lempiäinen T, Czeizler E, Orponen P (2014) Search methods for tile sets in patterned DNA self-assembly. J Comput Syst Sci 80:297–319

    Article  MathSciNet  MATH  Google Scholar 

  • Johnsen A, Kao MY, Seki S (2013) Computing minimum tile sets to self-assemble patterns in 29-colors. In: Proceedings of the 24th International Symposium on Algorithms and Computation (ISAAC 2013), LNCS, vol. 8283. Springer, p 699–710

  • Kari L, Kopecki S, Étienne Meunier P, Patitz MJ, Seki S (2015a) Binary pattern tile set synthesis is NP-hard. In: Proceedings of the 42nd International Colloquium on Automata, Languages, and Programming (ICALP 2015), LNCS, vol. 9134. Springer, p 1022–1034

  • Kari L, Kopecki S, Seki S (2015b) 3-color bounded patterned self-assembly. Nat Comput 14(2):279–292

  • Ma X, Lombardi F (2008) Synthesis of tile sets for DNA self-assembly. IEEE Trans Comput-Aided Des Integr Circuits Syst 27(5):963–967

    Article  Google Scholar 

  • Ma X, Lombardi F (2009) On the computational complexity of tile set synthesis for DNA self-assembly. IEEE Trans Circuits Syst II 56(1):31–35

    Article  Google Scholar 

  • Rothemund PWK, Papadakis N, Winfree E (2004) Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biol 2(12):e424

    Article  Google Scholar 

  • Schaefer TJ (1978) The complexity of satisfiability problems. In: Proceedings of the 10th Annual ACM Symposium on Theory of Computing (STOC 1978), p 216–226

  • Seki S (2013) Combinatorial optimization in pattern assembly (extended abstract). In: Proceedings of the 12th International Conference on Unconventional Computation and Natural Computation (UCNC 2013), LNCS, vol. 7956. Springer, p 220–231

  • Stefanovic D, Turberfield A (eds) (2012) The 18th International Conference on DNA Computing and Molecular Programming, Aarhus, Denmark, 14–17 August 2012

  • Winfree E (1998) Algorithmic self-assembly of DNA. Ph.D. thesis, California Institute of Technology

  • Winfree E (2000) Algorithmic self-assembly of DNA: theoretical motivations and 2D assembly experiments. J Biomol Struct Dyn Special Issue S2:263–270

    Article  Google Scholar 

  • Winfree E, Liu F, Wenzler LA, Seeman NC (1998) Design and self-assembly of two-dimensional DNA crystals. Nature 394:539–544

    Article  Google Scholar 

  • Zhang J, Liu Y, Ke Y, Yan H (2006) Periodic square-like gold nanoparticle arrays templated by self-assembled 2D DNA nanogrids on a surface. Nano Lett 6(2):248–251

    Article  Google Scholar 

Download references

Acknowledgments

We are very thankful to the anonymous referees for their valuable comments on the earlier versions of this paper. This work is supported in part by NSF Grants CCF-1049899 and CCF-1217770 to M-Y. Kao and by HIIT Pump Priming Grant 902184/T30606, Academy of Finland, Postdoctoral Researcher Grant 13266670/T30606, JST Program to Disseminate Tenure Tracking System, MEXT, JAPAN, No. 6F36, and JSPS Grant-in-Aid for Research Activity Start-up No. 15H06212 to S. Seki.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering and Computer Science, Northwestern University, Evanston, IL, 60208, USA

    Aleck Johnsen & Ming-Yang Kao

  2. Helsinki Institute for Information Technology (HIIT) and Department of Computer Science, Aalto University, P. O. Box 15400, 00076, Aalto, Finland

    Shinnosuke Seki

  3. Department of Communication Engineering and Informatics, The University of Electro-Communications, 1-5-1, Chofugaoka, Chofu, 1828585, Tokyo, Japan

    Shinnosuke Seki

Authors
  1. Aleck Johnsen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ming-Yang Kao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shinnosuke Seki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shinnosuke Seki.

Additional information

This is an improved full version of our previous works presented at conferences Johnsen et al. (2013), Seki (2013).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Johnsen, A., Kao, MY. & Seki, S. A manually-checkable proof for the NP-hardness of 11-color pattern self-assembly tileset synthesis. J Comb Optim 33, 496–529 (2017). https://doi.org/10.1007/s10878-015-9975-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-015-9975-6

Keywords

Search

Navigation